很多初学者可能会有疑问:为什么要归一化?那么多归一化方法(BN, LN, IN, GN...)到底有什么区别?它们在处理图像、时序数据、甚至脑电波(EEG)时又有什么不同的表现?
一、研究背景 / 问题来源
想象一下,我们正在训练一个神经网络来识别猫和狗。输入模型的图片数据,其像素值范围是 [0, 255]。经过第一层卷积后,输出的特征图(Feature Map)数值可能变成了 [-500, 1000];再经过一层,可能又变成了 [-20000, 50000]。
这种现象,我们称之为 内部协变量偏移(Internal Covariate Shift, ICS)。即,在深度网络训练过程中,每一层输入数据的分布都在不断地发生剧烈变化。这会带来什么问题呢?
- 学习率难以选择:前面层的参数稍有更新,后面层的数据分布就"面目全非"。为了适应这种剧变,我们只能选择一个非常小的学习率,导致模型训练收敛得像蜗牛一样慢。
- 梯度消失/爆炸:当数据尺度过大或过小时,流经激活函数(如 Sigmoid)的梯度会变得极小或极大,导致深层网络的参数无法有效更新,这就是臭名昭著的梯度消失或爆炸问题。
- 模型泛化能力差:剧烈变化的数据分布会让模型"无所适从",更容易陷入局部最优,难以学习到数据中真正普适的特征。
归一化技术,正是为了解决这些问题而生的。它的核心目标很简单:将每一层输入的数据"拉"回一个稳定、标准的分布上(通常是均值为0,方差为1),从而让数据流动更平稳,模型训练更高效。
二、核心思想 / 原理解析
所有归一化方法,其数学本质都可以归结为一个简单的公式:
x^=x−μσ2+ϵ \hat{x} = \frac{x - \mu}{\sqrt{\sigma^2 + \epsilon}} x^=σ2+ϵ x−μ其中:
- xxx 是原始输入数据。
- μ\muμ 是这批数据的均值。
- σ2\sigma^2σ2 是这批数据的方差。
- ϵ\epsilonϵ 是一个极小的常数,为了防止分母为零。
- x^\hat{x}x^ 是归一化后的数据。
但是,简单地将数据都变成标准正态分布,可能会破坏网络学习到的特征信息。比如,某个特征的尺度本身就是其重要性的体现。因此,所有主流的归一化方法都引入了两个可学习的参数:缩放(scale)因子 γ\gammaγ 和 平移(shift)因子 β\betaβ。
最终的输出是:
yyy = γ\gammaγ ⋅\cdot⋅ x^\hat{x}x^ + β\betaβ
这样,模型就可以在训练中自己学习到最合适的分布,既享受了归一化带来的训练稳定性,又保留了数据的原始表达能力。这是一种"先标准化,再反标准化"的智慧,让网络自己决定特征的最终分布。
三、方法实现 / 模型结构
深度学习中最主流的归一化方法,其核心区别在于计算均值 μ\muμ 和方差 σ2\sigma^2σ2 的 数据范围 不同。让我们逐一解析。
假设我们的数据张量(Tensor)维度是 [N, C, H, W],分别代表 [批量大小, 通道数, 高度, 宽度]。
1. 批归一化 (Batch Normalization, BN)
BN 是归一化领域的开山之作,也是迄今为止在CNN中应用最广泛的方法。
- 归一化范围 :对 每个通道(Channel) ,在 整个批次(Batch) 内的所有样本上计算均值和方差。也就是说,它混合了来自不同样本的信息。
- 优点 :
- 极大提升了训练速度,可以使用更高的学习率。
- 起到了类似正则化的效果,有时可以替代 Dropout。
- 缺点 :
- 对 Batch Size 敏感:如果 Batch Size 太小,计算出的均值和方差就无法代表全体数据,导致模型性能急剧下降。
- 训练和推理不一致:训练时用批数据的统计量,推理时用整个训练集上累计的移动平均统计量,这增加了实现复杂性。
核心代码 (PyTorch)
python
import torch
import torch.nn as nn
# 假设我们有一个迷你的批次数据 (N=2, C=3, H=4, W=4)
# N: 批量大小, C: 通道数, H: 高度, W: 宽度
input_tensor = torch.randn(2, 3, 4, 4)
# 定义一个针对3个通道的BatchNorm2d层
# num_features 参数必须等于输入的通道数 C
bn_layer = nn.BatchNorm2d(num_features=3)
# 前向传播
output_tensor = bn_layer(input_tensor)
print("输入张量尺寸:", input_tensor.shape)
print("输出张量尺寸:", output_tensor.shape)
# 输出的每个通道在整个批次上,均值接近0,方差接近1(在可学习参数gamma, beta作用前)
# 注意:在训练模式下,BN层会更新其 running_mean 和 running_var
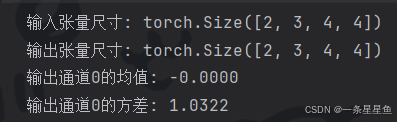
print(f"输出通道0的均值: {output_tensor[:, 0, :, :].mean():.4f}")
print(f"输出通道0的方差: {output_tensor[:, 0, :, :].var():.4f}")输出结果:
2. 层归一化 (Layer Normalization, LN)
为了解决BN对批次大小的依赖,LN应运而生,它在NLP领域的Transformer中被发扬光大。
- 归一化范围 :对 每个样本(Sample) ,在它的 所有通道(Channels) 上计算均值和方差。它完全在单个样本内部进行操作,不受其他样本影响。
- 优点 :
- 对 Batch Size 不敏感,在小批量、甚至单个样本上也能工作得很好。
- 训练和推理行为完全一致。
- 非常适合处理变长序列数据,如RNN和Transformer。
- 缺点 :
- 在CNN等图像任务上,其效果通常略逊于BN。
核心代码 (PyTorch)
python
import torch
import torch.nn as nn
# 假设我们有一个RNN的输出 (N=2, SeqLen=5, Features=10)
# N: 批量大小, SeqLen: 序列长度, Features: 特征维度
input_tensor = torch.randn(2, 5, 10)
# 定义一个LayerNorm层
# normalized_shape 参数指定要在哪些维度上进行归一化,这里是特征维度
ln_layer = nn.LayerNorm(normalized_shape=10)
# 前向传播
output_tensor = ln_layer(input_tensor)
print("输入张量尺寸:", input_tensor.shape)
print("输出张量尺寸:", output_tensor.shape)
# 输出的每个样本在特征维度上,均值接近0,方差接近1
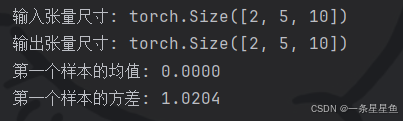
print(f"第一个样本的均值: {output_tensor[0, :, :].mean():.4f}")
print(f"第一个样本的方差: {output_tensor[0, :, :].var():.4f}")输出:
3. 实例归一化 (Instance Normalization, IN)
IN 最初是为风格迁移任务设计的,它比LN更极端。
- 归一化范围 :对 每个样本 的 每个通道 独立进行归一化。它关注的是单个样本单个通道的内部信息。
- 优点 :
- 在风格迁移等图像生成任务中效果显著,因为它能很好地保留每个样本(每张图片)的独立风格信息(对比度等)。
- 缺点 :
- 丢失了不同通道间的关联信息,不适合需要利用通道间相关性的高级语义任务。
核心代码 (PyTorch)
python
import torch
import torch.nn as nn
# 假设我们有一个批次的图像数据 (N=2, C=3, H=4, W=4)
input_tensor = torch.randn(2, 3, 4, 4)
# 定义一个InstanceNorm2d层
in_layer = nn.InstanceNorm2d(num_features=3)
# 前向传播
output_tensor = in_layer(input_tensor)
print("输入张量尺寸:", input_tensor.shape)
print("输出张量尺寸:", output_tensor.shape)
# 对第一个样本的第一个通道进行验证
sample0_ch0 = output_tensor[0, 0, :, :]
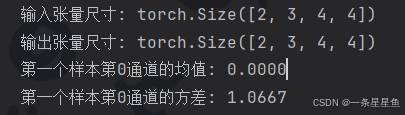
print(f"第一个样本第0通道的均值: {sample0_ch0.mean():.4f}")
print(f"第一个样本第0通道的方差: {sample0_ch0.var():.4f}")输出:
4. 组归一化 (Group Normalization, GN)
GN 是 BN 和 LN 的一种折中方案,由何恺明团队提出。
- 归一化范围 :将 通道(Channels) 分成若干个 组(Groups) ,然后对 每个样本 的 每个组 内进行归一化。
- 当 Group=1 时,GN 等价于 LN。
- 当 Group=C (通道数) 时,GN 等价于 IN。
- 优点 :
- 像LN一样,对 Batch Size 不敏感。
- 在需要利用通道间信息的任务(如目标检测、分割)上,其性能通常优于LN,且在小批量场景下远超BN。
核心代码 (PyTorch)
python
import torch
import torch.nn as nn
# 假设我们有 (N=2, C=6, H=4, W=4) 的数据
input_tensor = torch.randn(2, 6, 4, 4)
# 定义一个GroupNorm层,将6个通道分成3个组 (每组2个通道)
# num_groups: 分组数量, num_channels: 总通道数
gn_layer = nn.GroupNorm(num_groups=3, num_channels=6)
# 前向传播
output_tensor = gn_layer(input_tensor)
print("输入张量尺寸:", input_tensor.shape)
print("输出张量尺寸:", output_tensor.shape)
# 对第一个样本的第一个组 (前2个通道) 进行验证
sample0_group0 = output_tensor[0, 0:2, :, :]
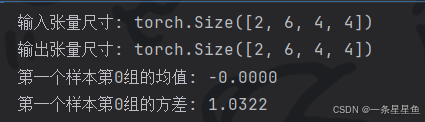
print(f"第一个样本第0组的均值: {sample0_group0.mean():.4f}")
print(f"第一个样本第0组的方差: {sample0_group0.var():.4f}")输出:
四、实验结果 / 不同数据类型的效果
归一化在不同类型的数据上,其作用和选择偏好也各有侧重。
1. 图像数据 (Image)
在图像分类、目标检测等任务中,数据通常以 [N, C, H, W] 的形式存在。
- 效果:BN 是绝对的主流和首选,尤其是在 Batch Size 较大(如 > 16)时。它能显著加速深度CNN(如 ResNet)的收敛,并提升最终精度。GN 作为小批量场景下的优秀替代品,也越来越受欢迎。
- 原因:图像的不同通道通常代表了不同的特征提取器(如边缘、纹理、色彩),BN 在整个批次上对同一特征进行归一化,符合数据 i.i.d. (独立同分布) 的假设,能够更好地估计全局的统计信息。
2. 时间序列数据 (Time Series)
对于股票价格、天气预报等时序数据,以及NLP中的文本序列,数据维度通常是 [N, SeqLen, Features]。
- 效果:LN 是这里的王者。无论是在RNN、LSTM还是Transformer中,LN都是标配。
- 原因 :
- 序列长度可变 :每个样本的
SeqLen可能不同,BN 难以处理这种动态性。 - 独立性:每个序列是一个独立的样本,将其与其他序列混合进行归一化(如BN)在逻辑上不通。LN 在单个序列的所有特征上进行归一化,恰好符合这种场景。
- 序列长度可变 :每个样本的
3. 脑电信号 (EEG Signal)
EEG 信号是一种特殊且复杂的时间序列数据,通常具有低信噪比、高个体差异的特点。
- 效果 :这里没有绝对的赢家,选择取决于具体的任务和数据预处理流程。
- LN:作为通用的序列归一化方法,依然非常适用,可以减少不同时间段或不同试验(Trial)之间的基线漂移。
- IN:如果认为每个EEG通道的信号统计特性非常独立,且需要保留通道间的相对强度关系,IN可能是一个不错的选择,可以对每个通道进行独立标准化。
- BN:如果在处理分段后的EEG数据(Epochs)时,批次较大且数据经过了良好的预处理(如基线校正),BN 也可以发挥作用,帮助模型学习到跨试验的共性特征。
总的来说,处理EEG这类信噪比低、个体差异大的生理信号时,样本内归一化(LN, IN) 通常是更稳健的选择,因为它们可以有效消除个体或单次试验的绝对尺度差异,让模型更专注于信号的模式和形态本身。
五、总结与展望
深度学习中的归一化技术,就像是搭建神经网络这座摩天大楼时的"标准化建材"。它让每一层的数据都处于一个稳定、可控的状态,从而极大地提升了整个工程的建造速度和最终质量。
我们来总结一下今天的核心要点:
| 归一化方法 | 归一化维度 | 优点 | 缺点/适用场景 |
|---|---|---|---|
| BN | [N, H, W] (对每个C) |
加速收敛,正则化效果好,CNN首选 | 依赖大Batch Size,训练/推理不一致 |
| LN | [C, H, W] (对每个N) |
不依赖Batch Size,适用于RNN/Transformer | 在CNN上效果通常不如BN |
| IN | [H, W] (对每个N, C) |
保持样本独立性,适用风格迁移 | 丢失通道间信息 |
| GN | [G, H, W] (对每个N) |
BN和LN的折中,小批量下表现优异 | 需要手动设置num_groups超参数 |
未来展望与延伸阅读:
- 自适应归一化 (AdaIN):在风格迁移和生成模型中,通过将内容特征的均值和方差对齐到风格特征的均值和方差,实现了惊艳的效果。
- 权重归一化 (Weight Normalization) 与 谱归一化 (Spectral Normalization):这些方法不对激活值(数据)动手,而是直接对网络权重进行归一化,同样能起到稳定训练的作用,尤其在GAN(生成对抗网络)中应用广泛。
- 归一化的理论分析:虽然"内部协变量偏移"是最初的动机,但后续研究表明,归一化能成功,更深层的原因可能是它平滑了损失函数的"地形",使得优化过程更加容易。
希望这篇文章能帮你彻底厘清归一化的脉络。在你的下一个项目中,不妨根据你的数据类型和模型结构,选择最合适的"归一化神功"来助你一臂之力!