STM32项目实战/PID算法学习：编码电机闭环控制实现控速+位置控制、倒立摆实现

来自嵌入式的zyz2025-10-15 15:36

理论部分

1.PID基本原理

PID简介
  • 做小车就会用到PID算法，因为小车想要走直线就要保证两个轮子PWM输出的占空比一致，不一致小车就会走不直，可是你若只考虑输出相同的占空比，但是还会存在润滑油多少等外力因素，导致两个轮子速度肯定不一样，这时候为了保证速度相同就要使用PID算法；
开环与闭环
  • 闭环相较于开环相当于多了一个反馈电路形成闭合环路，可根据反馈不断调节输出值来接近目标值，开环不会自己调节，输出一个值后就定死了，哪怕被控对象受外部因素而偏离目标值，输出值仍然不会自我调整；
  • PID叫基于误差的调节算法，就是通过反馈的实际值与目标值做差得到的误差；一般反馈的实际值都是通过传感器读取后返回MCU得到的，比如我们实现编码电机控速，就是通过编码点击上面的两个霍尔传感器得到电机此时的转速，反馈给MCU；

2.PID算法原理

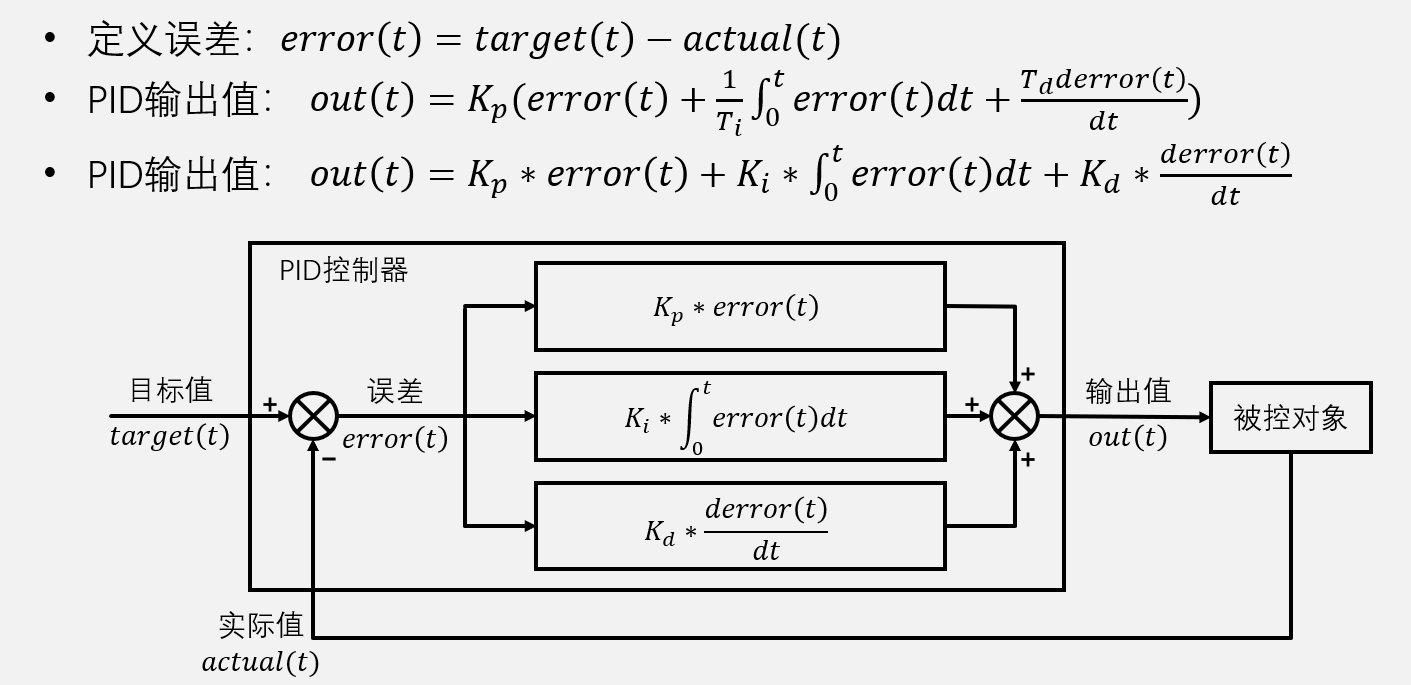
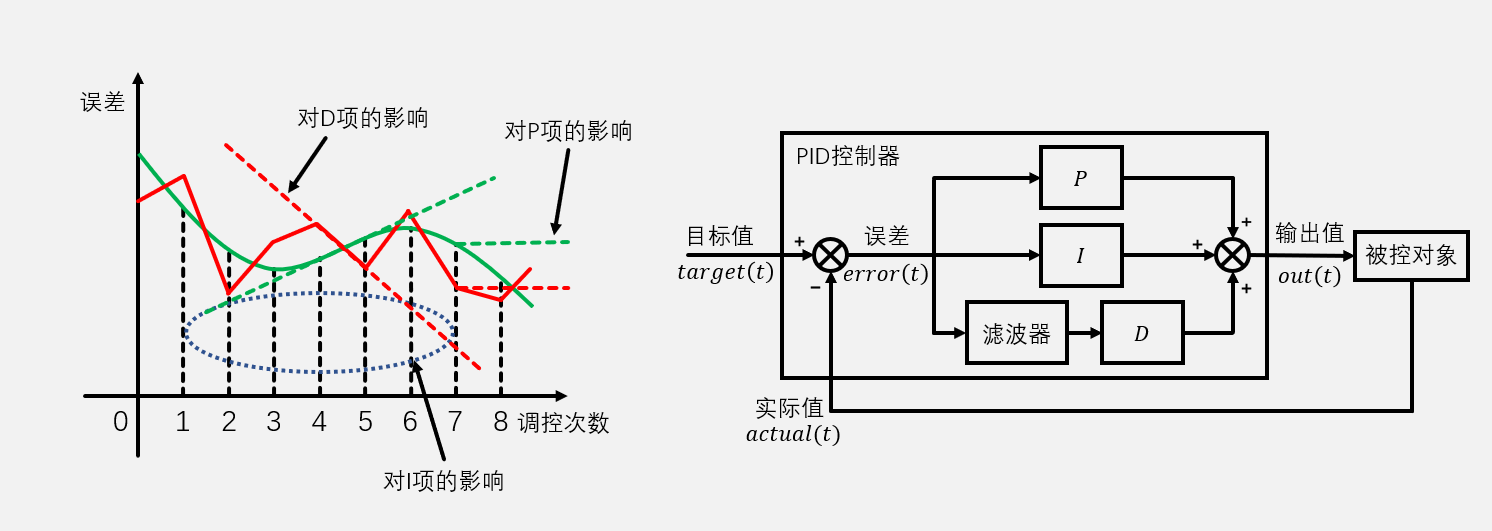
  • 看这个图就知道PID是一种基于误差调控的算法，PID的目的是让误差为0；
  • 第二个输出值公式更为常用，因为分别调节三个参数可以改变三项的值，便于调参，Kp,Ki,Kd是每一项的权重，3个参数一般都是我们直接赋值的，是PID调参需要重点调节的值；Kp对应的项称为比例项，Ki叫积分项，Kd叫微分项；（PID公式是一个经验公式）
比例项
  • Kp*error(t)就是系统调控的力度，假如error(t)=10，单位可能是速度转速等等，那么Kp给0.1的话，调控力度就是1，给1的话力度就是10，依次类推，所以Kp不能太大了，否则误差只要变化很小，比列这一项就会猛的一调，也就是超调，太小的话也不行系统响应会很慢
  • 但是不能只有比例这一项用于调节输出值，会存在稳态误差；所以Kp的取值是矛盾的，太大了超调严重，太小了稳态误差太大了，这两个问题都是我们所不能接受的；

实际例子见下图：

（差不多就是上面一条的说法验证，可以看出只靠Kp一项反馈是不行的）

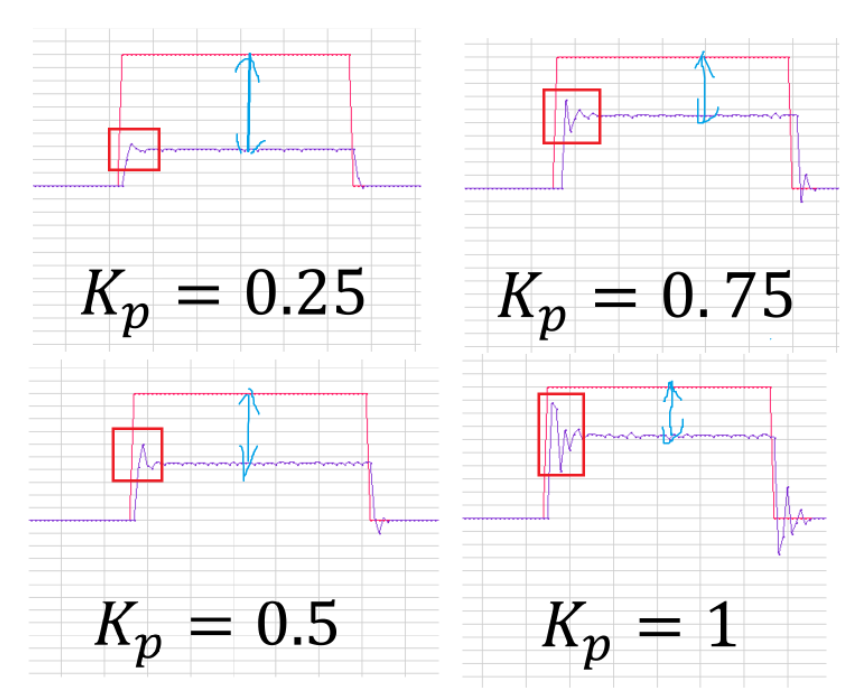
  • 红色线条表示电机目标速度，紫色线条是电机实际速度
  • 红色框框表示超调，蓝色差值表示稳态误差，稳定后的实际速度与目标速度的差值
  • 这个图就是只看P比例项的波形图，可以看到Kp越大红色框框的超调就越大
  • 按理来说只要存在误差P就会一直进行调节，那为什么会有稳态误差呢？先看看下面对稳态误差的介绍

在理想情况时不存在稳态误差，当error=0时，则实际值=目标值，不用调节嘛，因为达到稳态了；但是实际中，由于电机旋转必然存在摩擦力， PID最终目的是误差为0，但是误差为0时我们的Kp项输出也为0 ，PID的输出结果，也就是Kp计算出的out(t)直接送到了PWM的输出函数 ，也就是PWM输出为0了，电机也就没有驱动力不在转动，由于摩擦力肯定会减速， 一旦减速就会有误差，PID又要开始加速，也就是PWM输出又会增加，驱动力也会增加，直到驱动力等于摩擦力时系统达到稳态，此时速度一定没有达到目标值， 你想想在理想情况下，当电机速度小于目标值时，Kp项就会让电机加速，当电机速度大于目标值时，Kp项就会让电机减速，当电机速度等于目标值时，Kp项就会让电机匀速，此时达到稳态；那你现在有摩擦力了，相当于有一个阻碍你运动的量，你相当于Kp项消除了摩擦力，达到了稳态，实际稳态速度一定会比目标值小的

常见问题：

  • 为什么PID算法中，比例项Kp没法消除稳态误差，假设场景是电机控制速度，只有Kp控制PWM输出，实际情况是Kp与摩擦力达成稳态，没有达到目标速度，但是我觉得霍尔传感器返回测得的速度反馈给PID算法时，目标速度和实际速度误差不是还存在吗？那不是应该继续加大Kp项吗？怎么会和摩檫力达成稳态呢？
  • 上述问题有一点是典型错误，就是**"误差存在应该加大Kp项"** ,误差如果一直不变，Kp项怎么会加大了，会一直是一样的Kp给他调节；++这也就是问题所在，系统知道没有达到目标速度，但是现在他给的Kp驱动刚好抵消了摩檫力，结果速度一直不变，Kp还给这么多驱动，error(t)还是和之前一样，所以说Kp和摩檫力达成稳态了嘛。++ 系统不知道有摩擦力这么个东西，导致提供的驱动力一直达不到目标值，也没人告诉他驱动力已经和摩擦力平衡了需要继续增大驱动力，所以才需要其他项来帮助PID算法("Kp提供的驱动在理想情况下，是达到目标值的；但由于现实存在摩擦力，有一部分损耗了，所以存在稳态误差)
  • 其实这时候有人看出问题来了，Kp虽然知道有误差，但由于公式问题，被卡死在某个值；我们可以改成Kp=PWM+Kp*error，在当前速度上加Kp项，这样只要有误差直接作用在当前速度上，不就不会出现之前的情况了吗？
  • 积分项就是用于帮助消除稳态误差的**，因为比例项输出值仅取决于当前误差，与历史时刻误差无关** (这是比例项的定义，不能违反)这意味你想实现使用当前误差产生的占空比，并在此基础上加上比例项的输出作为新的占空比（这样误差为正必然加大占空比加速，为负必然减小占空比减速）是行不通的，或者说这其实是积分项的任务；
  • 能否通过不断加大Kp值消除稳态误差？
  • 首先Kp太大，会导致超调，甚至振荡；Kp提供的减小误差的PWM最终会和抵消摩檫力所需的PWM相等，达到稳态；见下图
积分项

PI控制；

  • 积分项用于消除稳态误差++。还是假设比例项的场景，现在比例项和摩檫力平衡了，但error就已存在，之前Pk驱动力只能抵消摩檫力，没法再加速了，现在有积分项了，error在积分项上不停累加，导致out(t)不断增加,直到error=0时，积分项才会停止增加；++ **积分项作用也就是提醒系统你的驱动力用来平衡摩擦力了，还得更努力增大驱动力才能达到目标值；**积分项不断累积使其控制力度越来越大，直到能够让电机占空比变大，最终达到目标值消除稳态误差
  • Ki在程序操作方法：++写积分项程序要单独定义一个变量存储历史误差，误差不断累计并求和然后乘以一个积分系数得到积分项的输出；++
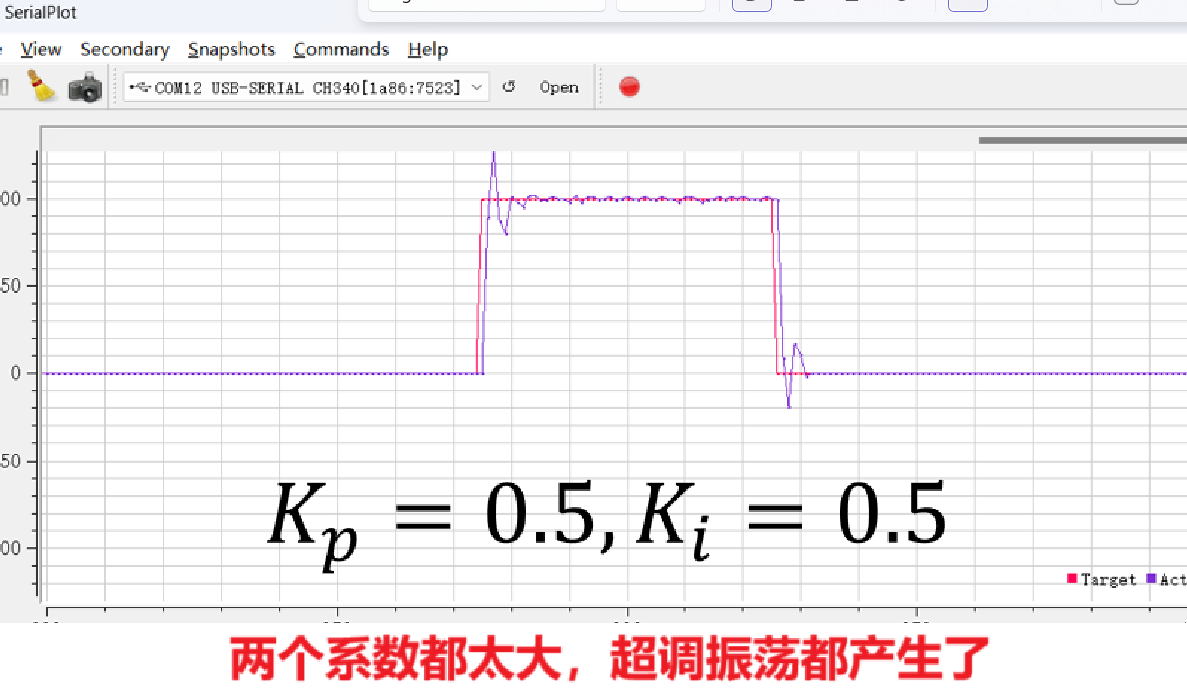
  • 积分项的弊端就是系统滞后性： 也就是当系统稳态误差消除后，此时突然要求电机反转，那么先要不断反向积分来消除之前不断累加的正向驱动力，然后再继续累计负向误差，输出反向驱动力，使其反转；这样的话，积分项的输出就太慢了。滞后性的问题不是调节慢一点，他会导致系统不稳定，出现超调现象；在一些平衡车项目里，积分项如果太大，根本不能稳定控制；积分项还有一些其他弊端，积分饱和等问题；和比例项一样，不能太大，也不能太小，否则调节又太慢了

【还有一个问题，Pi项的实现在理论和实际中是不同是，理论中Pi的累加是由积分上的t和当前的error(t)来决定的；当error(t)=0时，则Pi项为0了，只要Pi没有设置的太大，导致在前一个时刻的Pi项直接超过了目标值，就不会有超调现象发生；但代码中积分是简单累加，又是怎么样的实现方法呢？】

  • 比例项相对于积分项来说变化非常快，因为只用考虑当前时刻，你说正就是正，你说负就是负，系统响应很快；这些就是比例项的优势，所以一般积分项要配合比例项一起用，有点优势互补的意思；

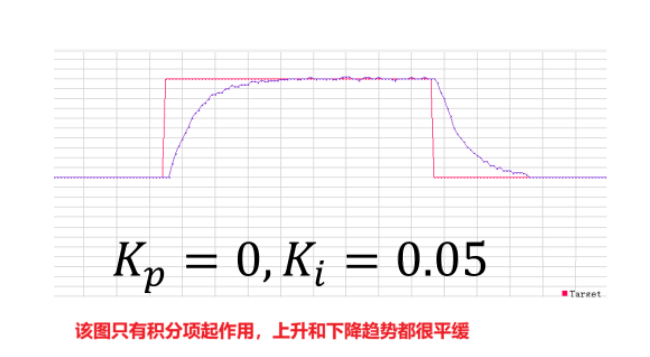
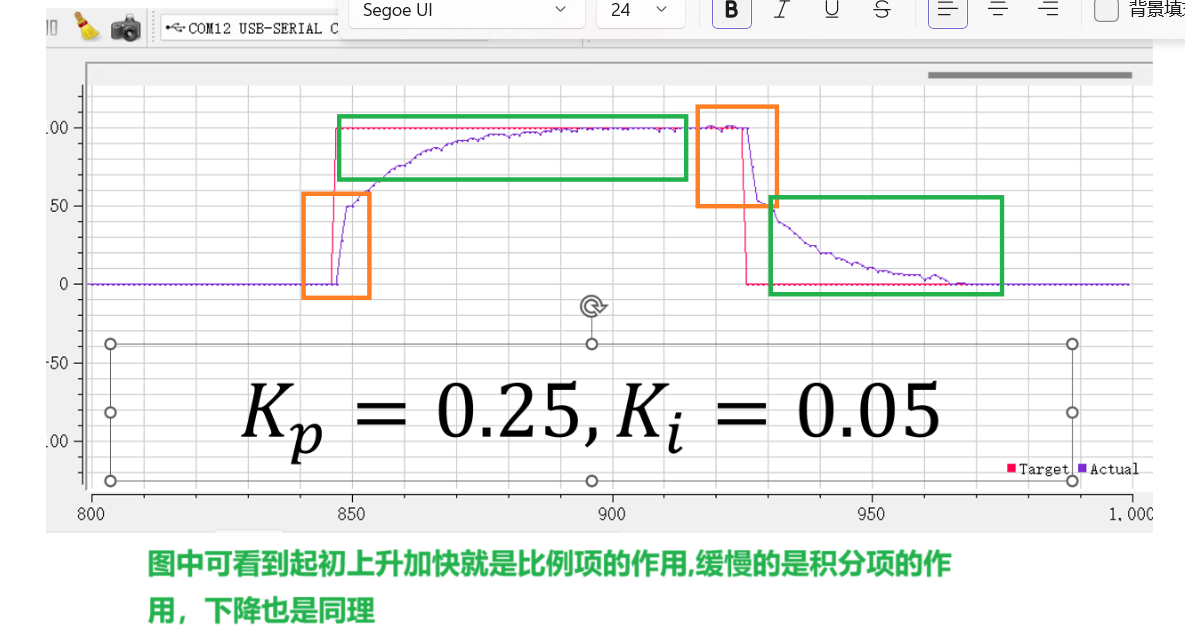
在刚开始(也就是t很小时)，只要是Kp项作用，红框部分很陡峭；到了差不多与摩檫力平衡点后，Kp才算开始发力，此时t变大，error(t)慢慢变小，缓缓接近目标值，绿框部分；由于Ki值设置的很小，当error(t)=0，并没有发生超调现象；

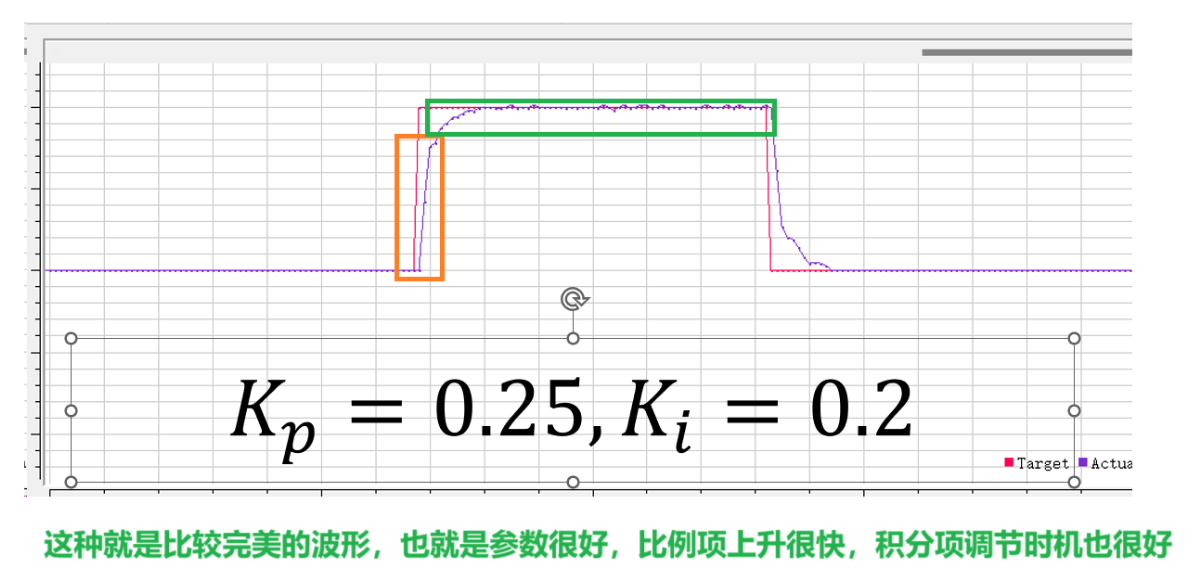
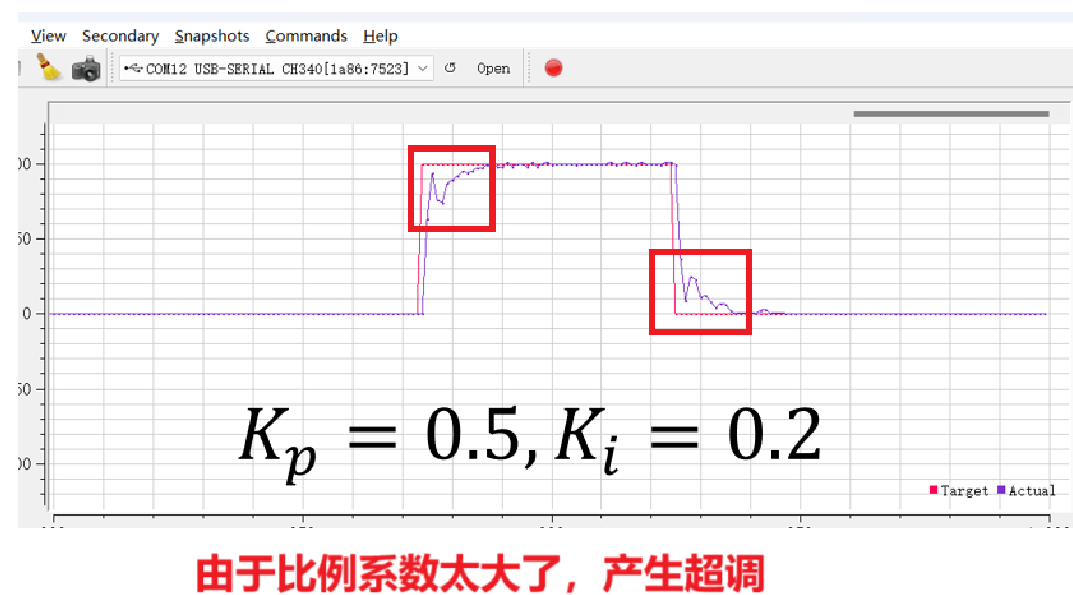
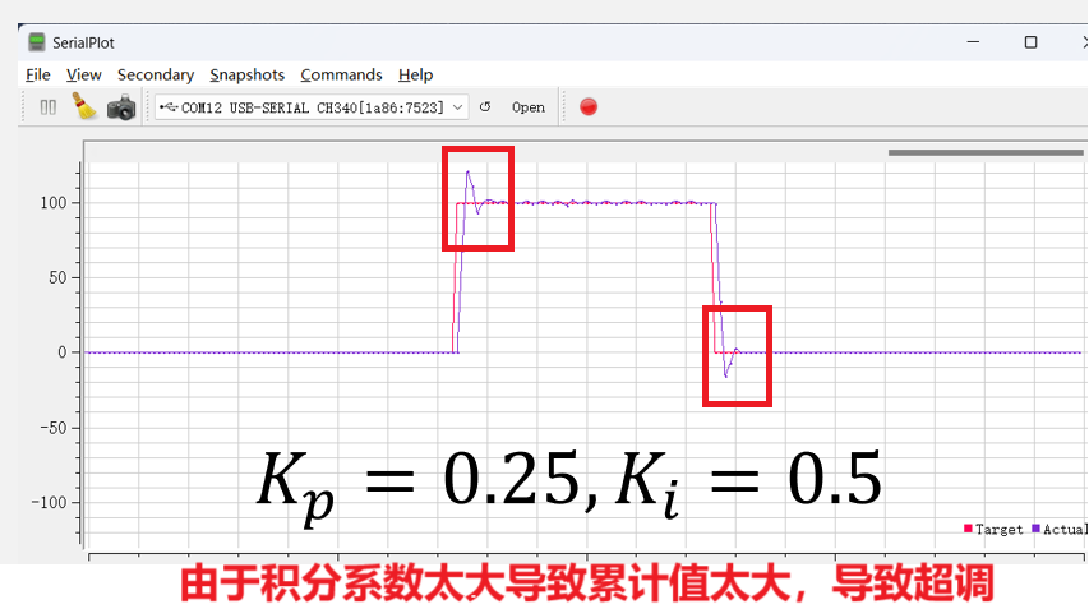
由于Ki值设置的太大了，当error(t)=0前的几次累加中，Ki项直接导致输出大幅超过目标值，这就是超调现象；

微分项

一般是PID控制器或者PD控制器；

  • Pd=Kd*当前误差变化曲线斜率；微分项不会消除误差，他就是对当前输出相反的驱动阻碍误差的急剧变化；变化速度越快/斜率越大，阻碍的力就越大；
  • 主要作用是防止超调，阻止变化过快，提前调控；在惯性较大的系统，如平衡车、倒立摆中非常重要；打个比方，++平衡车如果只有PI项很难稳定立起来，因为倒下太快了，PI来不及做出调整让重新平衡，D项的作用就是让他到下更慢一点，这是PI有更多时间调整++

【之前的P项和I项只是基于当前误差和历史误差做出调控，不会对未来进行预测/调控；对应惯性较大的系统，很可能导致超调，来回持续的振荡；而增加了Kd项后，给系统加入了阻尼，那么会使振荡不断衰减，系统会变得稳定】

为什么惯性大的系统只给PI控制会导致超调，来回持续的振荡？

  • P和I都是基于"已经发生"的误差（现在和过去）进行反应。对于惯性系统，当控制器"看到"误差减小并开始减速时(Kp和Ki输出都减小了，Kp最明显)系统巨大的动量会使其继续沿着原方向运动，导致必然的超调。
  • 而当系统超调后，误差变为负值，KI项需要一段时间才能将之前累积的正向积分"消化"掉，然后才开始累积负向积分。这个"消化"过程产生了相位滞后 。这意味着，在系统最需要反向控制力的时候，I项可能还在提供正向的控制力，从而加剧了超调。
  • 系统超调后，PI控制器"发现"负向误差太大，于是猛烈反向驱动；但由于惯性，系统很可能再次冲过目标值，产生正向超调。如此循环，系统就在目标值附近来回摆动。由于PI本身没有消耗这种摆动能量的机制，所以这个振荡会持续下去，或者需要很长时间才能平息，这就是振荡。

用开车过程来类比此时的PI控制器：

为什么增加了Kd项后，给系统加入了阻尼，那么会使振荡不断衰减，系统会变得稳定？

  • 在系统响应过程中，当实际值快速接近目标值时，误差 erroe 正在快速减小。此时，误差曲线变化率 是一个很大的负数 。D项检测到这个强烈的负变化率，它会立即计算出一个负的控制输出 （即一个制动或减速的信号）。关键点在于 ：这个制动信号是在系统尚未达到目标值、误差仍然为正 的时候发出的。它基于"照这个趋势下去，你马上就要超调了"的判断，进行了提前干预。

  • 在物理学中，阻尼是一种与运动速度成正比、方向相反的力，用于消耗系统的动能（例如汽车减震器）。D项在控制系统中扮演的正是阻尼 的角色。它的输出与系统速度（可以近似为误差变化率）成正比，并且总是反抗运动趋势 。当系统向目标加速运动时，D项产生阻力，防止它过快。当系统超调后反向运动时，D项同样产生反向的阻力，抑制其反向运动。这种始终与运动方向相反的"力"，不断地消耗系统振荡的能量。(只有PI的话，是没有这个功能的，因为他看到正向/负向距离差，就赶紧给他驱动，或者说振荡的能量本来就是他和惯性提供的)就像一个减震器，每次摆动都吸收掉一部分能量，从而使振荡的幅度一次比一次小，最终趋于稳定。

Kd的缺点：

  • 缺点就是微分系数过大时会卡顿，因为D项权重太大，给系统变化的阻尼太大了，导致PI想发生变化时,D项想让变化慢一点，阻止了PI产生的变化，导致卡顿
  • 蓝色曲线为实际值，红色为目标值，绿色为误差值（红色-蓝色），手绘的为加入合理D项后曲线
  • 上面两个中蓝线都是越接近目标值变化越快，这种就一定要加D项(++记住PI控制仿真，遇到这种曲线是一定要加D项的，可能是大惯性系统，且I过大，累计的误差多了，驱动力太大了，看下面的误差曲线，越到后面越陡；而加入D项后，D项会把曲线往下来，像手绘线那样，临近时就不会出现超调了)++
  • 下面两个图也能看出来误差变化太快需要D项帮助

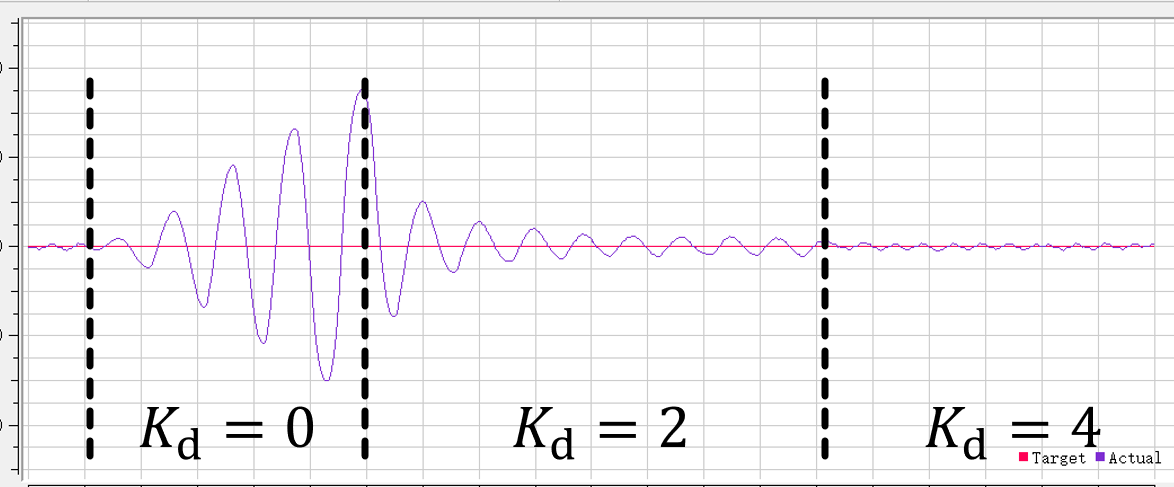
这就很明显了，第一个图中只有PI作用，那么每当有误差时，PI的调节就会超调导致误差更大，越调越超调，离目标值越来越远，但是加上D项之后就发现会离目标值越来越近，而且微分系数越大阻尼越大，阻尼振荡越来越小；

【一般对于电机的定速控制用PI控制就行了，这个系统一般不会来回震荡；而对于电机/倒立摆的定位置控制，可以用PD控制器，因为定位置控制一般稳态误差很小，而且比较容易超调、来回振荡；如果发现有一点稳态误差，可以加一点点I项，但不能加大，否则会导致定位置控制恒不稳定】

3.离散PID&程序实现思路

连续和离散形式PID
  • 连续PID需要用模拟电路实现，不断进行计算和调控；离散PID则是设置一个调控周期T，MCU每隔T时间，进行一次PID计算和调控；在单片机中，PID是间隔进行的；
  • k表示是第几次调控；error(k)是第几次调控时当前的误差直；T是离散后的调控周期；Pi项是把第k次调控之前的所有error累加起来的值；
  • 第三个公式中**，将我们设置的调控周期T融入了Ki和Kd中，千万别忘了这点；当我们改变T时，如果用的是第三个公式，Ki和Kd也要对应修改才行；用第二种形式就不需要；**

对离散形式PID的理解:

  • **比例项：**这里的k表示第k次调控，P项也就是比例系数乘以第k次的调控时刻的误差
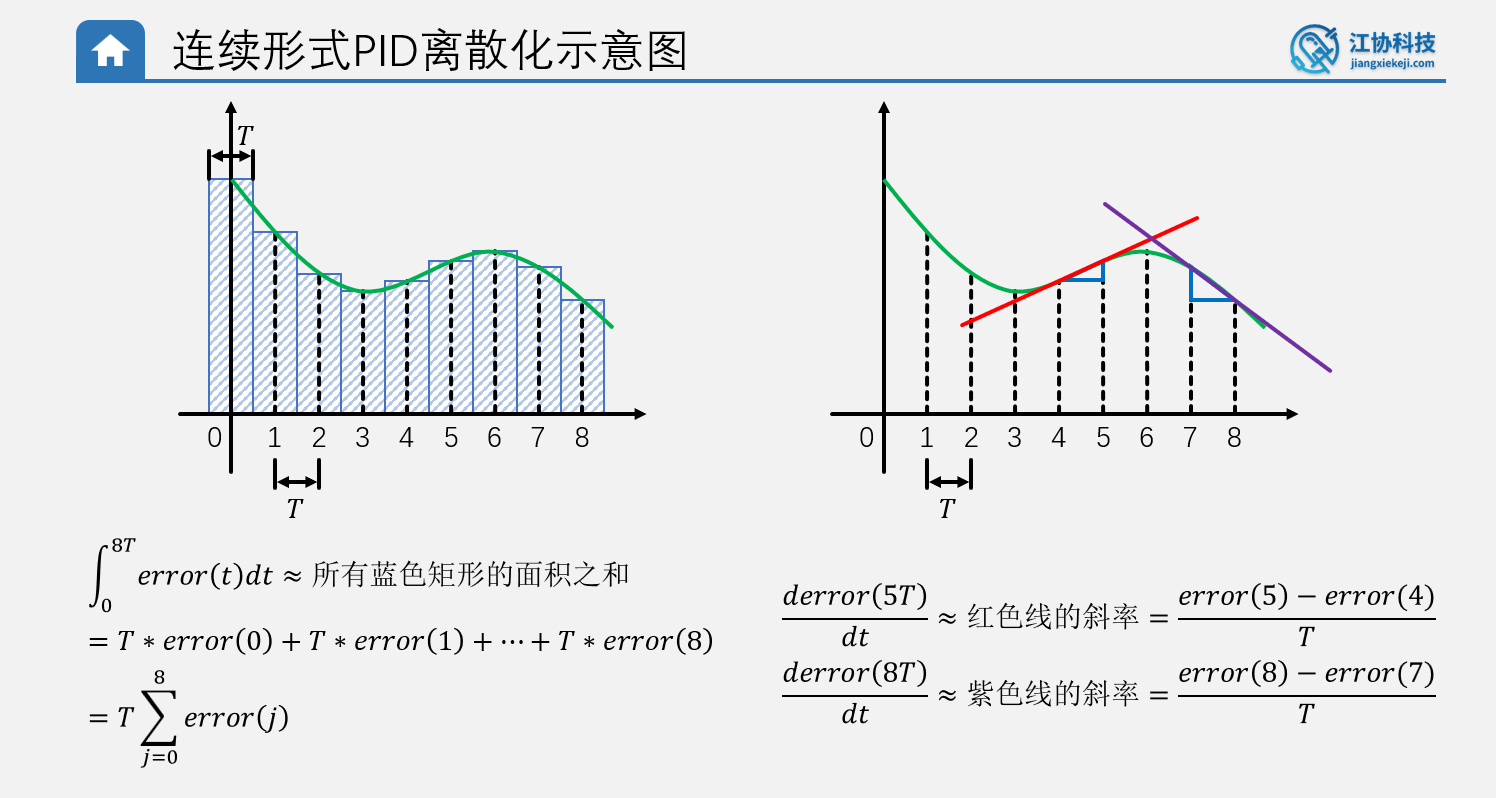
  • **积分项：**看下面这个图就是连续和离散化的区别，第一个图就是积分的定义，其实就是蓝色矩形面积之和，T就是宽（T越小求和越准确），error(j)就是长，乘积就是面积，j是一个临时变量用于使用循环求和
  • **微分项：**某一点的微分就是斜率，这里也是使用两点来计算斜率，T也是越小计算结果越精准
位置式PID和增量式PID
  • 位置式PID就是之前推的离散形式PID，能够应用于各种场景，速度控制、温度控制、位置控制、状态控制等等都可以；
  • 增量式PID其实就是相邻两次PID之间的差值；增量式PID就是本次、上次、上上次三次erroe的线性组合，没有累加和乘除；所以当我们使用增量式PID只需要记录三次error的值就行了；
  • **两者的区别：**位置式可直接给被控对象，增量式需要被控对象有积分功能，也就是需要被控对象拥有记录上一次状态的功能，才能在此基础上根据增量改变

【在控制理论中，积分（Integration） 的本质就是 累加（Summation） 。在位置式PID里，积分项 Ki * ∑e(j) 是在控制器内部完成的，控制器自己累加误差，然后输出一个全量，被控对象直接执行就行了，被控对象不需要知道上一个时刻的量；

在增量式PID里，控制器把积分的任务 "外包" 给了被控对象。控制器只负责计算"该变化多少"： Δu(k)被控对象需要执行： 当前实际状态 = 上一时刻状态 + Δu(k)

这个 当前状态 = 上一状态 + 增量 的物理过程，就是一个完美的积分器。 被控对象必须拥有这个功能，增量式控制才能生效。常见的步进电机是有这个功能的，内部有一个位置计数器，永远记录着电机当前的位置；但是像一个普通阀门上述没有这种功能的，使用增量式PID要注意】

两者直接皆可以实现相互转化：

  • 位置式PID代码中，把上一次PID值存起来，用本次PID值-上次PID值=增量；但没必要，因为可以直接用增量式，位置式的计算要比增量式复杂的多。
  • 对应第三条的解释，可以在增量式PID代码中定义一个变量out，每次计算得到增量后，执行out+=out增量，将增量累加到out变量上；此时这个out就是全量输出，这时候被控对象就没什么限制了**(这种增量式PID我们叫做内部积分的增量式PID)**

对第四条的解释：

  • 位置式PID中间变量是误差积分(Pi项)，可以单独进行积分限幅，防止积分饱和；而内部积分**(就上一点的增量式PID实现全量输出讲解，没有内部积分就是只输出out增量的增量式PID)**的增量式PID，没法/不用单独对积分环节限幅；就是说内部积分的增量式PID，只要对输出值限幅，就可以同时实现积分限幅和输出限幅两个功能了；而位置式PID中，输出限幅和积分限幅必须分开进行；
  • 位置式PID输出的得到的是全量输出值，如果有噪声干扰，不同输出值相差会很大，导致执行机构大幅度变化；增量式PID则可以单独对输出值增量进行限幅，防止执行机构大幅度变化
  • 增量式PID适合自动控制和手动控制切换的场景，自动控制也就是使用PID，手动控制也就是不使用PID，当你将三个参数全部给0时就是自动控制，这个时候如果是位置式电机会由于参数为0输出值也立马变为0，点击停转，但是增量式具有存储上一个输出量的功能，输出值可以位置在当前值所以不会停，这个时候就可以手动调节输出值
PID程序实现

第一步：首先确定周期T的值，每隔T时间，程序执行一次PID调控；**调控周期T一般取决于被控对象的快慢。**例如倒立摆、四轴飞行器、平衡车等，这些对象变化的很快，比如你给1S，早就倒了，一般给20/10/5/1ms就差不多了，对这些快变化的对象来说，调控越快，对象就会越稳定；但也不能无限制快， 太快硬件传感器分辨率受限,，比如姿态传感器每隔5ms才更新数据，你设置1ms没意义。对应电机控速来说，T不需要太大，20-100ms都差不多；电机控制调控也不能太快，因为受到编码器分辨率限制，调控周期越快，编码器测速分辨率就越低，太快，编码器测得的速度数据不准确

**T需要实践经验来反复调节尝试，不能太快也不能太慢，太慢起不到平衡作用，太快硬件传感器分辨率受限,**以下是三种实现每隔时间T实现一次PID调控的方法

不准确，且会阻塞主程序运行；

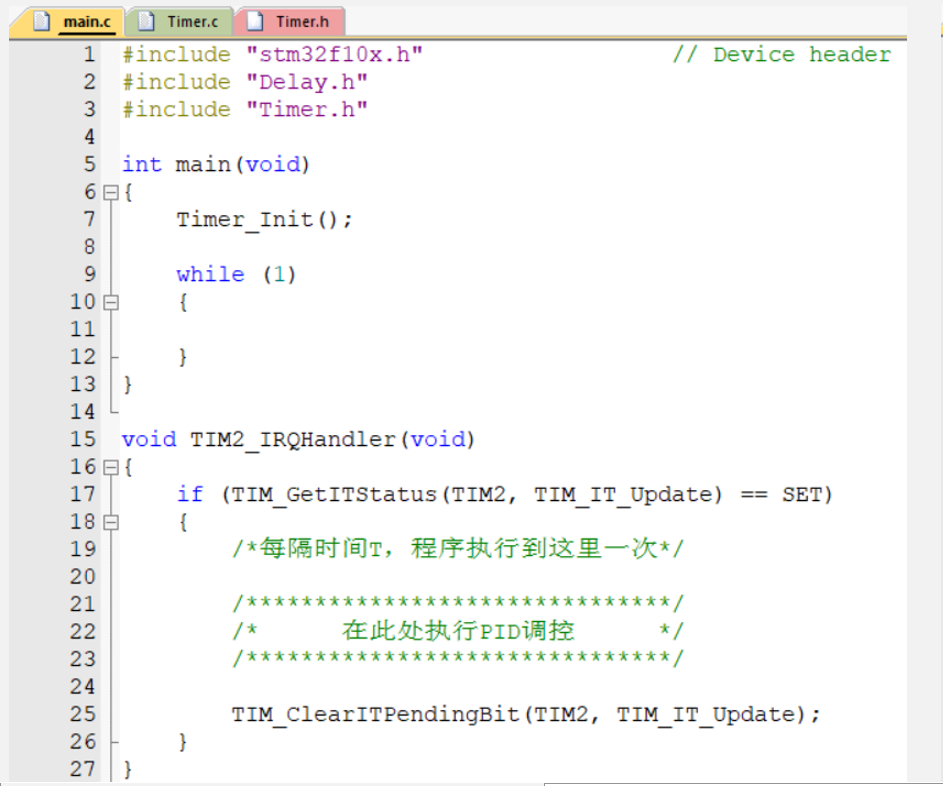
定时中断。每隔一段时间进行定时中断，PID过程就在中断函数里进行；这样做时间准确，不干扰主程序，有利于程序多个功能互不干扰地运行；这个方法使用最多也是最推荐的；

弊端：涉及硬件操作的函数(常见就是读取引脚的传感器函数)，不能既在中断又在主程序中调用；中断和主程序是多线程(就是互不干扰，互不了解)多线程操作同一硬件，，会导致资源访问冲突；

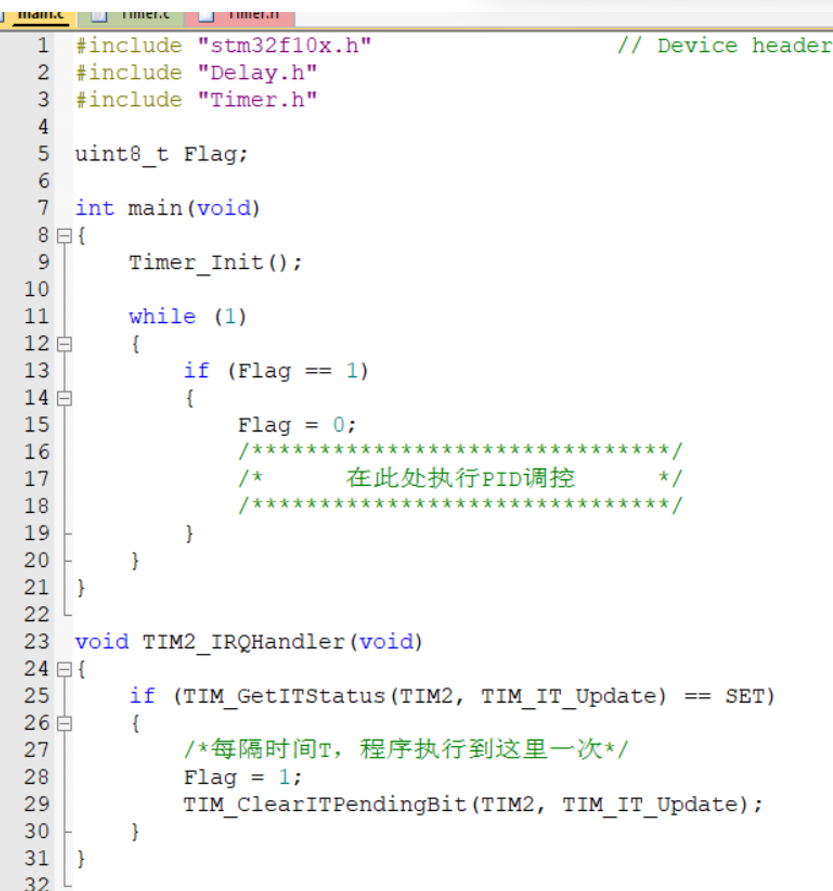
第一个方法最简单但是阻塞式弊端太多；第二个方法定时中断一般最常用，但是要注意不能在中断和主函数里操作同一个硬件，避免资源访问冲突； 第三种也是定时中断，但是自定义标志位可以在主函数里执行PID调控，该方法主程序一定不能阻塞了
位置式PID程序的实现思路

**注意：**PID实现过程中，变量可能会出现负数、小数，所以变量类型必须用float;

  • 输出限幅是因为怕PID的输出值超过了硬件的接受范围，所以设置一个接受的上下限

增量式PID程序的实现思路

  • 这里是控制器内积分得到out而不是out的增量

额外补充

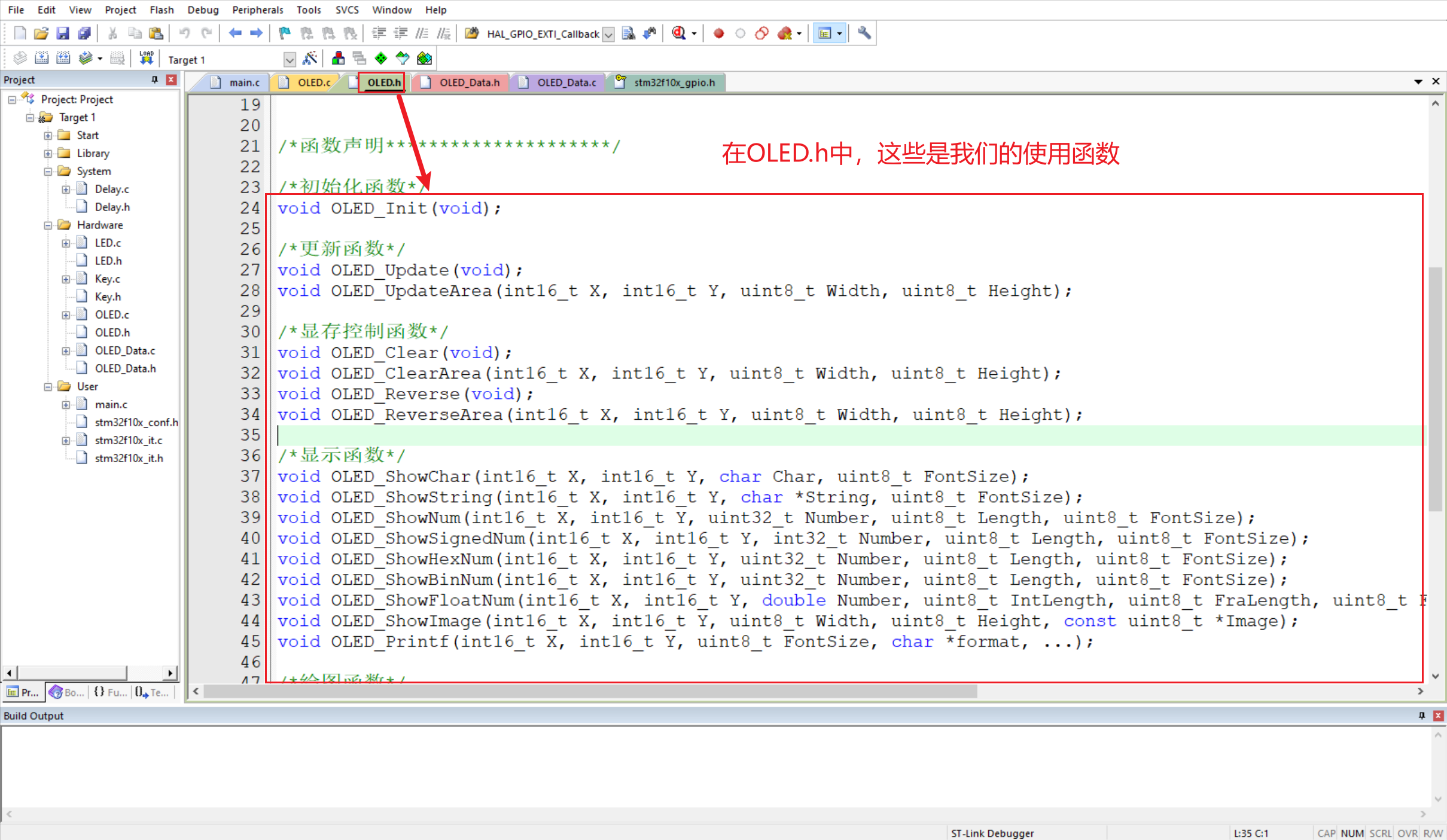
1.OLED.h函数及操作解释
css 复制代码 
/*函数声明*********************/
 
/*初始化函数*/
void OLED_Init(void); // OLED初始化，主函数调用
 
/*更新函数*/
void OLED_Update(void); // 更新OLED全部区域
void OLED_UpdateArea(int16_t X, int16_t Y, uint8_t Width, uint8_t Height); // 更新指定区域
 
/*显存控制函数*/
void OLED_Clear(void); // OLED清屏
void OLED_ClearArea(int16_t X, int16_t Y, uint8_t Width, uint8_t Height); // 清除指定区域
void OLED_Reverse(void); // OLED反色
void OLED_ReverseArea(int16_t X, int16_t Y, uint8_t Width, uint8_t Height); //指定区域反色
 
/*显示函数*/
void OLED_ShowChar(int16_t X, int16_t Y, char Char, uint8_t FontSize); // 显示字符
void OLED_ShowString(int16_t X, int16_t Y, char *String, uint8_t FontSize); // 显示字符串（包括中文）
void OLED_ShowNum(int16_t X, int16_t Y, uint32_t Number, uint8_t Length, uint8_t FontSize); // 显示数字
void OLED_ShowSignedNum(int16_t X, int16_t Y, int32_t Number, uint8_t Length, uint8_t FontSize); // 显示有符号数字
void OLED_ShowHexNum(int16_t X, int16_t Y, uint32_t Number, uint8_t Length, uint8_t FontSize); // 显示16进制数字
void OLED_ShowBinNum(int16_t X, int16_t Y, uint32_t Number, uint8_t Length, uint8_t FontSize); // 显示二进制数字
void OLED_ShowFloatNum(int16_t X, int16_t Y, double Number, uint8_t IntLength, uint8_t FraLength, uint8_t FontSize); // 显示浮点数
void OLED_ShowImage(int16_t X, int16_t Y, uint8_t Width, uint8_t Height, const uint8_t *Image); // 显示图像
void OLED_Printf(int16_t X, int16_t Y, uint8_t FontSize, char *format, ...); // 打印格式化字符串
 
/*绘图函数*/
void OLED_DrawPoint(int16_t X, int16_t Y); // 画一个点
uint8_t OLED_GetPoint(int16_t X, int16_t Y); // 读取指定位置的点
void OLED_DrawLine(int16_t X0, int16_t Y0, int16_t X1, int16_t Y1); // 画直线
void OLED_DrawRectangle(int16_t X, int16_t Y, uint8_t Width, uint8_t Height, uint8_t IsFilled); // 画矩形
void OLED_DrawTriangle(int16_t X0, int16_t Y0, int16_t X1, int16_t Y1, int16_t X2, int16_t Y2, uint8_t IsFilled); // 画三角形
void OLED_DrawCircle(int16_t X, int16_t Y, uint8_t Radius, uint8_t IsFilled); // 画圆
void OLED_DrawEllipse(int16_t X, int16_t Y, uint8_t A, uint8_t B, uint8_t IsFilled); // 画椭圆
void OLED_DrawArc(int16_t X, int16_t Y, uint8_t Radius, int16_t StartAngle, int16_t EndAngle, uint8_t IsFilled);
 
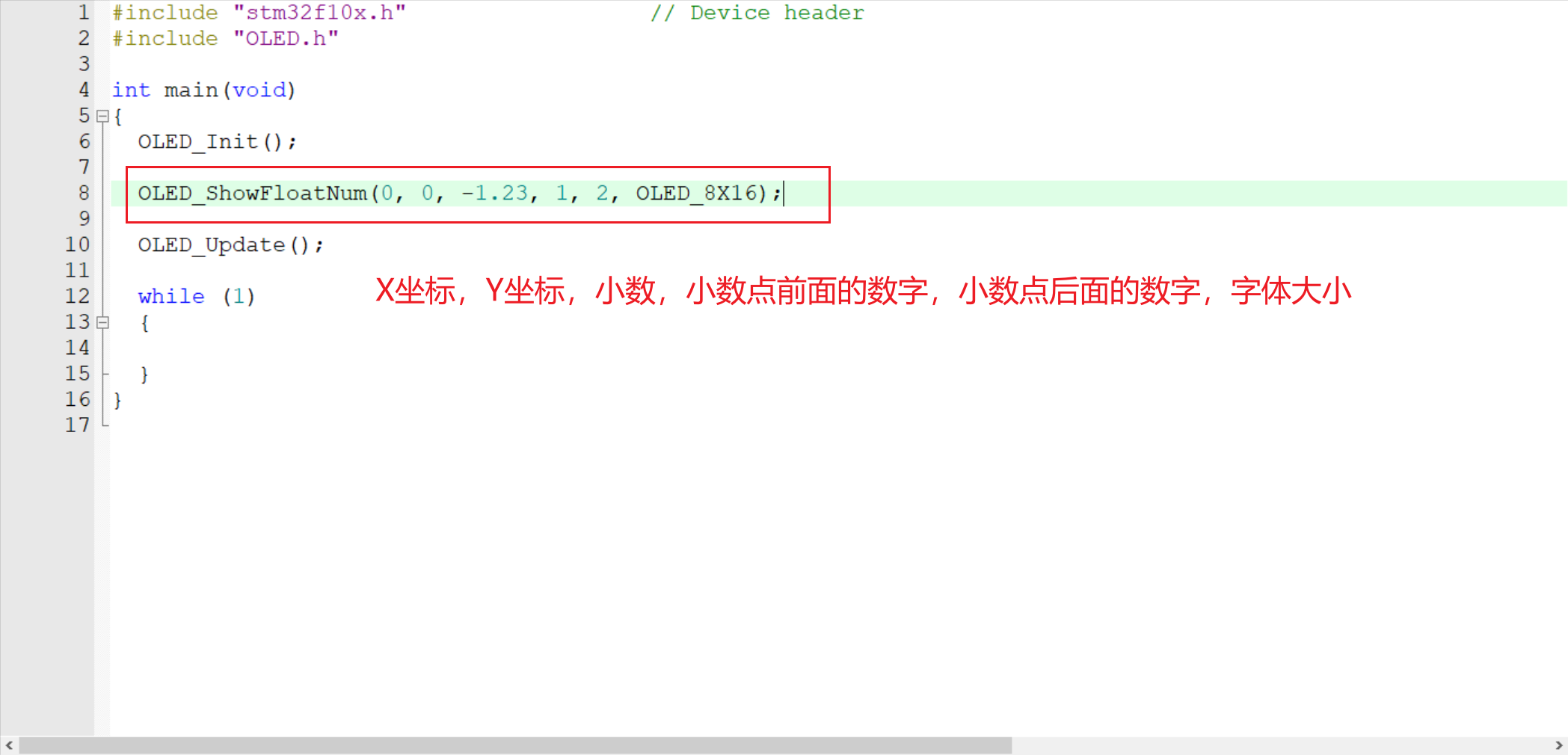
/*********************函数声明*/

函数的使用（以浮点数为例）:

每次写完都要加上OLED_Update()；才行；

中文取模：

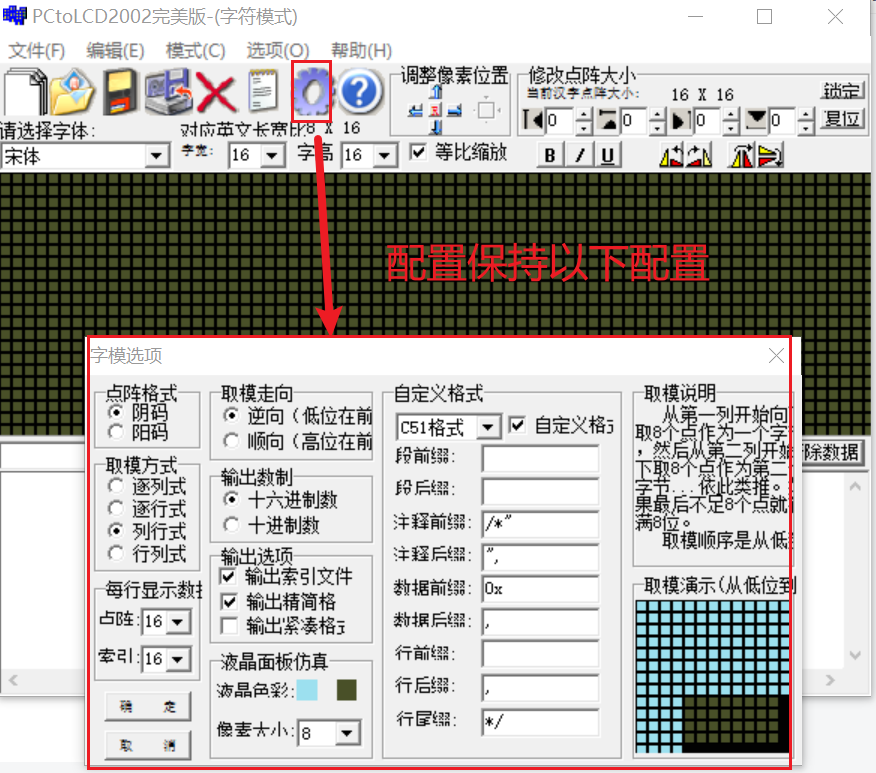
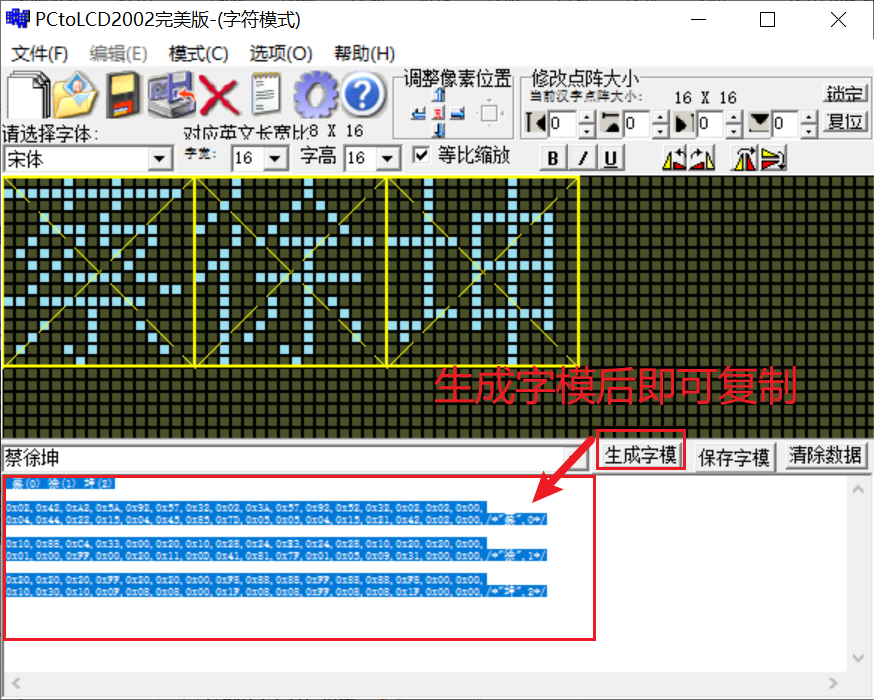
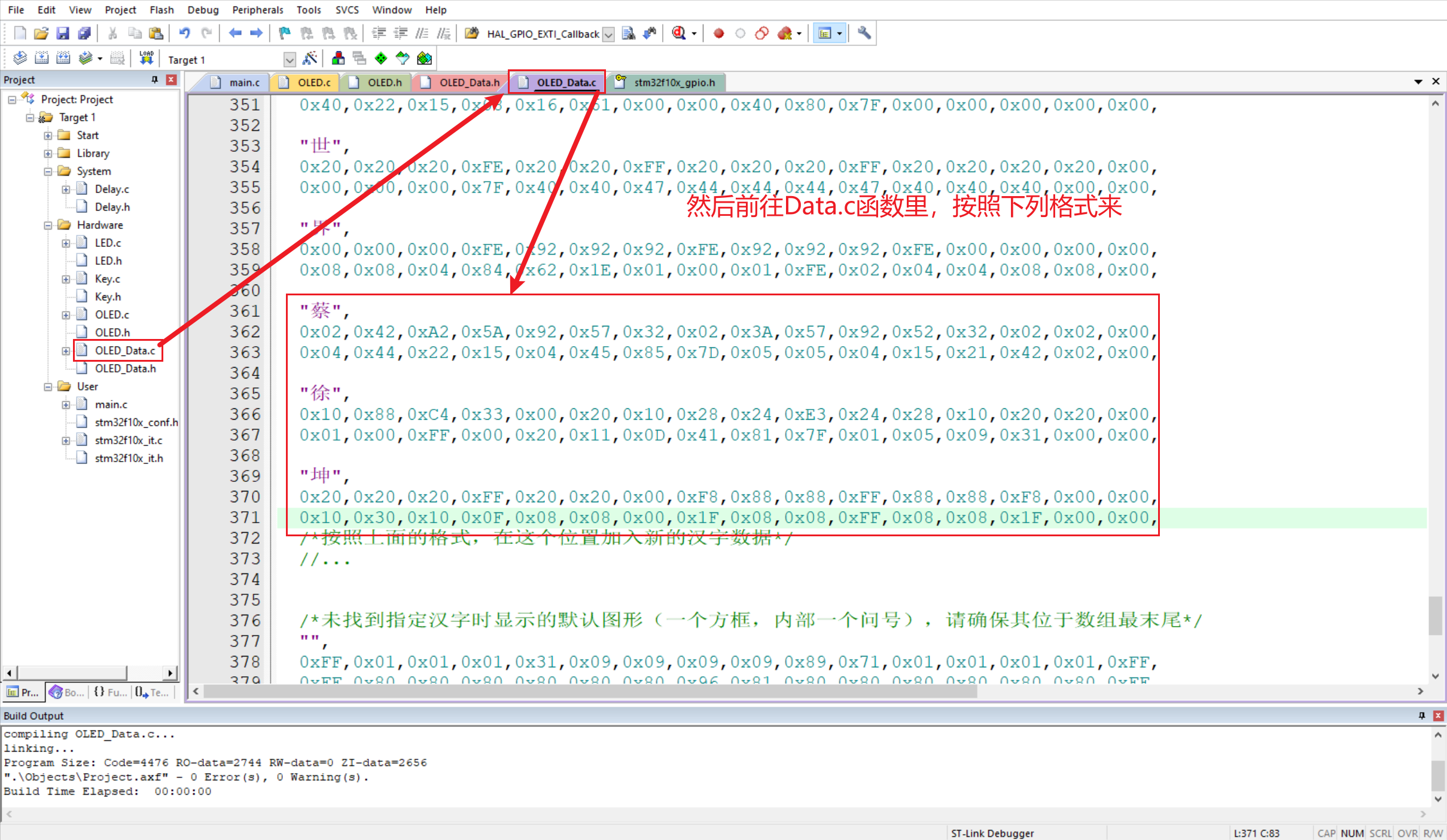
显示图像:

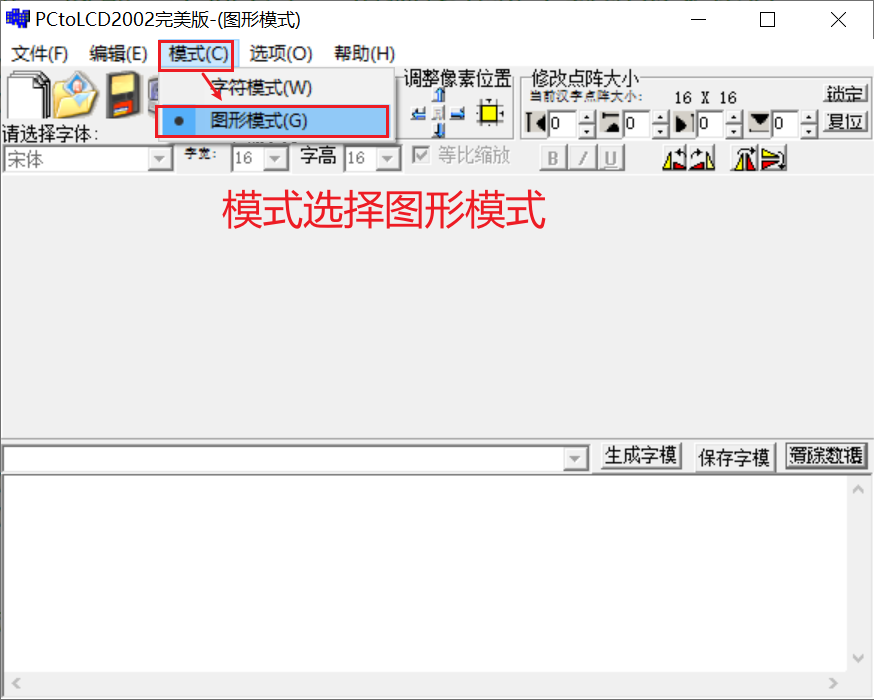
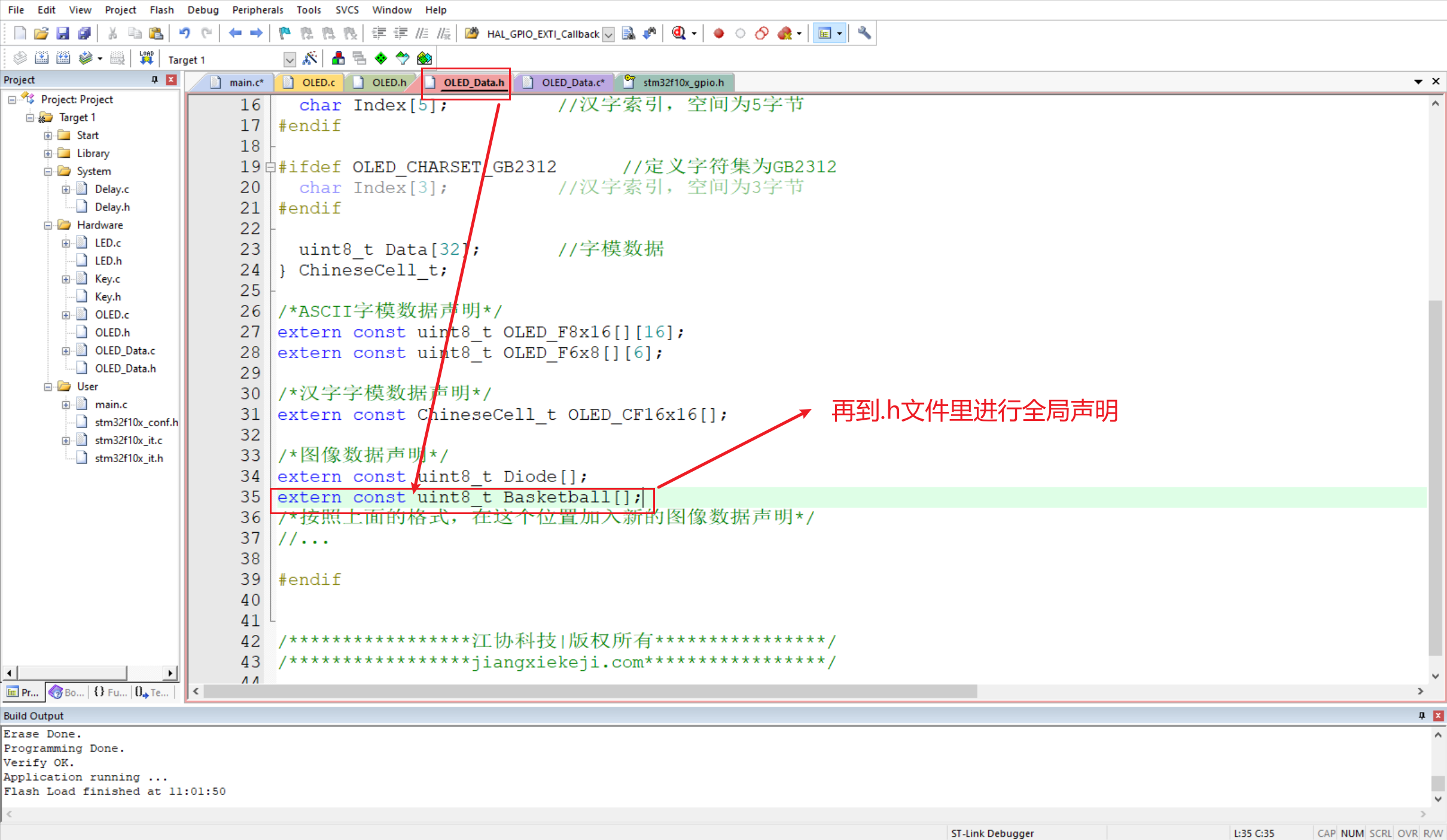
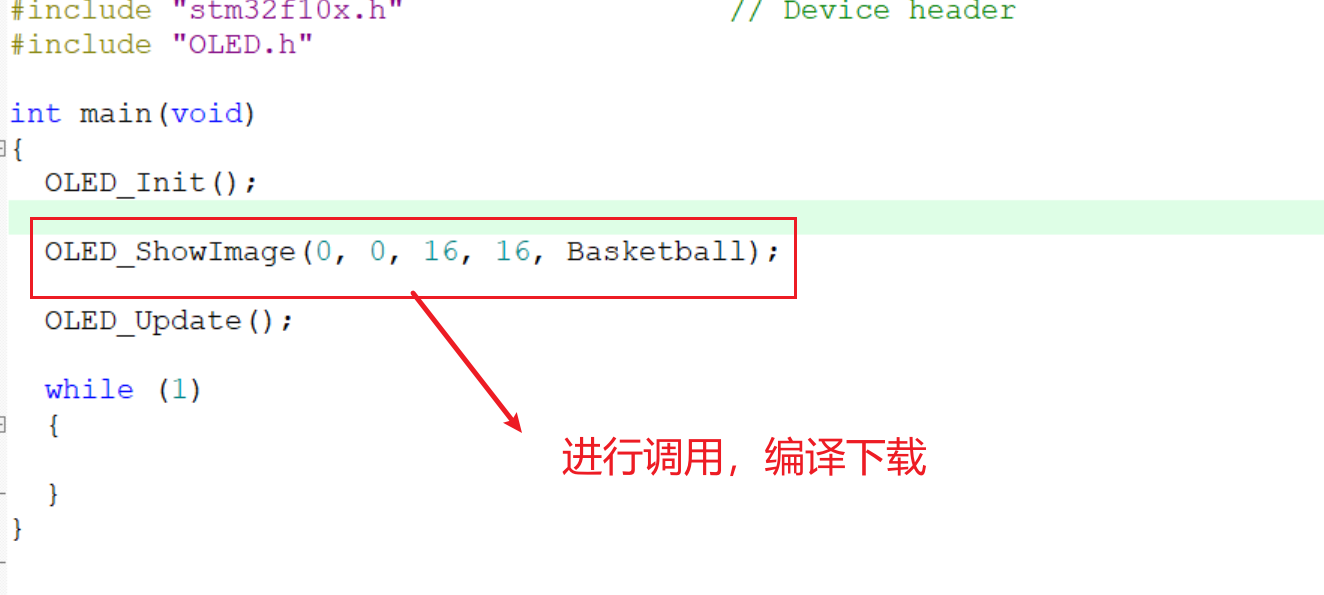
2.编码电机原理讲解
3.非阻塞式按键原理及代码实现

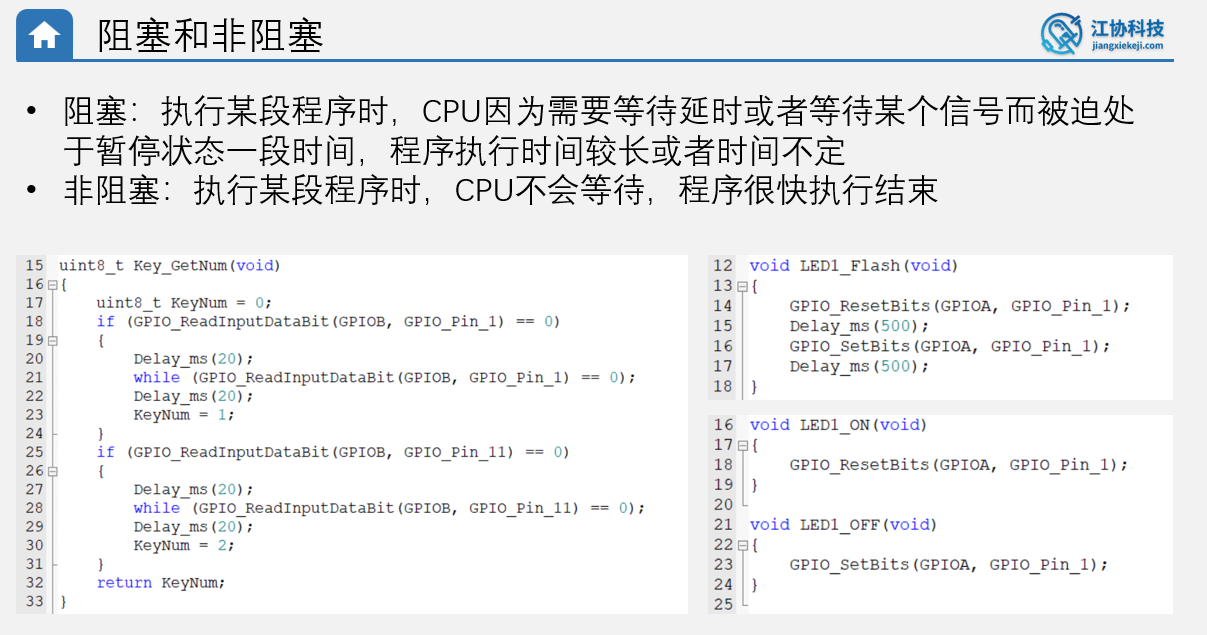
由于普通Delay延时函数会出现阻塞主函数的运行，会发生主函数变慢或者停止的情况；像左图，如果我们一直按住按键不松手，程序就一直阻塞，无法执行其他程序；右上图有两个延时函数，他们会阻塞主程序运行500ms，在500ms内如果有什么信号，我们就会超过；这些就是阻塞；

而右下角，两个函数就是非阻塞式程序，他们运行时间不会超过1ms，并且不会妨碍中断这些敏感的程序；

简单来说，阻塞和非阻塞主要区别就是**程序执行时间，**这种我们只使用裸机程序+定时器，再配合一些程序思维也可以解决这些问题；

STM32江科大学习笔记，全功能按键非阻塞式实现，按键点击，双击，长按 - 详解 - wzzkaifa - 博客园

4.常见优化算法方法

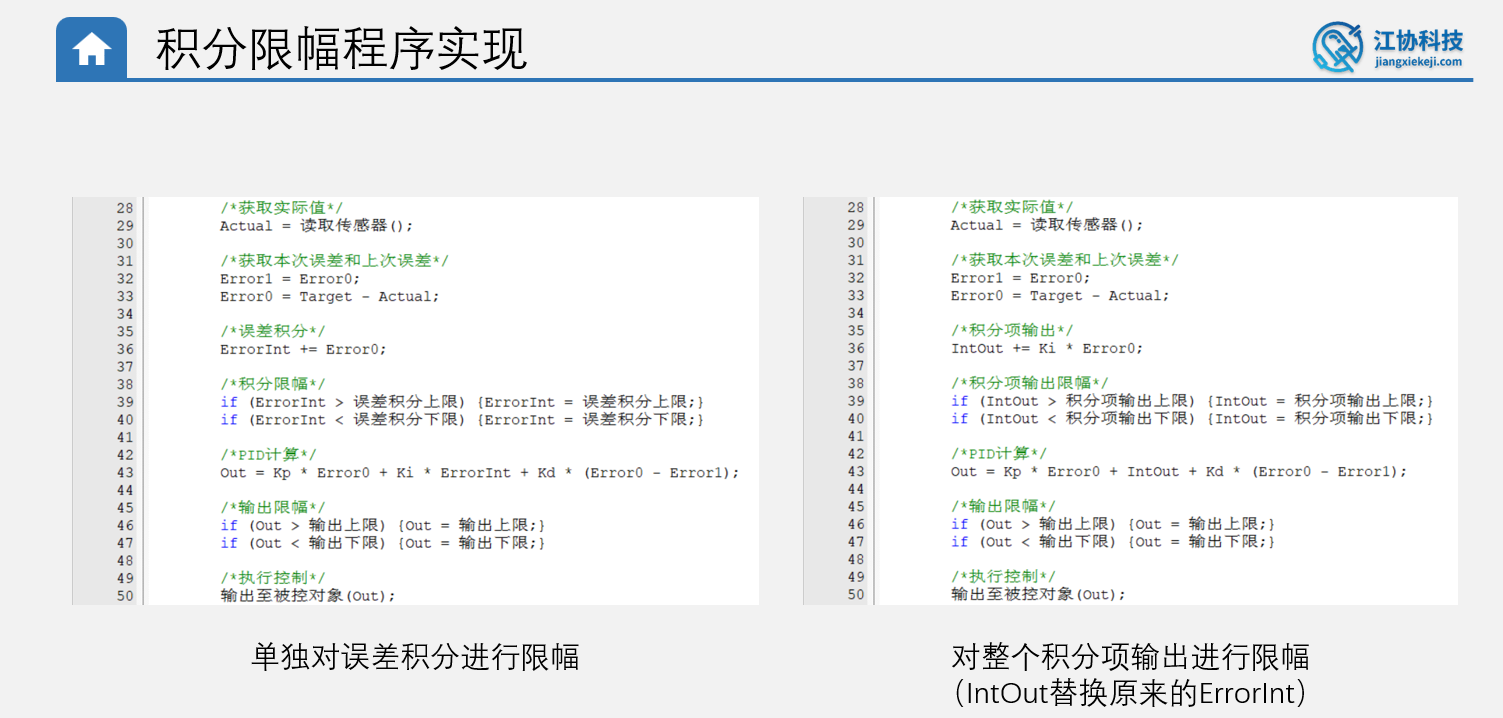
积分限幅（只用于位置式）
  • **造成原因：**断电或者电机卡死等原因会使电机的实际速度为0，和目标值相差过大，导致积分项会一直无限制积分，而此时一旦又通电，由于积分项太大了电机会满速运转，直到积分项反向积分使电机转速实际值与目标值重合，此时改变目标值才会有效果，在此之前无论如何修改目标值都没用。电机通电满速运转一段时间且无法控制是危险的
  • **实现思路：**限制误差积分的增大上限，也就是哪电机停转了，也不能让积分项一直增大，而是增大到一定值就停止增大
  • **阈值设置：**最大阈值也就是让积分项=最大输出值，此时误差积分=最大out值/Ki
积分分离（定位置）
  • 常见的都是定速使用PI，定位置用于PD就够了，当定位置使用PD时会发现实际值与目标值总会有那么一点点误差无法消除，是因为理论上只要有PWM电机就会动，但是实际上有摩擦力，PWM很小时驱动力只能够平衡摩擦力，推不动电机旋转，导致一点点的稳态误差，我们也知道积分项可以用来消除稳态误差，实际上确实可以，但是用于定位置控制时又会出现更大的问题------超调，而且这个超调微分项不能解决
  • 使用积分项的超调原因：理论上定位置不存在稳态误差，因为摩擦力基本可以忽略不计，我们只使用比例项完全就够用了，因为定位置最后OUT输出值也为0，电机不旋转，也就是比例项的输出值刚好就是整个OUT输出值（OUTp=OUT），此时加上积分项后，就会是OUTp+OUTi>OUT，这就会导致超调，实际图像就是下图所示，会先超过目标值，然后此时比例项迅速反应并进行反向积分，积分项会迅速反向积分，当积分项正向积分与反向积分抵消时，此时比例项才会使误差为0

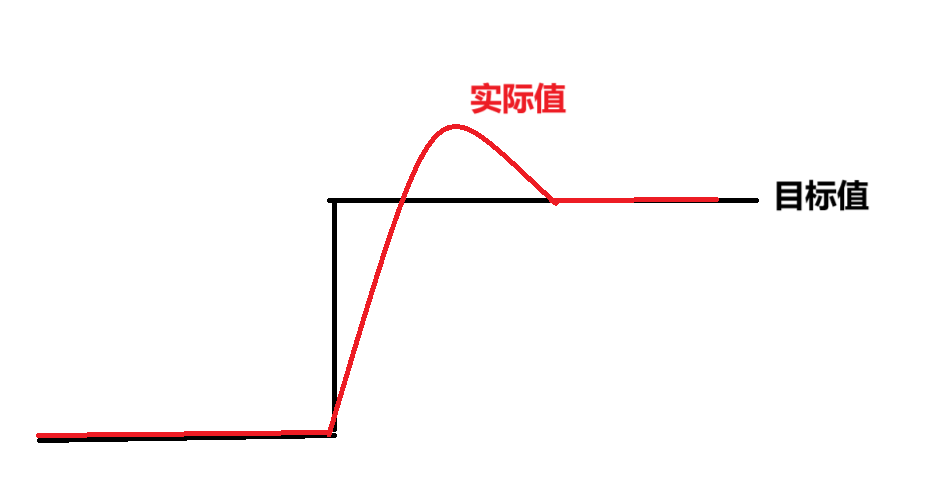
解决方法：当误差大时使用PD，误差很小时使用PID，防止积分项一直积分导致驱动力不可避免的过大导致超调，如果只在后半段接近目标值才积分，积分时间很短，积分项很小不会产生过大驱动力导致超调

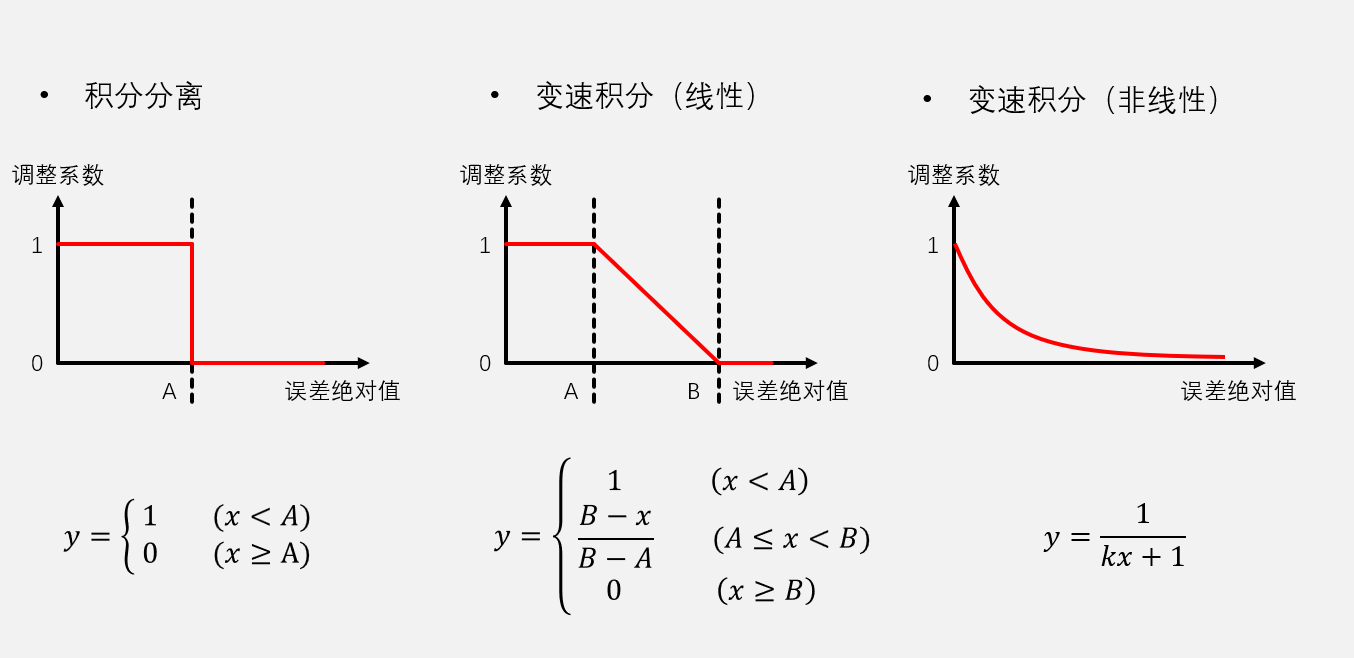
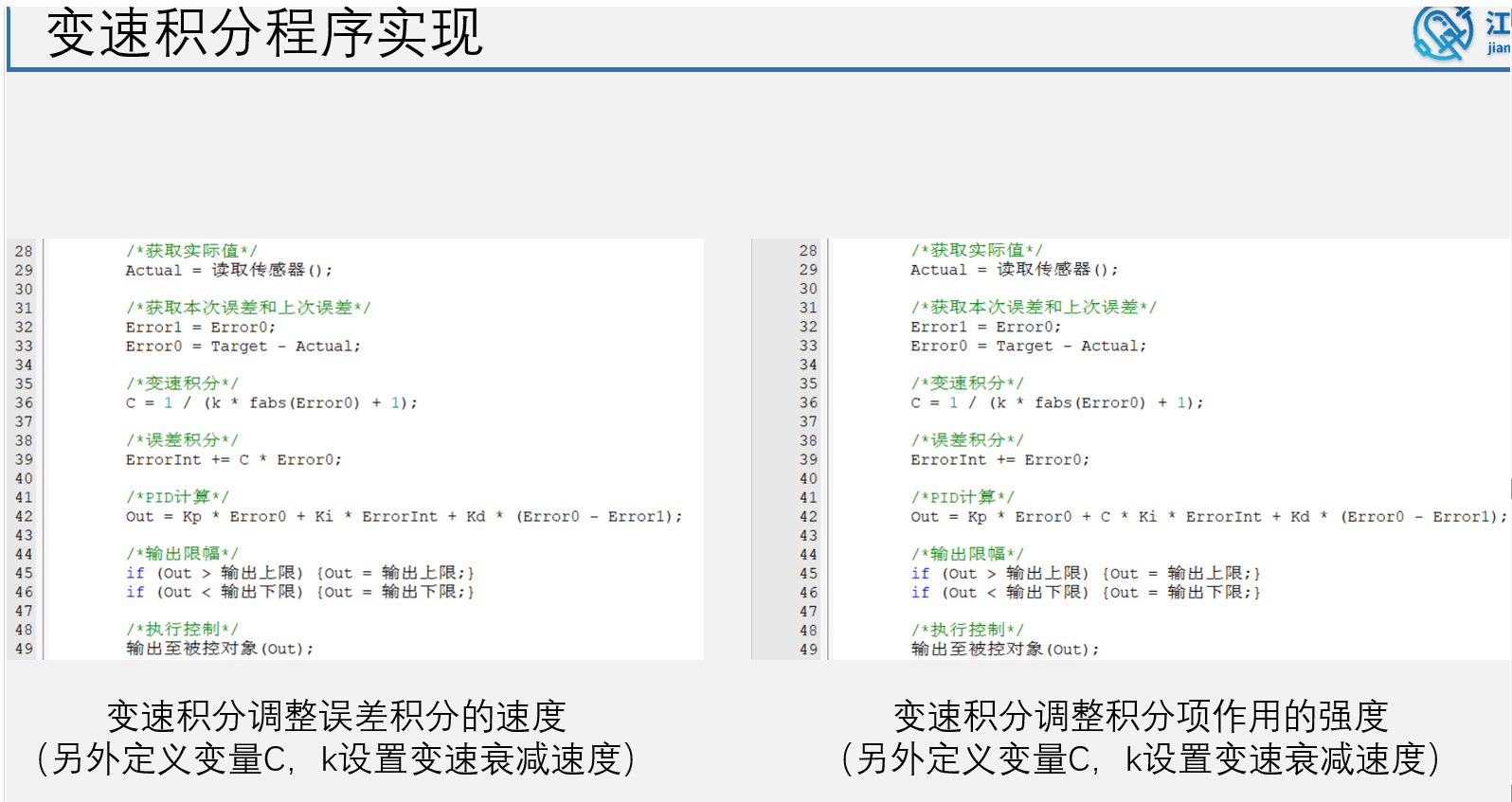
变速积分

变速积分其实就是积分分离的升级版，积分分离是只存在有积分项和无积分项两种情况，变速积分则是积分项大小会随误差大小变化而变化，麻烦的是需要设置一个函数表示变化关系，如果函数不好的话，效果甚至不如积分分离

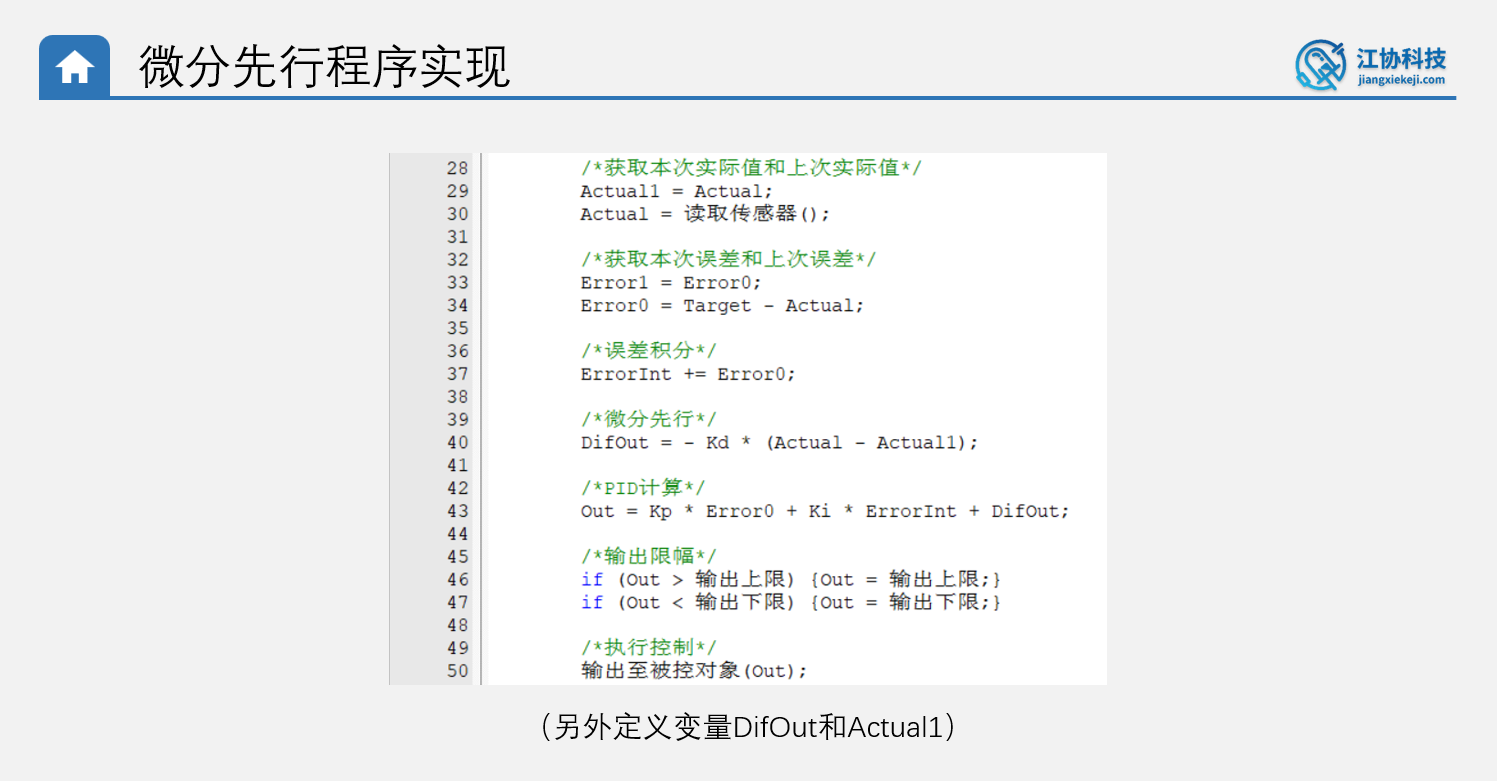
微分先行
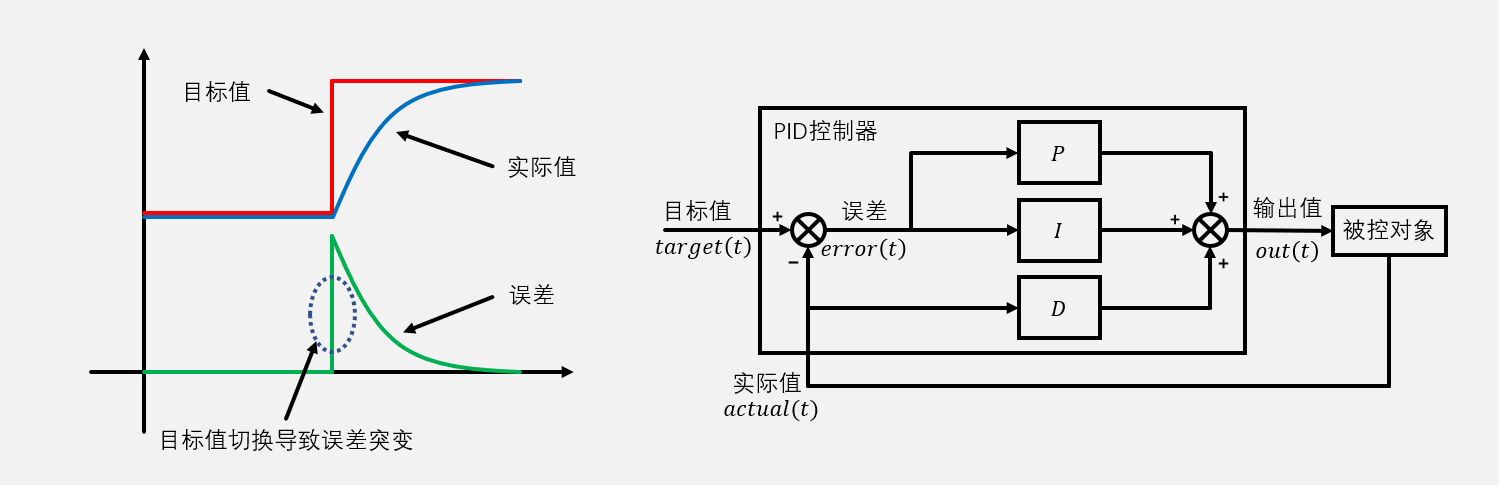
  • 当目标值突然变化时，微分项是误差的斜率，也就是起初微分项接近正无穷大，后面误差变化正常，斜率是负的反向微分而且微分项会越来越小
  • 目标值频繁切换导致数据产生尖峰，且Kd越大尖峰越高，按理来说只存在微分项时，只改变目标值电机不会旋转，因为微分项只起到给实际值添加阻尼效果，应该不具备输出能力，但是实际上纯微分项控制时电机会由于误差快速变化导致旋转，那么其实可以只对实际值进行微分，无论误差如何变化，此时微分项就只起到加阻尼效果而不具备输出能力，而且实际值也不会突变。在计算误差进行PI之前提前对实际值进行微分，这就是微分先行的原理
  • 但是实际情况要看使不使用微分先行，因为微分项可以帮助比例项更快响应目标值变化，尤其是误差较大的变化，如果只需要微分项起到阻尼效果可以加微分先行
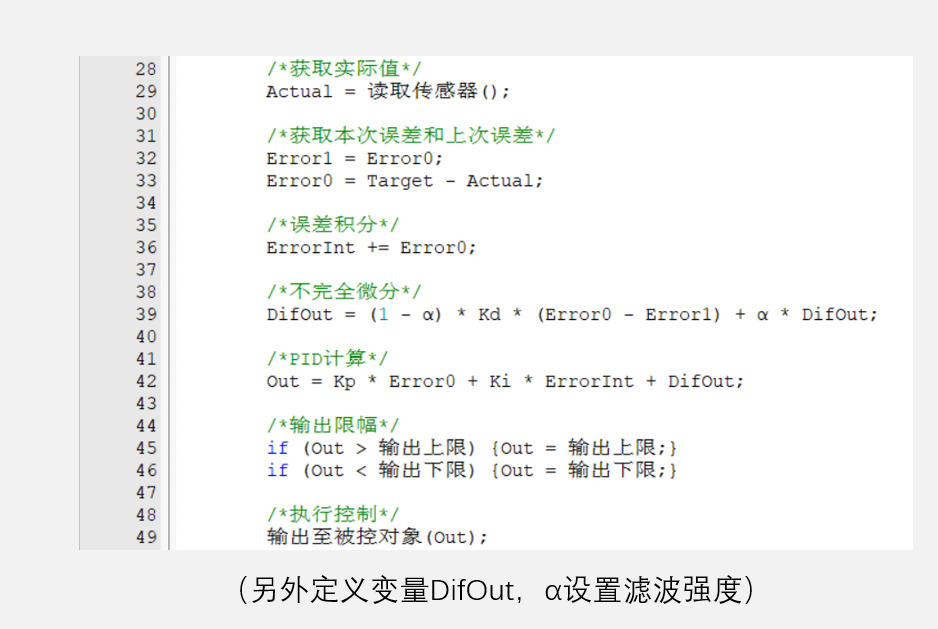
不完全微分
  • 观察上面的图，红色曲线代表噪声，绿色曲线是理想值，噪声对比例项来说影响很小，就是噪声和理想值的误差值之差，一般噪声和理想值不会相差很大；对积分项来说就是曲线下的面积，噪声有时候比理想值高有时候也有低的时候，所以实际面积两者相差不大；微分项代表斜率，看图可知理想值的斜率为正的时候，噪声可能直接为负值了，这个影响就很大，所以需要过滤噪声也就是添加滤波器，也就是不完全微分
  • 之所以不对开始的值全部滤波，是因为滤波会增加时延，导致PID响应速度变慢
  • 不完全微分的微分项就是本次微分项和上次微分项占不同权重然后加起来得到新的微分项，a取0.5相当于均值滤波，a越大本次微分项权重越低，滤波效果就越好
  • 一阶惯性单元滤波公式：假设输入是x(k),输出是y(k),则有y(k)=(1-a)x(k)+ay(k-1),意思是本次输出为本次输入和上次输出的加权平均值
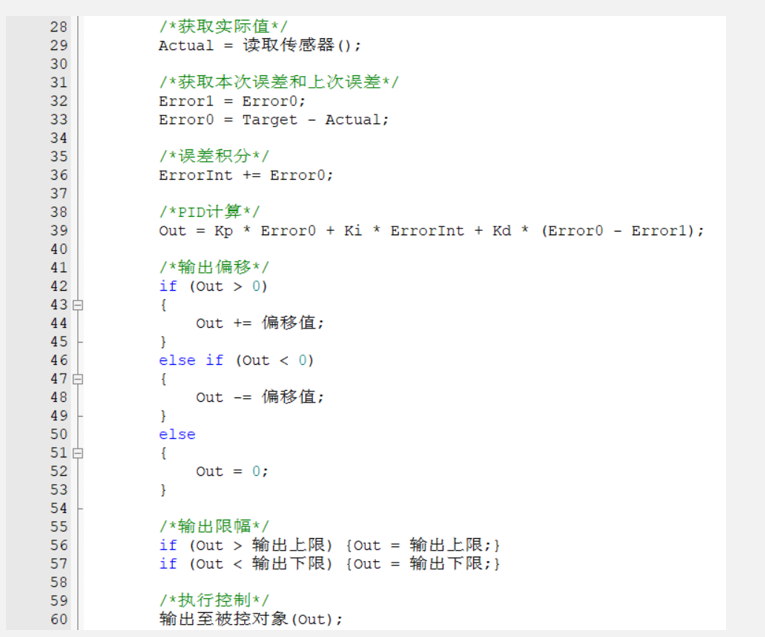
输出偏移
  • 也就是PWM要么就不输出，一旦输出，该PWM就一定要能驱动电机
  • 偏移量需要单独写一个测试程序测量
  • 缺点就是很难稳定，因为PID但凡调控电机必定转动，目标值与实际值会一直存在误差很难为0，甚至目标值都在抖动有噪声，所以就会一直抖动
输入死区
  • 死区阈值
注意事项
  • 积分限幅一般都要使用
  • 微分项可以帮助比例项更快响应目标值变化，尤其是误差较大的变化，如果只需要微分项起到阻尼效果可以加微分先行
  • 输出偏移+输入死区可以将误差控制在可接受范围，但是积分分离可以无误差，但是会有积分项的滞后性
  • 滤波有延时性，滤波效果越好延时一般越严重

5.双环PID基本原理

串级PID简介
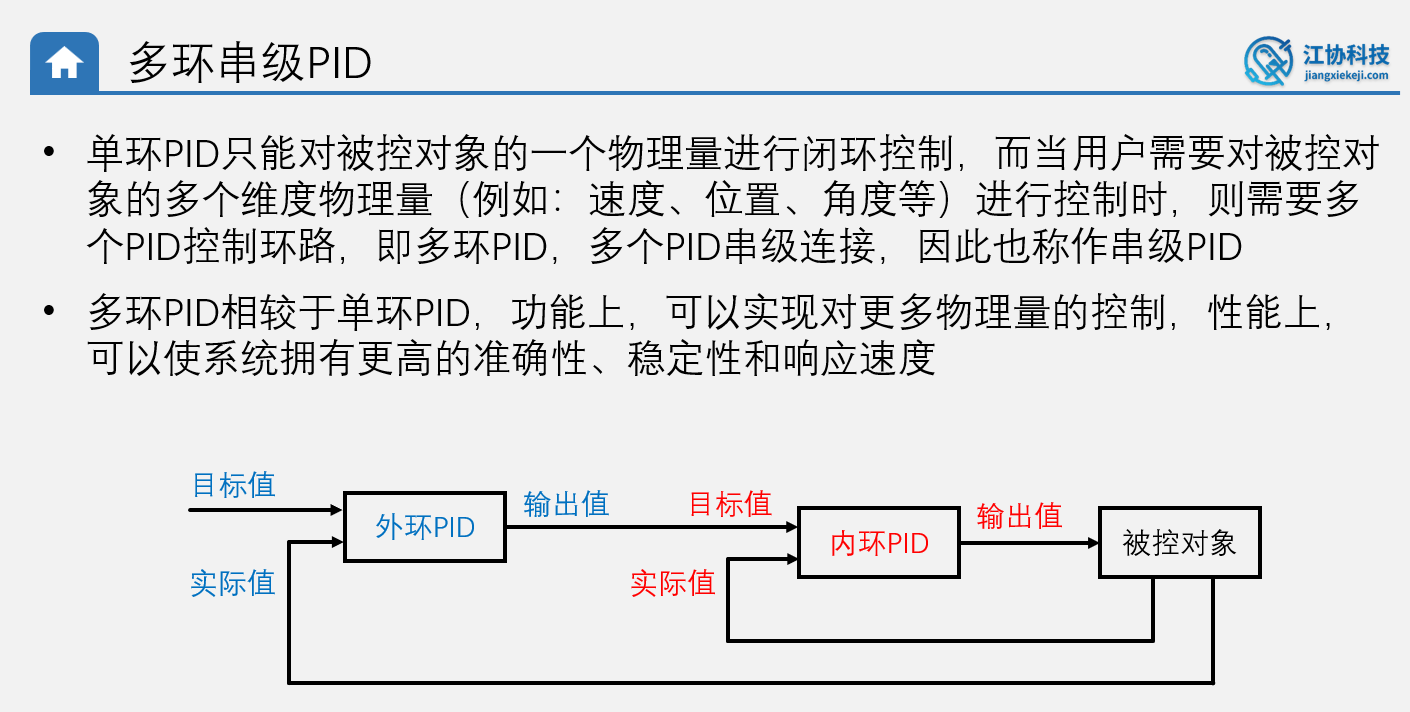
  • 关键所在：使用外环PID的输出值作为内环PID的目标值，但是内外环的PID的实际值都会返还给当前环
  • 可以对更多物理量进行控制，性能更好，比如可以实现点击定速定位控制，也就是让电机以指定速度来到指定位置停下来
单双环对比
  • 双环PID相当于单环PID自带一个定速控制的电机，而且位置环想控制位置时输出一个值给速度环，当实际位置与目标位置越接近时，位置环输出越小，速度环目标速度也就越小直到为0，此时电机达到指定位置而且速度也为0
  • 不存在启动力度过小电机转不起来的问题，因为位置环的目标位置设置很小时输出值给到了PI控制的速度环，由于是PI控制那么只要有目标速度而且目标位置与实际位置存在误差电机一定为转动而且最终会与目标位置重合
  • 抵抗外力的作用更强，因为施加外力时，速度环的目标速度应该为0，却由于外力产生实际速度，有了误差就会PI调控产生一个阻力对抗外力，而且又存在位置环，施加外力导致位置改变，位置环又要产生负向输出值给到速度环，让速度环的误差变大，速度环的积分项就会更大从而产生更大的对抗力
  • 优点也就是响应速度快，稳定性好，准确性高

调参顺序 ：先内环后外环

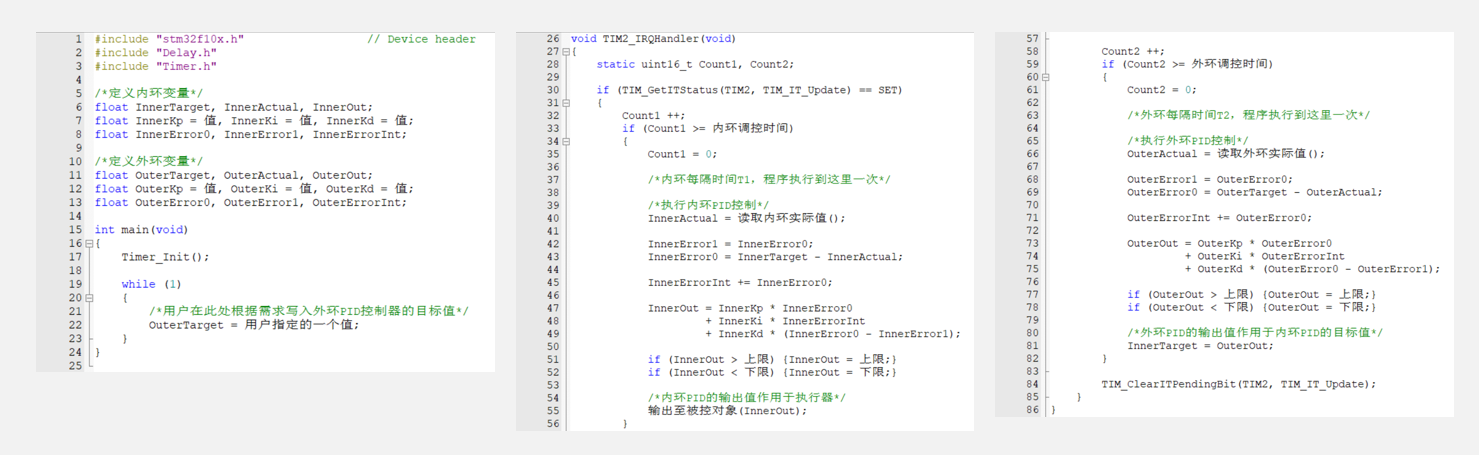
  • 内环和外环调控周期可以不同，可以设计总PID调控周期，然后在里面分别设置内环外环的调控周期
  • ++一般外环调控周期大于或等于内环，一是因为外环输出值刷新很快内环读取不过来没什么意义，二是因为内环一般调控反应更快的物理量，频率更大++
  • 需要修改内环PID的积分阈值，为外环的目标值的阈值，然后加上InnerTarget=OuterOut
  • 修改内环参数时，先要取消外环对内环的控制，也就是注释这一句InnerTarget=OuterOut
  • 修改内环的速度可以修改内环数值的积分限幅幅值

6.调参技巧

  • Kp：不断改变目标值观察实际值，然后逐步增大Kp直到实际值开始抖动，然后适当减小KP让抖动消失，此时Kp就比较适合
  • Ki ：看消除稳态误差的速度不满不满意，不满意就加大Ki但是不能够出现大幅度超调
  • Kd：太大会出现振荡，调节PD时，可以将P参数给大一点也没啥，超调可以用D来调节但是不能振荡，如果振荡就要调小KP
  • 三个参数的值建议量程显示大一点，尤其是使用电位器时候由于电位器的抖动，三个参数并不能完全为0，会出现实际值仍然缓慢跟踪目标值，量程够大的话能够看见应该不是0
  • 学会取舍，参数越响应快但是抖动振荡越严重，参数小响应慢但是动作平滑

代码部分

PID.h

cpp 复制代码 
#include "stm32f10x.h"                  // Device header
#include "PID.h"

void PID_Update(PID_t *p)
{
	p->Error1 = p->Error0;
	p->Error0 = p->Target - p->Actual;
	
	if (p->Ki != 0)
	{
		p->ErrorInt += p->Error0;
	}
	else
	{
		p->ErrorInt = 0;
	}
	
	p->Out = p->Kp * p->Error0
		   + p->Ki * p->ErrorInt
		   + p->Kd * (p->Error0 - p->Error1);
	
	if (p->Out > p->OutMax) {p->Out = p->OutMax;}
	if (p->Out < p->OutMin) {p->Out = p->OutMin;}
}

PID.h

cpp 复制代码 
#ifndef __PID_H
#define __PID_H

typedef struct {
	float Target;
	float Actual;
	float Out;
	
	float Kp;
	float Ki;
	float Kd;
	
	float Error0;
	float Error1;
	float ErrorInt;
	
	float OutMax;
	float OutMin;
} PID_t;

void PID_Update(PID_t *p);

#endif
相关推荐
Cc00108523 小时前
【AI学习笔记】用AI生成spring boot + redis
spring boot·笔记·学习·ai编程
繁花与尘埃3 小时前
列表标签之有序标签(本文为个人学习笔记，内容整理自哔哩哔哩UP主【非学者勿扰】的公开课程。 ＞ 所有知识点归属原作者，仅作非商业用途分享)
笔记·学习
lljss20203 小时前
5. 神经网络的学习
人工智能·神经网络·学习
MYX_3094 小时前
第五章 神经网络的优化
pytorch·深度学习·神经网络·学习
Lester_11014 小时前
嵌入式学习笔记- 单片机的低功耗以及唤醒
单片机·嵌入式硬件
Zzz 小生4 小时前
**编程基础学习(二)-C语言变量、控制结构和函数
笔记·学习
武清伯MVP4 小时前
阮一峰《TypeScript 教程》学习笔记——基本用法
笔记·学习·typescript
奋斗的阿狸_19864 小时前
nuttx实战项目2：蓝牙有线通信板之一，nsh串口调试
stm32·单片机·嵌入式硬件
en.en..4 小时前
STM32 定时中断逻辑拆解：为什么 “每 2 次中断翻一次 LED”，却是 1 秒亮 1 秒灭？
单片机·嵌入式硬件
热门推荐
01两千字总结：Codex 国内如何安装和使用的教程，以及如何设置中文回答02BongoCat - 跨平台键盘猫动画工具03GitHub 镜像站点04UV安装并设置国内源05Linux下V2Ray安装配置指南06GitLab 零基础入门指南：从安装到项目管理全流程07智能库存管理的需求预测模型：从业务痛点到落地代码的完整实践0846个Nano-banana 精选提示词，持续更新中092025羊城杯网络安全大赛 wp10Cursor Plan Mode：AI 终于知道先想后做了