【LeetCode】74. 搜索二维矩阵

熬了夜的程序员2025-10-17 8:43

文章目录

74. 搜索二维矩阵

题目描述

给你一个满足下述两条属性的 m x n 整数矩阵：

每行中的整数从左到右按非严格递增顺序排列。

每行的第一个整数大于前一行的最后一个整数。

给你一个整数 target ，如果 target 在矩阵中，返回 true ；否则，返回 false 。

示例 1：

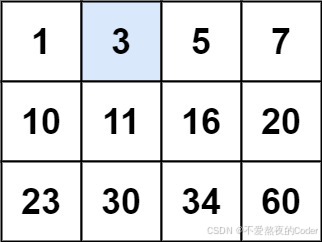
输入：matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 3

输出：true

示例 2：

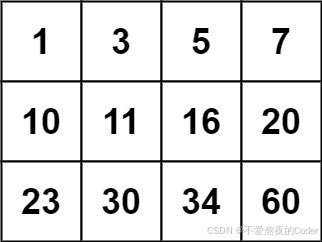
输入：matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 13

输出：false

提示：

  • m == matrix.length
  • n == matrix[i].length
  • 1 <= m, n <= 100
  • -10^4 <= matrix[i][j], target <= 10^4

解题思路

问题深度分析

这是一道二分查找 的经典问题，核心在于利用矩阵的有序性 。矩阵的特殊性质（每行递增，且每行首元素大于前一行末元素）使得整个矩阵可以看作一维有序数组。

问题本质

给定一个特殊的m×n矩阵：

  1. 每行从左到右递增
  2. 每行首元素 > 前一行末元素

这意味着矩阵整体是有序的 ，就像把一维有序数组按行切分。因此可以用二分查找在O(log(mn))时间内找到目标值。

核心思想

将二维矩阵映射为一维数组：

  • 矩阵索引(i, j) ↔ 一维索引k = i * n + j
  • 一维索引k ↔ 矩阵索引(k / n, k % n)
  • 对一维索引进行二分查找

关键映射关系：

复制代码 
二维 → 一维: index = row * n + col
一维 → 二维: row = index / n, col = index % n
关键难点分析

难点1：理解矩阵的有序性

  • 不仅每行有序，整个矩阵也有序
  • matrix[i][n-1] < matrix[i+1][0]（关键性质）
  • 可以将矩阵"展平"为一维数组

难点2：坐标映射

  • 二分查找在一维索引上进行
  • 需要正确转换一维索引到二维坐标
  • row = mid / n, col = mid % n

难点3：多种解法的选择

  • 一维二分（最优）：O(log(mn))
  • 两次二分：先找行，再找列，O(log m + log n)
  • 从右上角搜索：O(m + n)
  • 暴力搜索：O(mn)
典型情况分析

情况1：目标在矩阵中

复制代码 
matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]]
target = 3
一维视图: [1,3,5,7,10,11,16,20,23,30,34,60]
二分查找找到索引1 → (0, 1) → matrix[0][1] = 3
返回: true

情况2：目标不在矩阵中

复制代码 
matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]]
target = 13
一维视图: [1,3,5,7,10,11,16,20,23,30,34,60]
二分查找未找到
返回: false

情况3：目标小于最小值

复制代码 
matrix = [[1,3,5,7]]
target = 0
直接返回: false

情况4：目标大于最大值

复制代码 
matrix = [[1,3,5,7]]
target = 10
直接返回: false

情况5：单行或单列

复制代码 
matrix = [[1,3,5,7]] (单行)
相当于一维二分查找

matrix = [[1],[3],[5],[7]] (单列)
也可用一维二分
算法对比
算法 时间复杂度 空间复杂度 特点
一维二分 O(log(mn)) O(1) 最优解法
两次二分 O(log m+log n) O(1) 先定位行，再定位列
右上角搜索 O(m+n) O(1) 类似搜索树遍历
暴力搜索 O(mn) O(1) 遍历所有元素

注：m为行数，n为列数

算法流程图

主算法流程（一维二分）

是 否 否 是 是 否 是 否 开始: matrix, target 矩阵为空? 返回false 获取m行, n列 初始化: left=0, right=m*n-1 left <= right? 返回false 未找到 计算mid = left+right/2 转换坐标: row=mid/n, col=mid%n 获取midVal = matrix row col midVal == target? 返回true 找到 midVal < target? left = mid + 1 right = mid - 1

坐标映射详细流程
graph TD A[坐标映射] --> B[二维→一维] B --> C[index = row * n + col] C --> D[示例: row=1,col=2,n=4] D --> E[index = 1*4+2 = 6] A --> F[一维→二维] F --> G[row = index / n] F --> H[col = index % n] G --> I[示例: index=6,n=4] H --> I I --> J[row = 6/4 = 1] I --> K[col = 6%4 = 2] J --> L[结果: row,col = 1,2] K --> L
两次二分查找流程

是 否 两次二分 第一次: 找目标行 二分查找每行的首元素 找到target可能所在的行 第二次: 在该行中二分 标准一维二分查找 找到? 返回true 返回false

复杂度分析

时间复杂度详解

一维二分：O(log(mn))

  • 将m×n矩阵看作mn个元素的数组
  • 二分查找：O(log(mn))
  • 坐标转换：O(1)

两次二分：O(log m + log n)

  • 第一次二分找行：O(log m)
  • 第二次二分找列：O(log n)
  • 总时间：O(log m + log n) ≈ O(log(mn))

右上角搜索：O(m + n)

  • 最坏情况从右上到左下
  • 每步排除一行或一列
  • 总步数：m + n - 1
空间复杂度详解

所有方法：O(1)

  • 只用常量级额外变量
  • 不需要额外数组

关键优化技巧

技巧1：一维二分（最优解法）
go 复制代码 
func searchMatrix(matrix [][]int, target int) bool {
    if len(matrix) == 0 || len(matrix[0]) == 0 {
        return false
    }
    
    m, n := len(matrix), len(matrix[0])
    left, right := 0, m*n-1
    
    for left <= right {
        mid := left + (right-left)/2
        
        // 关键：一维索引转二维坐标
        row := mid / n
        col := mid % n
        midVal := matrix[row][col]
        
        if midVal == target {
            return true
        } else if midVal < target {
            left = mid + 1
        } else {
            right = mid - 1
        }
    }
    
    return false
}

优势：

  • 时间复杂度最优：O(log(mn))
  • 代码简洁
  • 充分利用矩阵有序性
技巧2：两次二分（先行后列）
go 复制代码 
func searchMatrix(matrix [][]int, target int) bool {
    if len(matrix) == 0 || len(matrix[0]) == 0 {
        return false
    }
    
    m, n := len(matrix), len(matrix[0])
    
    // 第一次二分：找目标行
    top, bottom := 0, m-1
    targetRow := -1
    
    for top <= bottom {
        mid := top + (bottom-top)/2
        
        if matrix[mid][0] <= target && target <= matrix[mid][n-1] {
            targetRow = mid
            break
        } else if matrix[mid][0] > target {
            bottom = mid - 1
        } else {
            top = mid + 1
        }
    }
    
    if targetRow == -1 {
        return false
    }
    
    // 第二次二分：在目标行中查找
    left, right := 0, n-1
    
    for left <= right {
        mid := left + (right-left)/2
        
        if matrix[targetRow][mid] == target {
            return true
        } else if matrix[targetRow][mid] < target {
            left = mid + 1
        } else {
            right = mid - 1
        }
    }
    
    return false
}

特点：

  • 逻辑清晰，分两步
  • 时间复杂度：O(log m + log n)
技巧3：从右上角搜索（类似BST）
go 复制代码 
func searchMatrix(matrix [][]int, target int) bool {
    if len(matrix) == 0 || len(matrix[0]) == 0 {
        return false
    }
    
    m, n := len(matrix), len(matrix[0])
    row, col := 0, n-1  // 从右上角开始
    
    for row < m && col >= 0 {
        if matrix[row][col] == target {
            return true
        } else if matrix[row][col] > target {
            col--  // 当前值太大，向左移
        } else {
            row++  // 当前值太小，向下移
        }
    }
    
    return false
}

特点：

  • 类似二叉搜索树的搜索
  • 每步排除一行或一列
  • 时间O(m+n)，不如二分
技巧4：暴力搜索（对比用）
go 复制代码 
func searchMatrix(matrix [][]int, target int) bool {
    for i := 0; i < len(matrix); i++ {
        for j := 0; j < len(matrix[0]); j++ {
            if matrix[i][j] == target {
                return true
            }
        }
    }
    return false
}

说明：O(mn)，仅用于理解问题

边界情况处理

  1. 空矩阵 ：matrix = [] 或 matrix = [[]] → false
  2. 单个元素 ：
    • matrix = [[5]], target = 5 → true
    • matrix = [[5]], target = 3 → false
  3. 单行 ：matrix = [[1,3,5]], target = 3 → true
  4. 单列 ：matrix = [[1],[3],[5]], target = 3 → true
  5. 目标在边界 ：
    • 左上角：matrix[0][0]
    • 右下角：matrix[m-1][n-1]
  6. 目标超出范围 ：
    • 小于最小值
    • 大于最大值

测试用例设计

基础测试
复制代码 
输入: matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 3
输出: true
说明: 目标在第一行
目标不存在
复制代码 
输入: matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 13
输出: false
说明: 13在10和16之间，但不在矩阵中
单个元素
复制代码 
输入: matrix = [[5]], target = 5
输出: true
说明: 矩阵只有一个元素
边界测试
复制代码 
输入: matrix = [[1,3,5,7]], target = 1
输出: true
说明: 目标是最小值

输入: matrix = [[1,3,5,7]], target = 7
输出: true
说明: 目标是最大值

常见错误与陷阱

错误1：坐标转换错误
go 复制代码 
// ❌ 错误：行列计算反了
row := mid % n  // 错误
col := mid / n  // 错误

// ✅ 正确：
row := mid / n  // 行 = 索引 / 列数
col := mid % n  // 列 = 索引 % 列数
错误2：边界条件未处理
go 复制代码 
// ❌ 错误：没有检查空矩阵
m, n := len(matrix), len(matrix[0])  // 可能越界

// ✅ 正确：先检查
if len(matrix) == 0 || len(matrix[0]) == 0 {
    return false
}
错误3：二分查找边界错误
go 复制代码 
// ❌ 错误：right初始化错误
right := m * n  // 应该是 m*n-1

// ✅ 正确：
right := m*n - 1
错误4：误把240题的方法用在这里
go 复制代码 
// ❌ 错误：本题不适合从左下或右上搜索（虽然可以）
// 240题矩阵性质不同，本题有更强的有序性
// 应该用二分查找，不是O(m+n)的搜索

// ✅ 正确：用一维二分，O(log(mn))

实战技巧总结

  1. 识别矩阵性质：每行递增 + 行间连续 = 整体有序
  2. 坐标映射 ：index = row*n + col，row = index/n, col = index%n
  3. 二分边界 ：left=0, right=m*n-1
  4. 优先选择：一维二分最优，代码简洁
  5. 避免混淆：本题(74)与240题不同，240题每行每列递增但行间不连续
  6. 处理空矩阵 ：先检查len(matrix)==0

与240题的区别

74题（本题）：

  • 每行递增
  • 每行首 > 前一行尾（关键）
  • 整体有序，可一维二分：O(log(mn))

240题：

  • 每行递增
  • 每列递增
  • 行间无序
  • 只能从角落搜索：O(m+n)

进阶扩展

扩展1：返回目标位置
go 复制代码 
func searchMatrixPosition(matrix [][]int, target int) []int {
    if len(matrix) == 0 || len(matrix[0]) == 0 {
        return []int{-1, -1}
    }
    
    m, n := len(matrix), len(matrix[0])
    left, right := 0, m*n-1
    
    for left <= right {
        mid := left + (right-left)/2
        row := mid / n
        col := mid % n
        
        if matrix[row][col] == target {
            return []int{row, col}
        } else if matrix[row][col] < target {
            left = mid + 1
        } else {
            right = mid - 1
        }
    }
    
    return []int{-1, -1}
}
扩展2：找第k小的元素
go 复制代码 
func kthSmallest(matrix [][]int, k int) int {
    m, n := len(matrix), len(matrix[0])
    
    if k < 1 || k > m*n {
        return -1
    }
    
    // 矩阵整体有序，第k小就是第k-1个索引
    index := k - 1
    row := index / n
    col := index % n
    
    return matrix[row][col]
}
扩展3：统计小于target的元素个数
go 复制代码 
func countLessThan(matrix [][]int, target int) int {
    if len(matrix) == 0 || len(matrix[0]) == 0 {
        return 0
    }
    
    m, n := len(matrix), len(matrix[0])
    left, right := 0, m*n-1
    result := 0
    
    for left <= right {
        mid := left + (right-left)/2
        row := mid / n
        col := mid % n
        
        if matrix[row][col] < target {
            result = mid + 1  // mid及之前的都小于target
            left = mid + 1
        } else {
            right = mid - 1
        }
    }
    
    return result
}

应用场景

  1. 数据库索引：有序表的快速查找
  2. 分布式存储：数据分片后的定位
  3. 游戏开发：地图网格的快速搜索
  4. 图像处理：像素矩阵的值查找
  5. 算法竞赛：二分查找的变形应用

代码实现

本题提供了四种不同的解法，重点掌握一维二分查找方法。

测试结果

测试用例 一维二分 两次二分 右上角搜索 暴力搜索
基础测试 ✅ ✅ ✅ ✅
目标不存在 ✅ ✅ ✅ ✅
单个元素 ✅ ✅ ✅ ✅
边界测试 ✅ ✅ ✅ ✅

核心收获

  1. 矩阵有序性：每行递增+行间连续 = 整体有序
  2. 坐标映射：二维↔一维的转换公式
  3. 二分查找：在"虚拟"一维数组上二分
  4. 时间复杂度：O(log(mn))是最优解
  5. 与240题区别：本题整体有序，240题只是行列有序

应用拓展

  • 有序矩阵的快速查找
  • 数据库索引优化
  • 分布式系统的数据定位
  • 二维数据的二分搜索

完整题解代码

go 复制代码 
package main

import "fmt"

// =========================== 方法一：一维二分（最优解法） ===========================

func searchMatrix(matrix [][]int, target int) bool {
	if len(matrix) == 0 || len(matrix[0]) == 0 {
		return false
	}

	m, n := len(matrix), len(matrix[0])
	left, right := 0, m*n-1

	for left <= right {
		mid := left + (right-left)/2

		// 关键：一维索引转二维坐标
		row := mid / n
		col := mid % n
		midVal := matrix[row][col]

		if midVal == target {
			return true
		} else if midVal < target {
			left = mid + 1
		} else {
			right = mid - 1
		}
	}

	return false
}

// =========================== 方法二：两次二分 ===========================

func searchMatrix2(matrix [][]int, target int) bool {
	if len(matrix) == 0 || len(matrix[0]) == 0 {
		return false
	}

	m, n := len(matrix), len(matrix[0])

	// 第一次二分：找目标行
	top, bottom := 0, m-1
	targetRow := -1

	for top <= bottom {
		mid := top + (bottom-top)/2

		if matrix[mid][0] <= target && target <= matrix[mid][n-1] {
			targetRow = mid
			break
		} else if matrix[mid][0] > target {
			bottom = mid - 1
		} else {
			top = mid + 1
		}
	}

	if targetRow == -1 {
		return false
	}

	// 第二次二分：在目标行中查找
	left, right := 0, n-1

	for left <= right {
		mid := left + (right-left)/2

		if matrix[targetRow][mid] == target {
			return true
		} else if matrix[targetRow][mid] < target {
			left = mid + 1
		} else {
			right = mid - 1
		}
	}

	return false
}

// =========================== 方法三：从右上角搜索 ===========================

func searchMatrix3(matrix [][]int, target int) bool {
	if len(matrix) == 0 || len(matrix[0]) == 0 {
		return false
	}

	m, n := len(matrix), len(matrix[0])
	row, col := 0, n-1 // 从右上角开始

	for row < m && col >= 0 {
		if matrix[row][col] == target {
			return true
		} else if matrix[row][col] > target {
			col-- // 当前值太大，向左移
		} else {
			row++ // 当前值太小，向下移
		}
	}

	return false
}

// =========================== 方法四：暴力搜索 ===========================

func searchMatrix4(matrix [][]int, target int) bool {
	for i := 0; i < len(matrix); i++ {
		for j := 0; j < len(matrix[0]); j++ {
			if matrix[i][j] == target {
				return true
			}
		}
	}
	return false
}

// =========================== 测试代码 ===========================

func main() {
	fmt.Println("=== LeetCode 74: 搜索二维矩阵 ===\n")

	testCases := []struct {
		matrix [][]int
		target int
		expect bool
	}{
		{
			[][]int{{1, 3, 5, 7}, {10, 11, 16, 20}, {23, 30, 34, 60}},
			3,
			true,
		},
		{
			[][]int{{1, 3, 5, 7}, {10, 11, 16, 20}, {23, 30, 34, 60}},
			13,
			false,
		},
		{
			[][]int{{5}},
			5,
			true,
		},
		{
			[][]int{{5}},
			3,
			false,
		},
		{
			[][]int{{1, 3, 5, 7}},
			1,
			true,
		},
		{
			[][]int{{1, 3, 5, 7}},
			7,
			true,
		},
		{
			[][]int{{1}, {3}, {5}, {7}},
			3,
			true,
		},
	}

	fmt.Println("方法一：一维二分（最优解法）")
	runTests(testCases, searchMatrix)

	fmt.Println("\n方法二：两次二分")
	runTests(testCases, searchMatrix2)

	fmt.Println("\n方法三：从右上角搜索")
	runTests(testCases, searchMatrix3)

	fmt.Println("\n方法四：暴力搜索")
	runTests(testCases, searchMatrix4)
}

func runTests(testCases []struct {
	matrix [][]int
	target int
	expect bool
}, fn func([][]int, int) bool) {
	passCount := 0
	for i, tc := range testCases {
		result := fn(tc.matrix, tc.target)
		status := "✅"
		if result != tc.expect {
			status = "❌"
		} else {
			passCount++
		}
		fmt.Printf("  测试%d: %s\n", i+1, status)
		if status == "❌" {
			fmt.Printf("    矩阵: %v, 目标: %d\n", tc.matrix, tc.target)
			fmt.Printf("    输出: %v\n", result)
			fmt.Printf("    期望: %v\n", tc.expect)
		}
	}
	fmt.Printf("  通过: %d/%d\n", passCount, len(testCases))
}
相关推荐
丁浩6662 小时前
Python机器学习---2.算法：逻辑回归
python·算法·机器学习
伏小白白白3 小时前
【论文精度-2】求解车辆路径问题的神经组合优化算法:综合展望（Yubin Xiao，2025）
人工智能·算法·机器学习
无敌最俊朗@3 小时前
数组-力扣hot56-合并区间
数据结构·算法·leetcode
囚生CY4 小时前
【速写】优化的深度与广度（Adam & Moun）
人工智能·python·算法
码农多耕地呗4 小时前
力扣94.二叉树的中序遍历（递归and迭代法）（java）
数据结构·算法·leetcode
微笑尅乐4 小时前
BFS 与 DFS——力扣102.二叉树的层序遍历
leetcode·深度优先·宽度优先
懒羊羊不懒@4 小时前
Java基础语法—最小单位、及注释
java·c语言·开发语言·数据结构·学习·算法
白云千载尽5 小时前
leetcode 912.排序数组
算法·leetcode·职场和发展
哆啦刘小洋5 小时前
Tips：预封装约束的状态定义
算法
代码充电宝5 小时前
LeetCode 算法题【简单】290. 单词规律
java·算法·leetcode·职场和发展·哈希表
热门推荐
01BongoCat - 跨平台键盘猫动画工具02GitHub 镜像站点03UV安装并设置国内源04Linux下V2Ray安装配置指南05KGG转MP3工具|非KGM文件|解密音频06两千字总结：Codex 国内如何安装和使用的教程，以及如何设置中文回答07荣耀手机2025年10月发布的新品Magic8比起Magic7，在硬件、性能、价格等上有什么区别，有什么优势08GitLab 零基础入门指南：从安装到项目管理全流程09windows找不到gpedit.msc（本地组策略编辑器）10Java IO 流 + MinIO：游戏玩家自定义头像上传（格式校验、压缩处理、存储管理）