////// 欢迎来到 aramae 的博客,愿 Bug 远离,好运常伴! //////
博主的Gitee地址: 阿拉美 (aramae) - Gitee.com
时代不会辜负长期主义者,愿每一个努力的人都能达到理想的彼岸。
目录
[一. 基础知识](#一. 基础知识)
[简单分析 RBTree](#简单分析 RBTree)
[1. 旋转](#1. 旋转)
[2. 插入(Insertion)](#2. 插入(Insertion))
[Case 1: 叔父节点U是红色](#Case 1: 叔父节点U是红色)
[Case 2: 叔父节点U是黑色,且C是右孩子(三角形结构)](#Case 2: 叔父节点U是黑色,且C是右孩子(三角形结构))
[Case 3: 叔父节点U是黑色,且C是左孩子(直线结构)](#Case 3: 叔父节点U是黑色,且C是左孩子(直线结构))
[二. RBTree插入操作 (迭代实现)](#二. RBTree插入操作 (迭代实现))
[1. 基本数据结构](#1. 基本数据结构)
[2. 插入操作 - 第一部分:BST插入](#2. 插入操作 - 第一部分:BST插入)
[3. 插入操作 - 第二部分:红黑树修复](#3. 插入操作 - 第二部分:红黑树修复)
[4. 旋转操作详解](#4. 旋转操作详解)
[5. 平衡性检查](#5. 平衡性检查)
[三. RBTree 与 AVLTree 的 比较分析](#三. RBTree 与 AVLTree 的 比较分析)
[四. RBTree的递归实现(补充)完整实现](#四. RBTree的递归实现(补充)完整实现)
一. 基础知识
红黑树是一种自平衡的二叉查找树 。它在二叉查找树的基础上,在每个节点上增加了一个存储位来表示节点的颜色(红色或黑色)。通过对任何一条从根到叶子的路径上各个节点着色方式的限制,红黑树确保没有一条路径会比其他路径长出两倍 ,因而是近似平衡的。
它的主要价值在于,它能够在最坏情况 下,依然保证查找、插入、删除 等操作的时间复杂度为 O(log n)。
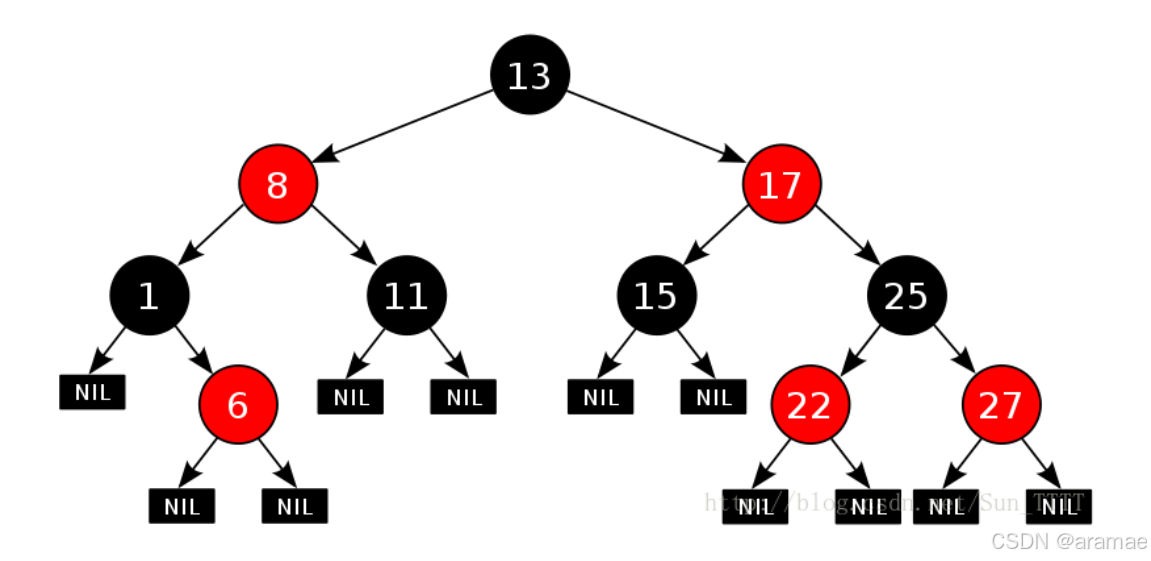
红黑树的五个性质:
-
每个节点是红色或黑色。
-
根节点是黑色。
-
所有叶子节点(NIL节点)都是黑色。
-
每个红色节点的两个子节点都是黑色(即不能有两个连续的红色节点)。
-
从任意节点到其每个叶子节点的所有路径都包含相同数目的黑色节点。
注意:在实现中,我们通常将空节点视为NIL节点,它们都是黑色的。
注:(红黑树的删除操作 步骤会更为复杂一些,本章暂不做分析,本文主讲迭代实现的红黑树的插入操作,文末会给出完整的递归实现的 RBTree.h(包括删除操作),在普通学习阶段 递归版本会更多一些,但二者的核心操作原理是一致的,当理解了迭代实现后,递归的也不会太难理解)
总结:本文主要介绍 RBTree插入操作的迭代实现 ,补充 RBTree完整递归实现 ;
后续博主会更新完整的迭代版本的RBTree实现(当然不在这个专栏了,感兴趣的敬请期待 ~~~) (~ ^ \/ ^ )~
简单分析 RBTree
- 1.根节点是黑的(硬性条件)
- 2.每个节点要么是黑色,要么是红色
- 3**.所有叶子节点(NIL节点)都是黑色的**(在实现中,我们通常把空指针视为黑色的NIL节点)
-
- 最关键的性质 红色节点的两个子节点都是黑色的(不能有连续的红色节点)
- 5.平衡性的核心 从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点
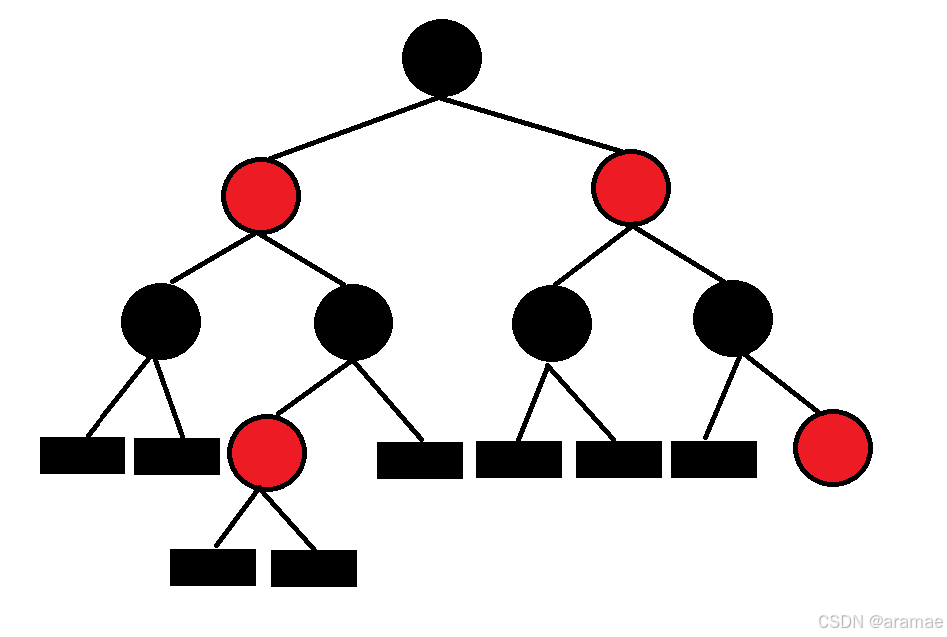
-
最短路径:全部是黑色结点
-
最长路径:红黑相间(一黑一红,最后一个非NIL结点可以是红)
-
去掉红色结点的红黑树接近一棵满二叉树.(直接去掉红色结点可能就不是二叉树了,hold不住)
-
当只有一个根节点时(黑),第二个结点只能是红色(满足黑结点数量相同),被迫只能插入红色结点.
-
新增结点默认为红色,红色规则比黑色宽松
数学关系
-
最短路径:全黑节点
-
最长路径:红黑交替
-
由于黑高相同,最长路径 ≤ 2 × 最短路径
核心算法要点总结
为了维持上述五大性质,在插入和删除节点后,我们需要对树进行调整。调整的核心操作有两种:旋转(Rotation) 和 变色(Recoloring)。
1. 旋转
旋转是局部调整树结构,保持二叉查找树性质(左<中<右)的操作。
-
左旋(Left Rotate): 以某个节点为支点,其右子节点成为新的父节点。
-
右旋(Right Rotate): 以某个节点为支点,其左子节点成为新的父节点。
2. 插入(Insertion)
红黑树的插入分为两个步骤:
-
标准BST插入 :像普通的二叉查找树一样,找到合适的位置插入新节点
Z。 -
调整与修复 :将新插入的节点初始颜色设置为红色,然后检查是否破坏了红黑树的性质。
为什么新插入的节点是红色?
因为如果插入黑色节点,必然会违反性质5(导致路径上黑色节点数不一致),修复起来非常困难。而插入红色节点,可能违反性质2(根节点为黑)或性质4(不能有连续红节点),修复起来相对简单。
检测新节点插入后,红黑树的性质是否造到破坏
因为新节点的默认颜色是红色 ,因此:如果其双亲节点的颜色是黑色,没有违反红黑树任何
性质 ,则不需要调整;但当新插入节点的双亲节点颜色为红色时,就违反了性质三不能有连
在一起的红色节点,此时需要对红黑树分情况来讨论:
约定:cur为当前节点,p为父节点,g为祖父节点,u为叔叔节点
插入后的修复情况分析:
红黑树插入修复只有3种基本情况:
Case 1 - 叔叔红:变色向上
Case 2 - 叔叔黑+孩子在右:左旋case3
Case 3 - 叔叔黑+孩子在左左:右旋修复
为什么是3种而不是更多?
分类标准:
按叔叔颜色:红色 vs 黑色
按当前节点位置:左孩子 vs 右孩子
组合结果:
U为红 → Case 1
U为黑 + C为左 → Case 3
U为黑 + C为右 → Case 2
修复过程是一个循环,只要不满足红黑树性质就持续调整。主要有以下三种情况:
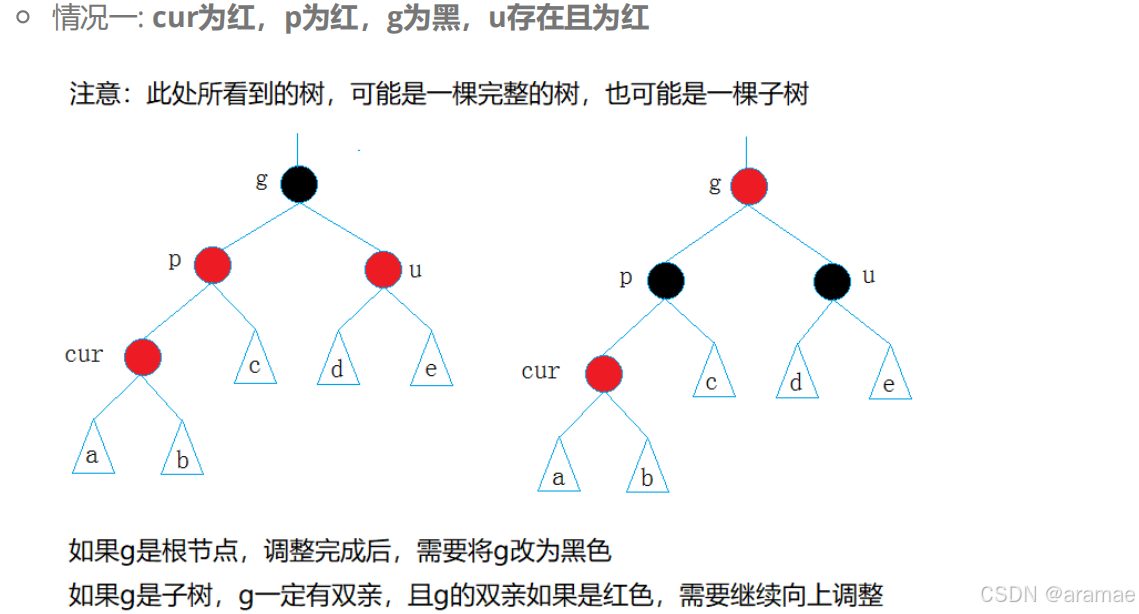
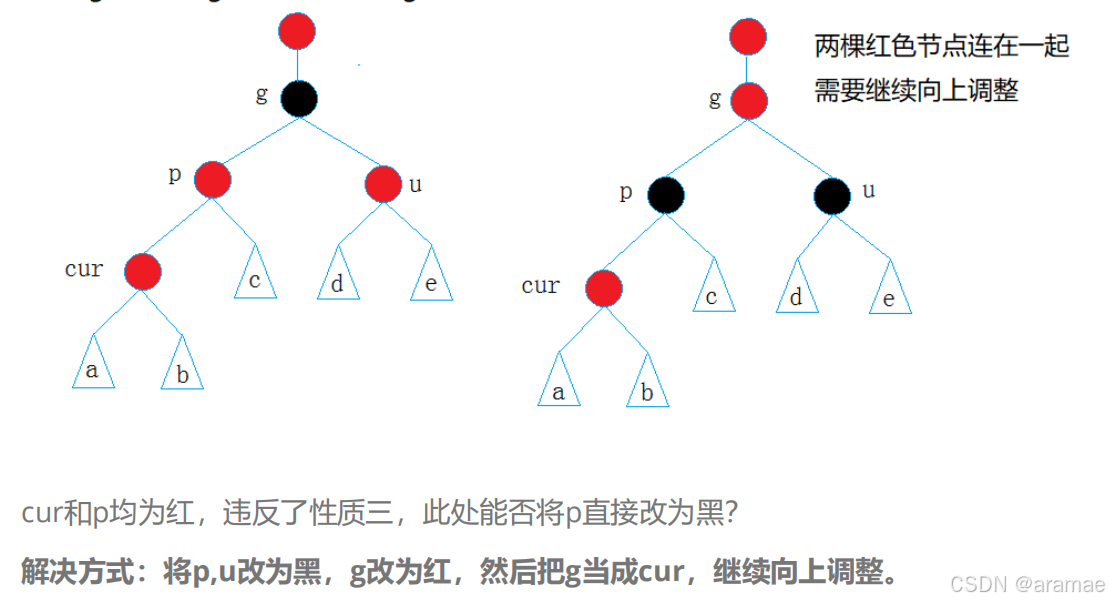
Case 1: 叔父节点U是红色
bash
操作:将父节点P和叔父节点U变为黑色,祖父节点G变为红色。
然后将当前节点C指向祖父节点G,从新的C开始继续向上修复。
解释:这相当于将"红色"向上推送,解决了局部连续红色的问题
,但可能让G和它的父节点形成连续红色。Case 2: 叔父节点U是黑色,且C是右孩子(三角形结构)
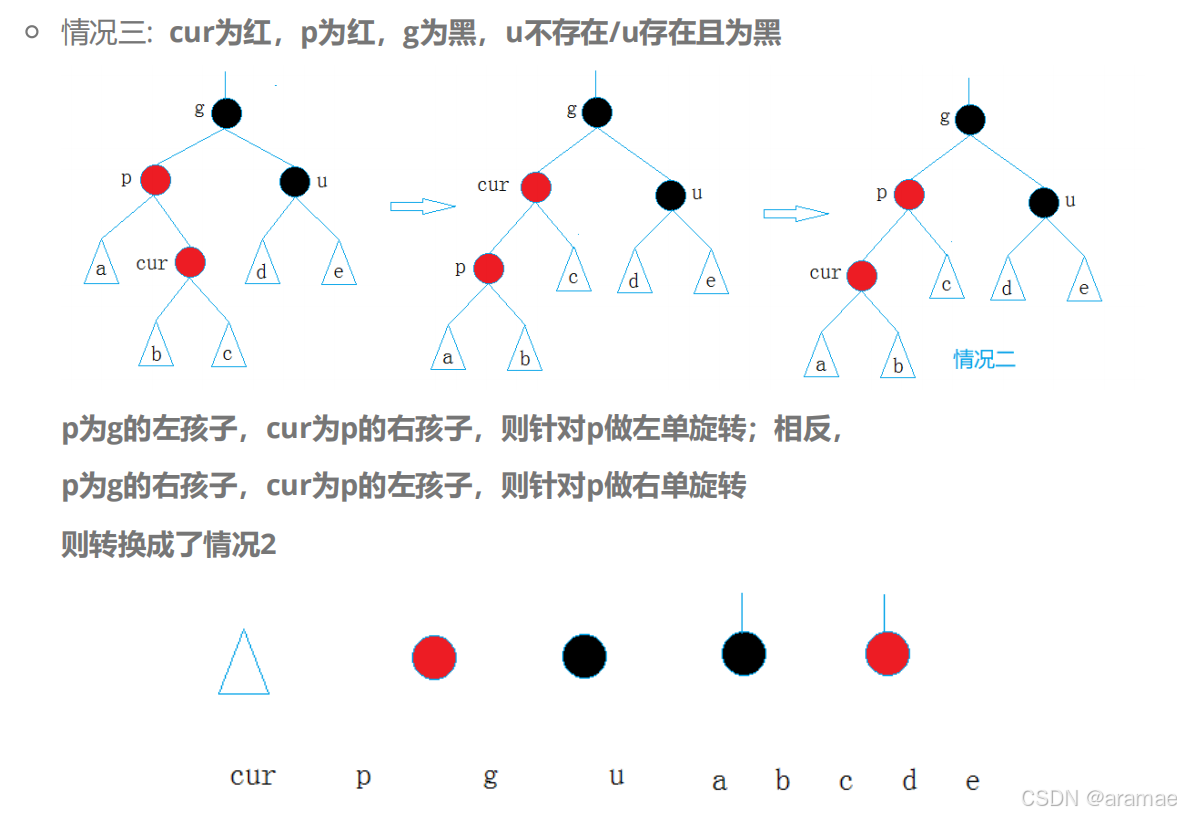
bash
操作:以父节点P为支点进行左旋,将情况转换为Case 3。
解释:通过旋转,将"三角形"的不平衡结构转换为"直线"结构,为后续的单旋转做准备。Case 3: 叔父节点U是黑色,且C是左孩子(直线结构)
bash
操作:将父节点P变为黑色,祖父节点G变为红色,然后以祖父节点G为支点进行右旋
解释:这是修复的最终步骤。通过变色和一次旋转,既消除了连续红色,又保持了黑高的平衡。
此时局部子树已平衡,修复完成。最后:无论经过何种情况,在修复循环结束后,将根节点强制设为黑色(以满足性质2)。
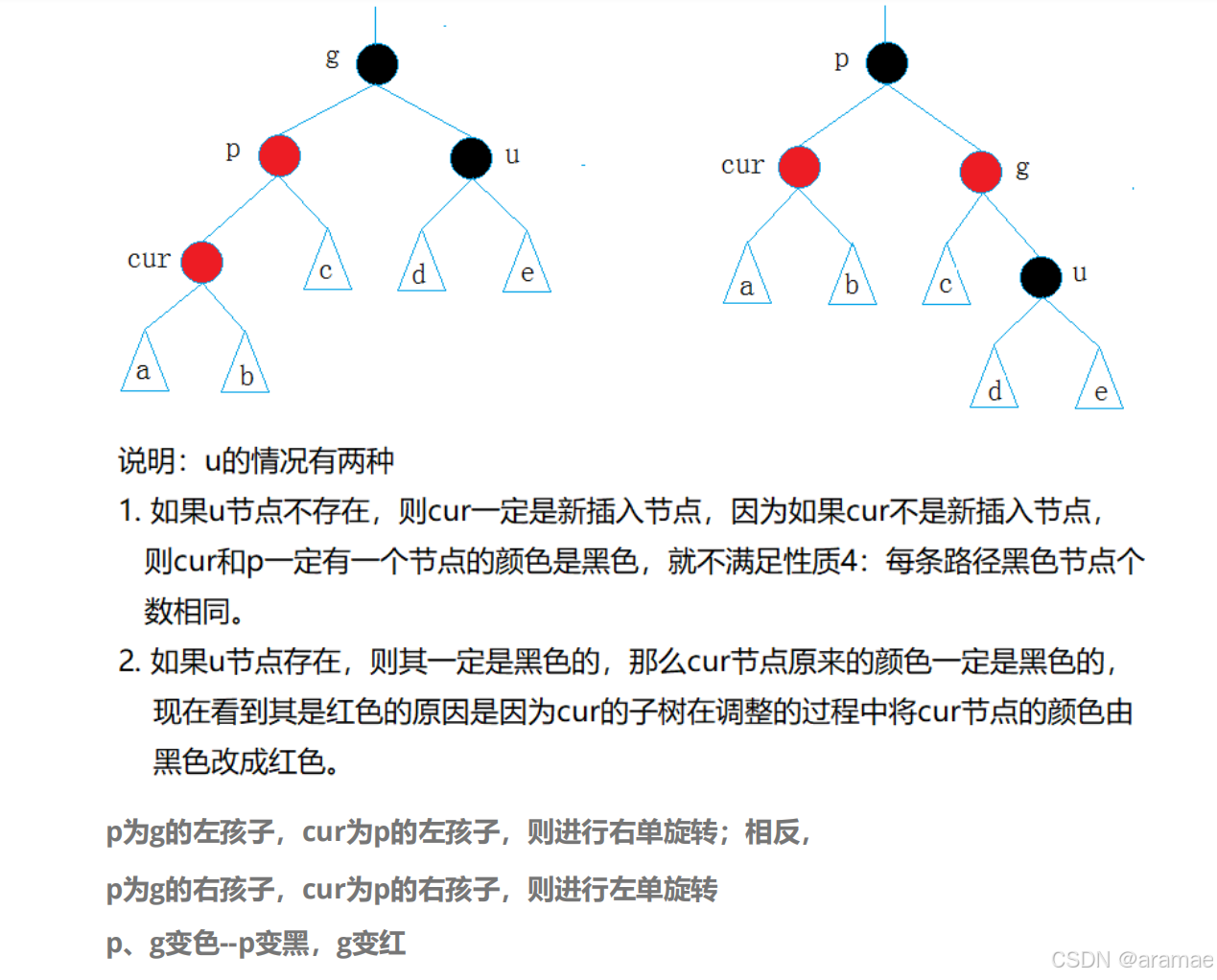
** 或许有人会提出疑问,那叔叔不存在的情况呢?
没有叔叔节点(uncle为nullptr)在红黑树中被视为黑色节点,所以这种情况已经包含在我们之前讨论的Case 2和Case 3中了。
为什么nullptr被视为黑色?
红黑树性质的要求
• 性质3:所有叶子节点(NIL节点)都是黑色的
• 在实现中,空指针就代表NIL节点
• 因此nullptr自然被视为黑色节点
XML
插入修复的三种情况:
情况1:叔叔为红色
黑(g)
/ \
红(p) 红(u)
/
红(c)
处理:变色
-> 红(g)
/ \
黑(p) 黑(u)
/
红(c)
情况2:LL型(叔叔为黑,当前节点是左孩子的左孩子)
黑(g)
/ \
红(p) 黑(u)
/
红(c)
处理:右旋 + 变色
-> 黑(p)
/ \
红(c) 红(g)
\
黑(u)
情况3:LR型(叔叔为黑,当前节点是左孩子的右孩子)
黑(g)
/ \
红(p) 黑(u)
\
红(c)
处理:先左旋p,再右旋g + 变色
cpp
插入新节点(红色)
↓
while (父节点是红色) {
if (叔父节点是红色) {
情况1: 颜色翻转
} else {
if (当前节点是右孩子) {
情况2: 左旋 → 情况3
}
情况3: 变色 + 右旋
}
}
根节点设为黑色二. RBTree插入操作 (迭代实现)
1. 基本数据结构
cpp
enum Colour
{
RED,
BLACK
};
template<class K, class V>
struct RBTreeNode
{
RBTreeNode<K, V>* _left;
RBTreeNode<K, V>* _right;
RBTreeNode<K, V>* _parent; // 父指针,便于回溯
pair<K, V> _kv;
Colour _col;
RBTreeNode(const pair<K, V>& kv)
:_left(nullptr)
,_right(nullptr)
,_parent(nullptr)
,_kv(kv)
,_col(RED) // 新节点总是红色
{}
};-
新节点默认是红色,这样不会破坏黑高平衡
-
包含父指针,便于在插入修复时向上回溯
思考:在节点的定义中,为什么要将节点的默认颜色给成红色的?
-
新节点为红:50%概率不需要调整(父节点为黑)
-
新节点为黑:100%概率需要调整(必然破坏黑高)
-
先插入:以红色插入,最小化初始破坏
-
后修复:根据需要逐步向上修复
2. 插入操作 - 第一部分:BST插入
cpp
bool Insert(const pair<K, V>& kv)
{
if (_root == nullptr)
{
_root = new Node(kv);
_root->_col = BLACK; // 根节点必须是黑色
return true;
}
Node* parent = nullptr;
Node* cur = _root;
// 标准的BST插入查找
while (cur)
{
if (cur->_kv.first < kv.first)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_kv.first > kv.first)
{
parent = cur;
cur = cur->_left;
}
else
{
return false; // 键已存在
}
}
// 创建新节点并连接到父节点
cur = new Node(kv);
cur->_col = RED;
if (parent->_kv.first < kv.first)
{
parent->_right = cur;
}
else
{
parent->_left = cur;
}
cur->_parent = parent;-
如果是空树,创建黑色根节点
-
否则,按BST规则找到插入位置
-
新节点总是红色,连接到父节点
3. 插入操作 - 第二部分:红黑树修复
这是最核心的部分,处理各种违反红黑树性质的情况
cpp
while (parent && parent->_col == RED)
{
Node* grandfather = parent->_parent;
if (parent == grandfather->_left) // 父节点是祖父的左孩子
{
Node* uncle = grandfather->_right;
// Case 1: 叔叔节点为红色
if (uncle && uncle->_col == RED)
{
// 变色处理
parent->_col = uncle->_col = BLACK;
grandfather->_col = RED;
// 向上回溯
cur = grandfather;
parent = cur->_parent;
}
else // Case 2 & 3: 叔叔节点为黑色或不存在
{
if (cur == parent->_left)
{
// Case 2: LL情况 - 单右旋
// g
// p
// c
RotateR(grandfather);
parent->_col = BLACK;
grandfather->_col = RED;
}
else
{
// Case 3: LR情况 - 先左旋后右旋
// g
// p
// c
RotateL(parent);
RotateR(grandfather);
cur->_col = BLACK;
grandfather->_col = RED;
}
break;
}
}
else // 对称情况:父节点是祖父的右孩子
{
// 对称处理...
}
}
_root->_col = BLACK; // 确保根节点为黑色4. 旋转操作详解
这部分的核心旋转操作和前章的AVL树的核心旋转操作一样,不做过多讲解;
左旋操作:
cpp
void RotateL(Node* parent)
{
++_rotateCount;
Node* cur = parent->_right; // 当前的右孩子将成为新的父节点
Node* curleft = cur->_left; // cur的左孩子
// 第一步:处理curleft
parent->_right = curleft;
if (curleft)
{
curleft->_parent = parent;
}
// 第二步:cur成为新的父节点
cur->_left = parent;
// 第三步:更新父指针
Node* ppnode = parent->_parent;
parent->_parent = cur;
// 第四步:更新祖父节点的指针
if (parent == _root)
{
_root = cur;
cur->_parent = nullptr;
}
else
{
if (ppnode->_left == parent)
{
ppnode->_left = cur;
}
else
{
ppnode->_right = cur;
}
cur->_parent = ppnode;
}
}旋转示意图:
bash
左旋前:
parent
/ \
A cur
/ \
curleft B
左旋后:
cur
/ \
parent B
/ \
A curleft右旋操作:
cpp
//右旋函数
void RotateR(Node* parent)
{
++_rotateCount;
Node* cur = parent->_left;
Node* curright = cur->_right;
parent->_left = curright;
if (curright)
curright->_parent = parent;
Node* ppnode = parent->_parent;
cur->_right = parent;
parent->_parent = cur;
if (ppnode == nullptr)
{
_root = cur;
cur->_parent = nullptr;
}
else
{
if (ppnode->_left == parent)
{
ppnode->_left = cur;
}
else
{
ppnode->_right = cur;
}
cur->_parent = ppnode;
}
}旋转示意图:
bash
右旋前:
parent
/ \
cur A
/ \
B curright
右旋后:
cur
/ \
B parent
/ \
curright A插入操作汇总:
cpp
bool Insert(const pair<K, V>& kv) {
if (_root == nullptr) {
_root = new Node(kv);
_root->_col = BLACK;
return true;
}
Node* parent = nullptr;
Node* cur = _root;
while (cur) {
if (cur->_kv.first < kv.first) {
parent = cur;
cur = cur->_right;
}
else if (cur->_kv.first > kv.first) {
parent = cur;
cur = cur->_left;
}
else {
return false;
}
}
cur = new Node(kv);
cur->_col = RED;
if (parent->_kv.first < kv.first) {
parent->_right = cur;
}
else {
parent->_left = cur;
}
cur->_parent = parent;
while (parent && parent->_col == RED) {
Node* grandfather = parent->_parent;
if (parent == grandfather->_left) {
Node* uncle = grandfather->_right;
//uncle存在且为红
if (uncle && uncle->_col == RED) {
//变色
parent->_col = uncle->_col = BLACK;
grandfather->_col = RED;
//继续向上处理
cur = grandfather;
parent = cur->_parent;
}
else {//uncle不存在或 存在且为黑
if (cur == parent->_left) {
// g
// p
//c
RotateR(grandfather);
parent->_col = BLACK;
grandfather->_col = RED;
}
else {
// g
// p
// c
RotateL(parent);
RotateR(grandfather);
cur->_col = BLACK;
grandfather->_col = RED;
}
break;
}
}
else {//parent == grandfather->_right
Node* uncle = grandfather->_left;
//uncle存在且为红
if (uncle && uncle->_col == RED)
{
//变色
parent->_col = uncle->_col = BLACK;
grandfather->_col = RED;
//继续向上处理
cur = grandfather;
parent = cur->_parent;
}
else {
if (cur == parent->_right) {
// g
// p
// c
RotateL(grandfather);
grandfather->_col = RED;
parent->_col = BLACK;
}
else {
// g
// p
// c
RotateR(parent);
RotateL(grandfather);
cur->_col = BLACK;
grandfather->_col = RED;
}
break;
}
}
}
_root->_col = BLACK;
return true;
}5. 平衡性检查
红黑树的检测分为两步:
- 1. 检测其是否满足二叉搜索树(中序遍历是否为有序序列)
- 2. 检测其是否满足红黑树的性质
cpp
bool IsBalance()
{
return IsBalance(_root);
}
bool IsBalance(Node* root)
{
if (root == nullptr)
return true;
if (root->_col != BLACK)
{
return false;
}
// 基准值
int benchmark = 0;
Node* cur = _root;
while (cur)
{
if (cur->_col == BLACK)
++benchmark;
cur = cur->_left;
}
return CheckColour(root, 0, benchmark);
}三. RBTree 与 AVLTree 的 比较分析
普通的二叉查找树(BST)在极端情况下(如插入有序数据)会退化成链表,使得操作的时间复杂度变为 O(n)。为了解决这个问题,出现了自平衡二叉查找树,其中最著名的两种是:
-
AVL树:通过严格的平衡因子(左右子树高度差不超过1)来保证绝对的平衡,因此查询效率极高(O(log n))。但在频繁的插入和删除操作中,需要更频繁地进行旋转来维持平衡,效率会受到影响。
-
红黑树:通过不那么严格的平衡规则("近似平衡"),降低了在插入和删除时维持平衡的代价。虽然在查询上可能比AVL树稍慢(因为不如AVL树平衡),但在插入和删除操作更频繁的场景下,整体性能更优。
简单比喻:
-
AVL树:像一位严格的教官,时刻要求队伍绝对整齐,稍有歪斜就立刻调整。
-
红黑树:像一位更务实的经理,允许队伍在一定范围内不那么整齐,以减少频繁调整带来的开销,整体效率更高。
| 特性 | 红黑树 | AVL 树 |
|---|---|---|
| 平衡标准 | 宽松(最长路径 ≤ 2倍最短路径) | 严格(左右子树高度差 ≤ 1) |
| 查询性能 | 平均稍慢于 AVL | 查询更快(因为更平衡) |
| 插入/删除性能 | 更快(需要更少的旋转来维护平衡) | 平均稍慢于红黑树 |
| 应用场景 | 需要频繁插入删除的场景 | 查询频繁,插入删除较少的场景 |
| 例子 | std::map, std::set (C++), Java HashMap |
数据库索引(读多写少) |
简单总结:AVL 树是更严格的"学霸",查询极快但维护成本高;红黑树是"实用主义者",在查询和修改之间取得了很好的平衡。
四. RBTree的递归实现(补充)完整实现
cpp
#pragma once
#include <iostream>
#include <utility>
#include <string>
#include <algorithm>
#include <limits>
// 红黑树核心性质(先明确规则,再看代码如何实现):
// 1. 根节点是黑色;
// 2. 所有叶子节点(空节点)是黑色;
// 3. 红色节点的左、右子节点必须是黑色(无连续红节点);
// 4. 从任意节点到其所有叶子节点的路径,黑节点数量相同(黑高一致);
// 5. 新插入节点默认是红色(避免直接破坏性质4,减少修复工作量)。
// 节点颜色枚举:定义红黑树节点的两种颜色
enum Colour {
RED, // 红色节点
BLACK // 黑色节点
};
// 红黑树节点结构:存储数据、指针和颜色,是树的基本单元
template<class K, class V>
struct RBTreeNode {
RBTreeNode<K, V>* _left; // 左子节点指针
RBTreeNode<K, V>* _right; // 右子节点指针
RBTreeNode<K, V>* _parent; // 父节点指针(递归修复需回溯访问祖先,必须保留)
std::pair<K, V> _kv; // 存储键值对(K为键,需支持比较;V为值)
Colour _col; // 节点颜色
// 构造函数:新节点默认红色(遵循红黑树性质5)
RBTreeNode(const std::pair<K, V>& kv)
: _left(nullptr), // 初始无左子
_right(nullptr), // 初始无右子
_parent(nullptr), // 初始无父节点(后续插入时赋值)
_kv(kv), // 初始化键值对
_col(RED) // 新节点默认红色,减少黑高冲突
{}
};
// 递归实现的红黑树类:核心用递归处理插入/删除,贴合二叉树递归本质
template<class K, class V>
class RBTreeRecursive {
public:
typedef RBTreeNode<K, V> Node; // 简化节点类型名
// 构造函数:初始化空树(根为null,旋转次数为0)
RBTreeRecursive() : _root(nullptr), _rotateCount(0) {}
// 禁止拷贝构造和赋值:避免深拷贝复杂逻辑,防止浅拷贝导致内存问题
RBTreeRecursive(const RBTreeRecursive&) = delete;
RBTreeRecursive& operator=(const RBTreeRecursive&) = delete;
// 析构函数:递归销毁所有节点,释放内存
~RBTreeRecursive() {
_Destroy(_root);
}
// ------------------------------ 对外接口:插入 ------------------------------
// 重载1:单独传入键和值(更易用)
bool Insert(const K& key, const V& value) {
return Insert(std::make_pair(key, value)); // 转为键值对调用重载2
}
// 重载2:传入键值对(核心插入接口)
bool Insert(const std::pair<K, V>& kv) {
bool inserted = false; // 标记是否成功插入(键不存在则成功,存在则更新值)
// 递归插入:返回插入后的根节点,同时更新inserted状态
_root = _InsertRecursive(_root, nullptr, kv, inserted);
// 确保根节点始终为黑色(遵循红黑树性质1,递归修复可能误改根颜色)
if (_root) {
_root->_col = BLACK;
}
return inserted;
}
// ------------------------------ 对外接口:删除 ------------------------------
bool Erase(const K& key) {
bool erased = false; // 标记是否成功删除(键存在则成功,不存在则失败)
// 递归删除:返回删除后的根节点,同时更新erased状态
_root = _RemoveRecursive(_root, key, erased);
// 确保根节点始终为黑色(删除修复可能误改根颜色)
if (_root) {
_root->_col = BLACK;
}
return erased;
}
// ------------------------------ 对外接口:查找 ------------------------------
// 查找键对应的节点(返回指针,可操作值)
Node* Find(const K& key) const {
return _FindRecursive(_root, key); // 递归查找
}
// 判断键是否存在(封装Find,更易用)
bool Contains(const K& key) const {
return Find(key) != nullptr; // 找到则存在,否则不存在
}
// ------------------------------ 对外接口:工具函数 ------------------------------
// 校验红黑树是否平衡(是否满足所有5条性质)
bool IsBalance() const {
return _IsBalance(_root);
}
// 计算树的高度(根到最深叶子的节点数)
int Height() const {
return _Height(_root);
}
// 计算树的节点总数
int Size() const {
return _Size(_root);
}
// ------------------------------ 对外接口:调试函数 ------------------------------
// 打印树结构(右-根-左顺序,直观展示层级)
void PrintTree() const {
std::cout << "红黑树结构:" << std::endl;
_PrintTree(_root, 0); // 初始深度为0
std::cout << std::endl;
}
// 中序遍历(红黑树是有序树,中序遍历结果为键升序)
void InOrder() const {
std::cout << "中序遍历: ";
_InOrder(_root);
std::cout << std::endl;
}
// 获取旋转次数(调试用,观察插入/删除的旋转频率)
int GetRotateCount() const {
return _rotateCount;
}
// 清空树(销毁所有节点,恢复空树状态)
void Clear() {
_Destroy(_root);
_root = nullptr;
_rotateCount = 0;
}
private:
Node* _root; // 树的根节点(整个树的入口)
int _rotateCount; // 统计旋转次数(调试用,无功能意义)
// ==================== 核心模块1:插入相关(递归) ====================
// 递归插入核心:找到插入位置,创建节点,回溯时修复平衡
// 参数:root-当前子树根,parent-当前节点的父节点,kv-待插入键值对,inserted-插入状态
// 返回:插入后当前子树的新根(递归回溯时更新父节点的子指针)
Node* _InsertRecursive(Node* root, Node* parent, const std::pair<K, V>& kv, bool& inserted) {
// 递归终止条件:找到空位置,创建新节点(插入的核心步骤)
if (root == nullptr) {
Node* newNode = new Node(kv); // 新节点默认红色
newNode->_parent = parent; // 绑定父节点(后续修复需用)
inserted = true; // 标记插入成功
return newNode; // 返回新节点,作为父节点的子指针
}
// 1. 递归查找插入位置(按二叉搜索树规则:左小右大)
if (kv.first < root->_kv.first) {
// 键比当前节点小,插入左子树,返回的新左子根更新当前节点的左指针
root->_left = _InsertRecursive(root->_left, root, kv, inserted);
} else if (kv.first > root->_kv.first) {
// 键比当前节点大,插入右子树,返回的新右子根更新当前节点的右指针
root->_right = _InsertRecursive(root->_right, root, kv, inserted);
} else {
// 键已存在:更新值(不插入新节点),标记插入失败
root->_kv.second = kv.second;
inserted = false;
return root; // 返回原节点,无需更新父指针
}
// 2. 回溯阶段:插入后修复红黑树平衡(核心!重点理解)
return _FixInsertion(root);
}
// 插入后平衡修复:处理插入新节点(红)导致的失衡,确保满足红黑树性质
// 参数:node-当前需要修复的节点(递归回溯时的节点)
// 返回:修复后当前子树的新根(用于更新父节点的子指针)
Node* _FixInsertion(Node* node) {
// 修复终止条件:
// 1. 已修复到根节点(根需设为黑,直接返回);
// 2. 当前节点的父节点是黑色(无连续红节点,无需继续修复)
if (node == _root || node->_parent->_col == BLACK) {
if (node == _root) {
node->_col = BLACK; // 确保根为黑(性质1)
}
return node;
}
// 明确三个关键节点:当前节点、父节点、祖父节点(父为红,祖父必存在且为黑)
Node* parent = node->_parent; // 父节点(红色,否则已终止)
Node* grandparent = parent->_parent; // 祖父节点(黑色,因父为红且非根)
// 防御性判断:避免祖父为空(理论上不会触发,因父为红则非根,祖父必存在)
if (grandparent == nullptr) {
return node;
}
// 确定叔叔节点:祖父的另一个子节点(父是左子则叔叔是右子,反之亦然)
Node* uncle = (parent == grandparent->_left) ? grandparent->_right : grandparent->_left;
// ------------------------------ 插入修复场景1:叔叔是红色 ------------------------------
// 场景特点:父红、叔红、祖父黑 → 颜色调整即可,无需旋转
// 原理:将红色节点分散到祖父层,避免连续红,同时保持黑高一致
if (uncle != nullptr && uncle->_col == RED) {
parent->_col = BLACK; // 父节点变黑
uncle->_col = BLACK; // 叔叔节点变黑
grandparent->_col = RED;// 祖父节点变红(将红色上移)
// 祖父变红后,可能与它的父节点冲突,需递归修复祖父节点
return _FixInsertion(grandparent);
}
// ------------------------------ 插入修复场景2:叔叔是黑色(需旋转) ------------------------------
// 场景特点:父红、叔黑、祖父黑 → 需旋转调整结构,再改颜色
// 分4个子场景:LL、LR、RR、RL(按"父在祖父的哪侧"和"当前节点在父的哪侧"判断)
// 子场景1:父是祖父的左子(左支)
if (parent == grandparent->_left) {
// 子子场景1.1:当前节点是父的右子(LR场景)→ 先左旋父,转为LL场景
if (node == parent->_right) {
Node* newParent = _RotateL(parent); // 左旋父节点,返回旋转后的新父(原当前节点)
// 更新祖父节点的左指针:原父节点的位置现在是新父节点
if (grandparent->_left == parent) {
grandparent->_left = newParent;
}
// 重置当前节点和父节点:后续按LL场景处理(新父为原当前节点,当前节点为新父的左子)
node = newParent->_left;
parent = newParent;
}
// 子子场景1.2:当前节点是父的左子(LL场景)→ 右旋祖父,调整颜色
Node* newRoot = _RotateR(grandparent); // 右旋祖父,返回旋转后的新根(原父节点)
parent->_col = BLACK; // 新根(原父)变黑,替代祖父的黑位置
grandparent->_col = RED;// 原祖父变红,避免连续红
return newRoot; // 返回新根,更新上层父指针
}
// 子场景2:父是祖父的右子(右支)
else {
// 子子场景2.1:当前节点是父的左子(RL场景)→ 先右旋父,转为RR场景
if (node == parent->_left) {
Node* newParent = _RotateR(parent); // 右旋父节点,返回旋转后的新父(原当前节点)
// 更新祖父节点的右指针:原父节点的位置现在是新父节点
if (grandparent->_right == parent) {
grandparent->_right = newParent;
}
// 重置当前节点和父节点:后续按RR场景处理
node = newParent->_right;
parent = newParent;
}
// 子子场景2.2:当前节点是父的右子(RR场景)→ 左旋祖父,调整颜色
Node* newRoot = _RotateL(grandparent); // 左旋祖父,返回旋转后的新根(原父节点)
parent->_col = BLACK; // 新根(原父)变黑
grandparent->_col = RED;// 原祖父变红
return newRoot; // 返回新根,更新上层父指针
}
}
// ==================== 核心模块2:删除相关(递归) ====================
// 递归删除核心:找到待删节点,按子节点数量处理,回溯时修复平衡
// 参数:root-当前子树根,key-待删键,erased-删除状态
// 返回:删除后当前子树的新根(更新父节点的子指针)
Node* _RemoveRecursive(Node* root, const K& key, bool& erased) {
// 递归终止条件:未找到待删节点,返回空
if (root == nullptr) {
erased = false;
return nullptr;
}
// 1. 递归查找待删节点(按二叉搜索树规则:左小右大)
if (key < root->_kv.first) {
root->_left = _RemoveRecursive(root->_left, key, erased);
} else if (key > root->_kv.first) {
root->_right = _RemoveRecursive(root->_right, key, erased);
} else {
// 2. 找到待删节点,按子节点数量分3种情况处理
erased = true; // 标记找到待删节点,后续是否删除成功看是否释放节点
// ------------------------------ 删除情况1:叶子节点或只有一个子节点 ------------------------------
// 子情况1.1:无左子 → 用右子替代待删节点
if (root->_left == nullptr) {
Node* rightChild = root->_right; // 右子(可能为空)
bool isBlack = (root->_col == BLACK); // 待删节点是否为黑(黑节点删除会破坏黑高)
delete root; // 释放待删节点内存
// 若待删节点是黑色:需补充黑高(否则违反性质4)
if (isBlack) {
if (rightChild) {
// 右子存在:将右子设为黑(继承待删节点的黑,补充黑高)
rightChild->_col = BLACK;
} else {
// 右子为空:创建虚拟黑节点(标记黑高缺失位置,后续修复)
rightChild = _CreateDummyNode();
}
}
return rightChild; // 返回替代节点,更新上层父指针
}
// 子情况1.2:无右子 → 用左子替代待删节点(逻辑同上)
else if (root->_right == nullptr) {
Node* leftChild = root->_left;
bool isBlack = (root->_col == BLACK);
delete root;
if (isBlack) {
if (leftChild) {
leftChild->_col = BLACK;
} else {
leftChild = _CreateDummyNode();
}
}
return leftChild;
}
// ------------------------------ 删除情况2:有两个子节点(需找替代节点) ------------------------------
// 原理:二叉搜索树中,双子女节点的替代节点是"中序后继"(右子树最小节点)或"中序前驱"(左子树最大节点)
// 选择中序后继:右子树最小节点(无左子,删除时只需处理右子,简化逻辑)
else {
Node* successor = _FindMin(root->_right); // 找右子树最小节点(中序后继)
root->_kv = successor->_kv; // 用后继的键值覆盖待删节点(不改变待删节点的指针和颜色)
// 递归删除中序后继(后继最多有右子,按情况1处理)
root->_right = _RemoveRecursive(root->_right, successor->_kv.first, erased);
// 若后继是黑色:待删节点的位置相当于失去了一个黑节点,需修复平衡
if (successor->_col == BLACK) {
root = _FixDeletion(root);
}
return root; // 返回待删节点(已被后继键值覆盖),无需更新上层指针
}
}
// 3. 回溯阶段:若当前节点是黑色,可能因子节点删除导致黑高缺失,需修复
if (root && root->_col == BLACK) {
root = _FixDeletion(root);
}
return root;
}
// 查找子树最小节点(中序后继的核心:右子树最左节点)
Node* _FindMin(Node* root) const {
// 循环找最左节点(递归也可,循环更高效)
while (root && root->_left) {
root = root->_left;
}
return root;
}
// 删除后平衡修复:处理黑色节点删除导致的黑高缺失,确保满足红黑树性质
// 参数:node-当前需要修复的节点(黑高缺失的节点)
// 返回:修复后当前子树的新根
Node* _FixDeletion(Node* node) {
// 修复终止条件:
// 1. 已修复到根节点(根为黑,直接返回);
// 2. 当前节点是红色(红色可吸收"额外黑",设为黑即可补充黑高)
if (node == _root || node->_col == RED) {
if (node != _root && node->_col == RED) {
node->_col = BLACK; // 红色节点变黑,吸收额外黑,补充黑高
}
// 释放虚拟节点(若当前节点是虚拟节点,修复后无需保留)
if (_IsDummyNode(node)) {
delete node;
return nullptr;
}
return node;
}
// 明确两个关键节点:当前节点(黑高缺失,视为"额外黑")、父节点
Node* parent = node->_parent;
if (parent == nullptr) { // 防御性判断:当前节点无父(仅根,已终止)
return node;
}
// 确定当前节点是父的左子还是右子,进而找到兄弟节点(父的另一个子)
bool isLeftChild = (parent->_left == node);
Node* sibling = isLeftChild ? parent->_right : parent->_left;
// ------------------------------ 删除修复场景1:兄弟是红色 ------------------------------
// 场景特点:当前黑、父任意、兄弟红 → 旋转转为"兄弟黑"的场景
// 原理:兄弟红 → 旋转后兄弟的子节点变为新兄弟(黑),后续按兄弟黑处理
if (sibling && sibling->_col == RED) {
sibling->_col = BLACK; // 兄弟变黑(替代原父的颜色)
parent->_col = RED; // 父变红(避免连续黑)
if (isLeftChild) {
_RotateL(parent); // 当前是左子:左旋父,兄弟的右子变为新兄弟
} else {
_RotateR(parent); // 当前是右子:右旋父,兄弟的左子变为新兄弟
}
// 旋转后新兄弟是原兄弟的子节点(黑),需重新递归修复
return _FixDeletion(node);
}
// ------------------------------ 删除修复场景2:兄弟是黑色 ------------------------------
// 分3个子场景:兄弟双子黑、兄弟左子红、兄弟右子红
// 子场景2.1:兄弟是黑色,且兄弟的两个子节点都是黑色
// 原理:兄弟无红子,无法"借黑",将额外黑上移到父节点
bool leftBlack = (!sibling || !sibling->_left || sibling->_left->_col == BLACK); // 兄弟左子是否黑
bool rightBlack = (!sibling || !sibling->_right || sibling->_right->_col == BLACK); // 兄弟右子是否黑
if (leftBlack && rightBlack) {
if (sibling) {
sibling->_col = RED; // 兄弟变红(减少当前路径黑数,与父节点的额外黑平衡)
}
// 额外黑上移到父节点,递归修复父节点
return _FixDeletion(parent);
}
// 子场景2.2:兄弟是黑色,且至少一个子节点是红色(需旋转借黑)
if (isLeftChild) {
// 当前是左子:兄弟是父的右子
// 子子场景2.2.1:兄弟左子红、右子黑 → 先右旋兄弟,转为"兄弟右子红"
if (sibling && sibling->_left && sibling->_left->_col == RED && rightBlack) {
sibling->_left->_col = BLACK; // 兄弟左子变黑(替代兄弟的黑)
sibling->_col = RED; // 兄弟变红(避免连续黑)
_RotateR(sibling); // 右旋兄弟,兄弟左子变为新兄弟
sibling = parent->_right; // 更新兄弟为新兄弟(原兄弟左子)
}
// 子子场景2.2.2:兄弟右子红 → 左旋父,借兄弟的红子补充黑高
if (sibling) {
sibling->_col = parent->_col; // 兄弟继承父的颜色(保持黑高)
if (sibling->_right) {
sibling->_right->_col = BLACK; // 兄弟右子变黑(补充当前路径黑高)
}
}
parent->_col = BLACK; // 父变黑(避免额外黑上移)
_RotateL(parent); // 左旋父,兄弟变为新父,补充当前路径黑高
} else {
// 当前是右子:兄弟是父的左子(逻辑对称)
// 子子场景2.2.1:兄弟右子红、左子黑 → 先左旋兄弟,转为"兄弟左子红"
if (sibling && sibling->_right && sibling->_right->_col == RED && leftBlack) {
sibling->_right->_col = BLACK;
sibling->_col = RED;
_RotateL(sibling);
sibling = parent->_left;
}
// 子子场景2.2.2:兄弟左子红 → 右旋父,借兄弟的红子补充黑高
if (sibling) {
sibling->_col = parent->_col;
if (sibling->_left) {
sibling->_left->_col = BLACK;
}
}
parent->_col = BLACK;
_RotateR(parent);
}
// 修复后释放虚拟节点(若当前节点是虚拟节点)
if (_IsDummyNode(node)) {
delete node;
return _root;
}
return _root;
}
// ==================== 核心模块3:旋转操作(红黑树平衡的关键) ====================
// 左旋:将父节点的右子变为新根,父节点变为新根的左子(处理RR场景)
// 参数:parent-需要左旋的节点(原父节点)
// 返回:左旋后的新根节点(原父节点的右子)
Node* _RotateL(Node* parent) {
// 防御性判断:父节点为空或无右子,无需旋转
if (parent == nullptr || parent->_right == nullptr) {
return parent;
}
_rotateCount++; // 统计旋转次数(调试用)
// 明确三个关键节点:原父、原父的右子(新根)、原右子的左子(需转移)
Node* cur = parent->_right; // 原父的右子(旋转后成为新根)
Node* cur_left = cur->_left; // 原右子的左子(旋转后成为原父的右子)
// 步骤1:将cur_left转移给parent的右子
parent->_right = cur_left;
if (cur_left) { // 若cur_left非空,更新其父爱指针
cur_left->_parent = parent;
}
// 步骤2:将parent变为cur的左子
cur->_left = parent;
cur->_parent = parent->_parent; // cur继承parent的父节点
parent->_parent = cur; // parent的父节点变为cur
// 步骤3:更新cur的父节点的子指针(若cur的父非空)
if (cur->_parent == nullptr) {
_root = cur; // cur是原根的父节点,说明cur成为新根
} else {
// 判断parent原先是cur父的左子还是右子,更新为cur
if (cur->_parent->_left == parent) {
cur->_parent->_left = cur;
} else {
cur->_parent->_right = cur;
}
}
return cur; // 返回新根,供上层更新子指针
}
// 右旋:将父节点的左子变为新根,父节点变为新根的右子(处理LL场景)
// 参数:parent-需要右旋的节点(原父节点)
// 返回:右旋后的新根节点(原父节点的左子)
Node* _RotateR(Node* parent) {
// 防御性判断:父节点为空或无左子,无需旋转
if (parent == nullptr || parent->_left == nullptr) {
return parent;
}
_rotateCount++; // 统计旋转次数(调试用)
// 明确三个关键节点:原父、原父的左子(新根)、原左子的右子(需转移)
Node* cur = parent->_left; // 原父的左子(旋转后成为新根)
Node* cur_right = cur->_right; // 原左子的右子(旋转后成为原父的左子)
// 步骤1:将cur_right转移给parent的左子
parent->_left = cur_right;
if (cur_right) { // 若cur_right非空,更新其父爱指针
cur_right->_parent = parent;
}
// 步骤2:将parent变为cur的右子
cur->_right = parent;
cur->_parent = parent->_parent; // cur继承parent的父节点
parent->_parent = cur; // parent的父节点变为cur
// 步骤3:更新cur的父节点的子指针(若cur的父非空)
if (cur->_parent == nullptr) {
_root = cur; // cur成为新根
} else {
// 判断parent原先是cur父的左子还是右子,更新为cur
if (cur->_parent->_left == parent) {
cur->_parent->_left = cur;
} else {
cur->_parent->_right = cur;
}
}
return cur; // 返回新根,供上层更新子指针
}
// ==================== 辅助模块:查找、平衡校验、遍历、销毁 ====================
// 递归查找:按二叉搜索树规则找键对应的节点
Node* _FindRecursive(Node* root, const K& key) const {
// 终止条件:未找到或找到目标节点
if (root == nullptr) {
return nullptr;
}
if (key < root->_kv.first) {
return _FindRecursive(root->_left, key); // 键小,找左子树
} else if (key > root->_kv.first) {
return _FindRecursive(root->_right, key); // 键大,找右子树
} else {
return root; // 找到,返回节点指针
}
}
// 平衡校验:总入口,校验所有红黑树性质
bool _IsBalance(Node* root) const {
if (root == nullptr) { // 空树视为平衡
return true;
}
// 校验性质1:根节点是黑色
if (root->_col != BLACK) {
std::cout << "违反性质: 根节点不是黑色" << std::endl;
return false;
}
// 计算基准黑高:取"根到最左叶子的黑节点数"(所有路径需与基准一致)
int benchmark = 0;
Node* cur = root;
while (cur) {
if (cur->_col == BLACK) {
++benchmark;
}
cur = cur->_left;
}
// 校验性质3(无连续红)和性质4(黑高一致)
return _CheckColour(root) && _CheckBlackHeight(root, 0, benchmark);
}
// 校验性质3:无连续红色节点(红节点的父节点不能是红色)
bool _CheckColour(Node* root) const {
if (root == nullptr) { // 空节点无需校验
return true;
}
// 若当前节点是红色,且父节点也是红色 → 违反性质3
if (root->_col == RED && root->_parent && root->_parent->_col == RED) {
std::cout << "违反性质: 连续红色节点 - "
<< root->_parent->_kv.first << " 和 " << root->_kv.first << std::endl;
return false;
}
// 递归校验左、右子树
return _CheckColour(root->_left) && _CheckColour(root->_right);
}
// 校验性质4:所有路径黑高一致(当前路径黑数需等于基准黑高)
bool _CheckBlackHeight(Node* root, int black_num, int benchmark) const {
// 终止条件:到达空叶子节点,判断当前路径黑数是否等于基准
if (root == nullptr) {
if (black_num != benchmark) {
std::cout << "违反性质: 黑高不一致 (当前: " << black_num
<< ", 基准: " << benchmark << ")" << std::endl;
return false;
}
return true;
}
// 若当前节点是黑色,当前路径黑数+1
if (root->_col == BLACK) {
++black_num;
}
// 递归校验左、右子树(左子树和右子树的黑数需都等于基准)
return _CheckBlackHeight(root->_left, black_num, benchmark) &&
_CheckBlackHeight(root->_right, black_num, benchmark);
}
// 计算树高:递归计算(根到最深叶子的节点数)
int _Height(Node* root) const {
if (root == nullptr) { // 空节点高度为0
return 0;
}
// 当前节点高度 = 左子树高度和右子树高度的最大值 + 1(当前节点)
return std::max(_Height(root->_left), _Height(root->_right)) + 1;
}
// 计算节点总数:递归统计(左子树节点数 + 右子树节点数 + 1(当前节点))
int _Size(Node* root) const {
if (root == nullptr) { // 空节点数为0
return 0;
}
return _Size(root->_left) + _Size(root->_right) + 1;
}
// 打印树结构:右-根-左顺序(逆中序),按深度缩进,直观展示层级
void _PrintTree(Node* root, int depth) const {
if (root == nullptr) { // 空节点不打印
return;
}
// 1. 先打印右子树(右子树层级比当前深1)
_PrintTree(root->_right, depth + 1);
// 2. 打印当前节点:缩进(深度*4空格)+ 键+颜色 + 父节点键
std::string color_str = (root->_col == RED) ? "R" : "B"; // 颜色字符串
std::string parent_str = (root->_parent) ?
std::to_string(root->_parent->_kv.first) : "NULL"; // 父节点键(空则为NULL)
std::cout << std::string(depth * 4, ' ')
<< root->_kv.first << color_str
<< "(父:" << parent_str << ")" << std::endl;
// 3. 再打印左子树(左子树层级比当前深1)
_PrintTree(root->_left, depth + 1);
}
// 中序遍历:左-根-右顺序(红黑树是有序树,遍历结果为键升序)
void _InOrder(Node* root) const {
if (root == nullptr) { // 空节点不遍历
return;
}
_InOrder(root->_left); // 1. 遍历左子树
// 2. 遍历当前节点:打印键+颜色
std::cout << root->_kv.first << "(" << (root->_col == RED ? "R" : "B") << ") ";
_InOrder(root->_right); // 3. 遍历右子树
}
// 递归销毁树:后序遍历(左-右-根),避免先删父节点导致子节点内存泄漏
void _Destroy(Node* root) {
if (root == nullptr) { // 空节点无需销毁
return;
}
_Destroy(root->_left); // 1. 销毁左子树
_Destroy(root->_right); // 2. 销毁右子树
delete root; // 3. 销毁当前节点
}
// 创建虚拟节点:删除黑色叶子节点时,标记黑高缺失位置(默认黑色)
Node* _CreateDummyNode() {
// 虚拟节点键值为默认值(后续通过_IsDummyNode判断)
Node* dummy = new Node(std::make_pair(K(), V()));
dummy->_col = BLACK; // 虚拟节点为黑色,补充黑高
// 注意:此处未设置_parent,需在调用处手动赋值(当前代码潜在优化点)
return dummy;
}
// 判断是否为虚拟节点:通过键和值是否为默认值判断(当前代码潜在优化点)
// 优化方向:在Node中添加bool _isDummy成员,避免默认键值误判
bool _IsDummyNode(Node* node) const {
return node->_kv.first == K() && node->_kv.second == V();
}
};结语:感谢相遇
/// 高山仰止,景行行止。虽不能至,心向往之 ///
