文章目录
前言
本文介绍了并查集(Disjoint Set)的优化方法,重点分析了路径压缩技术。通过将查找路径上的所有节点直接挂载到根节点,使树高显著降低。文章详细阐述了压缩路径的实现原理和代码示例,并对比了原始版本、Union优化和Find优化三种方式的时间复杂度:从O(n²)优化到O(nα(n)),其中α(n)是增长极慢的函数。最后提供了可视化工具链接帮助理解算法过程。全文简明扼要地讲解了并查集的核心优化思路------尽可能降低树高,提升查询效率。
代码在文章开头,需要自取🧐
一.拓展:Find操作的优化(压缩路径)
1.查找路径的概念
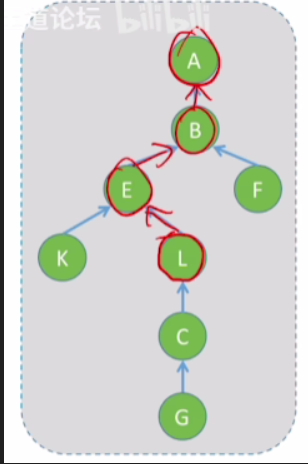
- 对于L这个结点,它从它本身找到根节点的路径叫做查找路径
- 压缩路径的这种优化方式其实就是要使得这个查找路径变短
2.压缩路径的思路
- 压缩路径------ Find 操作,先找到根节点,再将查找路径上所有结点都挂到根结点下
1.具体例子
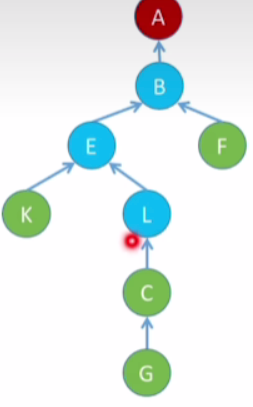

-
把L的查找路径上的这几个蓝色节点,全部都把它们挂到A这个根节点的下面
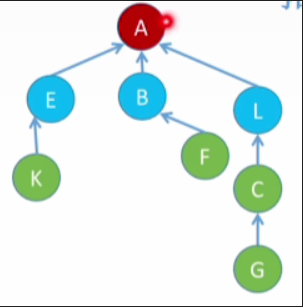

-
那么下一次找这个结点的时候只需走一次就可以找到根结点了
3.压缩路径的代码实现
c
//Find"查"操作优化,先找到根节点,再进行"压缩路径"
int Find(int S[],int x){
int root=x;
while(S[root]>=0) root=S[root]; //循环找到根
while(x!=S[x]; //压缩路径
int t = S[x];//t指向x的父节点
S[x]=root; //x直接挂到根节点下
x=t;
}
return root; //返回根节点编号
}4.优化后的影响
- 每次Find操作,先找根,再"压缩路径",可使树的高度不超过O(α(n))。α(n)是一个增长很缓慢的函数,对于常见的n值,通常α(n)≤4,因此优化后并查集的Find、Union操作时间开销都很低。
二.并查集的优化过程
核心思想:尽可能让树变矮
1.原始版本
- 用数组、双亲表示法来描述元素之间的集合关系。根节点为-1,非根节点指向父节点下标。
- F i n d ( i n t S [ ] , x ) Find (int S[],x) Find(intS[],x)------找到x所属集合 U n i o n ( i n t S [ ] , i n t x , i n t y ) Union(int S[],int x,int y) Union(intS[],intx,inty)------将x、y所属集合合并
- 最坏时间复杂度:
- Find 操作 = 最坏树高 = O(n)
- 将n个独立元素通过多次Union合并为一个集合------ O ( n 2 ) O(n^{2}) O(n2)
2.Union优化
- 用根节点的负值表示一棵树的结点总数
- 每次 Union 操作让小树合并到大树根节点下面
- 最坏时间复杂度:
- Find操作=最坏树高=O(log₂n)
- 将n个独立元素通过多次Union合并为一个集合------O(nlog₂n)
3.Find优化
- "压缩路径"的策略,每次 Find操作先找到x所属根节点,再将查找路径上的所有结点都直接挂在根节点下面
- 最坏时间复杂度:
- Find操作= 最坏树高 = O ( α ( n ) ) O(\alpha(n)) O(α(n))
- 将 n 个独立元素通过多次 Union 合并为一个集合------ O ( n α ( n ) ) O(n\alpha(n)) O(nα(n))
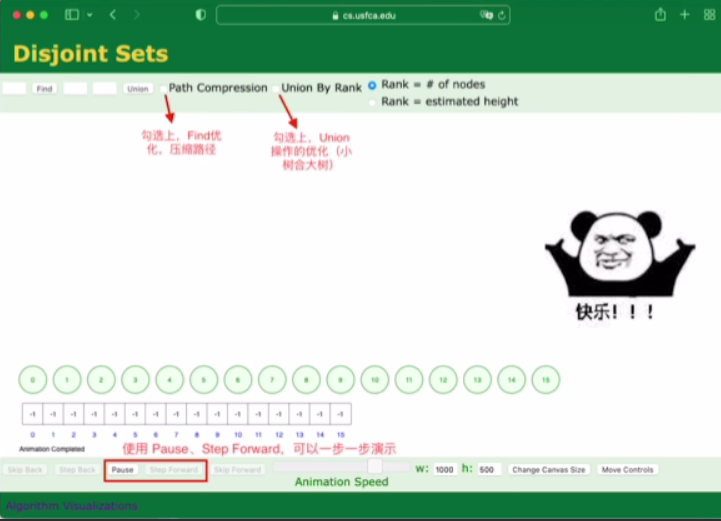
408快乐站(这个网站几乎涵盖了所有大纲要求掌握的算法)
点开链接玩一玩: 408快乐站
结语
这可不是我偷懒啊,王道这一节里面就只有这点内容😖
如果想看更多章节,请点击:一、数据结构专栏导航页