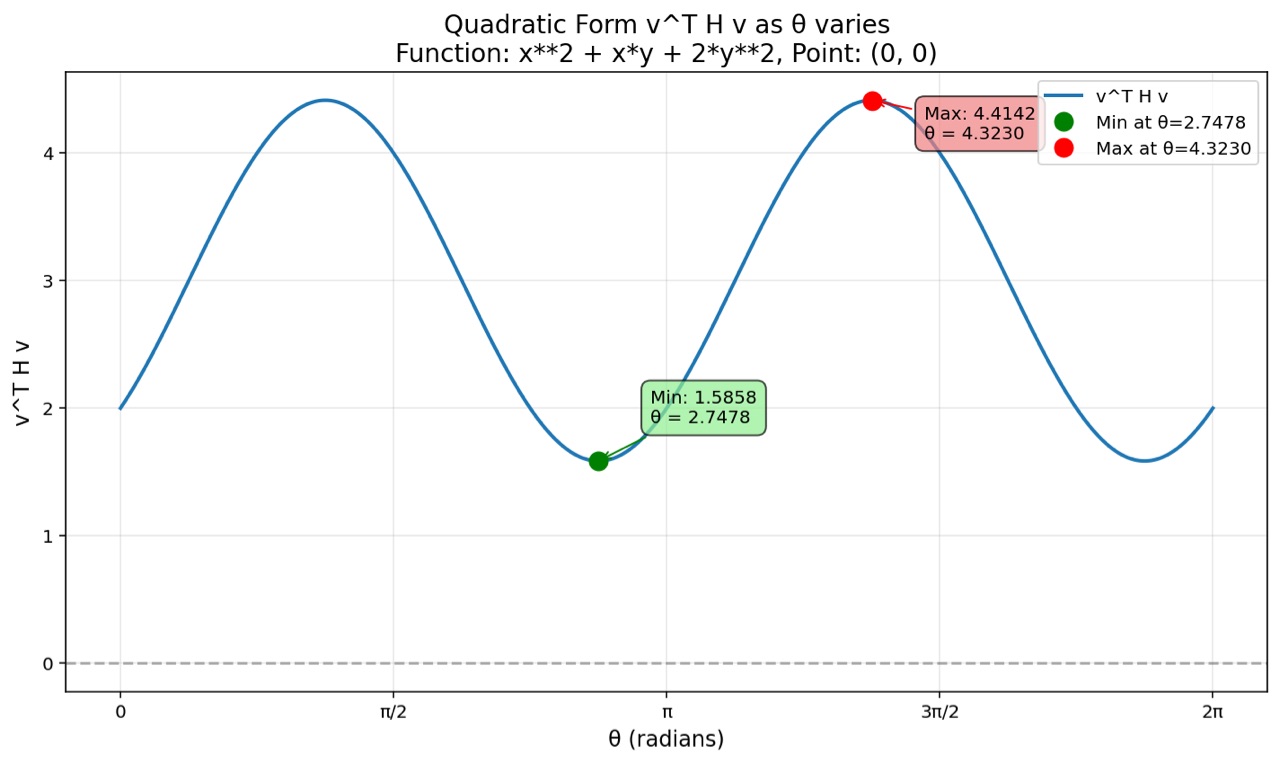
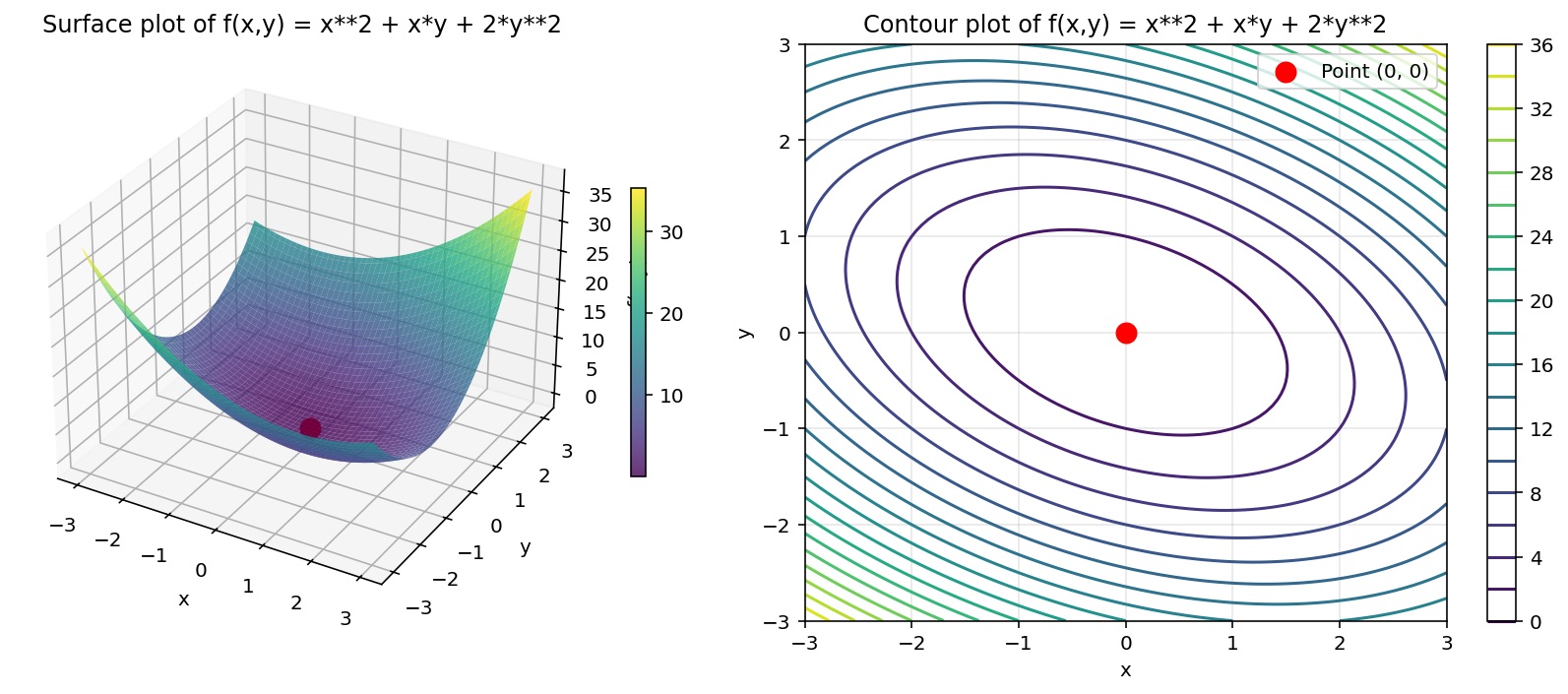
想想刚才发生了什么。我们有一个优化问题:"当 v 旋转时,v^T H v 的最大值和最小值是多少?" 这似乎需要用到微积分,检查所有无穷多个方向......
但事实证明,答案直接通过这个代数方程编码在矩阵本身中!特征值就是那些极端曲率。
更深层次的原因在于:当 v 是一个特征向量,一个特殊的方向时,H·v 不再是把 v 拉向其他方向,而是指向与 v 相同的方向,只是乘以了特征值 λ。
所以:v^T H v = v^T (λv) = λ(v^T v) = λ
因为对于单位向量,v^T v = 1。
所以在特征向量方向上,"曲率"恰好等于特征值。而这些方向恰好是曲率最大和最小的地方!
这不仅仅是我们用来做曲面的 2×2 Hessian 矩阵。这是任意维度上二次优化的基本结构。
当你训练一个包含数百万个参数的神经网络时,Hessian 矩阵就是一个百万乘百万的矩阵。在这个难以理解的高维空间中,你可以问自己:"哪个方向的曲率最陡?哪个方向最平坦?"
特征值会告诉你答案:最大的特征值代表曲率最陡的方向,最小的特征值代表最平坦的谷底。
这就是我们理解优化景观的方式。这就是我们判断梯度下降法是否有效、是否停滞或是否震荡的方式。 Hessian 矩阵的特征值,它们是理解学习几何的诊断工具。
如果你想了解大模型是如何被训练的,这已经接近核心了。Hessian 矩阵、特征值、高维空间中的曲率,这些正是塑造大模型的数学领域。
考试的时候,每个人都机械地计算特征值和特征向量,却不知道为什么。但现我们先明白了为什么,先把曲率形象化了,发现了极值,然后我们再学习计算,这其实是更好的顺序。
对于之前的扁碗的Hessian矩阵:H = [[2,1] [1,4]]
我们找到了特征值:λ₁ = 3 + √2 ≈ 4.414 和 λ₂ = 3 - √2 ≈ 1.586
为了求 λ₁ = 3 + √2 的特征向量,我们求解:
(H - λ₁I)v = 0
\[2-(3+√2), 1 \]\[1, 4-(3+√2) \]\] \[\[v₁\] \[v₂\]\] = \[\[0\] \[0\]
\[-1-√2, 1 \] \[1, 1-√2 \]\] \[\[v₁\] \[v₂\]\] = \[\[0\] \[0\]
从第一行开始:(-1-√2)v₁ + v₂ = 0
所以:v₂ = (1+√2)v₁
我们可以取 v₁ = 1,因此特征向量近似为 (1, 2.414),指向曲率最大的方向。
而根据程序画的正弦曲线,最高点出现在 θ = (4.3230-3.1416)/3.1416 ≈ 0.375 π 的附近。而 tan(0.375 π) ≈ 2.42。