算法原理
滑动窗口
算法思路:
问题分析的对象一般是一段连续的区间
这个窗口寻找的是:以当前窗口最左侧元素(left1)为基准,符合条件的情况找到right,此时是left1的最优解
那么我们就可以大胆的把left1舍去,那么我们left右移,如果让right从头开始必然会有很多重复的计算,我们就可以让right先不动,如果不满足要求,那么right++,则可知left和right是同向移动的,不回退的,所以时间复杂度是O(N)
题目解析
1.长度最小的子数组
https://leetcode.cn/problems/minimum-size-subarray-sum/
题目解析
给定一个含有n个正整数的数组和一个目标t,找出数组中满足和>t的长度最小的连续子数组,返回其长度不存在,返回0
算法原理
解法一:暴力解法 暴力枚举出所有子数组的和
解法二:利用单调性,使用滑动窗口进行优化

代码实现
public int minSubArrayLen(int target, int[] nums) {
int n=nums.length,sum=0;
int len=Integer.MAX_VALUE;
for(int left=0,right=0;right<n;right++){
sum+=nums[right];
while(sum>=target){
len=Math.min(len,right-left+1);
left++;
sum-=nums[left-1];
}
}
return len==Integer.MAX_VALUE?0:len;
}2.无重复字符的最长子串
https://leetcode.cn/problems/longest-substring-without-repeating-characters/description/
题目解析
给定一个字符串s,请你找出不含重复字符的最长子串的长度
算法原理
解法一:暴力枚举+哈希表(哈希表可以发现重复字符)
解法二:滑动窗口
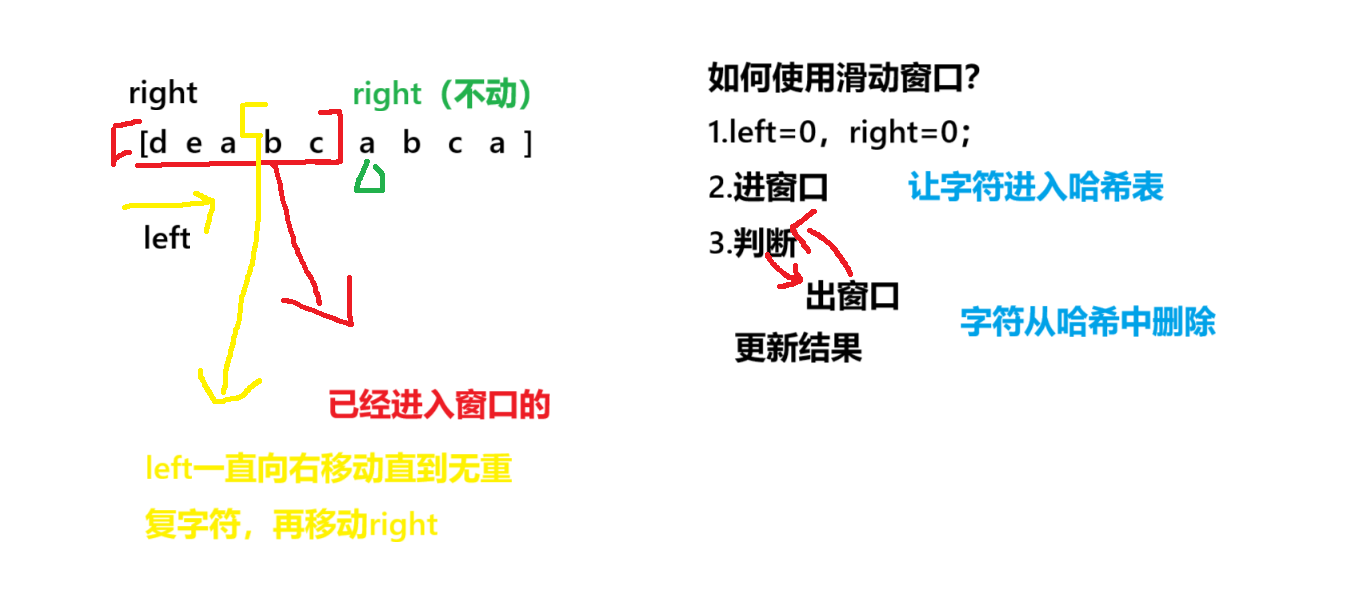
代码实现
class Solution {
public int lengthOfLongestSubstring(String ss) {
char[] s=ss.toCharArray();
int[] hash=new int[128];
int left=0,right=0,n=ss.length(),ret=0;
while(right<n){
hash[s[right]]++;
while(hash[s[right]]>1){
hash[s[left++]]--;
}
ret=Math.max(ret,right-left+1);
right++;
}
return ret;
}
}3.最大连续一的个数
https://leetcode.cn/problems/max-consecutive-ones-iii/description/
题目解析
给定一个二进制数组nums和一个整数k,如果最多可以翻转k个0,则返回数组中连续1的最大个数
(最多可以不一定刚好1个)

算法原理
翻转<->找到连续区域的0不超过k个
解法一:暴力解法 固定起点,进行枚举+zero计数器
解法二:滑动窗口
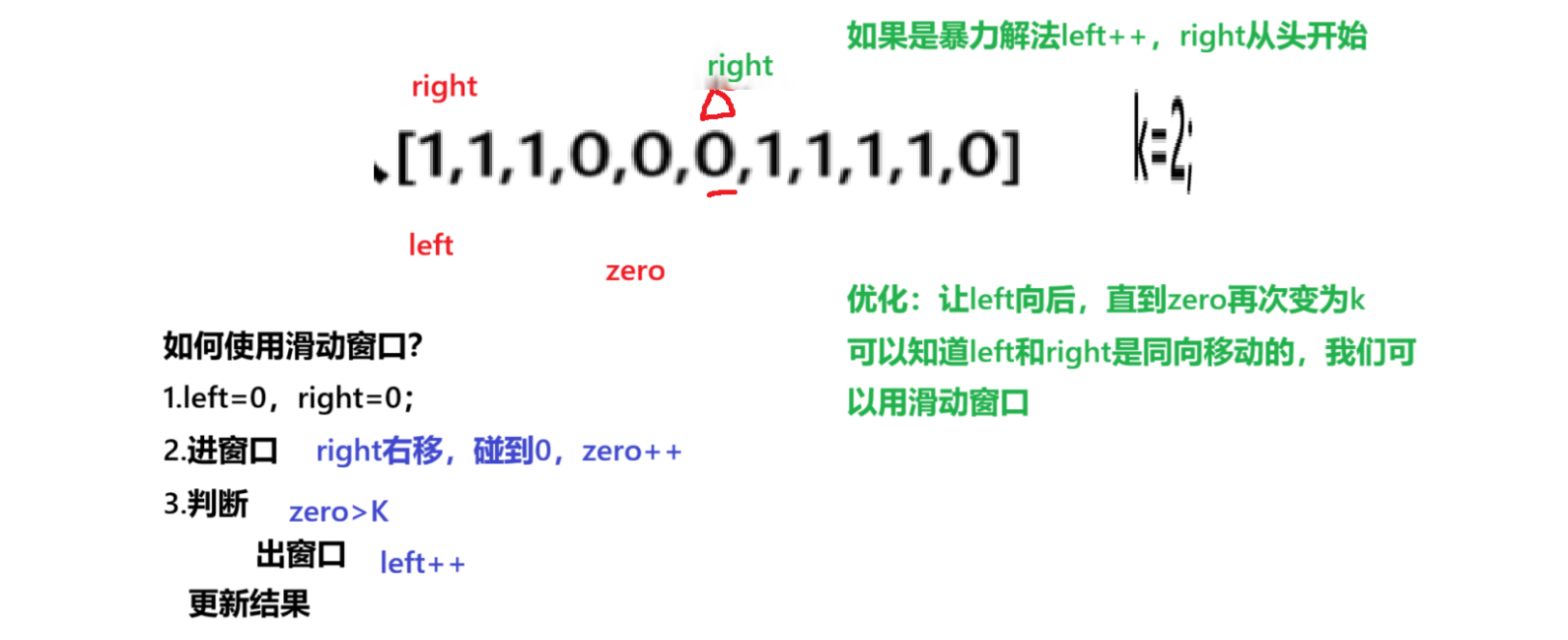
代码实现
class Solution {
public int longestOnes(int[] nums, int k) {
int n=nums.length,ret=0;
for(int left=0,right=0,zero=0;right<n;right++){
if(nums[right]==0){
zero++;
}
while(zero>k){
if(nums[left]==0){
zero--;
}
left++;
}
ret=Math.max(ret,right-left+1);
}
return ret;
}
}4.将x减到0的最小操作数
题目解析
给定一个nums数组和x,每次应移除nums最左或最右的值,然后从x中减去该元素的值,需要修改数组以供接下来使用,如果可以恰好减到0,返回最小操作数,否则返回-1;
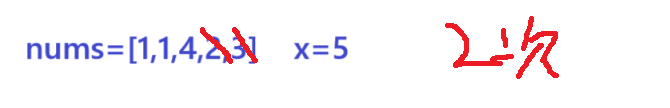
算法原理
如果直接按照题目要求操作会有点难,所以我们将换一种思路

解法一:暴力解法
解法二:滑动窗口
1.left=0,right=0
2.进窗口 tmp+=nums【right】
3.判断 tmp>sum-x;
出窗口 tmp-=nums[left]
更新结果 tmp==sum-t
代码实现
class Solution {
public int minOperations(int[] nums, int x) {
int sum=0;
for(int a:nums){
sum+=a;
}
int t=sum-x;
if(t<0){
return -1;
}
int ret=-1;
for(int left=0,right=0,tmp=0;right<nums.length;right++){
tmp+=nums[right];
while(tmp>t){
tmp-=nums[left++];
}
if(tmp==t){
ret=Math.max(ret,right-left+1);
}
}
if(ret==-1){
return -1;
}else{
return nums.length-ret;
}
}
}