第73题 矩阵置零

题目

给定一个 mxn 的矩阵，如果一个元素为 0 ，则将其所在行和列的所有元素都设为 0 。请使用 原地 算法**。**

示例 1：

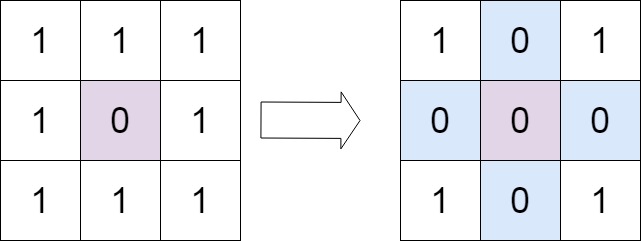
输入：matrix = [[1,1,1],[1,0,1],[1,1,1]]
输出：[[1,0,1],[0,0,0],[1,0,1]]

示例 2：

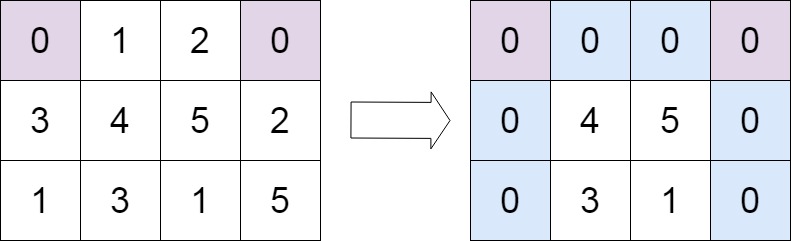
输入：matrix = [[0,1,2,0],[3,4,5,2],[1,3,1,5]]
输出：[[0,0,0,0],[0,4,5,0],[0,3,1,0]]

提示：

• m == matrix.length
• n == matrix[0].length
• 1 <= m, n <= 200
• -231 <= matrix[i][j] <= 231 - 1

思路

创建两个set集合用来记录矩阵中值为零的行数 h 集合和列数 l 集合

遍历整个矩阵找到值为零的数把行数和列数分别添加到两个set集合中

遍历行数 h 集合,把这些行数的所有列的值置为0

遍历列数 l 集合,把这些列数的所有行的值置为0

代码示例

import java.util.*;
public class lc73 {
    public static void main(String[] args) {
        int[][] matrix = {{0,1,2,0}, {3,4,5,2}, {1,3,1,5}};
        lc73 lc73 = new lc73();
        lc73.setZeroes(matrix);
        for (int i = 0; i < matrix.length; i++) {
            System.out.println(Arrays.toString(matrix[i]));
        }
    }
    public void setZeroes(int[][] matrix) {
        //创建两个set集合用来记录矩阵中值为零的行数 h 集合和列数 l 集合
        Set<Integer> h = new HashSet<>();
        Set<Integer> l = new HashSet<>();
        //遍历整个矩阵找到值为零的数把行数和列数分别添加到两个set集合中
        for (int i = 0; i < matrix.length; i++) {
            for (int j = 0; j < matrix[0].length; j++) {
                if(matrix[i][j]==0){
                    h.add(i);
                    l.add(j);
                }
            }
        }
        //遍历行数 h 集合,把这些行数的所有列的值置为0
        for (Integer val : h) {
            for (int i = 0; i < matrix[0].length; i++) {
                matrix[val][i] = 0;
            }
        }
        //遍历列数 l 集合,把这些列数的所有行的值置为0
        for (int i = 0; i < matrix.length; i++) {
            for (Integer val : l) {
                matrix[i][val] = 0;
            }
        }
    }
}