【C++】哈希表详解(开放定址法+哈希桶)

一匹电信狗2025-11-06 11:56

哈希表详解

哈希表详解

github地址

有梦想的电信狗

前言

哈希表（Hash Table）是高效数据查找的核心结构之一，广泛应用于编译器、数据库、系统索引等场景。

它通过哈希函数将关键字直接映射到存储位置，实现平均 O(1) 的插入、查找与删除效率。

本文将从原理 → 冲突处理 → 哈希函数设计 → C++ 实现 → 性能对比 等角度，系统讲解哈希表的完整构造过程，涵盖开放定址法 与**链地址法(哈希桶)**两种典型方案。

阅读完后，你将不仅能使用 STL 的 unordered_map，更能亲手实现一个可运行的通用哈希表。

一、什么是哈希

  • 顺序结构 以及平衡树 中，元素关键码与其存储位置之间没有对应的关系，因此在查找一个元素时，必须要经过关键码的多次比较。

  • 顺序查找 时间复杂度为 O ( N ) O(N) O(N)，平衡树中为树的高度 O( l o g 2 N log_2 N log2N)，搜索的效率取决于搜索过程中元素的比较次数

理想的搜索方法：可以不经过任何比较，一次直接从表中得到要搜索的元素。

  • 如果构造一种存储结构 ，通过某种函数 (hashFunction)使**元素的存储位置与它的关键码之间能够建立一一映射的关系**，那么在查找时通过该函数可以很快找到该元素。

当向该结构中：

  • 插入元素 ：根据待插入元素的关键码，以此函数计算出该元素的存储位置并按此位置进行存放
  • 搜索元素 ：对元素的关键码进行同样的计算，把求得的函数值当做元素的存储位置，在结构中按此位置取元素比较，若关键码相等，则搜索成功

以上方法即为哈希（散列）方法。

哈希（Hash）又称为散列 ：是一种将任意长度的输入数据（通常称为 "键" 或 "关键字"）通过特定的数学算法（称为 "哈希函数"）映射为固定长度输出的技术。

  • 本质 ：通过某种函数把关键字 key 跟它的存储位置建立一个映射关 系，查找时通过这个函数计算出 key 存储的位置，进行快速查找

    • 哈希方法中使用的转换函数 称为哈希（散列）函数，构造出来的数据结构 称为哈希表(Hash Table) (或者称散列表)
    • 哈希函数的输出值被称为 "哈希值"、"散列值" 或 "哈希码"。

  • 哈希的核心目的是快速实现数据的查找、存储和比较 ，广泛应用于哈希表、密码学、数据校验等领域。

二、哈希的样例

哈希样例1：

例如：数据集合{1，7，6，4，5，9}

  • 哈希函数 设置为：hash(key) = key % capacity
    • capacity为存储元素底层空间总的大小
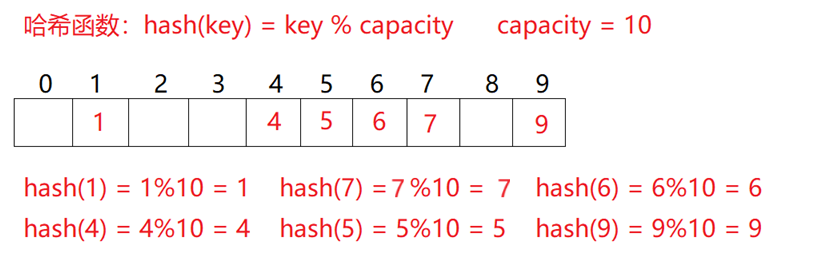
  • 元素存储在下标为元素值的位置上 ，用该方法进行搜索不必进行多次关键码的比较，因此搜索的速度比较快

哈希样例2：

例如：在一个数组中存储英文字母 a，a 的 ascii 码值为 97 ，那么可以把它存储在数组下标为 97 的位置上 。这样一来我们**存储的数据就和数组的下标就建立了一个映射关系，查找数据时就可以直接根据 ascii 码值来查找**。

注：我们将关键字映射到数组中位置，一般是整数才好做映射计算，如果不是整数，我们要想办法转换成整数，这个细节我们后面代码实现中再进行细节展示。

三、哈希冲突

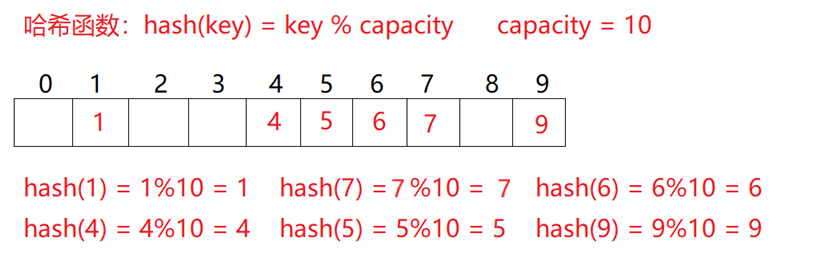
问题：按照上述哈希函数，向集合中插入元素44，会出现什么问题

  • 会出现 元素4 和 元素44 映射到了同一个位置 ，这种情况被称为哈希冲突

哈希冲突（Hash Collision） ：是哈希表设计与实现中无法避免的核心问题，指不同的关键字通过哈希函数计算后，得到相同的哈希地址 的情况。（即：映射到哈希表的同一个桶或位置）

  • 定义 ：于两个不同的关键字 key1 ≠ key2，若它们的哈希值 满足 h(key1）= h(key2），则称这两个关键字发生了哈希冲突。
  • 本质 ：哈希函数是"多对一"的映射（输入空间无限，输出空间有限），根据鸽巢原理，冲突必然存在

产生冲突的原因：

  • 哈希函数的"压缩映射"特性 ：
    • 哈希函数将任意长度的输入 (如：字符串、整数、对象）映射到固定长度的哈希值 (如：size_t类型)
    • 再通过取模等操作 映射到哈希表的桶索引，这种"压缩"必然导致不同输入映射到同一输出
  • 哈希表容量与关键字分布 ：
    • 哈希表容量 m 过小，或关键字分布集中（如大量关键字的哈希值在同一区间），冲突概率会急剧上升
      • 示例：哈希表容量(m == 10)，若所有关键字的哈希值取模后都为 5，则所有数据会冲突到第5个桶

四、哈希函数

1. 哈希函数的定义

哈希函数（HashFunction） ：是哈希表（Hash Table）的核心组成部分。

  • 它的作用是将任意长度的输入数据 （称为"键"或"关键字"）映射到一个固定长度的输出值(称为"哈希值"或"散列值")
  • 这个输出值通常用于确定该键在哈希表中的存储位置。

2. 哈希函数的特点

哈希函数的核心特点：

  • 确定性 ：同一输入必须始终映射到同一个哈希值。
  • 压缩性 ：无论输入数据的长度如何，输出的哈希值长度是固定的。
  • 高效性 ：计算哈希值的过程应快速且易于实现 ，时间复杂度通常为O(1)或 O(k)（k为输入数据的长度），避免成为哈希表操作的性能瓶颈。

3. 哈希函数的设计原则

哈希函数的设计原则：

  • 均匀分布 ：理想情况下，哈希函数应将不同的键均匀地映射到哈希表的各个位置 ，避免大量键集中在少数位置（称为"哈希冲突")
    • 均匀分布能保证哈希表的操作(插入、查找、删除）效率接近O(1)
  • 减少冲突 ：由于输入空间（可能的键）远大于输出空间（哈希表长度），哈希冲突无法完全避免 ，但好的哈希函数能最大限度降低冲突概率

4. 常见的哈希函数

1. 直接定址法(常用)

直接定址法 ：通过直接利用关键字本身 或关键字的某个线性函数 来确定哈希地址，从而实现关键字到存储位置的映射。

  • 直接定址法 是一种简单直观的哈希函数构造方法。

直接定址法的常用哈希函数 ：H(key) = key 或 H(key) = a * key + b

  • key：是待映射的关键字。(需要存储的数据的标识)
  • a 和 b ：是常数。(a ≠ 0，用于对关键字进行线性变换)
  • H(key） ：是计算得到的哈希地址。(即：数据在哈希表中的存储位置)

优缺点与适用场景：

  • 优点：

    • 简单高效 ：无需复杂计算，直接通过关键字映射地址，时间复杂度为 O ( 1 ) O(1) O(1)
    • 无冲突 ：只要关键字不重复，计算出的哈希地址唯一 (因为是线性映射，不存在不同关键字映射到同一地址的情况)

  • 缺点：

    • 空间浪费大 ：如果关键字的范围很大（例如：key 是 1000 到 1000000 的整数），哈希表需要开辟对应范围的空间，但实际存储的关键字可能很少，导致大量空间闲置
    • 关键字需为整型 ：该方法的哈希函数是将关键字 key 经过数学运算，因此若关键字是字符串、浮点数等非整型，需先转换为整型才能使用

  • 适用场景：

    • 关键字的范围较小且连续(或分布集中)
    • 关键字可以直接作为地址(或通过简单线性变换后作为地址)

直接定址法的实际使用案例：

  • 存储学生的年龄（范围通常在5-25 岁），可直接用 H(age）= age，哈希表大小只需 30 左右
  • 存储月份（1-12月），可用H(month）= month，哈希表大小为 12 即可

2. 除法散列法(除留余数法)

除法散列法 ：核心逻辑是用关键字对一个整数取余，把大范围的关键字映射到哈希表的有效下标区间，以此确定存储位置。

  • 除法散列法是哈希函数构造方法里的经典手段。

除留余数法的常用哈希函数 ：H(key) = key % m

  • key：是待映射的关键字。(可以是整数、字符串经转换后的哈希值等)
  • m ：哈希表的大小。 (通常是数组长度，决定了哈希地址的范围)
  • H(key) ：是计算得到的哈希地址。(即：数据在哈希表中的存储下标)

本质 ：利用取余运算的**"截断"特性，把任意 整数** key 映射到 [0，m - 1]区间，让关键字适配哈希表的下标范围

优缺点与适用场景：

  • 优点 ：
    • 实现简单：一行取余运算即可完成映射，编码成本极低
    • 适用性广：只要能转成整数(或本身是整数）的关键字都能用，涵盖整数、字符串、自定义类型(需先哈希转整数)
    • 控制范围 ：通过调整 m 灵活控制哈希地址范围，适配不同内存、性能需求
  • 缺点 ：
    • 冲突概率与 m 强相关 ：若 m 选得不好（比如：是关键字的公约数），会导致大量冲突
      • 例如：关键字都是偶数、m == 4，则哈希地址只能是0，1，2，冲突概率飙升
    • 依赖 m 的选取 ：m 若为合数（尤其是2的幂），易让哈希地址分布不均 （比如：二进制低位相同的关键字会扎堆)
    • 不适用于动态扩容：哈希表扩容后 m 改变，所有关键字需重新计算哈希地址，迁移成本高
  • 适用场景 ：值的分布范围分散

优化 m 的选取：

除法散列法的效果高度依赖 m 的选择，工程中常用以下策略优化

优化策略一：选质数

优先选质数作为 m 的值，能大幅降低冲突概率。原因是：质数的约数少，关键字取余后分布更均匀

  • 正例 ：若 m == 11（质数），关键字10、20、30会映射到0、9、8，分布更分散
  • 反例 ：若 m == 10（合数），上述关键字都会映射到0，冲突严重

优化策略二：避免 m == 2 x 2^x 2x 或 m == 1 0 x 10^x 10x

若 m == 2 x 2^x 2x，key % m 等价于 "保留key的最后 X 位二进制数" 。此时，只要不同key的最后 X 位二进制数相同，哈希值就会冲突。

  • 取 m == 16（即 2 4 2^4 24），计算63 % 16和 31 % 16:
    • 63的二进制后 8 位是 00111111 ，取最后 4 位 1111 →余数 15
    • 31的二进制后 8 位是 00011111 ，取最后 4 位 1111 →余数 15

若 m == 1 0 x 10^x 10x，key % m 等价于 "保留key的最后 X 位十进制数" 。此时，只要不同key的最后 X 位十进制数相同，哈希值就会冲突。

  • 取m == 100（即 1 0 2 10^2 102），计算112 % 100和 12312 % 100:
  • 两者最后 2 位都是12→余数均为 12，哈希值冲突

优化策略三：结合关键字分布调整

若已知关键字的分布（如：都是奇数、或集中在某个区间），选 m 时尽量让余数覆盖更全。

  • 关键字全是奇数，m 选奇数可避免 "余数全为奇数 / 偶数" 的极端情况。

3. 乘法散列法

乘法散列法：

  • 将关键字 key 与一个在(0, 1)之间的常数 A 相乘，得到的结果会是一个小数
  • 这个小数的小数部分，再乘以哈希表的大小 m
  • 最后对结果向下取整，就得到了哈希值

关键特性与优缺点：

  • 优点 ：
    • 哈希值分布均匀 ：当常数 A 选择合适时，乘法散列法 能让哈希值在哈希表中较为均匀地分布，减少哈希冲突的发生。这是因
      为乘法运算能充分打乱关键字的二进制位，使得不同关键字映射到相同哈希值的概率降低。
    • 对哈希表大小要求不严格 ：不像除法散列法对哈希表大小 m 的取值有较多限制（如：尽量取质数等），乘法散列法对 m 的取值
      相对自由，m 可以是任意正整数。
    • 计算效率较高：乘法散列法主要涉及乘法、取小数部分和取整操作，在现代计算机硬件上，这些操作都能高效执行。
  • 缺点 ：
    • 常数 A 的选择有难度：虽然理论上常数 A 只要在(0, 1)之间且为无理数 就能工作，但要找到一个能在实际应用中让哈希值
      分布最优的 A 并不容易，往往需要通过实验和对数据特征的了解来确定。
    • 实现相对复杂：相较于简单的除法散列法，乘法散列法的计算步骤更多，实现代码也相对复杂一些。

使用乘法散列法计算哈希值步骤示例：

假设要对整数关键字 key = 12345 进行哈希计算，哈希表大小 m = 100，常数 A 取黄金分割数 5 − 1 2 \frac{\sqrt{5}-1}{2} 25 −1，计算过程如下:

  1. 计算 key * A : 12345 * 5 − 1 2 \frac{\sqrt{5}-1}{2} 25 −1 ≈ 12345 * 0.6180339887 = 7625.08749
  2. 取小数部分 ：7625.08749 mod 1 = 0.08749
  3. 乘以哈希表大小：0.08749*100 = 8.749
  4. 向下取整得到哈希值：[8.749」= 8

4. 全域散列法

五、负载因子

1. 什么是负载因子

负载因子 ：是哈希表设计与性能分析中的核心概念，用于衡量哈希表的"填充程度" ，直接影响哈希冲突概率和内存利用率

负载因子的定义 ：哈希表中已存储的元素数量 / 哈希表的总容量(或桶的数量)

计算公式 ：load_factor = n/m

  • n ：是哈希表中当前存储的有效元素数量
  • m ：是哈希表的总容量 (即桶数组的长度，如：vector<Node*>的大小

2. 负载因子对哈希表性能的影响

负载因子是哈希冲突概率和内存利用率的"平衡器"，核心影响如下

（1）负载因子越小 → 哈希冲突概率越低

  • load_factor很小时，哈希表很空，每个桶的平均元素数少，链表或探测链短 ，插入、查找、删除的时间复杂度接近 O ( 1 ) O(1) O(1)

  • 但内存浪费严重（大量桶闲置），空间利用率低。

（2）负载因子越大→哈希冲突概率越高

  • load_factor很大时，哈希表快满，链表／探测链长 ，操作时间复杂度会退化到 O ( N ) O(N) O(N)（极端情况哈希表退化为链表)
  • 内存利用率高，但性能会暴跌

因此需要控制负载因子的值，在空间利用率和冲突率之间进行平衡

3. 负载因子超过國值时会发什么？

负载因子驱动扩容 ：哈希表不能满了再进行扩容，控制负载因子到一定值就进行扩容

当负载因子超过阈值时，哈希表需要进行扩容（Resize），流程如下:

  1. 新建更大的桶数组：新容量通常是原容量的 2 倍(或接近的质数，依实现而定)
  2. 重新映射所有元素：遍历旧哈希表的所有元素，用新哈希函数（或新容量重新取模）将元素插入新桶
  3. 释放旧内存：销毁旧桶数组，替换为新桶数组

六、哈希冲突的解决

1. 开放定址法(闭散列法)

开放定址法（OpenAddressing） ：开放定址法是处理哈希冲突的一种系统化方法，所有元素都存储在哈希表数组本身中，通过探测序列寻找可用的空槽位。

  • 它的核心思路 是：当发生哈希冲突时，按照预定的探测规则 在哈希表中找下一个空闲位置 来存储冲突的元素。

原理分析：

  1. 设哈希表的大小为 m ，哈希函数为 h(key)，当通过哈希函数计算出的地址 h(key) 已经被占用，即发生冲突时：
  2. 开放定址法 会使用一个探测序列 h_i(key)（i = 0, 1, 2, ···）来寻找下一个空闲位置，直到找到可以插入的位置或者确定哈希表已满
  3. 探测序列的计算方式决定了开放定址法的具体类型

线性探测

线性探测（LinearProbing）：

  • 探测公式 ：h_i(key)= (h(key）+ i) % m，其中 i = 0, 1, 2, ...
    • 即：在发生冲突时，从发生冲突的位置开始，依次向后探测，直到寻找到下一个空位置为止 (如果到达表尾则回到表头)

示例：

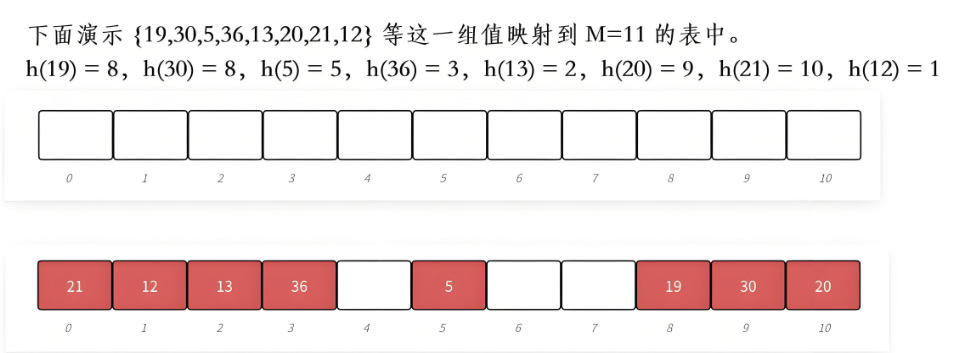
缺点：容易产生 "聚集"（或叫 "堆积"）现象。

  • 即连续的若干个位置被占用，导致后续插入元素时需要探测多个位置，降低插入和查找效率。

2. 链地址法(开散列法)

链地址法 （SeparateChaining）(也叫拉链法 、哈希桶法）：是哈希表解决哈希冲突的经典方案之一。

  • 它的核心思路是：用数组 + 链表 (或其他动态结构）的组合，让冲突元素"链"在一起，既简单又高效。

链地址法的原理：

  • 链地址法哈希表 底层是一个数组 （称为"哈希桶数组"），每个数组元素 对应一个链表／动态结构

插入元素时：

  • 通过哈希函数 计算 key 的哈希值，确定要放入数组的哪个"桶"（即：数组索引)
  • 若该桶对应的链表为空，直接插入
  • 若已存在元素（发生冲突），就进行头插 ，把新元素链入到桶中

查找/删除元素时：

  • 先通过哈希函数找到对应桶
  • 再遍历链表 逐个匹配 key

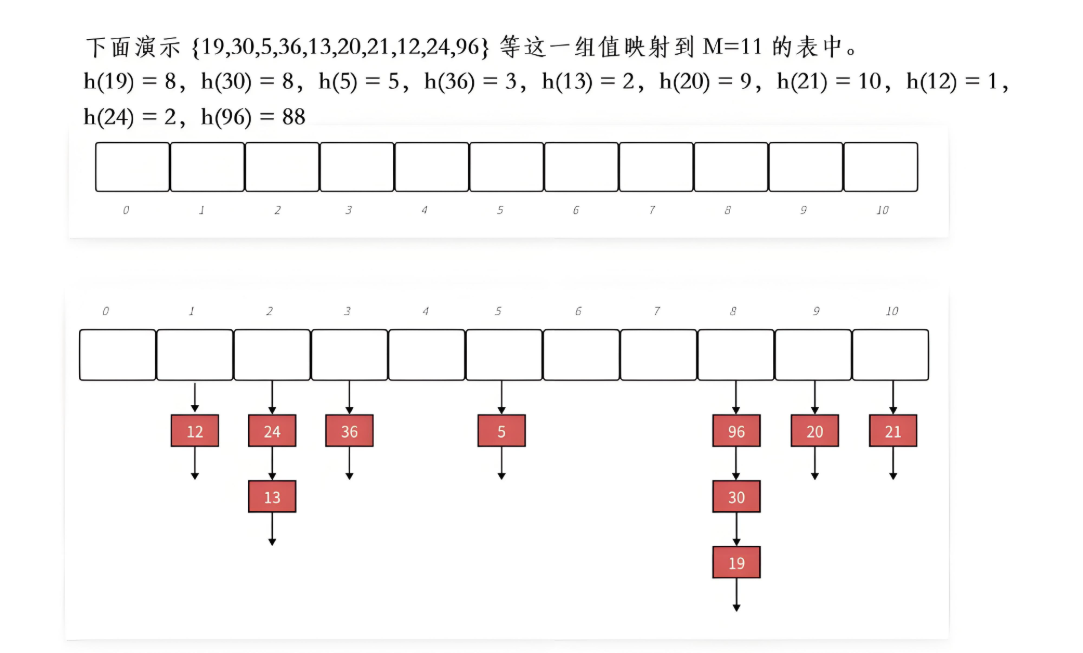
优缺点分析：

优点：

  1. 冲突处理简单：不管冲突多频繁，只需往链表追加，逻辑清晰易实现
  2. 空间灵活：链表是动态结构，负载因子（负载因子 = 元素数 / 桶数 ）可大于 1 ，空间利用率高
  3. 无聚集问题：每个桶的冲突是独立链表，不会像开放定址法那样 "连累" 其他桶

缺点：

  1. 遍历开销：若某个桶的链表过长，查找 / 删除会退化为 O(n)（n 是链表长度 ）
  2. 额外空间：链表节点需要存储指针，有一定内存开销

七、开放定址法 代码实现

在实践里，开放定址法的表现不如链地址法。

  • 原因在于，开放定址法 不管采用哪种冲突解决方式，都是占用哈希表自身的空间 ，这就使得各元素的存储始终存在相互影响的问题。

  • 所以，对于开放定址法 ，我们简单选用线性探测的方式来实现即可 。

1. 哈希结构

结点状态与结点数据类型

cpp 复制代码 
// 哈希表中每个位置的状态
enum STATE
{
	EXIST,
	EMPTY,
	DELETE
};

// 哈希存储的数据
template<class K, class V>
struct HashData
{
	std::pair<K, V> _kv;
	enum STATE _state = EMPTY;
};

enum State ：定义哈希表中节点的三种状态的"枚举"

  • EXIST：存在状态
  • EMPTY,：空状态
  • DELETE：已删除状态

哈希节点结点数据类型：

  • 存储键值对类型，方便映射 ：std::pair<K, V> _kv
  • 结点中存储当前结点的状态，初始值为EMPTY ：enum STATE _state = EMPTY;

哈希表结构设计

cpp 复制代码 
// 哈希表的结构
template<class K, class V, class HashFunc = DefaultHashFunc<K>>		// 默认使用整型的哈希函数
class HashTable
{
private:
	vector<HashData<K, V>> _table;
	size_t _n = 0;  // 存储的有效数据的个数   哈希是分散存储的，vector 是连续存储的，因此即使 vector 提供了 size 接口,也需要这个 _n

public:
    // ... 相关成员函数实现
	HashTable()
	{
		_table.resize(10);
	}
}
  • 哈希表定义为模板实现 ：模板参数设置为template<class K, class V, class HashFunc = DefaultHashFunc<K>>，设置pair中存储的数据K、V类型，并设置默认的哈希函数，同时支持传入自定义的哈希函数
  • 使用 vector 作为表结构：由于 vector 为自定义类型，HashTable 的默认构造函数会自动调用 vector 的 默认构造函数
  • size_t _n = 0：存储有效数据的个数 ，哈希是分散存储的，vector 是连续存储的 ，_n 成员记录表中的有效结点个数，通过比较 _n 和 vector.size() 的大小判断哈希表是否需要扩容
  • 构造函数初始化哈希表 size 为 10

2. 哈希函数设计

开放定址法 采用对关键字取模 来确定其存储位置，这种方法仅适用于可以进行取模运算的类型 ，而字符串也经常做哈希表中的Key，因此我们需要解决字符串不能取模的问题

  • 我们使用仿函数来控制指字符串的取模问题

常用的字符串哈希算法 ：字符串哈希算法

各自使用单独的仿函数设计

cpp 复制代码 
// 使用仿函数控制 string 和 其他整型的取模
template<class K>
struct DefaultHashFunc
{
	size_t operator()(const K& key)
	{
		return static_cast<size_t> (key);
	}
};


struct StringHashFunc
{
    size_t operator()(const string& str)
    {
        // BKDR
        size_t hash = 0;
        for (auto ch : str) {
            hash *= 131;
            hash += ch;
        }
        return hash;
    }
};

// 哈希表模板参数控制
template<class K, class V, class HashFunc = DefaultHashFunc<K>>
class class HashTable
{}

各自使用单独的仿函数设计 ：设计两个单独的仿函数，重载operator()，通过哈希表的模板参数来控制取模运算

  • 默认哈希函数 ：DefaultHashFunc，默认关键字key为可取模的整型，直接返回整型，可以进行取模操作
  • 字符串的哈希函数 ： StringHashFunc：同样是返回一个整数，对字符串进行 BKDR 算法后，尽可能确保不同字符串的哈希值不同
    • 使用该方法设计出的哈希表，在使用时需要显式传入 string的哈希函数HashTable<string, string, StringHashFunc> dict;但 STL 的使用并不需要传入哈希函数 ，接下来介绍使用模板及其特化解决该问题

使用模板及模板特化设计

  • STL 设计的使用并不需要传入哈希函数 ，下面介绍使用模板及其特化解决该问题
cpp 复制代码 
// 使用仿函数控制 string 和 其他整型的取模
template<class K>
struct DefaultHashFunc
{
	size_t operator()(const K& key)
	{
		return static_cast<size_t> (key);
	}
};

// 默认哈希函数 为 string 特化出一个版本
template <>
struct DefaultHashFunc<string>
{
	size_t operator()(const string& str)
	{
		// BKDR
		size_t hash = 0;
		for (auto ch : str) {
			hash *= 131;
			hash += ch;
		}
		return hash;
	}
};

// 哈希表模板参数控制
template<class K, class V, class HashFunc = DefaultHashFunc<K>>
class class HashTable
{}
  • 默认哈希函数 DefaultHashFunc 为模板设计，默认处理整型 ，直接返回 size_t 类型的整型值，方便外部进行取模运算
  • 对默认哈希函数模板进行特化 ，为string类型特化出一个版本，专用于处理 string 不能取模的问题，内部使用 BKDR 算法
    • 当哈希表的K为可取模的类型时 ：调用默认哈希函数，直接返回整型，可进行取模操作
    • 当哈希表的K为 字符串 类型时 ：调用特化版本的哈希函数 ，对字符串用 BKDR 算法计算出一个哈希冲突概率极低的、可取模的值
  • 关于模板的特化见前文链接 ：模版深入进阶及其特化

3. 哈希表的相关操作

insert

insert 函数的逻辑主要为三步：

  • 查找Key，如果Key已存在，就不进行插入
  • 插入前检查哈希表是否需要扩容
  • 检查容量后，进行线性探测，查找下一个可用于插入的位置进行插入
cpp 复制代码 
bool insert(const pair<K, V>& kv)
{
	if (find(kv.first))
		return false;

	// 插入前需要控制 负载因子 和 扩容
	//if ((static_cast<double> (_n) / static_cast<double>(_table.size())) >= 0.7)
	if (_n * 10 / _table.size() >= 7)		// 牺牲一部分空间换取性能
	{
		size_t newSize = _table.size() * 2;
		// 扩容后映射关系变了，需要重新映射
		// 创建一个新的 哈希表 处理映射关系 和 冲突
		HashTable<K, V, HashFunc> newHashTable;
		newHashTable._table.resize(newSize);
		// 遍历旧表的数据 重新插入，映射到新表   只把 存在的区域 进行映射
		for (size_t i = 0; i < _table.size(); i++)
		{
			if (_table[i]._state == EXIST)
			{
				// 这里再调用 insert 时，已经resize过了，会走下面的线性探测逻辑
				newHashTable.insert(_table[i]._kv);
			}
		}
		_table.swap(newHashTable._table);
	}

	// 线性探测
	HashFunc hs;
	size_t hashi = hs(kv.first) % _table.size();
	// 找到的 hashi 位置，可能 exist delete empty ，
	// 插入时 需要找到 线性探测，只要位置已有数据存在，就向后继续探测
	while (_table[hashi]._state == EXIST)
	{
		++hashi;
		hashi %= _table.size();
	}
	// 循环结束后，找到了  状态为 empty 和 delete 的位置都可以插入
	_table[hashi]._kv = kv;
	_table[hashi]._state = EXIST;
	++_n;
	return true;
}

查找：

  • if (find(kv.first))：如果当前Key已存在，不进行插入，返回false

线性探测：

  • 首先利用哈希函数提取关键字 Key 后，对 Key 做取模运算 ，计算hashi的值

  • 再在表中找下一个可用于插入的位置：

    • 状态为EMPTY和DELETE的位置都可以插入，因此只要当前位置状态为EXIST，就循环向后找(++hashi)。

    cpp 复制代码 
      while (_table[hashi]._state == EXIST)
  {
      ++hashi;
      hashi %= _table.size();
  }
    • 每次++hashi后，对hashi进行取模，使得 hasi 移动到_table.size()位置时，通过取模运算重新回到表的开头位置 ，找到EMPTY位置即可进行插入

  • 插入：

    • 插入pair ：_table[hashi]._kv = kv;
    • 插入后更新状态为EXIST ：_table[hashi]._state = EXIST;
    • 插入后有效元素计数++ ：++_n;

扩容逻辑 ：通过负载因子的大小判断哈希表是否需要扩容

  • 采取二倍扩容逻辑 ：size_t newSize = _table.size() * 2;

  • 由于扩容后旧表中原有的映射会失效，因此需要对旧表中的数据进行重新映射 ：这里采取的策略是==新创建一个局部哈希表，将旧表中的数据重新映射到新表==

    • 设置新表的大小 ：newHashTable._table.resize(newSize);

    • 遍历旧表，仅需将EXIST状态的结点映射到新表：

      cpp 复制代码 
        for (size_t i = 0; i < _table.size(); i++)
  {
      if (_table[i]._state == EXIST)
          newHashTable.insert(_table[i]._kv);
  }
      • for循环中新表再调用 insert时 ，新表已经 resize 过了，新表的大小为旧表的二倍，无需进行扩容，执行下面的线性探测逻辑 ，因此可以实现==将旧表中的数据重新映射到新表==

    • 映射完成后交换两个哈希表 中的vector，由于新表为局部哈希表，交换后，新表销毁时会自动销毁旧表的数据

find

cpp 复制代码 
HashData<const K, V>* find(const K& key) const
{
	// 线性探测
	HashFunc hs;

	size_t hashi = hs(key) % _table.size();
    // 仅在 不为 empty 的结点中查找
	while (_table[hashi]._state != EMPTY)
	{
		if (_table[hashi]._state == EXIST && _table[hashi]._kv.first == key)
		{
			return (HashData<const K, V>*) & _table[hashi];
		}
		++hashi;
		hashi %= _table.size();
	}
    // 循环内没有返回，说明没找到
	return nullptr;
}

查找逻辑：

  • 创建哈希函数对象 ，计算 Key 的hashi值

  • 查找时仅需在不为 empty 的结点中查找：while (_table[hashi]._state != EMPTY)

    • 状态为 EXIST 且 Key 值 == key 的结点即为要查找的位置

      cpp 复制代码 
        if (_table[hashi]._state == EXIST && _table[hashi]._kv.first == key)
  {
      return (HashData<const K, V>*) & _table[hashi];
  }

    • 每次循环内不满足查找条件时，++hashi 的值 去下一个位置查找

    • 每次 ++hashi 后，对 hashi 进行取模，使得 hasi 移动到_table.size()位置时，通过取模运算重新回到表的开头位置，便于进行第二轮查找

  • 找到时返回当前节点的地址，找不到时返回空指针

erase

  • 哈希表的删除需要找到对应的Key才能删除，因此需要先查找
cpp 复制代码 
bool Erase(const K& key)
{
	// 找到了才能删除
	HashData<const K, V>* ret = find(key);
	if (ret)
	{
		ret->_state = DELETE;
		--_n;
		return true;
	}
    // 找不到时 return false
	return false;
}

  • 查找 ：指针ret存储find的查找结果

  • 删除 ：if(ret)为真时，代表找到了，可进行删除。删除时无需抹除数据，只需要将该节点的状态设为DELETE即可，修改完状态后--_n，return true;

  • 找不到时直接return false;

八、链地址法/哈希桶 代码实现

1. 哈希结构

Hash 结点类型

cpp 复制代码 
template<class K, class V>
struct HashNode
{
	std::pair<K, V> _kv;
	struct HashNode<K, V>* _next;

	HashNode(const pair<K, V>& kv)
		:_kv(kv)
		,_next(nullptr)
	{ }
};

采用哈希桶设计，Hash数据类型为一个个的结点，使用单链表串起来：

  • std::pair<K, V> _kv；：存储键值对
  • struct HashNode<K, V>* _next;：单链表设计，存储指向下一个结点的指针
  • HashNode(const pair<K, V>& kv)：构造函数，初始化结点中的成员

哈希表结构设计

cpp 复制代码 
// 哈希表的结构
template<class K, class V, class HashFunc = DefaultHashFunc<K>>		// 默认使用整型的哈希函数
class HashTable
{
private:
	typedef struct HashNode<K, V> Node;		// 类型重命名

	vector<Node*> _table;	// 需要写析构函数
	size_t _n = 0;
public:
     // ... 相关成员函数实现
};
  • 哈希表定义为模板实现 ：模板参数设置为template<class K, class V, class HashFunc = DefaultHashFunc<K>>，设置pair中存储的数据K、V类型，并设置默认的哈希函数，同时支持传入自定义的哈希函数
  • 使用 vector 作为我们的表结构：由于 vector 为自定义类型，HashTable 的默认构造函数会自动调用 vector 的 默认构造函数
  • size_t _n = 0：存储有效数据的个数 ，哈希是分散存储的，vector 是连续存储的 ，_n 成员记录表中的有效结点个数，通过比较 _n 和 vector.size() 的大小判断哈希表是否需要扩容
  • 构造函数初始化哈希表 size 为10

2. 哈希函数设计

  • 链地址法同样需要仿函数来控制指字符串的取模问题

各自使用单独的仿函数设计

cpp 复制代码 
// 使用仿函数控制 string 和 其他整型的取模
template<class K>
struct DefaultHashFunc
{
	size_t operator()(const K& key)
	{
		return static_cast<size_t> (key);
	}
};


struct StringHashFunc
{
    size_t operator()(const string& str)
    {
        // BKDR
        size_t hash = 0;
        for (auto ch : str) {
            hash *= 131;
            hash += ch;
        }
        return hash;
    }
};

// 哈希表模板参数控制
template<class K, class V, class HashFunc = DefaultHashFunc<K>>
class class HashTable
{}

使用单独的仿函数设计 ：设计两个单独的仿函数，重载了operator()，通过哈希表的模板参数来空指取模运算

  • 默认哈希函数 ：DefaultHashFunc，默认关键字key为整型，直接返回整型，可以进行取模操作
  • 字符串的哈希函数 ： StringHashFunc：同样是返回一个整数，对字符串进行 BKDR 算法后，尽可能确保不同字符串的哈希值不同
  • 使用该方法设计出的哈希表，再使用时需要传入string的哈希函数HashTable<string, string, StringHashFunc> dict;但 STL 的使用并不需要传入哈希函数 ，接下来介绍使用模板及其特化解决该问题

使用模板及模板特化设计

  • STL 设计的使用并不需要传入哈希函数 ，下面介绍使用模板及其特化解决该问题
cpp 复制代码 
// 使用仿函数控制 string 和 其他整型的取模
template<class K>
struct DefaultHashFunc
{
	size_t operator()(const K& key)
	{
		return static_cast<size_t> (key);
	}
};

template <>
struct DefaultHashFunc<string>
{
	size_t operator()(const string& str)
	{
		// BKDR
		size_t hash = 0;
		for (auto ch : str) {
			hash *= 131;
			hash += ch;
		}
		return hash;
	}
};
// 哈希表模板参数控制
template<class K, class V, class HashFunc = DefaultHashFunc<K>>
class class HashTable
{}
  • 默认哈希函数 DefaultHashFunc 为模板设计，默认处理整型 ，直接返回 size_t 类型的整型值，方便外部进行取模运算
  • 对该哈希函数进行特出，为string类型特化出一个版本，专用于处理 string 不能取模的问题，内部使用 BKDR 算法
    • 当哈希表的K为可取模的类型时 ：调用默认哈希函数，直接返回整型，可进行取模操作
    • 当哈希表的K为 字符串 类型时 ：调用特化版本的哈希函数 ，对字符串用 BKDR 算法计算出一个可取模的值
  • 关于模板的特化见前文链接 ：模版深入进阶及其特化

3. 构造与析构函数

构造函数和开放定址法相似，只不过多了一个步骤：

  • 初始化哈希表size 为10
  • 初始化结点指针为 nullptr
cpp 复制代码 
public:
	HashTable()
	{
		_table.resize(10, nullptr);
	}
	// 需要手动析构桶中的节点
	~HashTable()
	{
		for (size_t i = 0; i < _table.size(); i++)
		{
			Node* curNode = _table[i];
			while (curNode)
			{
				Node* curNext = curNode->_next;
				
				delete curNode;
				curNode = curNext;
			}
			_table[i] = nullptr;
		}
	}

析构函数：

cpp 复制代码 
// 哈希表的结构
template<class K, class V, class HashFunc = DefaultHashFunc<K>>		// 默认使用整型的哈希函数
class HashTable
{
private:
	typedef struct HashNode<K, V> Node;		// 类型重命名

	vector<Node*> _table;	// 需要写析构函数
	size_t _n = 0;
public:
     // ... 相关成员函数实现
};

  • 回顾哈希表的设计，哈希表中的类型为自定义类型 vector ，编译器会自动调用 vector 的析构函数释放资源，但哈希桶中挂载的一个个结点不会被释放，因此需要我们设计析构函数释放每个桶中的节点

  • 析构函数核心设计 ：遍历每个桶，再遍历每个桶中的所有结点，依次释放结点即可

    cpp 复制代码 
      for (size_t i = 0; i < _table.size(); i++)
  {
      Node* curNode = _table[i];
      while (curNode)
      {
          Node* curNext = curNode->_next;
  
          delete curNode;
          curNode = curNext;
      }
      _table[i] = nullptr;
  }

4. 相关操作

Insert

Insert 函数的逻辑主要为三步：

  • 查找Key，如果Key已存在，就不进行插入
  • 插入前检查哈希表是否需要扩容
  • 检查容量后，查找对应的 hashi ，采用头插法进行插入
cpp 复制代码 
bool Insert(const pair<K, V>& kv)
{
	if (Find(kv.first))
		return false;

	HashFunc hf;

	// 控制负载因子 为 1 时扩容
	//if (static_cast<double> (_n) / static_cast<double> (_table.size()) == 1.0)
	if (_n == _table.size())		// 扩容逻辑
	{
		size_t newSize = _table.size() * 2;
		vector<Node*> newTable;;
		newTable.resize(newSize, nullptr);

		// 遍历每个桶，将每个桶中的节点都拿过来
		for (size_t i = 0; i < _table.size(); ++i)
		{
			Node* curNode = _table[i];
			while (curNode)
			{
				Node* curNext = curNode->_next;

				// 把旧表中的每个结点重新映射后，再头插到新表中
				size_t hashi = hf(curNode->_kv.first) % newSize;	
				// 头插
				curNode->_next = newTable[hashi];
				newTable[hashi] = curNode;
                
				curNode = curNext;
			}
			_table[i] = nullptr;
		}
		_table.swap(newTable);
	}
	// 挂结点的逻辑
	size_t hashi = hf(kv.first) % _table.size();

	Node* newNode = new Node(kv);
	// 头插
	newNode->_next = _table[hashi];
	_table[hashi] = newNode;
	++_n;
	return true;
}

查找：

  • if (Find(kv.first))：如果当前Key已存在，返回false

头插逻辑：

  • 首先利用哈希函数提取关键字Key后，对Key做取模运算 ，计算hashi的值，确定在哪个桶进行头插

  • 再在表中进行头插：

    • 创建新结点 ：Node* newNode = new Node(kv);

    • 头插逻辑：

      cpp 复制代码 
        // newNode 先链接，再成为新的头结点
  newNode->_next = _table[hashi];
  _table[hashi] = newNode;

    • 插入后有效元素计数++ ：++_n;

扩容逻辑 ：通过负载因子的大小判断哈希表是否需要扩容

  • 控制负载因子为1时进行扩容 ： if (_n == _table.size())，负载因子控制不大于1 ，可以确保每个桶的平均元素个数为1，因此查找的平均时间复杂度 为 O ( 1 ) O(1) O(1)

  • 由于扩容后旧表中原有的映射会失效，因此需要对旧表中的数据进行重新映射 ：这里采取的策略是==新创建一个局部哈希表，将旧表中的每个结点重新映射到新表==

    • 二倍扩容并设置新表的大小：

      cpp 复制代码 
        size_t newSize = _table.size() * 2;
  vector<Node*> newTable;;
  newTable.resize(newSize, nullptr);

    • 遍历每个桶中的的每个结点，计算相应的 hashi 值，再重新头插到新表中对应的桶中：

      cpp 复制代码 
        for (size_t i = 0; i < _table.size(); ++i)
  {
      Node* curNode = _table[i];
      while (curNode)
      {
          Node* curNext = curNode->_next;
  
          // 把每个结点做重新映射
          size_t hashi = hf(curNode->_kv.first) % newSize;	
          // 头插
          curNode->_next = newTable[hashi];
          newTable[hashi] = curNode;
  
          curNode = curNext;
      }
      _table[i] = nullptr;
  }
      • 每个桶插入过后，将旧桶中的指针置空

    • 映射完成后交换两个哈希表 中的vector，由于新表为局部哈希表，交换后，局部新表销毁时会自动销毁旧表的数据

Find

cpp 复制代码 
Node* Find(const K& key) const
{
	HashFunc hf;
	size_t hashi = hf(key) % _table.size();

	Node* curNode = _table[hashi];
	while (curNode)
	{
		if (curNode->_kv.first == key)
			return curNode;
		curNode = curNode->_next;
	}
	return nullptr;
}

查找逻辑 ：本质是单链表的查找

  • 创建哈希函数对象 ，计算 Key 的hashi值
  • 遍历 hashi 值对应的桶中的单链表：Node* curNode = _table[hashi];
    • 遍历单链表进行查找即可
  • 找到时返回当前节点的地址，找不到时返回空指针

Erase

  • 由于单链表的删除需要更改前一个结点的 next 指针 ，因此不适合复用 Find 函数
cpp 复制代码 
bool Erase(const K& key)
{
	HashFunc hf;
	size_t hashi = hf(key) % _table.size();

	Node* curPrev = nullptr;
	Node* curNode = _table[hashi];
	while (curNode)
	{
		if (curNode->_kv.first == key)
		{
			if (curPrev == nullptr) // 头删
				_table[hashi] = curNode->_next;	
			else  // 非头删
				curPrev->_next = curNode->_next;

			delete curNode;
			return true;
		}
		curPrev = curNode;
		curNode = curNode->_next;
	}
	return false;
}

  • 本质是单链表的删除，利用 prevNode 和 curNode 遍历单链表，对查找到的结点进行删除

  • 删除节点时，需要区分头删和非头删两种情况

    cpp 复制代码 
      if (curNode->_kv.first == key)
  {
      if (curPrev == nullptr) // 头删
          _table[hashi] = curNode->_next;	
      else  // 非头删
          curPrev->_next = curNode->_next;
  
      delete curNode;
      return true;
  }

  • **找到时，删除成功 return true，找不到时 return false; **

Print

  • 该函数实现的功能为打印每个桶中单链表的值 ，可根据需要进行格式自定义
cpp 复制代码 
void Print()
{
	for (size_t i = 0; i < _table.size(); ++i)
	{
		printf("[%d]->", i);
		Node* curNode = _table[i];
		while (curNode)
		{
			cout << curNode->_kv.first << ":" << curNode->_kv.second << "->";
			curNode = curNode->_next;
		}
		printf("NULL\n");
	}
	cout << endl;
}

九、使用素数优化哈希表的大小

在设计哈希表时，一个常见但容易被忽视的细节是：桶（bucket）数组的长度选择 。

很多初学者在实现哈希表时，往往直接让数组容量按倍数扩展，如 size *= 2。

这种做法虽然简单，但可能在哈希分布上留下隐患------当哈希函数的结果模式与桶容量存在某种数学关系（如公因数），则容易导致哈希冲突集中、性能急剧下降。

为了避免这种问题，工业级哈希表（如 std::unordered_map）通常会让桶数组的长度为素数（prime number） 。

这是因为素数在取模运算中能更均匀地分散哈希值，减少周期性冲突，从而提高查找与插入的效率。

获取下一个素数

下面的实现中，HashTable 构造函数初始容量为 11（素数）：

cpp 复制代码 
HashTable()
{
	_table.resize(11, nullptr);
}

而在扩容时，会调用 GetNextPrime() 获取下一个合适的素数容量：

cpp 复制代码 
inline size_t GetNextPrime(size_t prime)
{
	const int PRIMECOUNT = 28;
	static const size_t primeList[PRIMECOUNT] =
	{
		53ul, 97ul, 193ul, 389ul, 
		769ul, 1543ul, 3079ul, 6151ul, 
		12289ul, 24593ul, 49157ul, 98317ul, 
		196613ul, 393241ul, 786433ul, 1572869ul, 
		3145739ul, 6291469ul, 12582917ul, 25165843ul, 
		50331653ul, 100663319ul, 201326611ul, 402653189ul,
		805306457ul, 1610612741ul, 3221225473ul, 4294967291ul
	};

	size_t i = 0;
	for (; i < PRIMECOUNT; ++i)
	{
		if (primeList[i] > prime)
			return primeList[i];
	}
	return primeList[i];
}

这里预置了 28 个经过验证的素数，涵盖从几十到数十亿的范围。 当表满时，哈希表调用 GetNextPrime() 获取一个比当前容量更大的素数，作为新表的桶数。

扩容与重新映射过程

在 Insert() 函数中，当元素数量 _n 达到表的大小时，就会进行扩容：

cpp 复制代码 
// 以下为 insert 的扩容逻辑
if (_n == _table.size())
{
    // size_t newSize = _table.size() * 2;	 // 取代旧的扩容大小
	size_t newSize = GetNextPrime(_table.size());	 // 取代旧的扩容大小，扩容的其他步骤相同
	vector<Node*> newTable;
	newTable.resize(newSize, nullptr);
	
	// 重新哈希映射
	for (size_t i = 0; i < _table.size(); ++i)
	{
		Node* curNode = _table[i];
		while (curNode)
		{
			Node* curNext = curNode->_next;
			size_t hashi = hf(curNode->_kv.first) % newSize;
            // 头插
			curNode->_next = newTable[hashi];
			newTable[hashi] = curNode;
			curNode = curNext;
		}
		_table[i] = nullptr;
	}
	_table.swap(newTable);
}

整个过程包含三步：

  1. 选择新容量 ：通过 GetNextPrime() 找到更大的素数；
  2. 重新映射节点 ：将所有旧桶中的结点重新计算哈希值 并头插入新表；
  3. 交换表指针：用新表替换旧表，实现无缝扩容。

素数优化的意义

相比简单的"容量翻倍"方案，使用素数有以下优势：

  1. 降低哈希冲突概率：素数取模减少了哈希值周期性重复的可能；
  2. 提升查询与插入性能：分布更均匀，负载因子接近 1 时仍保持良好性能；
  3. 提升通用性：对于不同类型的哈希函数（尤其是简单的整数或字符串哈希），素数桶数能起到"天然扰动器"的作用，使映射更随机。

十、哈希表与红黑树性能对比

1. 测试代码

cpp 复制代码 
void test_speed()
{
	const size_t N = 1000000;

	unordered_set<int> us;
	set<int> s;

	vector<int> v;
	v.reserve(N);
	srand(time(0));
	for (size_t i = 0; i < N; ++i)
	{
		//v.push_back(rand());
		v.push_back(rand() + i * i + 13*i);
		//v.push_back(i);
	}

	size_t begin1 = clock();
	for (auto e : v)
	{
		s.insert(e);
	}
	size_t end1 = clock();
	cout << "set insert 耗时: " << end1 - begin1 << endl;

	size_t begin2 = clock();
	for (auto e : v)
	{
		us.insert(e);
	}
	size_t end2 = clock();
	cout << "unordered_set insert 耗时: " << end2 - begin2 << endl;

	cout << endl;

	size_t begin3 = clock();
	for (auto e : v)
	{
		s.find(e);
	}
	size_t end3 = clock();
	cout << "set find 耗时: " << end3 - begin3 << endl;

	size_t begin4 = clock();
	for (auto e : v)
	{
		us.find(e);
	}
	size_t end4 = clock();
	cout << "unordered_set find 耗时: " << end4 - begin4 << endl << endl;

	cout << "插入数据个数：" << s.size() << endl;
	cout << "插入数据个数：" << us.size() << endl << endl;;

	size_t begin5 = clock();
	for (auto e : v)
	{
		s.erase(e);
	}
	size_t end5 = clock();
	cout << "set erase 耗时: " << end5 - begin5 << endl;

	size_t begin6 = clock();
	for (auto e : v)
	{
		us.erase(e);
	}
	size_t end6 = clock();
	cout << "unordered_set erase 耗时: " << end6 - begin6 << endl << endl;
}
int main()
{
    test_speed();
    return 0;
}

2. 结果分析

  • 插入随机数据：
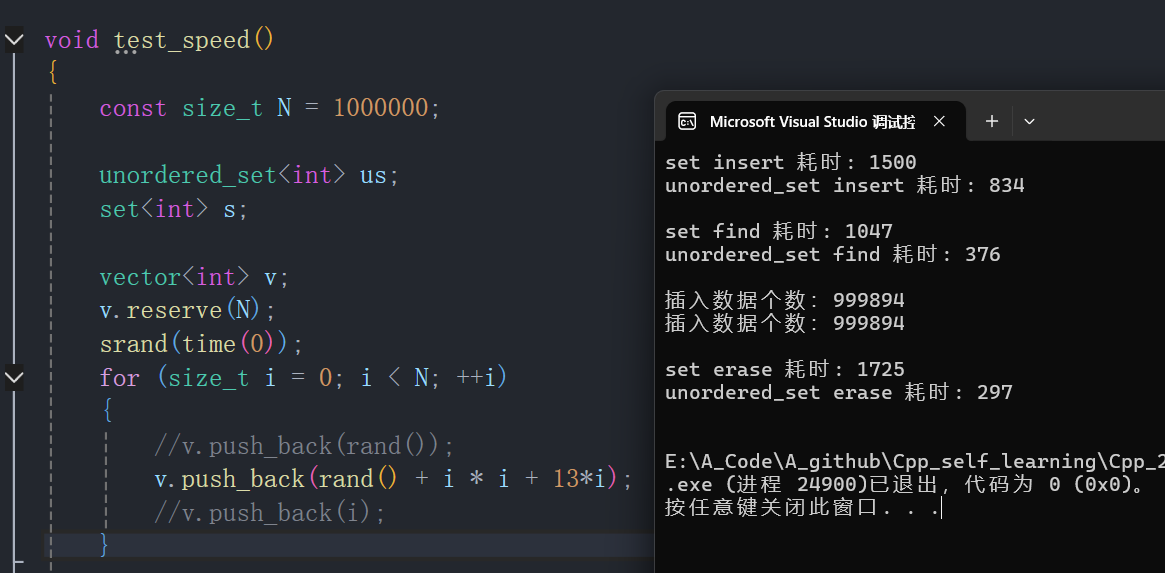
  • 插入有序数据：

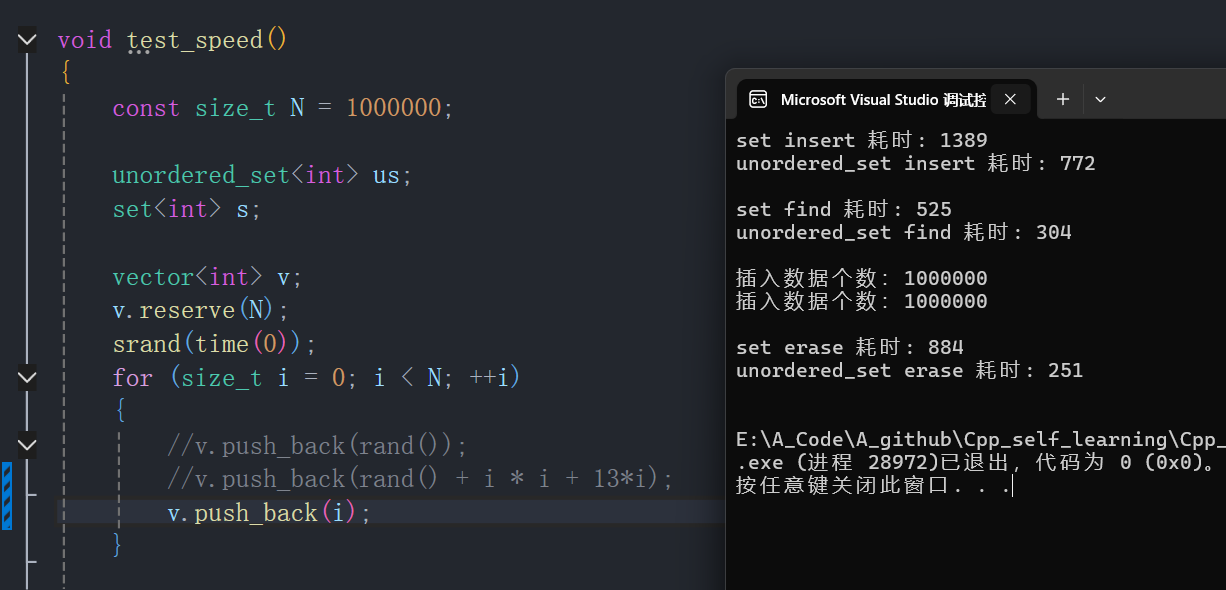
一、实验结果说明

虽然不同机器、编译器、随机数分布可能导致绝对时间不同，但趋势是非常稳定的：

操作类型 set（红黑树） unordered_set（哈希表） 原因分析
插入 慢 快 哈希表平均 O(1)，红黑树 O(logN)
查找 慢 快 哈希表直接定位桶，红黑树需要多次比较
删除 慢 快 红黑树删除要维持平衡，哈希表平均 O(1)
有序性 有序 无序 红黑树保持中序有序，哈希表完全无序
实验结果的核心结论：

哈希表型容器（unordered_set / unordered_map）在插入、查找、删除操作上远快于红黑树型容器（set / map）。

但红黑树型容器具备自动排序、有序遍历和范围查询能力，是哈希表无法替代的。

二、两类容器底层机制区别

对比项 set/map（红黑树） unordered_set/unordered_map（哈希表）
底层结构 红黑树（平衡二叉搜索树） 哈希表（数组 + 链表/桶）
元素有序性 自动排序（中序遍历有序） 无序存储
插入复杂度 O(logN) 平均 O(1)
查找复杂度 O(logN) 平均 O(1)
删除复杂度 O(logN) 平均 O(1)
空间开销 相对较小 需要额外哈希桶，空间大
内部机制 通过比较函数维护平衡 通过哈希函数定位桶
迭代器稳定性 插入删除后仍有效 rehash 时所有迭代器失效
支持范围操作 ✔（lower_bound, upper_bound） ❌（无序无法范围查找）

三、适用场景总结

使用场景 推荐容器 原因
需要保持元素有序 set / map 红黑树自动排序，可用中序遍历输出有序结果
需要范围查找（如区间查询、上下界） set / map 支持 lower_bound() / upper_bound()
频繁插入、查找、删除（只关心是否存在） unordered_set / unordered_map 哈希结构，平均 O(1) 时间复杂度，速度远快
键值分布随机、冲突较少 unordered_set / unordered_map 哈希表性能极佳
键值分布集中或需要自定义比较顺序 set / map 哈希冲突可能严重时，树结构更稳定
内存敏感或要求迭代器稳定 set / map 哈希表扩容（rehash）会使迭代器失效

四、总结

✅ 红黑树（set/map） ：适合有序数据、范围查找、稳定性要求高的场景。

✅ 哈希表（unordered_set/unordered_map）：适合频繁查找、插入、删除且不要求顺序的高性能场景。

十一、完整代码实现

1. 开放定址法

cpp 复制代码 
// 闭散列的 开放定址法的哈希表
namespace open_addr
{
	// 哈希表中每个位置的状态
	enum STATE
	{
		EXIST,
		EMPTY,
		DELETE
	};

	// 哈希存储的数据
	template<class K, class V>
	struct HashData
	{
		std::pair<K, V> _kv;
		enum STATE _state = EMPTY;
	};

	// 使用仿函数控制 string 和 其他整型的取模
	template<class K>
	struct DefaultHashFunc
	{
		size_t operator()(const K& key)
		{
			return static_cast<size_t> (key);
		}
	};

	//// 方式一: 专门为 string 写一个 哈希函数，使用第一个 char 控制
	//struct StringHashFunc
	//{
	//	size_t operator()(const string& str)
	//	{
	//		return static_cast<size_t> (str[0]);
	//	}
	//};

	// 为 string 特化一个版本 哈希函数

	template <>
	struct DefaultHashFunc<string>
	{
		size_t operator()(const string& str)
		{
			// BKDR 哈希算法
			size_t hash = 0;
			for (auto ch : str) {
				hash *= 131;
				hash += ch;
			}
			return hash;
		}
	};

	// 哈希表的结构
	template<class K, class V, class HashFunc = DefaultHashFunc<K>>		// 默认使用整型的哈希函数
	class HashTable
	{
	private:
		vector<HashData<K, V>> _table;	// vector 存自定义类型，无需实现析构函数
		size_t _n = 0;  // 存储的有效数据的个数   哈希是分散存储的，vector 是连续存储的，因此即使 vector 中有 size,也需要这个 _n

	public:
		HashTable()
		{
			_table.resize(10);
		}
		bool insert(const pair<K, V>& kv)
		{
			if (find(kv.first))
				return false;

			// 插入前需要控制 负载因子 和 扩容
			//if ((static_cast<double> (_n) / static_cast<double>(_table.size())) >= 0.75)
			if (_n * 10 / _table.size() >= 7)		// 牺牲一部分空间换取性能
			{
				size_t newSize = _table.size() * 2;
				// 扩容后映射关系变了，需要重新映射
				// 创建一个新的 哈希表 处理映射关系 和 冲突
				HashTable<K, V, HashFunc> newHashTable;
				newHashTable._table.resize(newSize);
				// 遍历旧表的数据 重新插入，映射到新表   只把 存在的区域 进行映射
				for (size_t i = 0; i < _table.size(); i++)
				{
					if (_table[i]._state == EXIST)
					{
						// 这里再调用 insert 时，已经resize过了，会走下面的线性探测逻辑
						newHashTable.insert(_table[i]._kv);
					}
				}
				_table.swap(newHashTable._table);
			}

			// 线性探测
			HashFunc hs;
			size_t hashi = hs(kv.first) % _table.size();
			// 找到的 hashi 位置，可能 exist delete empty ，
			// 插入时 需要找到 线性探测，只要位置已有数据存在，就向后继续探测
			while (_table[hashi]._state == EXIST)
			{
				++hashi;
				hashi %= _table.size();
			}
			// 循环结束后，找到了  状态为 empty 和 delete 的位置都可以插入
			_table[hashi]._kv = kv;
			_table[hashi]._state = EXIST;
			++_n;
			return true;
		}
		HashData<const K, V>* find(const K& key) const
		{
			// 线性探测
			HashFunc hs;

			size_t hashi = hs(key) % _table.size();
			while (_table[hashi]._state != EMPTY)
			{
				if (_table[hashi]._state == EXIST && _table[hashi]._kv.first == key)
				{
					//return (HashData<const K, V>*) & _table[hashi];
					return (HashData<const K, V>*) & _table[hashi];
				}
				++hashi;
				hashi %= _table.size();
			}
			return nullptr;
		}

		bool Erase(const K& key)
		{
			// 找到了才能删除
			HashData<const K, V>* ret = find(key);
			if (ret)
			{
				ret->_state = DELETE;
				--_n;
				return true;
			}
			return false;
		}
	};
}

2. 链地址法/哈希桶法（更重要）

cpp 复制代码 
namespace hash_bucket
{
	// 使用仿函数控制 string 和 其他整型的取模
	template<class K>
	struct DefaultHashFunc
	{
		size_t operator()(const K& key)
		{
			return static_cast<size_t> (key);
		}
	};

	//// 方式一: 专门为 string 写一个 哈希函数，使用第一个 char 控制
	//struct StringHashFunc
	//{
	//	size_t operator()(const string& str)
	//	{
	//		return static_cast<size_t> (str[0]);
	//	}
	//};

	// 为 string 特化一个版本 哈希函数

	template <>
	struct DefaultHashFunc<string>
	{
		size_t operator()(const string& str)
		{
			// BKDR
			size_t hash = 0;
			for (auto ch : str) {
				hash *= 131;
				hash += ch;
			}
			return hash;
		}
	};

	template<class K, class V>
	struct HashNode
	{
		std::pair<K, V> _kv;
		struct HashNode<K, V>* _next;

		HashNode(const pair<K, V>& kv)
			:_kv(kv)
			, _next(nullptr)
		{
		}
	};

	template<class K, class V, class HashFunc = DefaultHashFunc<K>>
	class HashTable
	{
		typedef struct HashNode<K, V> Node;
	private:
		vector<Node*> _table;	// 需要写析构函数，桶中的节点需要手动析构
		size_t _n = 0;

	public:
		HashTable()
		{
			_table.resize(10, nullptr);
		}
		// 需要手动析构桶中的节点
		~HashTable()
		{
			for (size_t i = 0; i < _table.size(); i++)
			{
				Node* curNode = _table[i];
				while (curNode)
				{
					Node* curNext = curNode->_next;

					delete curNode;
					curNode = curNext;
				}
				_table[i] = nullptr;
			}
		}


		bool Insert(const pair<K, V>& kv)
		{
			if (Find(kv.first))
				return false;

			HashFunc hf;
			// 扩容逻辑
			// 控制负载因子 为 1 时扩容
			//if (static_cast<double> (_n) / static_cast<double> (_table.size()) >= 1.0)

			// 控制负载因子 到 1 时扩容
			if (_n == _table.size())
			{
				size_t newSize = _table.size() * 2;
				vector<Node*> newTable;;
				newTable.resize(newSize, nullptr);

				// 遍历每个桶，将每个桶中的节点都拿过来
				for (size_t i = 0; i < _table.size(); ++i)
				{
					Node* curNode = _table[i];
					while (curNode)
					{
						Node* curNext = curNode->_next;

						// 把每个结点做重新映射
						size_t hashi = hf(curNode->_kv.first) % newSize;	
						// 头插
						curNode->_next = newTable[hashi];
						newTable[hashi] = curNode;

						//curNode = curNode->_next;
						curNode = curNext;
					}
					_table[i] = nullptr;
				}
				_table.swap(newTable);
			}
			// 挂结点的逻辑
			size_t hashi = hf(kv.first) % _table.size();

			Node* newNode = new Node(kv);
			// 头插
			newNode->_next = _table[hashi];
			_table[hashi] = newNode;
			++_n;
			return true;
		}

		Node* Find(const K& key) const
		{
			HashFunc hf;
			size_t hashi = hf(key) % _table.size();

			Node* curNode = _table[hashi];
			while (curNode)
			{
				if (curNode->_kv.first == key)
					return curNode;
				curNode = curNode->_next;
			}
			return nullptr;
		}

		// 单链表的删除需要更改前一个结点的 next 指针，不适合复用 find
		bool Erase(const K& key)
		{
			HashFunc hf;
			size_t hashi = hf(key) % _table.size();

			Node* curPrev = nullptr;
			Node* curNode = _table[hashi];
			while (curNode)
			{
				if (curNode->_kv.first == key)
				{
					if (curPrev == nullptr) // 头删
						_table[hashi] = curNode->_next;
					else  // 非头删
						curPrev->_next = curNode->_next;

					delete curNode;
					--_n;
					return true;
				}
				curPrev = curNode;
				curNode = curNode->_next;
			}
			return false;
		}
		void Print()
		{
			for (size_t i = 0; i < _table.size(); ++i)
			{
				printf("[%d]->", (int)i);
				Node* curNode = _table[i];
				while (curNode)
				{
					cout << curNode->_kv.first << ":" << curNode->_kv.second << "->";
					curNode = curNode->_next;
				}
				printf("NULL\n");
			}
			cout << endl;
		}
	};
}

结语

哈希表 以简单的思想实现了极高的效率，但其背后蕴含着精妙的算法与设计权衡。

本文从理论到实践展示了哈希函数、冲突处理、扩容机制及与红黑树的性能差异。

实际开发中：

  • 追求速度 → 选用 哈希表（unordered 系列）
  • 需要有序与范围查询 → 选用 红黑树（set/map）

理解哈希表的底层原理，不仅能优化代码性能，更能加深对数据结构与系统设计的整体把握。

以上就是本文的所有内容了，如果觉得文章对你有帮助，欢迎 点赞⭐收藏 支持！如有疑问或建议，请在评论区留言交流，我们一起进步

分享到此结束啦
一键三连，好运连连！

你的每一次互动，都是对作者最大的鼓励！

征程尚未结束，让我们在广阔的世界里继续前行！ 🚀

相关推荐
Larry_Yanan4 小时前
QML学习笔记（五十一）QML与C++交互：数据转换——基本数据类型
c++·笔记·学习
梵尔纳多4 小时前
ffmpeg 使用滤镜实现播放倍速
c++·qt·ffmpeg
路由侠内网穿透.4 小时前
本地部署网站流量分析工具 Matomo 并实现外部访问
运维·服务器·远程工作
nju_spy5 小时前
力扣每日一题（四）线段树 + 树状数组 + 差分
数据结构·python·算法·leetcode·面试·线段树·笔试
dnpao5 小时前
在服务器已有目录中部署 Git 仓库
运维·服务器·git
白曦5 小时前
switch语句的使用
c++
冰糖拌面5 小时前
GO写的http服务，清空cookie
服务器·http·golang
超越自己5 小时前
远程连接银河麒麟服务器-xrdp方式
linux·运维·服务器·远程桌面·银河麒麟
Candice_jy5 小时前
vscode运行ipynb文件：使用docker中的虚拟环境
服务器·ide·vscode·python·docker·容器·编辑器
热门推荐
01GitHub 镜像站点02综合整理：pdf预览显示：你尝试预览的文件可能对你的计算机有害。如果你信任此文件以及其来源，请打开此文件以看其内容，如何解决以正常预览文件03UV安装并设置国内源04npm使用国内淘宝镜像的方法05Linux下V2Ray安装配置指南06安娜的档案(Anna’s Archive) 镜像网站/国内最新可访问入口（持续更新）07BongoCat - 跨平台键盘猫动画工具08《大数据技术原理与应用》实验报告三 熟悉HBase常用操作09NVIDIA显卡驱动、CUDA、cuDNN 和 TensorRT 版本匹配指南10GitLab 零基础入门指南：从安装到项目管理全流程