目录
[八*、集合(排序+双指针 / set去重)](#八*、集合(排序+双指针 / set去重))
一*、小易的升级之路(数学)


就是求最大公约数,直接用gcd函数,不过得记得头文件 #include<numeric>
如果是暴力的话会超时,或者手搓一个gcd函数,这里推荐使用欧几里得算法,时间复杂度最低。

可以进一步优化,说实话还是感觉上面的代码更好理解。
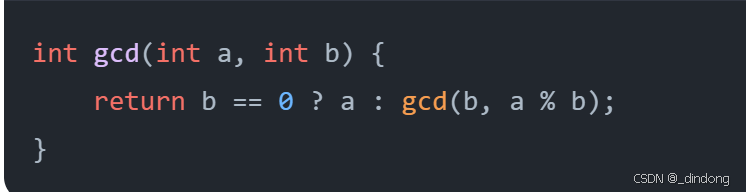
记得这种算法可以用装修用固定大小的瓷砖填地板解释,或者该用切蛋糕来解释吧,比如我有一块24x16(cm)的蛋糕,要求切成大小相同的正方形蛋糕,但不能剩余,问切出的蛋糕最大边长是多少?答案就是24和16的最大公约数。而欧几里得算法得到这个最大公约数的求解过程,就可以理解为:
第一次用较小的边尝试,切出一块16x16的蛋糕,但是有剩余,不符合题意,那么我们就要去更小的那部分里边找边长更小的正方形(这里边找出的结果,最终在更大的那部分比如这里是16x16,一定能切出很多结果边长大小的正方形,并且一定不会有剩余),然后继续在小的里边继续切,思路依然是用小的那条边当作大小来切。然后找到8,8可以,且较大边%8==0,a=temp(8),b=a%b也就是等于0,然后下一次循环,b==0退出循环,a==8就是最终结果。也就是说,我们每次都选择较小边当作切成的蛋糕大小,如果没有剩余,那么此时就是最大公约数。如果有剩余,那么我们以剩下那部分的两条边长作为参数,不断进行这种操作,直到出现结果。妙啊。
代码实现如下:
cpp
#include <iostream>
#include <numeric>
using namespace std;
using LL=long long;
int main() {
LL n,x;
cin>>n>>x;
LL Mlevel;
for(int i=0;i<n;++i)
{
cin>>Mlevel;
if(x>=Mlevel)x+=Mlevel;
else
{
x+=gcd(x, Mlevel);
}
}
cout<<x;
return 0;
}二、礼物的最大价值(路径dp)

相当基础的路径dp题,不知道是不是第一天所以这么简单?
cpp
#include <vector>
class Solution {
public:
int maxValue(vector<vector<int> >& grid) {
int m=grid.size(),n=grid[0].size();
vector<vector<int>> dp(m+1,vector<int>(n+1));
for(int i=1;i<=m;++i)
{
for(int j=1;j<=n;++j)
{
dp[i][j]=grid[i-1][j-1]+max(dp[i-1][j],dp[i][j-1]);
}
}
return dp[m][n];
}
};三*、对称之美(双指针/哈希)

解法一:双指针
开始还以为要dfs全排列,然后判断是不是回文,心想这太复杂了,然后写出dfs全排列+判断回文的代码,运行过了ok提交,果不其然超时了。然后想着想着不就是判断1对应n-1,2对应n-2以此类推判断是不是有重复元素嘛,这样现将字符串存进数组,然后用双指针就能搞定了,写一个判断回文的函数不就是判断有没有Same
代码实现如下:
cpp
#include <iostream>
#include <ostream>
using namespace std;
#include<vector>
#include<algorithm>
bool HasSameChar(string s1,string s2)
{
sort(s1.begin(),s1.end());
sort(s2.begin(),s2.end());
int cur1=0,cur2=0;
while(cur1<s1.size()&&cur2<s2.size())
{
if(s1[cur1]<s2[cur2])++cur1;
else if(s1[cur1]>s2[cur2])++cur2;
else return true;
}
return false;
}
int main() {
int t;
cin>>t;
int n;
while(t--)
{
cin>>n;
vector<string> s(n);
for(int i=0;i<n;++i)cin>>s[i];
//因为输出的二元性,所以我用bool变量来标识
bool flag=true;
int left=0,right=n-1;
while(left<right)
{
if(!HasSameChar(s[left], s[right]))
{
flag=false;
break;
}
++left;
--right;
}
if(flag)cout<<"Yes"<<endl;
else cout<<"No"<<endl;
}
return 0;
}解法二:哈希
判重判重,第一个想到的不就是哈希嘛
我们用一个二维数组来模拟哈希表的思路,第一个位置表示第几个字符串,第二个位置用于表示哪个字母,所以我们开[101][26]这样的大小
cpp
#include<iostream>
#include<string>
#include<cstring>
using namespace std;
bool vis[110][26];//用来标记每一行 字母是否存在
int t,n;
string s;
bool check(int left,int right){
//26个字母暴力检查有没有
for(int i=0;i<26;++i)
if(vis[left][i]&&vis[right][i]) return true;
return false;
}
int main(){
cin>>t;
while(t--){
//先清空hash表
memset(vis,0,sizeof vis);
cin>>n;//知道了有多少个字符串
for(int i=0;i<n;++i){
cin>>s;
for(auto&ch:s) vis[i][ch-'a']=true;
}
//双指针向中间靠
int left=0,right=n-1;
for(;left<right;++left,--right)
if(!check(left,right)) break;
//left<right为假说明只是越界导致结束,输出Yes
cout<<(left<right?"No":"Yes")<<endl;
}
return 0;
}今天三道都写出来了,希望明天也能都写出来hhh\(^o^)/~
实则不然
四、经此一役小红所向无敌
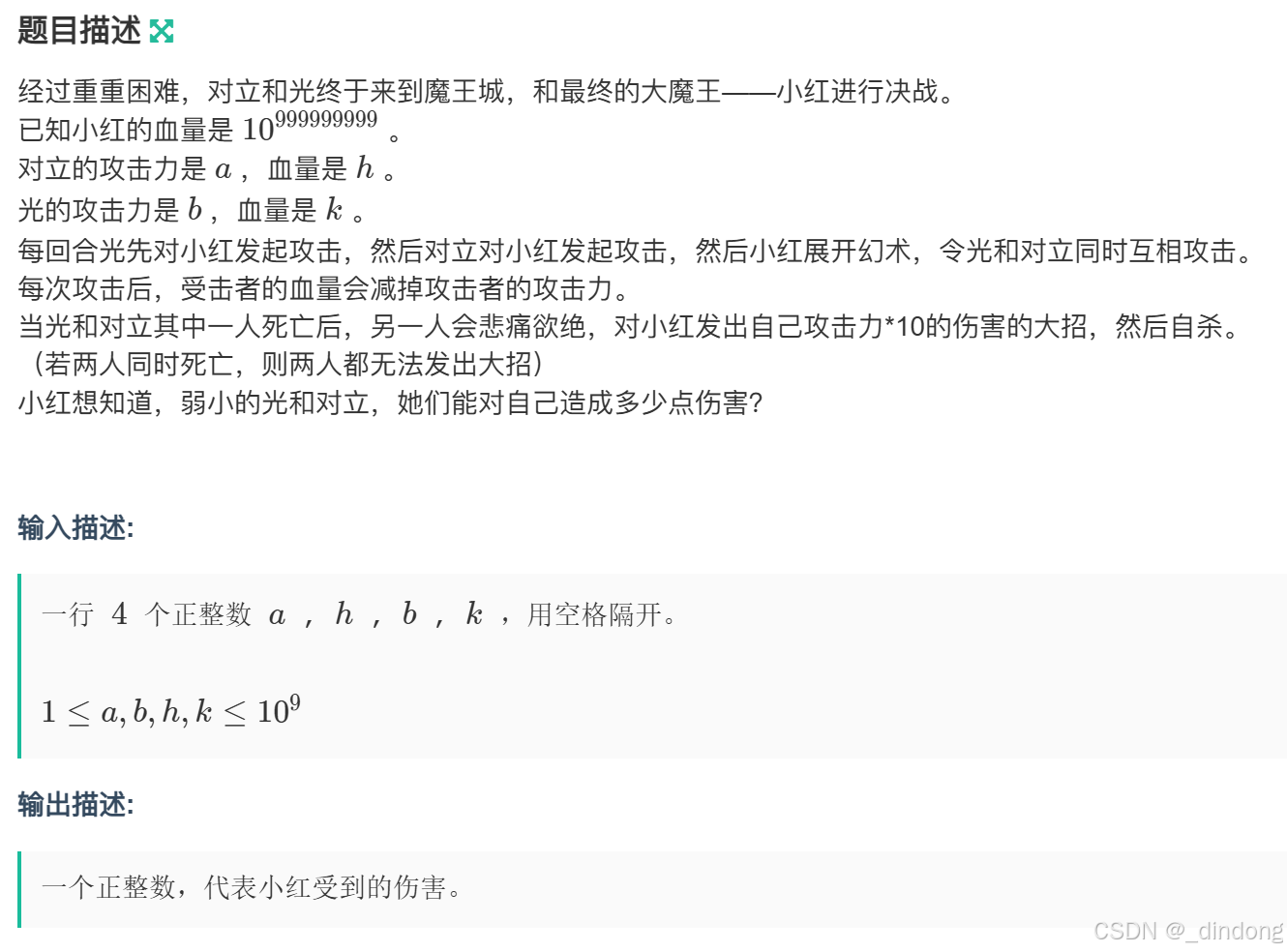
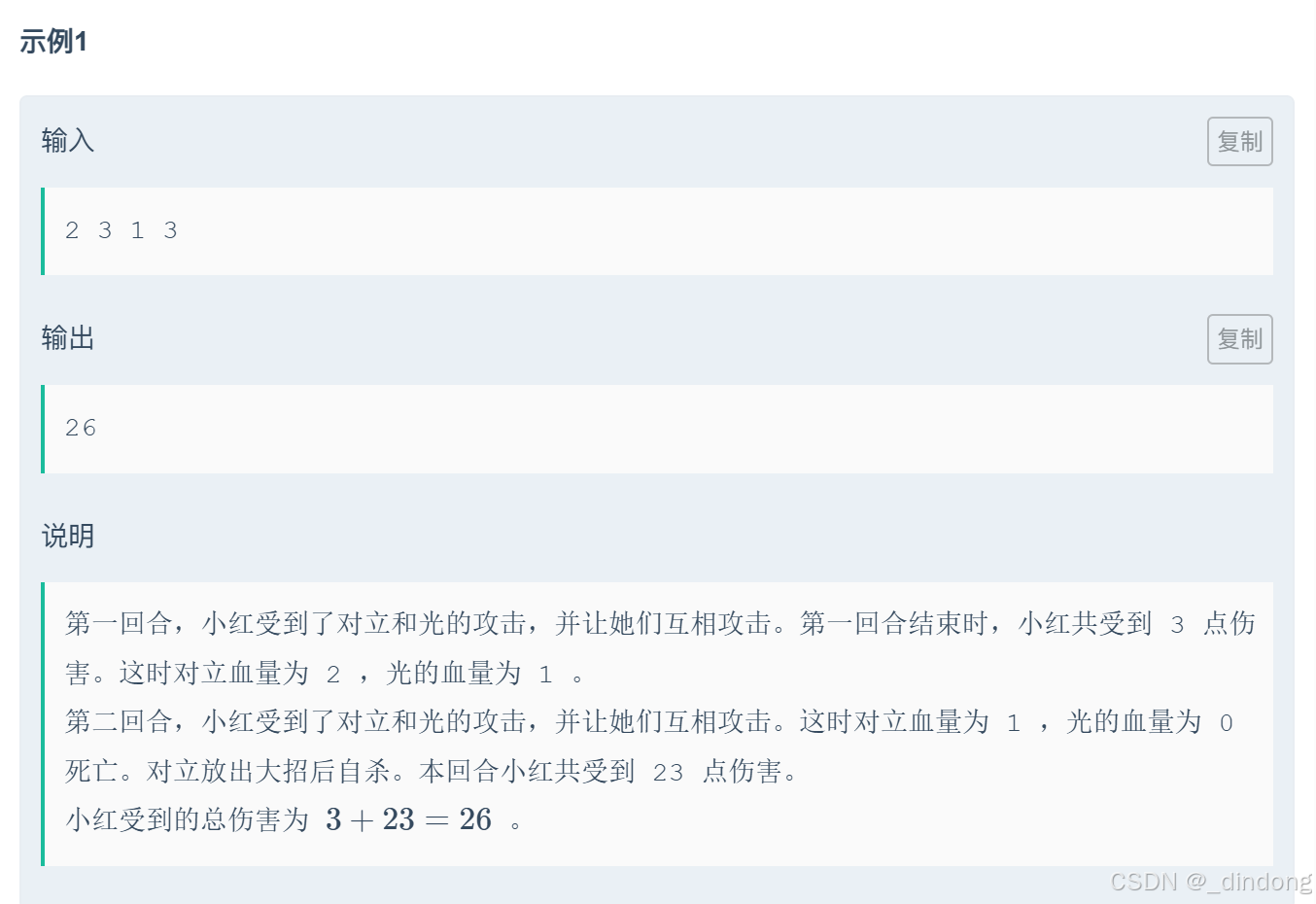
模拟:会超时
cpp
#include <iostream>
using namespace std;
using LL=long long;
int main() {
LL a,h,b,k;
cin>>a>>h>>b>>k;
LL sum=0;
while(h&&k)
{
sum+=(a+b);
h-=b;
k-=a;
if(h<=0&&k<=0)break;
if(h<=0&&k)
{
sum+=(b*10);
break;
}
if(k<=0&&h)
{
sum+=(a*10);
break;
}
}
cout<<sum;
return 0;
}优化一下就是,提前统计一下互砍的次数,取min
cpp
#include<iostream>
using namespace std;
typedef long long LL;
LL a,h,b,k;
int main(){
cin>>a>>h>>b>>k;
LL ret=0;//累计伤害
//看看两个人能互砍多少回合
LL n=min(h/b,k/a);
ret+=n*(a+b);
//计算剩余血量
h-=b*n;
k-=a*n;
//看看是不是都活着 如果都活着就再砍一下
if(h>0&&k>0){
h-=b;
k-=a;
ret+=a+b;
}
//这时候至少死了一个 或者两个都死了
if(h>0||k>0) ret+=10*(h>0?a:b);
cout<<ret<<endl;
return 0;
}五*、连续子数组最大和(线性dp)

没有做出来,看来近期要复习dp了。。。
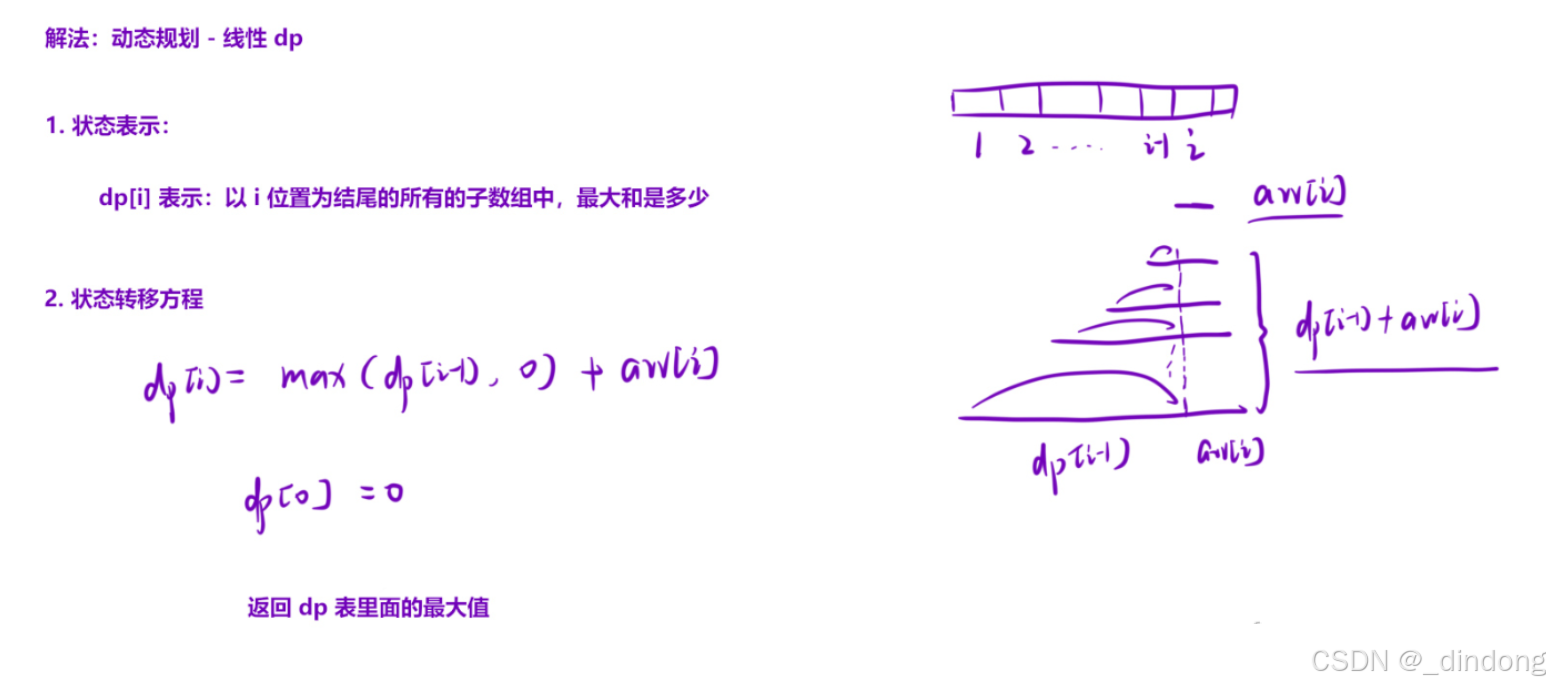
cpp
#include <iostream>
#include <algorithm>
using namespace std;
const int N=2e5+10;
int nums[N],dp[N];
int n;
int main() {
cin>>n;
int ret=-101;
for(int i=1;i<=n;++i) cin>>nums[i];
for(int i=1;i<=n;++i){
dp[i]=max(dp[i-1],0)+nums[i];
ret=max(dp[i],ret);
}
cout<<ret<<endl;
return 0;
}六*、非对称之美(贪心+找规律)
所谓题干越短,杀伤力越强?
情况1:所以字符都一样 return 0
情况2:整个串都是回文 return n-1
情况3:整个串不是回文 return n
佩服。。。。这就是非对称之美吗
cpp
#include<iostream>
#include<string>
using namespace std;
string s;
int func(){
int n=s.size();
//首先要判断是否全都相同
int i=1;
for(;i<n;++i)
if(s[i]!=s[0]) break;
if(i==n) return 0;
//接下来双指针往中间靠,判断整个字符串是否都是回文串
int left=0,right=n-1;
for(;left<right;++left,--right)
if(s[left]!=s[right]) break;
return left<right?n:n-1;
}
int main(){
cin>>s;
cout<<func()<<endl;
return 0;
}七*、爱丽丝的人偶(贪心)


没有思路
看完解答后发现只要让数组的数据是波形的就行
cpp
#include<iostream>
using namespace std;
int n;
int main(){
cin>>n;
//必须有单调性,所以就一高一矮 这样放
int left=1,right=n;
while(left<=right){
cout<<left++<<" ";
if(left<=right) cout<<right--<<" ";
}
return 0;
}八*、集合(排序+双指针 / set去重)

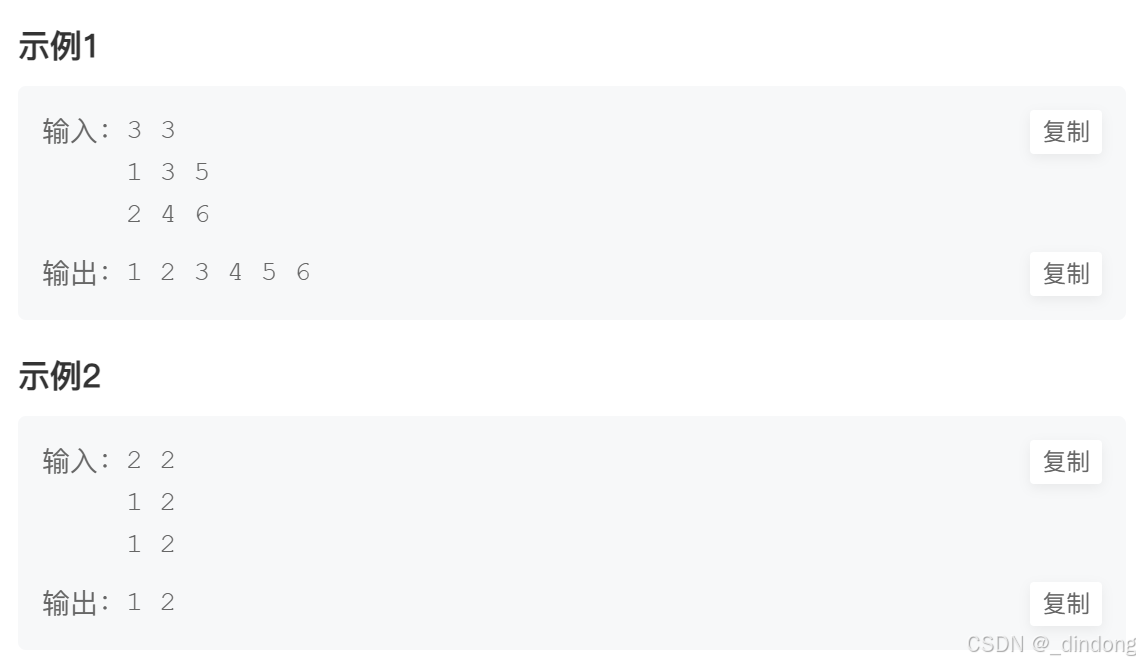
解法一:排序+双指针
因为使用双指针算法,不要忘记排序。此外,注意可能会有重复元素!
其实这也是一种归并思路
cpp
#include <iostream>
#include <algorithm>
using namespace std;
int n,m;
const int N=1e4+10;
int a[N],b[N];
int main() {
cin>>n>>m;
for(int i=0;i<n;++i) cin>>a[i];
for(int i=0;i<m;++i) cin>>b[i];
sort(a,a+n);
sort(b,b+m);
//双指针归并 小的插入后++
int cur1=0,cur2=0;
while(cur1<n&&cur2<m){
if(a[cur1]<b[cur2]){
cout<<a[cur1++]<<" ";
while(a[cur1]==a[cur1-1]) ++cur1;
}
else if(a[cur1]>b[cur2]){
cout<<b[cur2++]<<" ";
while(b[cur2]==a[cur2-1]) ++cur2;
}
else{
cout<<a[cur1++]<<" ";
++cur2;
while(a[cur1]==a[cur1-1]) ++cur1;
while(b[cur2]==a[cur2-1]) ++cur2;
}
}
//有一组还没走完
while(cur1<n){
if(cur1==0||a[cur1]!=a[cur1-1]) cout<<a[cur1]<<" ";
++cur1;
}
while(cur2<m){
if(cur2==0||b[cur2]!=b[cur2-1]) cout<<b[cur2]<<" ";
++cur2;
}
return 0;
}
// 64 位输出请用 printf("%lld")解法二:set(set容器默认对数据升序排序,而且会去重)
cpp
#include <iostream>
#include <set>
using namespace std;
int n,m;
set<int> s;
int main() {
cin>>n>>m;
int x;
while(n--){
cin>>x;
s.insert(x);
}
while(m--){
cin>>x;
s.insert(x);
}
for(auto&e:s) cout<<e<<" ";
return 0;
}
// 64 位输出请用 printf("%lld")九、最长回文子序列(区间dp)


没想到自己一遍做出来了,开心啊
cpp
#include <iostream>
#include <vector>
using namespace std;
int main() {
//dp[i][j]表示i~j区域内的最长回文子序列
string s;
cin>>s;
int n=s.size(),len=1;
vector<vector<int>> dp(n,vector<int>(n,1));
//因为第一个位置会使用后续的位置,所以倒着填
for(int i=n-1;i>=0;--i)
{
for(int j=i+1;j<n;++j)
{
if(s[i]==s[j])
{
dp[i][j]=i+1<j?dp[i+1][j-1]+2:2;
}
else dp[i][j]=max(dp[i+1][j],dp[i][j-1]);
len=max(len,dp[i][j]);
}
}
cout<<len;
return 0;
}十*、添加字符(枚举)

本来以为是匹配最长的连续的长度,然后字符串长度减去求得的最长长度来做,但是匹配可以在A串的任何一个位置匹配,如果第一个位置不同但后续相同,代码就出错了,比如xello和hello,最终输出5因为求得最长长度为0,但答案应该为1所以还是枚举吧
cpp
#include <iostream>
#include <string>
using namespace std;
string a,b;
int main() {
cin>>a>>b;
int m=a.size(),n=b.size();
//不相等的最多就是m个
int ret=m;
for(int i=0;i<=n-m;++i){//枚举b的起始位置
int tmp=0;//统计不同位数的个数
for(int j=0;j<m;++j)
if(a[j]!=b[i+j]) ++tmp;
ret=min(ret,tmp);
}
cout<<ret<<endl;
}
// 64 位输出请用 printf("%lld")十一*、数组变换(贪心+位运算+数学)
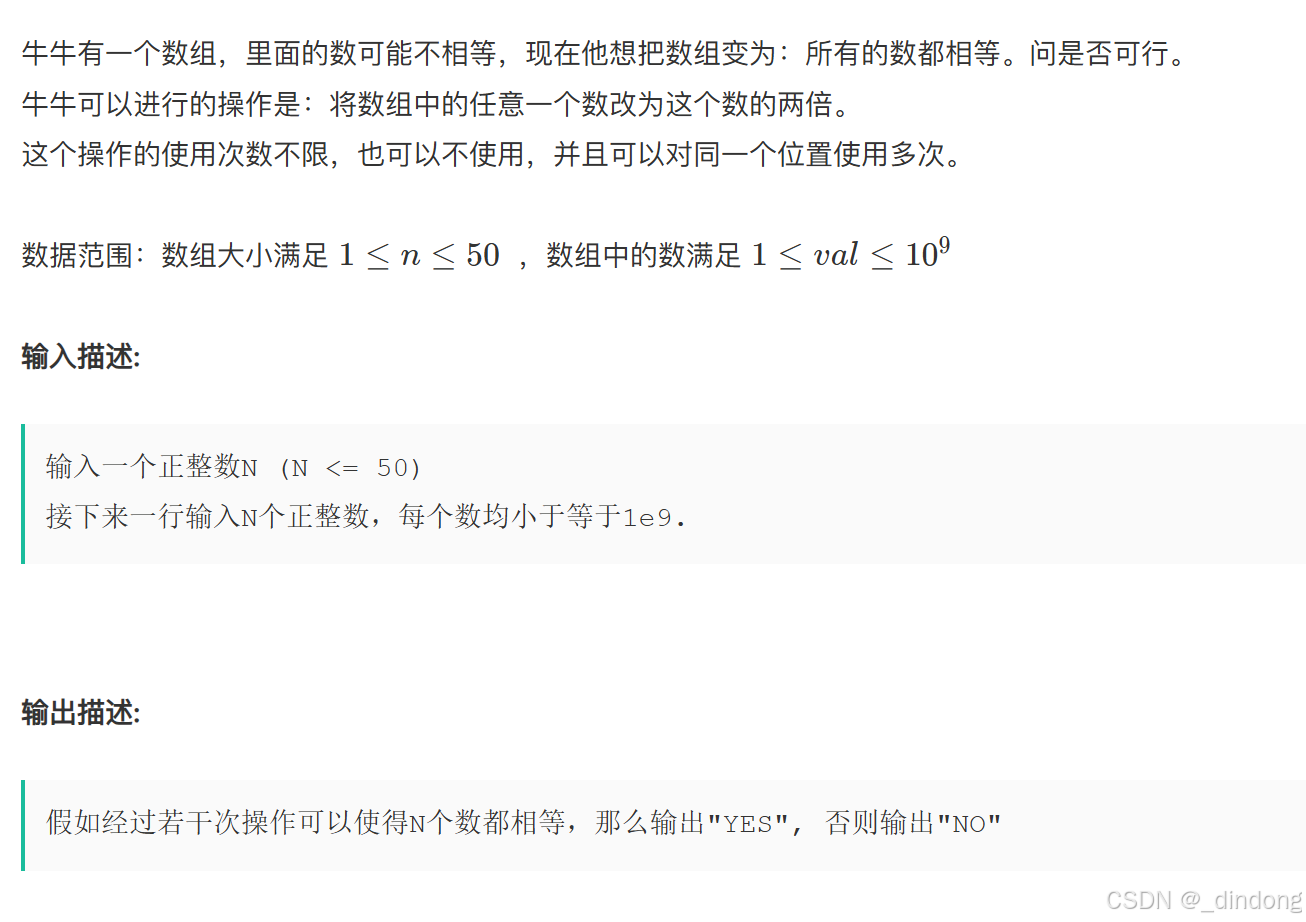
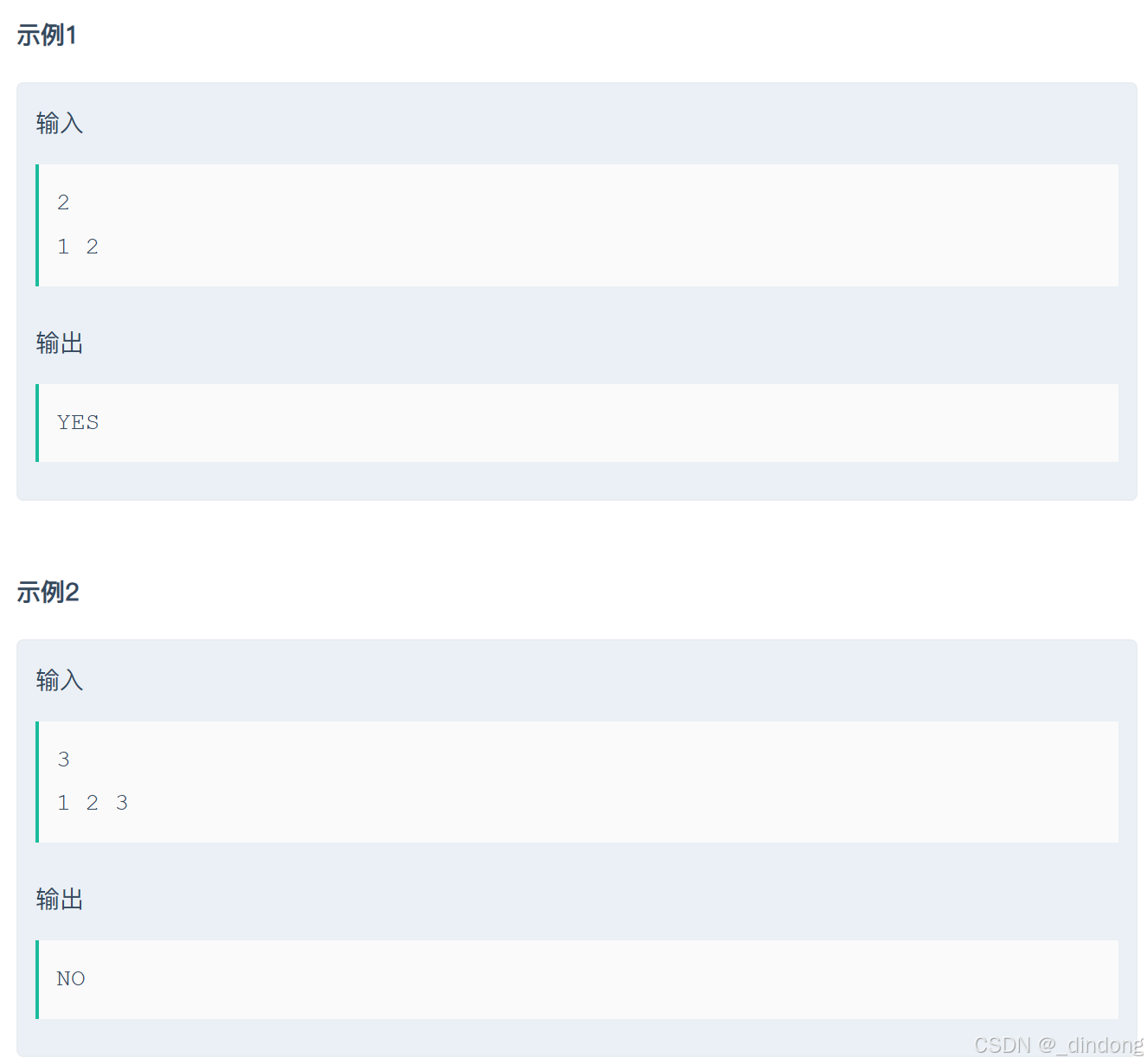
贪心:因为我们每次都需要在一个大一个小的数里面,看小的数不断x2操作能不能达到更大的那个数,因为如果两个数通过乘2操作能相等,那么小的数乘以一定次数的2就能等于大的数。那么现在这个"更大的数"可能会有更大的数,那么就要看这个大的数能不能不断x2操作等于它的更大的数。所以我们只需要找到数组里的最大值,然后看其他数能不能通过x2操作达到这个值即可。那么我们只需要判断MAXNUM/arr[i]能不能被2整除即可。
如何判断被2整除?
x&(x-1)==0就代表最高位是1其他全是0,这就是2的倍数。
或者 x-(x&-x)==0,x&-x得到x低位到高位第一个1,如果减去后为0,就说明只有最高位是1,其他位是0,是2的倍数。
cpp
#include <iostream>
using namespace std;
int a[51];
int n,maxval;
bool func(){
for(int i=0;i<n;++i){
if(maxval%a[i]) return false;
int x=maxval/a[i];
//if(x&(x-1)) return false;
if(x-(x&-x)) return false;
}
return true;
}
int main() {
cin>>n;
for(int i=0;i<n;++i){
cin>>a[i];
maxval=max(maxval,a[i]);
}
cout<<(func()?"YES":"NO")<<endl;
}
// 64 位输出请用 printf("%lld")十二、装箱问题(01背包)

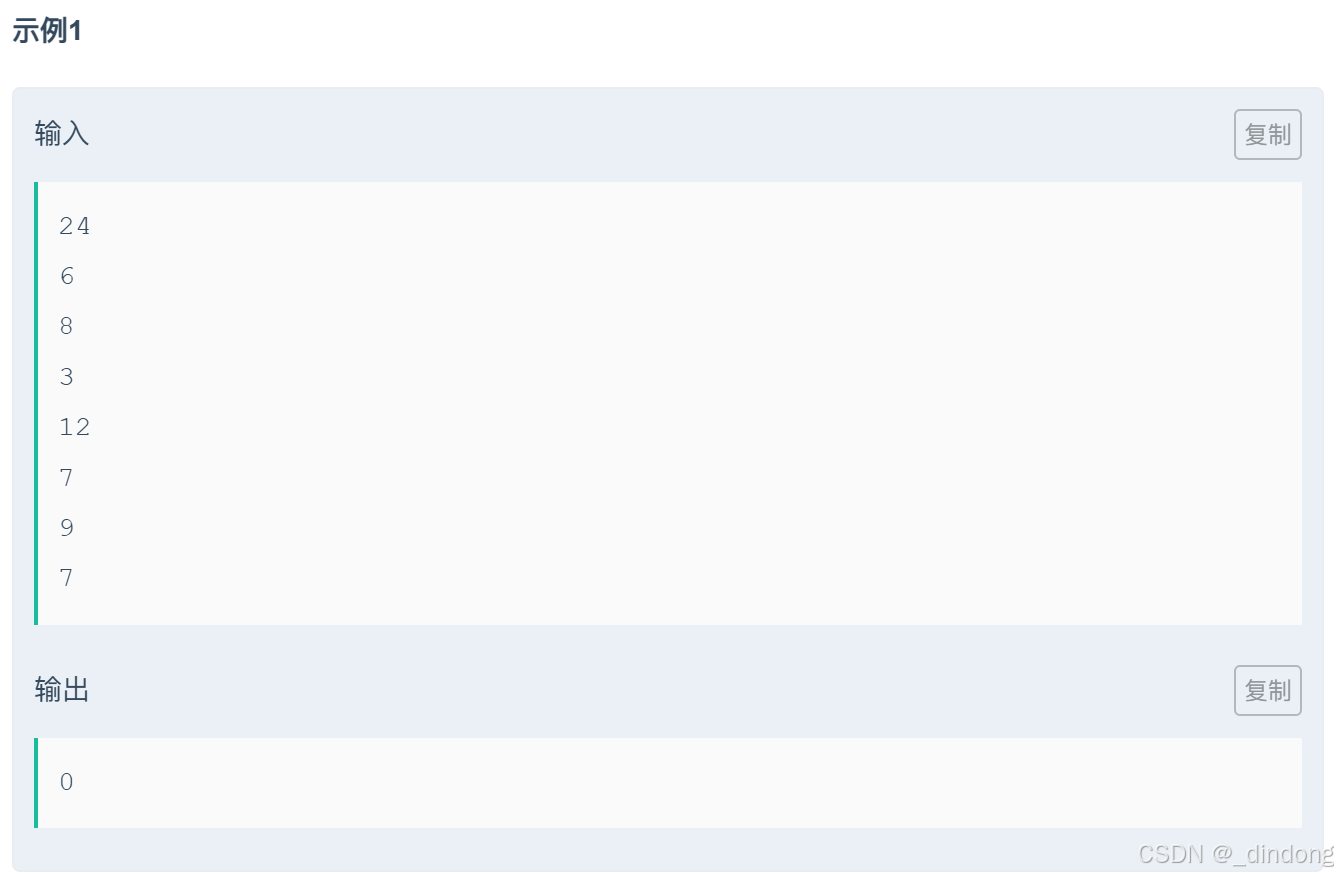
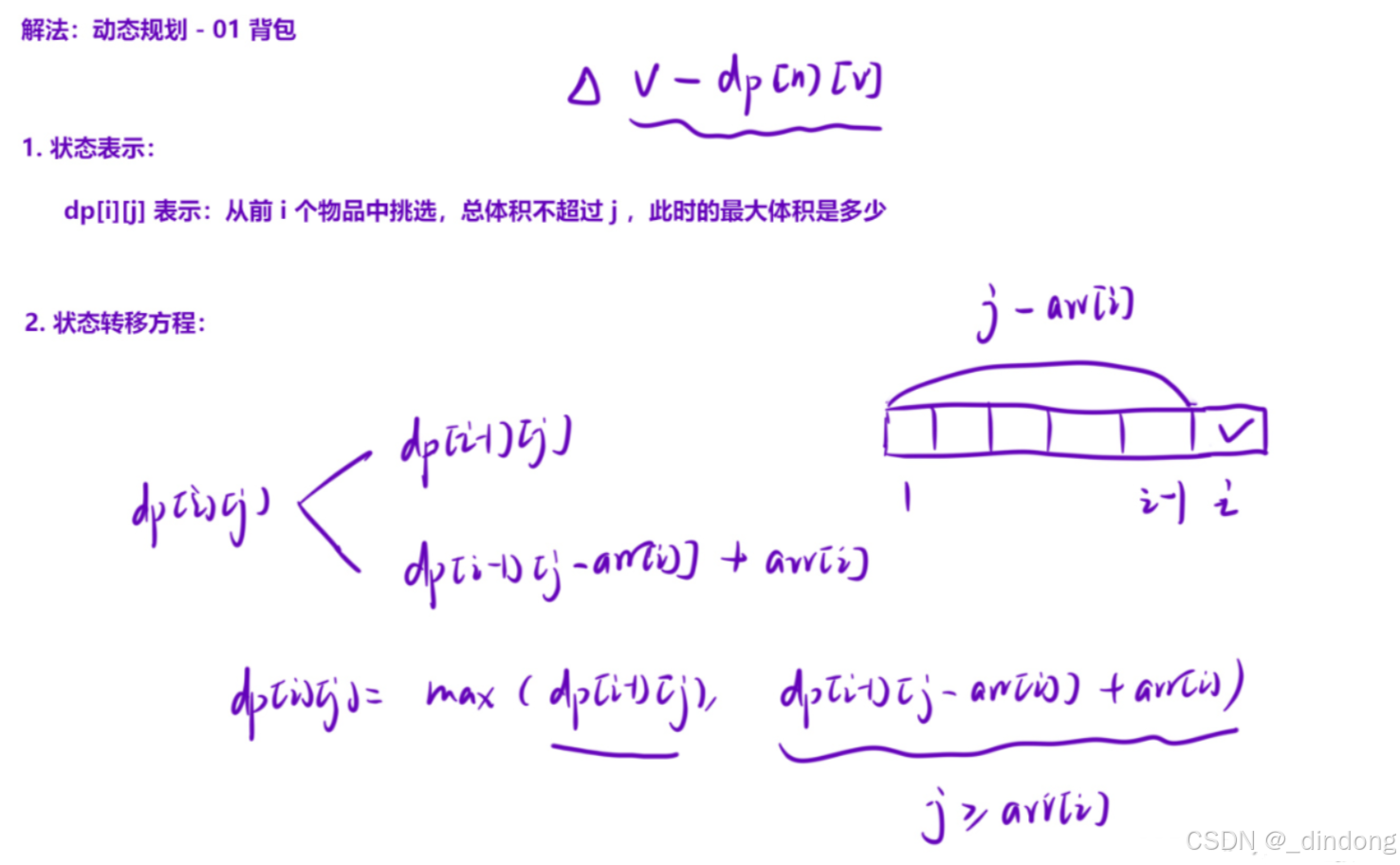
cpp
#include<iostream>
using namespace std;
//dp[i][j]表示选前i个物品 容积不超过j 所占的最大容积
const int N=2e4+1;
int arr[31];
int dp[N];
int v,n;
int main(){
cin>>v>>n;
for(int i=1;i<=n;++i) cin>>arr[i];
for(int i=1;i<=n;++i)
for(int j=v;j>=arr[i];--j)
dp[j]=max(dp[j],dp[j-arr[i]]+arr[i]);
cout<<v-dp[v]<<endl;
}十三*、打怪(模拟+数学)
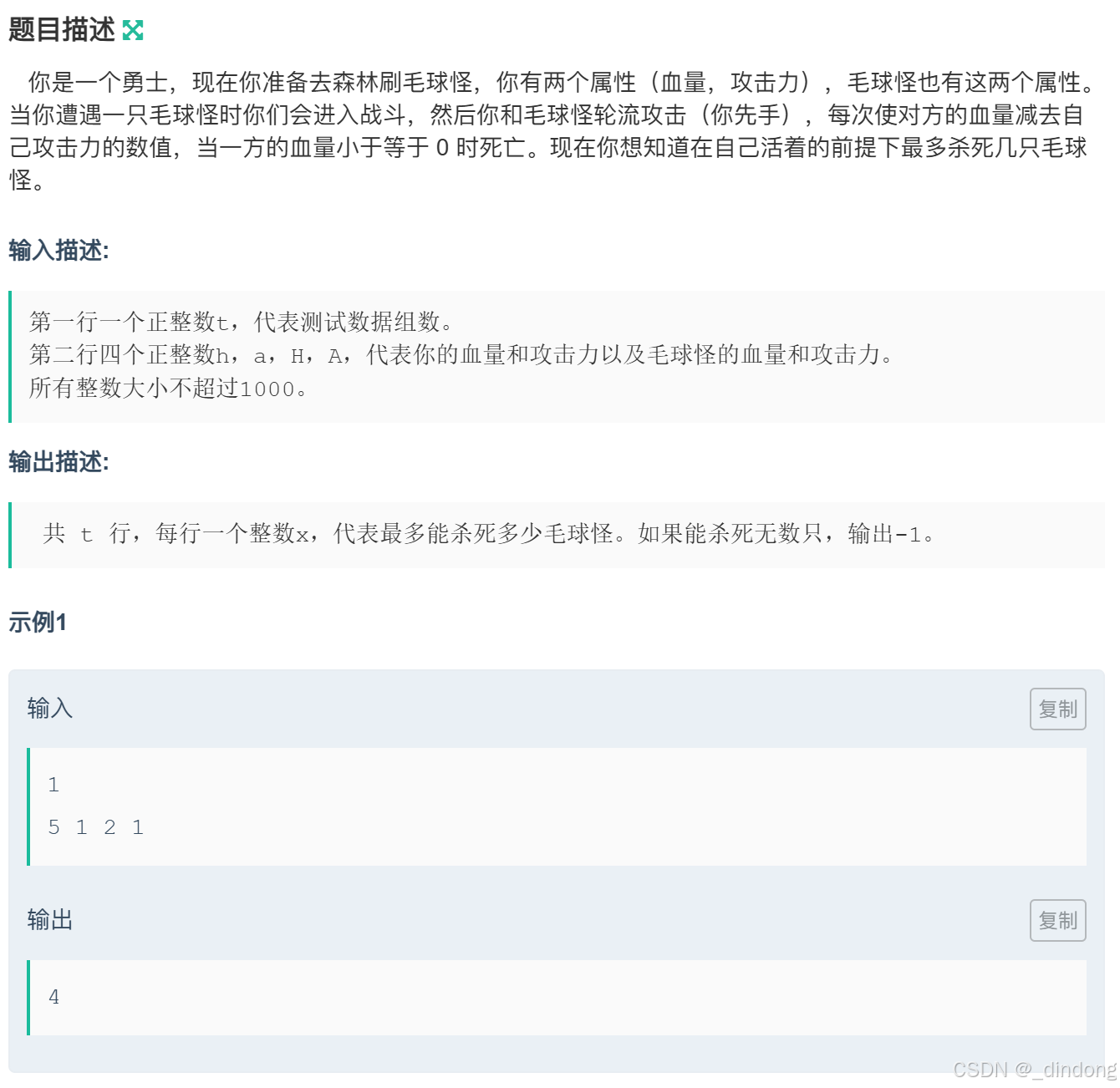
monimonimoni,想这个公式模拟了好久,估计是没睡饱
cpp
#include <iostream>
using namespace std;
int main() {
int t;
cin>>t;
while(t--)
{
int h,a,H,A;
cin>>h>>a>>H>>A;
if(A==0||a>=H){cout<<-1<<endl;continue;}
//times每次杀死怪需要几次攻击
//times-1对应杀死一只怪受到几次伤害
int times=H/a+(H%a?1:0);
//blood是杀一次怪扣的血
//判断最后一次是否符合,如果刚好可以取模,代表第x个怪的时候,勇者先死,减去这一次
int blood=(times-1)*A;
int x=h/blood+(h%blood==0?-1:0);
cout<<x<<endl;
}
return 0;
}十四、字符串分类(排序+哈希)
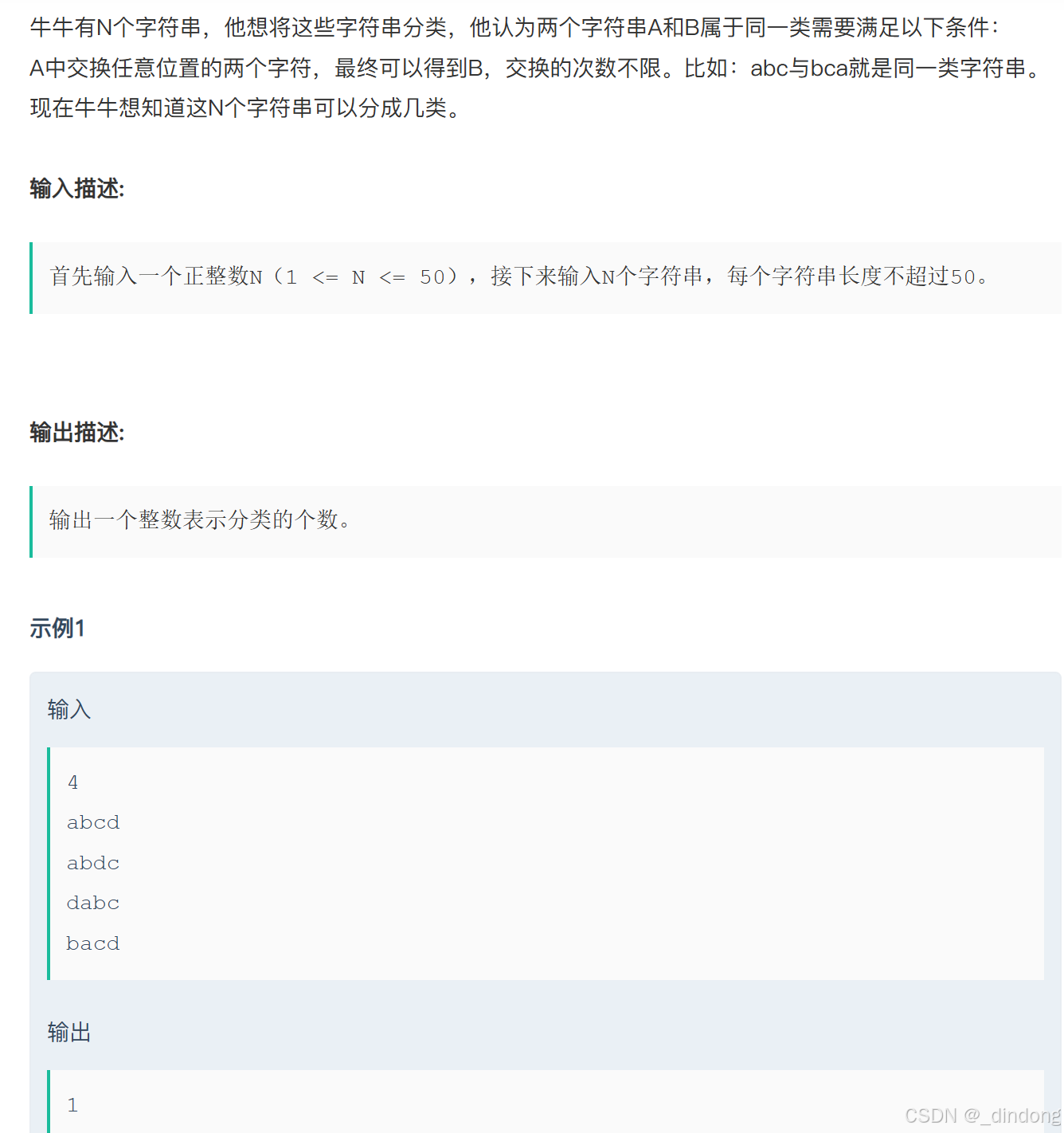
很简单的题目
cpp
#include <iostream>
using namespace std;
#include<algorithm>
#include<unordered_map>
int main() {
int n;
string s;
unordered_map<string, int> hash;
cin>>n;
while(n--)
{
cin>>s;
sort(s.begin(),s.end());
hash[s]++;
}
cout<<hash.size();
return 0;
}十五*、城市群数量(floodfill)

原本以为是遍历下三角,然后统计一下入度,再从1~n里查找入度为0的数量,这样就是城市群的数量。但是这是不正确的。因为:
该题为无向边,没有出度还有入度的概念,所以不能这样统计。
比如2指向1,3指向1,那么此时城市群的数量应该是1.但是按照我们统计入度为0的个数,算出的是2错误
正确解法是floodfill问题的思路,用vis标记连接的城市群
cpp
class Solution {
public:
//联通块问题
bool vis[201]={0};//标记每个城市是否被搜索过
int n;
int citys(vector<vector<int>>& nums) {
n=nums.size();
int ret=0;
for(int i=0;i<n;++i)
if(!vis[i]){
++ret;
dfs(nums,i);//没被搜索过 就从该点开始找联通块
}
return ret;
}
void dfs(vector<vector<int>>& nums,int pos){
vis[pos]=true;
for(int i=0;i<n;++i)
if(!vis[i]&&nums[pos][i]) dfs(nums,i);
}
};今天三道题也是稳稳拿下
十六、判断是不是平衡二叉树(递归)
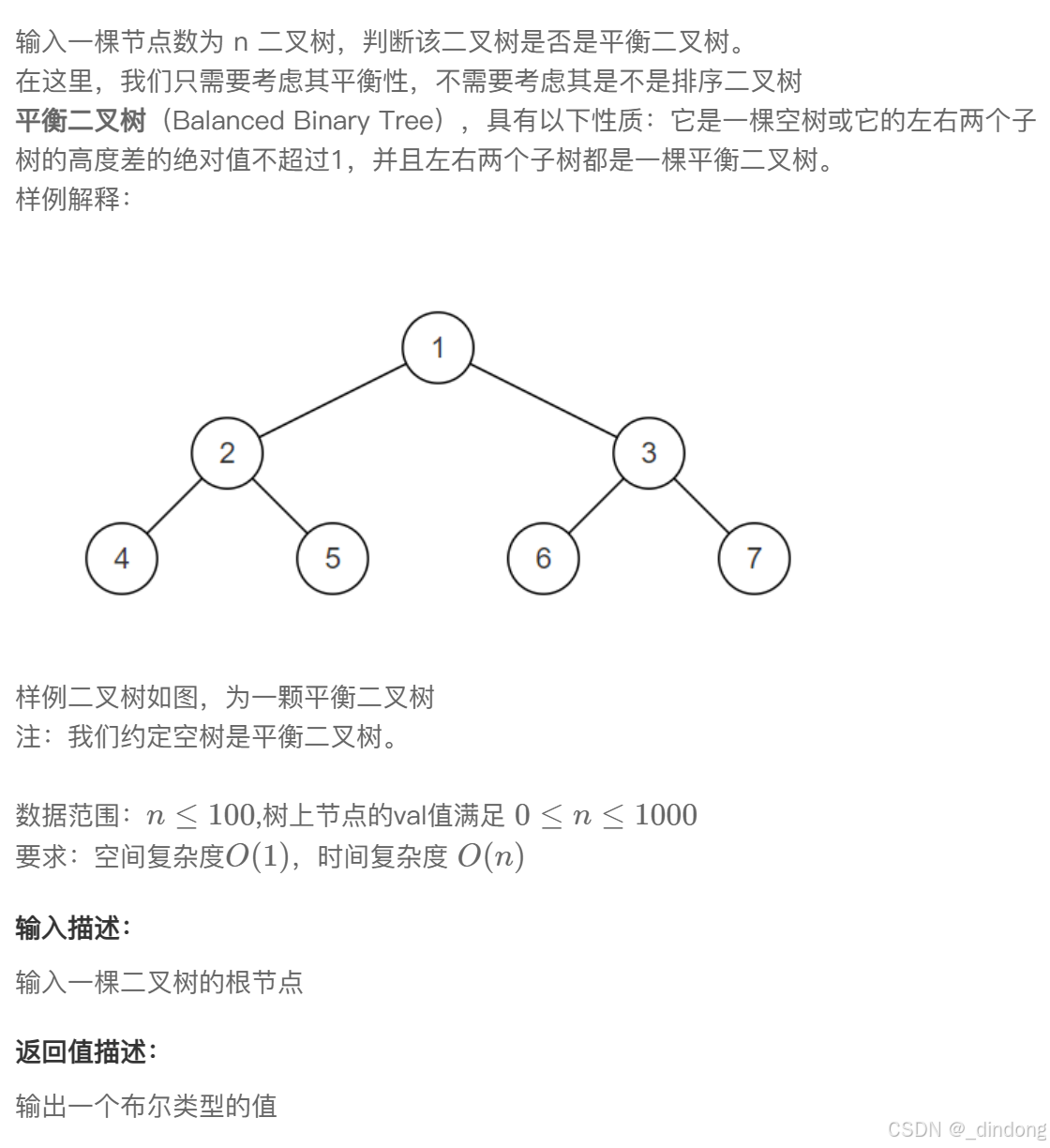
很简单
cpp
class Solution {
public:
int GetDepth(TreeNode*root)
{
if(!root)return 0;
return 1+max(GetDepth(root->left),GetDepth(root->right));
}
bool IsBalanced_Solution(TreeNode* root) {
if(!root)return true;
if(!IsBalanced_Solution(root->left))return false;
if(!IsBalanced_Solution(root->right))return false;
int LeftDepth=GetDepth(root->left),RightDepth=GetDepth(root->right);
if(abs(LeftDepth-RightDepth)>1)return false;
return true;
}
};十七、最大子矩阵(二维前缀和)

一遍过
cpp
#include <climits>
#include <iostream>
using namespace std;
#include<vector>
int main() {
int N;cin>>N;
vector<vector<int>> martix(N+1,vector<int>(N+1));
auto FrontSum=martix;
int res=INT_MIN;
for(int i=1;i<=N;++i)
{
for(int j=1;j<=N;++j)
{
cin>>martix[i][j];
//计算前缀和
FrontSum[i][j]=FrontSum[i-1][j]+FrontSum[i][j-1]-FrontSum[i-1][j-1]+martix[i][j];
res=max(res,FrontSum[i][j]);
for(int x=1;x<=i;++x)
{
for(int y=1;y<=j;++y)
{
//计算区间前缀和
int Sum=FrontSum[i][j]-FrontSum[i][y-1]-FrontSum[x-1][j]+FrontSum[x-1][y-1];
res=max(res,Sum);
}
}
}
}
cout<<res;
return 0;
}十八*、小葱的01串(定长滑动窗口)
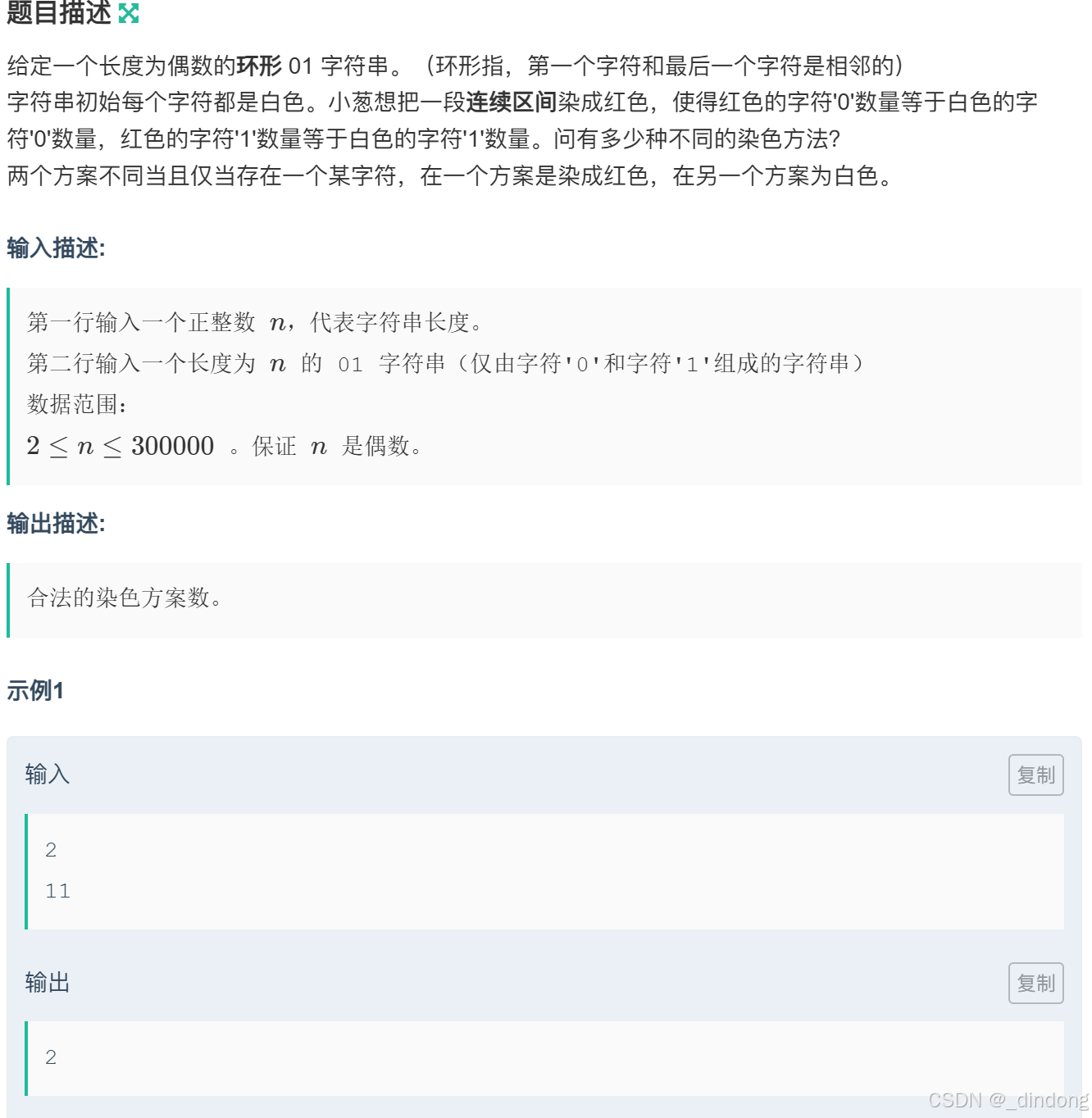
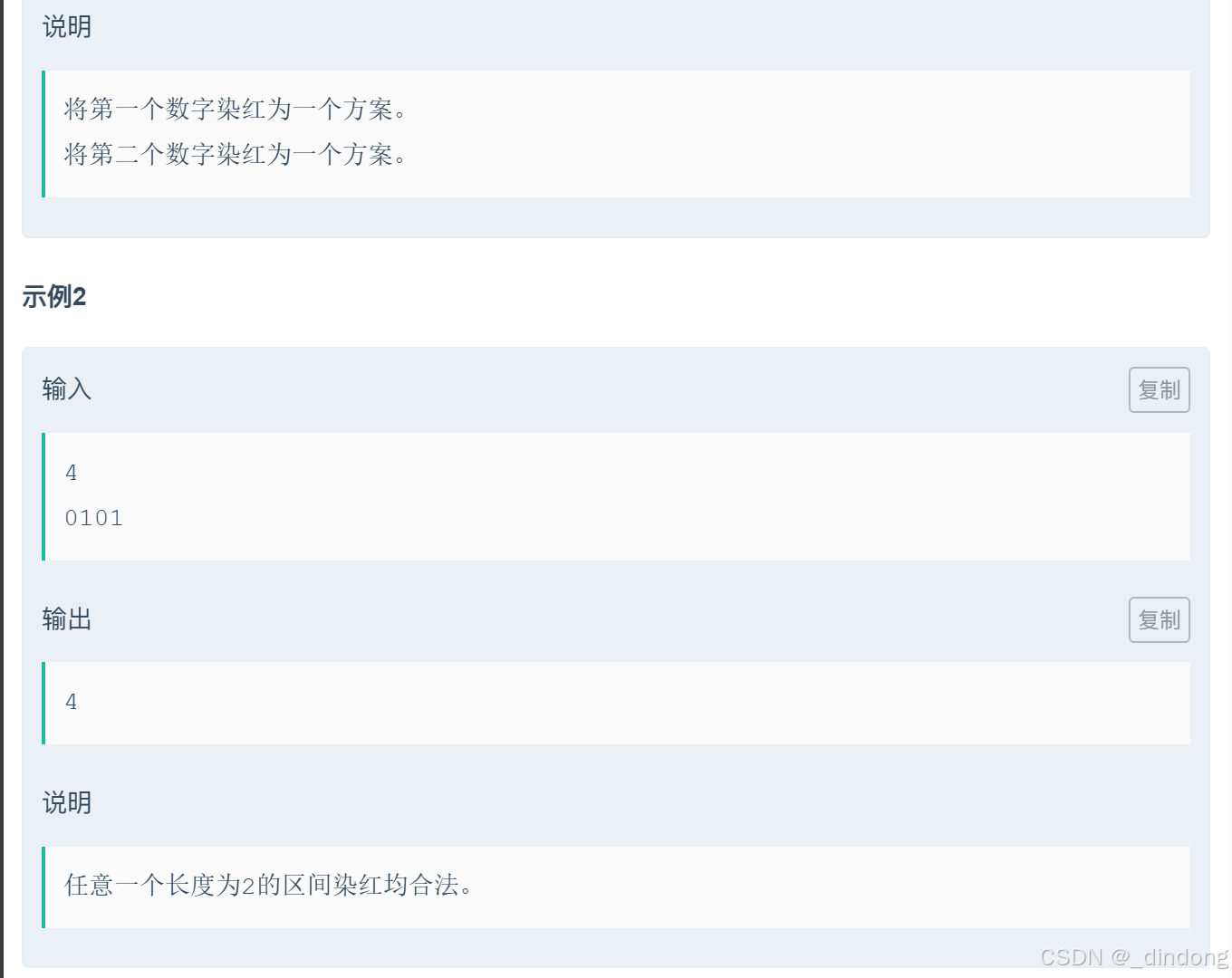

看完题目觉得就是求定长窗口0,1数量如果等于0,1总数的一半就++计数器,然后最后输出计数器乘以2?应该不对,如果头位置和尾位置在窗口里且符合的时候,其实是同一种情况。只有窗口在不包含头尾的中间位置的时候的解决方案才是需要*2的。
cpp
#include <iostream>
using namespace std;
int main() {
int n;cin>>n;
string s;
cin>>s;
int Num0=0,Num1=0,count0=0,count1=0,solves=0;
for(auto&ch:s)
{
if(ch-'0')++Num1;
else ++Num0;
}
for(int i=0;i<n/2;++i)
{
if(s[i]=='0')++count0;
else ++count1;
}
int right=n/2,left=0;
int flag=0;
if(count0==Num0/2&&count1==Num1/2){++solves;flag=2;}
while(right<n)
{
if(s[right]=='0')++count0;
else ++count1;
if(s[left]=='0')--count0;
else --count1;
if(count0==Num0/2&&count1==Num1/2)++solves;
++right;
++left;
}
cout<<(solves-flag)*2+flag;
return 0;
}或者说,因为1和n-1包含在窗口里时是属于同一种情况,我们只需要从0遍历到n-2的位置即可
cpp
#include <iostream>
using namespace std;
int main() {
int n;cin>>n;
string s;
cin>>s;
int Num0=0,Num1=0,count0=0,count1=0,solves=0;
for(auto&ch:s)
{
if(ch-'0')++Num1;
else ++Num0;
}
for(int i=0;i<n/2-1;++i)
{
if(s[i]=='0')++count0;
else ++count1;
}
int left=0,right=n/2-1;
while(right<n-1)
{
if(s[right]=='0')++count0;
else ++count1;
if(count0==Num0/2&&count1==Num1/2)++solves;
if(s[left]=='0')--count0;
else --count1;
++right;
++left;
}
cout<<solves*2;
return 0;
}本周结束!完结撒花✿✿ヽ(°▽°)ノ✿