【算法】递归算法实战：汉诺塔问题详解与代码实现

递归的应用

导读
[一、面试题 08.06.汉诺塔问题](#一、面试题 08.06.汉诺塔问题)
- [1.1 题目介绍](#1.1 题目介绍)
- [1.2 解题思路](#1.2 解题思路)
- [1.3 编写代码](#1.3 编写代码)
- - [1.3.1 定义函数](#1.3.1 定义函数)
  - [1.3.2 寻找递归基](#1.3.2 寻找递归基)
  - [1.3.3 寻找递进关系](#1.3.3 寻找递进关系)
  - [1.3.4 组合优化](#1.3.4 组合优化)
- [1.4 代码测试](#1.4 代码测试)
结语

导读

大家好，很高兴又和大家见面啦！！！

在上一篇内容中，我们系统学习了递归这一重要算法思想的核心要点：

核心概念 ：分而治之------将复杂问题分解为规模更小、形式相同的子问题
实现方法 ：四步法------定义函数→寻找递归基→建立递进关系→组合优化
分析技巧 ：递归树------直观理解执行过程和计算复杂度的有力工具

理论的价值在于指导实践。今天，我们将通过经典的汉诺塔问题，将递归知识付诸实战应用，检验学习成果并提升算法设计能力。

无论你是希望巩固递归这一关键技术点，还是准备应对算法面试挑战，本次实战都将为你提供宝贵的学习经验。

让我们一同开启这段递归思维的深度训练，体验算法设计的精妙之处！

一、面试题 08.06.汉诺塔问题

1.1 题目介绍

相关标签 ：递归、数组
题目难度 ：简单
题目描述 ：

在经典汉诺塔问题中，有 3 根柱子及 N 个不同大小的穿孔圆盘，盘子可以滑入任意一根柱子。

一开始，所有盘子自上而下按升序依次套在第一根柱子上(即每一个盘子只能放在更大的盘子上面)。

移动圆盘时受到以下限制:

每次只能移动一个盘子;
盘子只能从柱子顶端滑出移到下一根柱子;
盘子只能叠在比它大的盘子上。

请编写程序，用栈将所有盘子从第一根柱子移到最后一根柱子。

你需要原地修改栈。

示例 1 ：

输入：A = [2, 1, 0], B = [], C = []

输出：C = [2, 1, 0]

示例 2 ：

输入：A = [1, 0], B = [], C = []

输出：C = [1, 0]

提示：

A 中盘子的数目不大于 14 个。

1.2 解题思路

汉诺塔问题是一个非常经典的递归问题，简单的说，若我们要实现圆盘在不同的柱子间进行移动，那我们就需要合理的利用各根柱子。

根据起始柱 A A A 上的圆盘数的不同，其移动的方式也会有所区别：

当 N == 1 时，即柱 A A A 上有一个圆盘：则我们可以直接将柱 A A A 上的圆盘移动到柱 C C C

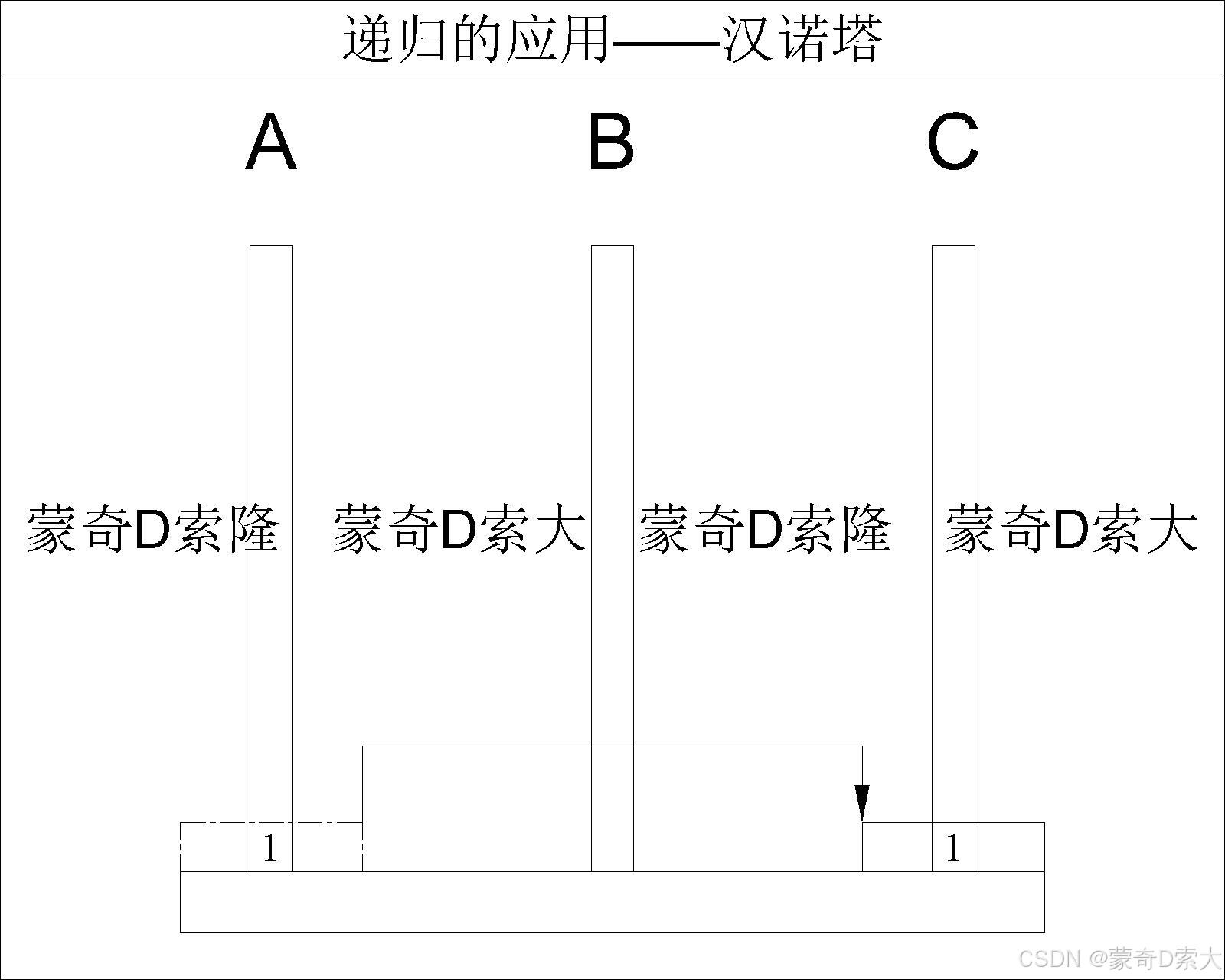
当 N == 2 时，即柱 A A A 上有两个圆盘：我们需要借助柱 B B B 完成将圆盘从柱 A A A 移动到柱 C C C

先将最上面的圆盘移动到柱 B B B

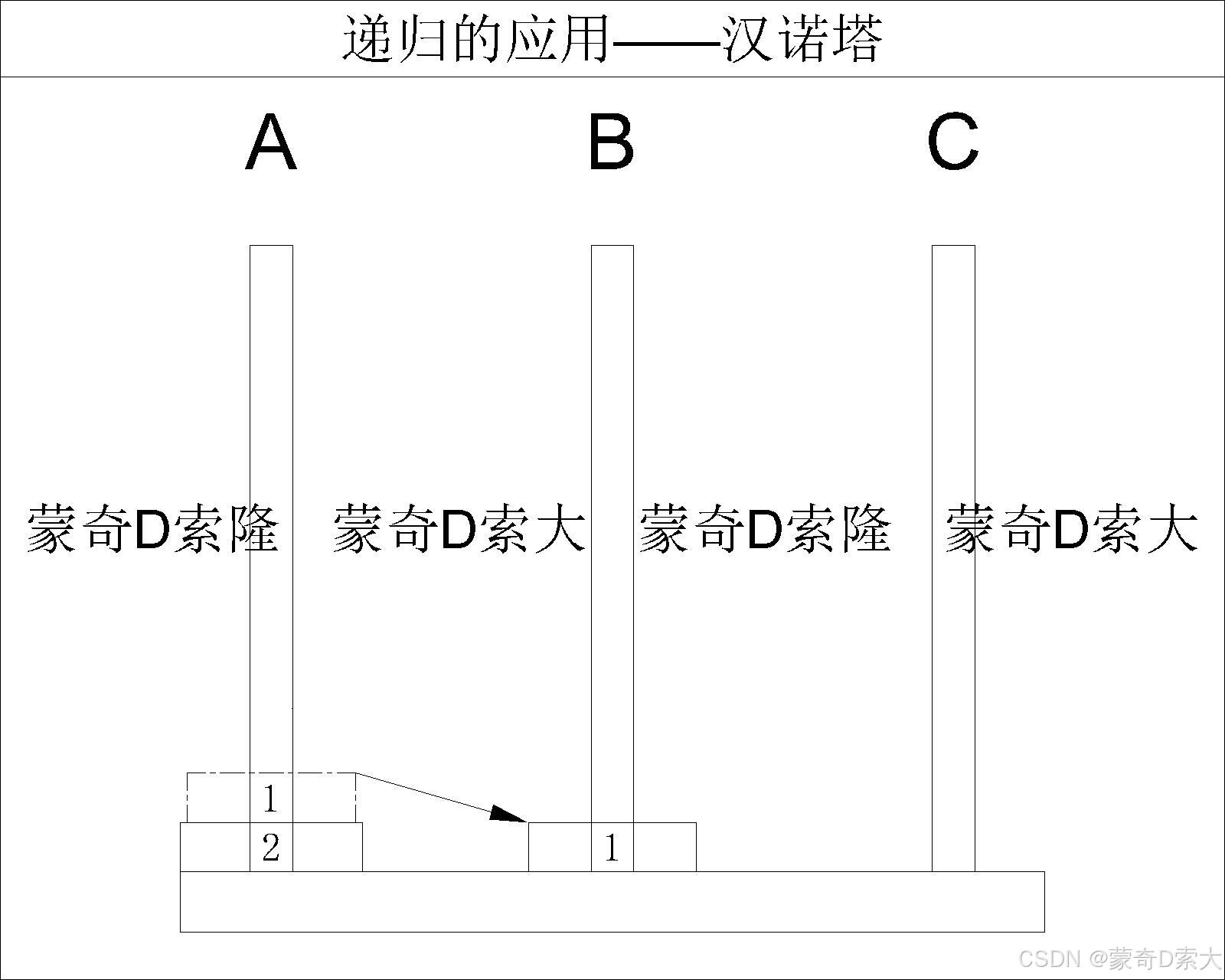
完成移动后，此时柱 A A A 上就只剩下了一个圆盘，这时又回到了 N == 1 的情况，这时我们只需要按照 N == 1 的处理方法执行即可

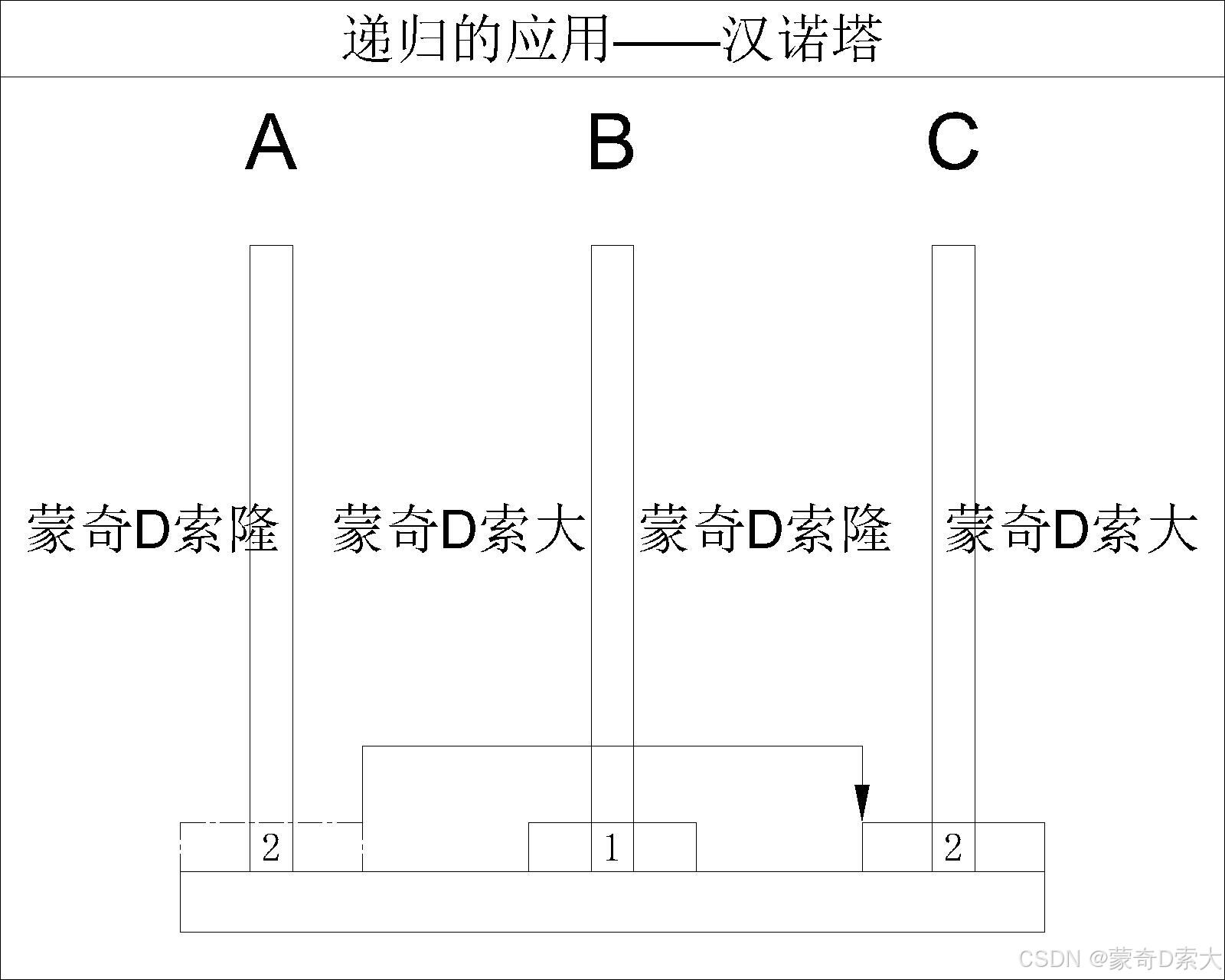
最后我们再将柱 B B B 上的圆盘移动到柱 C C C 上即可；

当 N == 3 时，即柱 A A A 上有三个圆盘：则我们需要先借助柱 C C C 将最上面的两个圆盘从柱 A A A 移动到柱 B B B

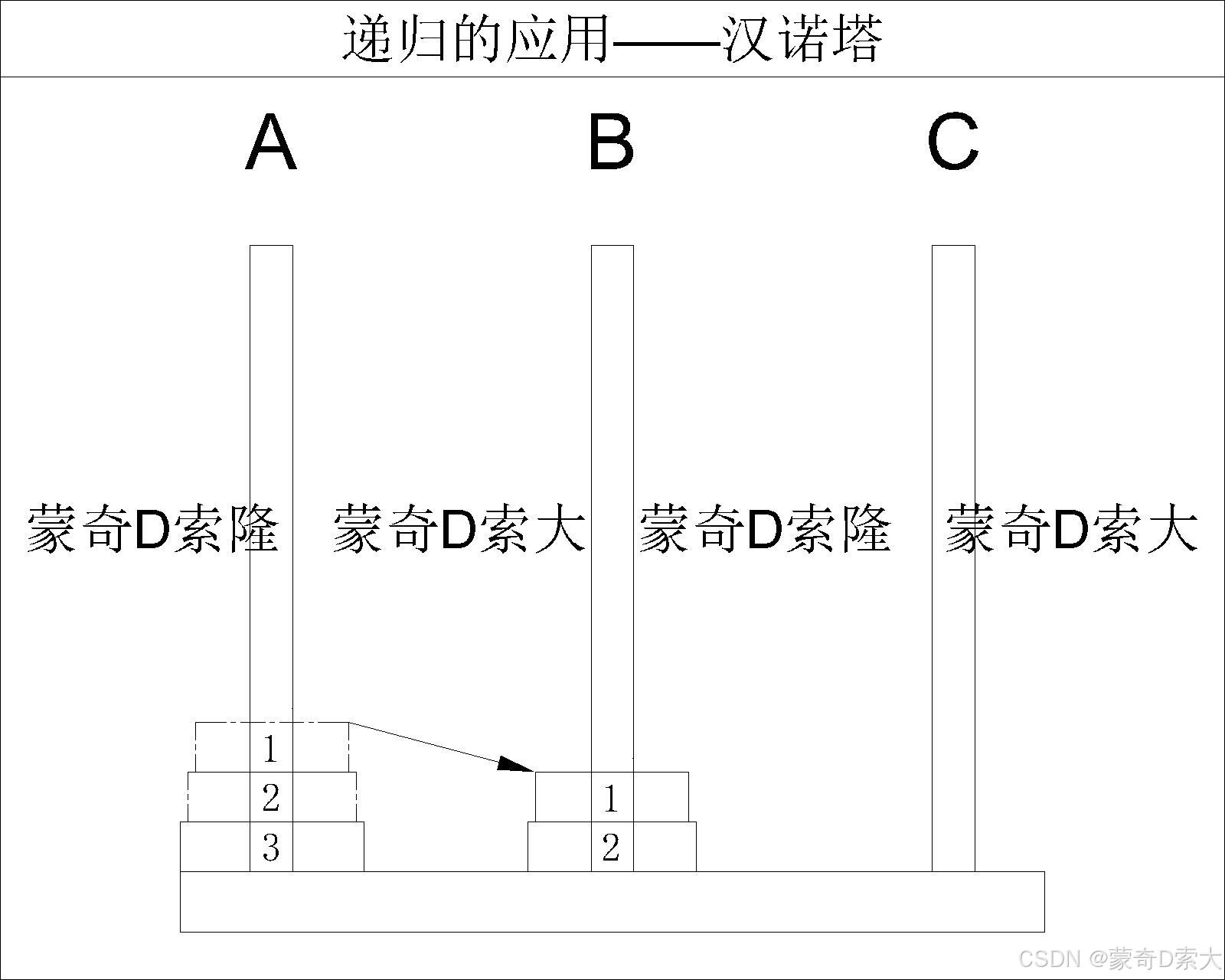
再将最后一个圆盘从柱 A A A 直接移动到柱 C C C

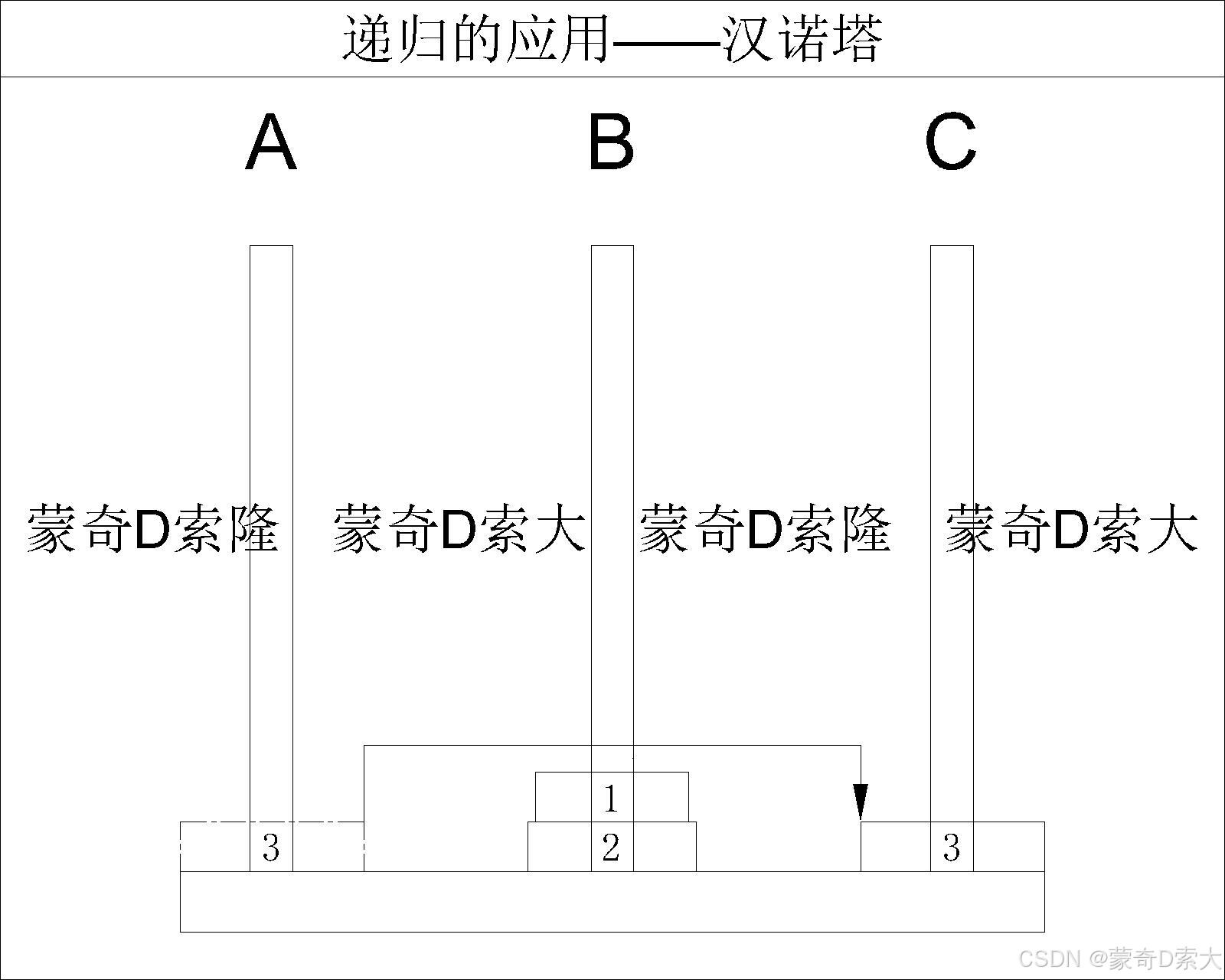
最后再借助柱 A A A 将柱 B B B 上的两个圆盘移动到柱 C C C

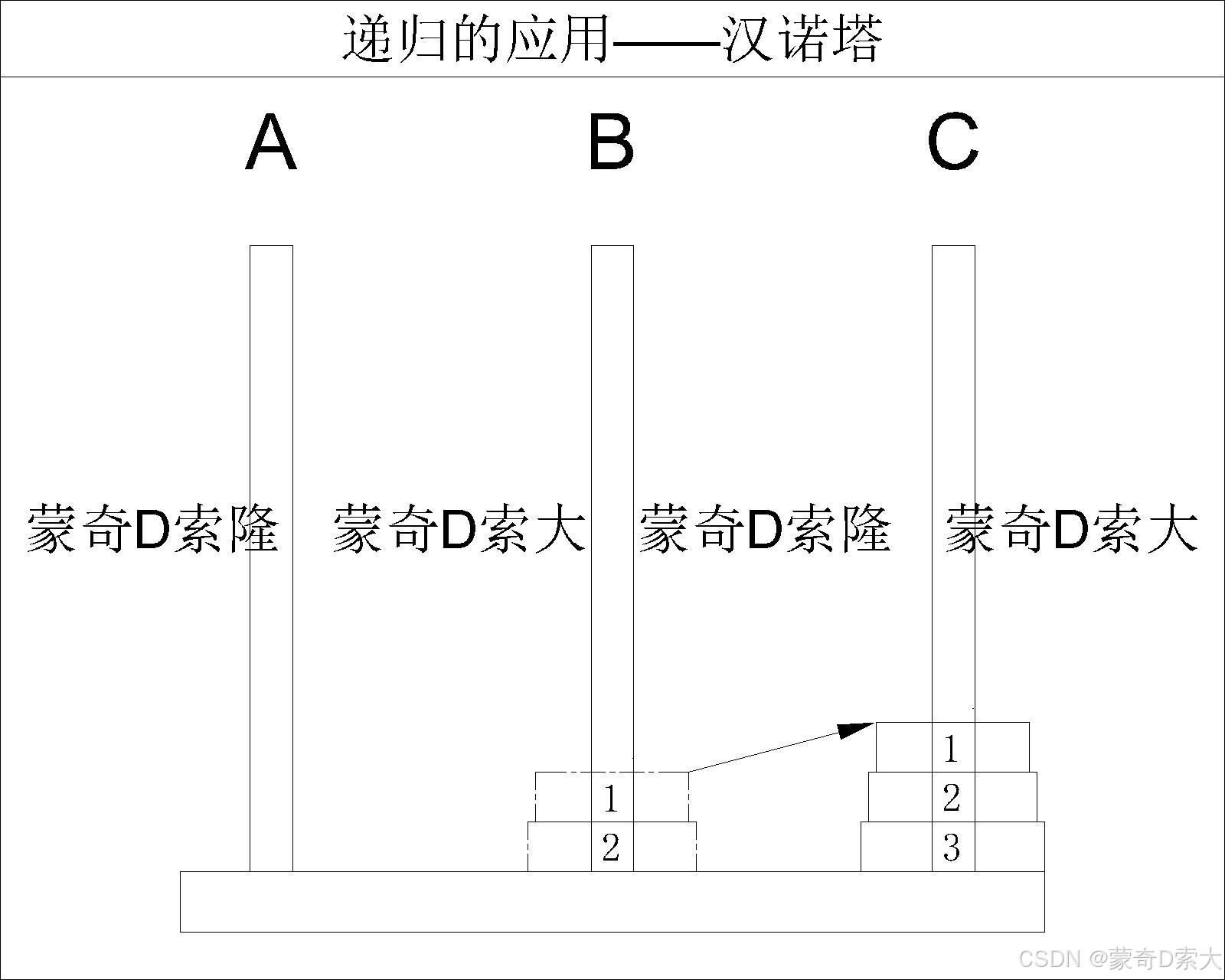
当 N == 4 时，即柱 A A A 上有四个圆盘：先借助柱 C C C 将最上面的三个圆盘从柱 A A A 移动到柱 B B B

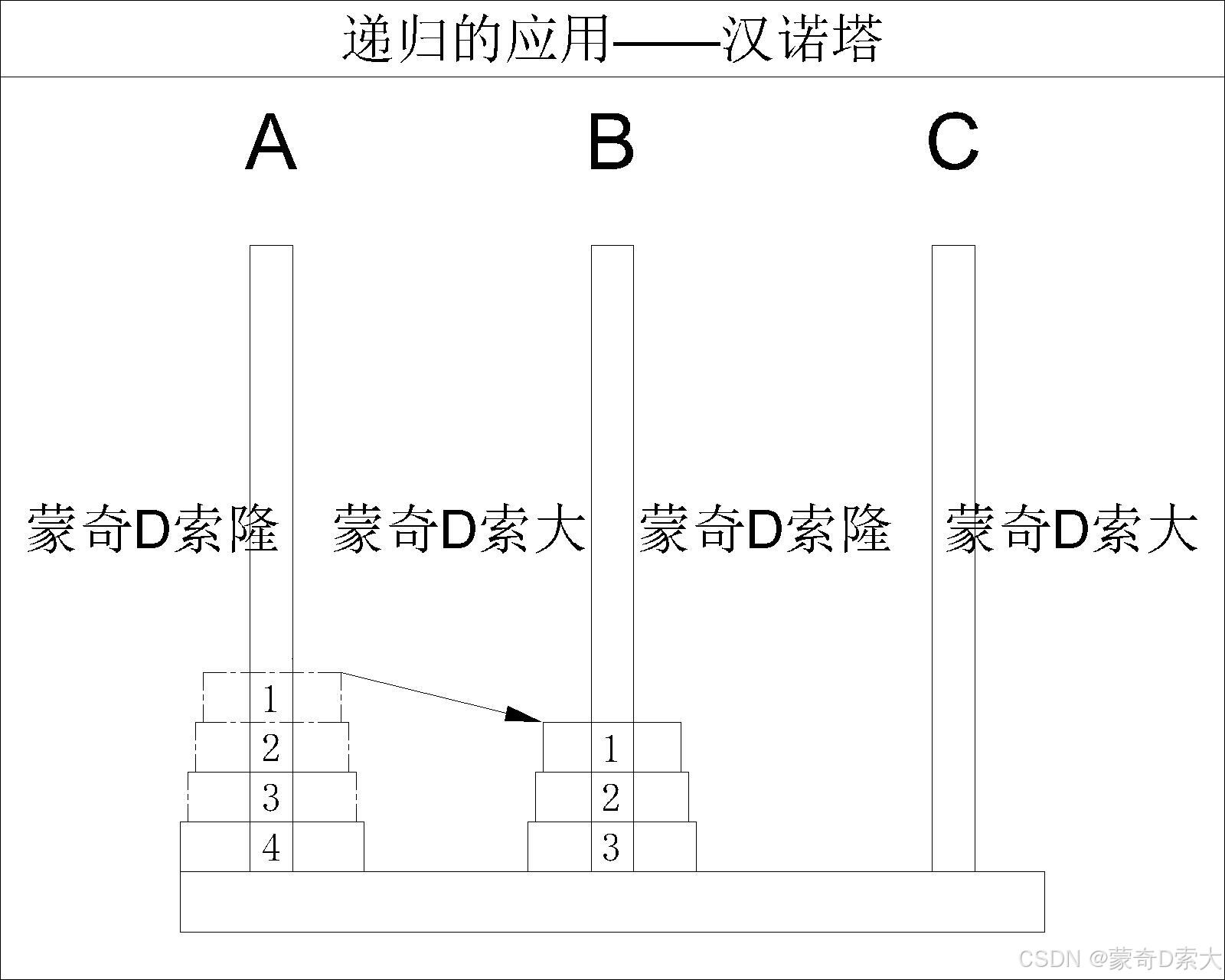
再将柱 A A A 上的最后一个圆盘移动至柱 C C C

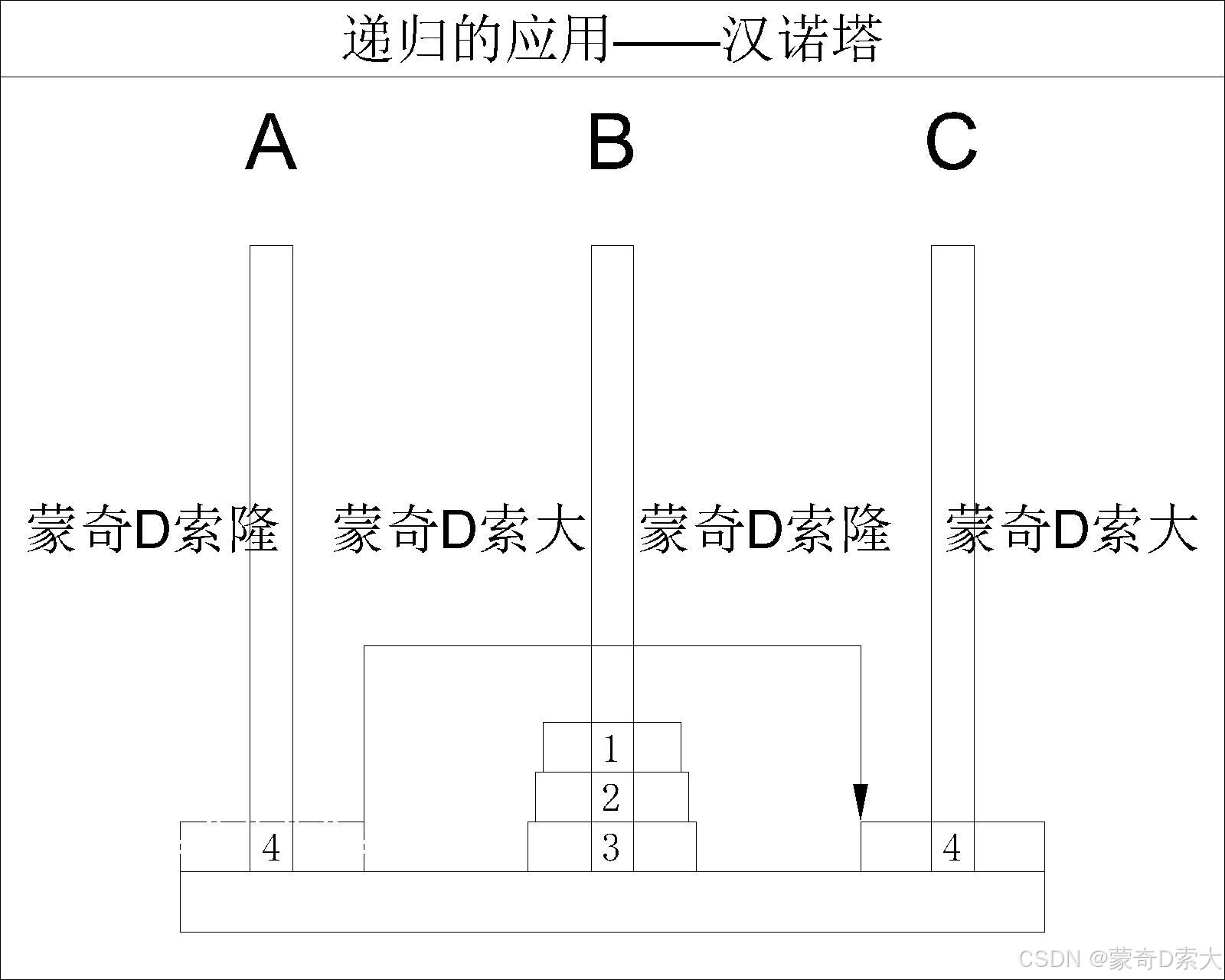
最后再借助柱 A A A 将柱 B B B 上的三个圆盘移动到柱 C C C

从这里我们不难看出，当我们将柱 A A A 上的圆盘分为两部分：前 n − 1 n - 1 n−1 个圆盘以及第 n n n 个圆盘后，整个移动过程我们可以总结为三步：

借助柱 C C C 将前 n − 1 n - 1 n−1 个圆盘从柱 A A A 移动到柱 B B B
将第 n n n 个圆盘从柱 A A A 移动到柱 C C C
借助柱 A A A 将前 n − 1 n - 1 n−1 个圆盘从柱 B B B 移动到柱 C C C

1.3 编写代码

1.3.1 定义函数

汉诺塔的函数名我们可以直接使用 Hnt ；

函数的参数我们根据思路分析可以得出参数至少需要4个：

起始柱：src
过渡柱：mid
目标柱：des
移动的圆盘数：num

汉诺塔函数要实现的功能可以总结为：

将 num 个圆盘借助 mid 从 src 柱移动到 des 柱

因此汉诺塔并不需要任何返回值，即其函数的返回类型为 void：

c 复制代码

void Hnt(int* src, int* mid, int* des, int num){

}

1.3.2 寻找递归基

从解题思路中我们不难看出，当 A A A 柱上的圆盘数量只有 1 1 1 个时，函数只需要执行一步操作------将圆盘从柱 A A A 移动到柱 C C C。

若我们将该情况做一个简单的处理------将 N == 1 的情况视为两部分：

第一部分为前 0 0 0 个圆盘
第二部分为第 1 1 1 个圆盘

此时我们同样执行的是三步：

将前 0 0 0 个圆盘借助 C C C 柱从 A A A 柱移动到 B B B 柱
将第 1 1 1 个圆盘从 A A A 柱移动到 B B B 柱
将前 0 0 0 个圆盘借助 A A A 柱从 B B B 柱移动到 C C C 柱

那此时我们又可以得出一个结论：

当 N == 0 时，函数不执行任何操作

因此，这里我们直接以 num == 0 作为递归基：

c 复制代码

if (num == 0) {
	return;
}

1.3.3 寻找递进关系

函数的递进关系同样由 num 决定，这里我们可以将 num 分为两部分：

前 num - 1 个圆盘
第 num 个圆盘

在移动的过程中，我们将这两部分的圆盘需要完成三次移动：

前 num - 1 个圆盘借助 des 柱从 src 柱移动到 mid 柱
第 num 个圆盘从 src 柱移动到 des 柱
前 num - 1 个圆盘借助 src 柱从 mid 柱移动到 des 柱

其对应的代码为：

c 复制代码

	Hnt(src, des, mid, num - 1);
	move(src, des, 1);
	Hnt(mid, src, des, num - 1);

具体的移动过程我们可以通过删除与添加操作完成：

从 src 删除该圆盘
将该圆盘添加到 des

c 复制代码

void move(int* src, int* des, int num) {
	Insert(des, src[0]);
	Delete(src, src[0]);
}

1.3.4 组合优化

现在我们对汉诺塔问题的递归算法整体框架就已经完成了：

c 复制代码

void move(int* src, int* des, int num) {
	Insert(des, src[0]);
	Delete(src, src[0]);
}
void Hnt(int* src, int* mid, int* des, int num) {
	if (num == 0) {
		return;
	}
	Hnt(src, des, mid, num - 1);
	move(src, des, 1);
	Hnt(mid, src, des, num - 1);
}

接下来为了能够更好的完成该算法，我们需要对其仅一下整体的优化；

数据结构优化

汉诺塔的实际操作过程是以栈完成，因此在不改变原数组的情况下，我们可以通过栈顶指针来指向 A/B/C 这三个栈的栈顶元素；

ASize 指向栈 A 的栈顶元素的下一个元素
BSize 指向栈 B 的栈顶元素的下一个元素
CSize 指向栈 C 的栈顶元素的下一个元素

函数参数优化

函数的具体参数我们可以直接采用 leetcode 中提供的参数：

int* A：栈 A 的数组空间
int ASize：栈 A 的栈顶指针
int* B：栈 B 的数组空间，需要主动申请内存空间
int BSize：栈 B 的栈顶指针
int** C：栈 C 的数组空间，需要主动申请内存空间
int *CSize：栈 C 的栈顶指针
int num：移动的元素个数

移动优化

在移动函数中，我们是通过对原栈的栈顶元素进行出栈，对目标栈的栈顶元素进行入栈：

c 复制代码

void move(int* A, int* ASize, int* C, int* CSize) {
	C[*CSize] = A[*ASize - 1];
	*CSize += 1;
	*ASize -= 1;
}

最后我们将完成了优化后的内容进行组合，就得到了最终的代码：

c 复制代码

void move(int* A, int* ASize, int* C, int* CSize) {
	C[*CSize] = A[*ASize - 1];
	*CSize += 1;
	*ASize -= 1;
}
void Hnt(int* A, int* ASize, int* B, int* BSize, int* C, int* CSize, int num) {
	if (num == 0) {
		return;
	}
	Hnt(A, ASize, C, CSize, B, BSize, num - 1);
	move(A, ASize, C, CSize);
	Hnt(B, BSize, A, ASize, C, CSize, num - 1);
}

void hanota(int* A, int ASize, int* B, int BSize, int** C, int* CSize) {
	B = (int*)calloc(ASize, sizeof(int));
	assert(B);
	*C = (int*)calloc(ASize, sizeof(int));
	assert(*C);
	*CSize = 0;
	Hnt(A, &ASize, B, &BSize, *C, CSize, ASize);
	free(B);
	B = NULL;
}

1.4 代码测试

下面我们就在 leetcode 中对代码进行提交测试：

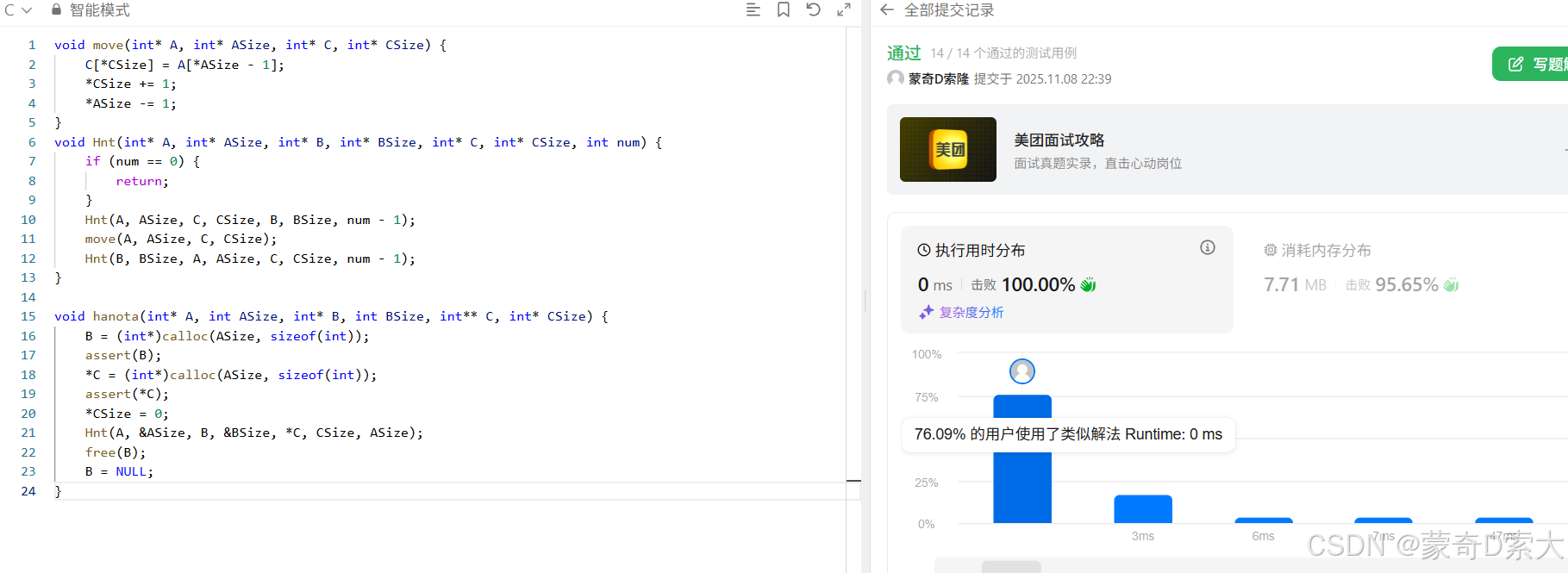
可以看到，此时我们就很好的通过递归解决了汉诺塔问题；

结语

通过本次对汉诺塔问题的深入剖析与实战编码，我们成功地将递归理论应用于具体问题解决中。让我们回顾一下本次学习的重要收获：

🎯 核心收获

递归思维的应用：通过"分而治之"思想，将复杂的汉诺塔问题分解为可管理的子问题
四步法的实战验证：从函数定义到递归基确定，再到递进关系建立，最后进行组合优化，完整展现了递归算法的构建过程
问题抽象能力提升：学会了如何将实际问题转化为递归模型，这是算法设计的关键技能

💡 递归的威力

汉诺塔问题完美展示了递归算法的优雅与强大------仅仅十余行代码就能解决看似复杂的多层圆盘移动问题。这正是递归的魅力所在：用简洁的代码表达复杂的逻辑。

🚀 下一步学习建议

掌握了汉诺塔这个经典案例后，建议你可以继续探索：

快速幂算法（pow(x, n)） - 体验递归在数学计算中的高效应用
其他递归经典问题（如斐波那契数列、二叉树遍历等）
递归的时间复杂度分析方法
递归与迭代的转换技巧

递归作为算法设计的基石，其重要性不言而喻。希望本次实战能帮助你建立对递归的直观感受和深刻理解，为后续的算法学习打下坚实基础。

互动与分享

点赞👍 - 您的认可是我持续创作的最大动力
收藏⭐ - 方便随时回顾这些重要的基础概念
转发↗️ - 分享给更多可能需要的朋友
评论💬 - 欢迎留下您的宝贵意见或想讨论的话题

感谢您的耐心阅读！关注博主，不错过更多技术干货。我们下一篇再见！