计算机视觉是一个分析图像和视频的广阔领域。虽然很多人一听到计算机视觉,首先想到的通常是机器学习模型,但实际上,还有很多其他现有算法,在某些情况下,它们表现得比人工智能还要好!
在计算机视觉中,特征检测 这个领域主要关注的是识别图像中独特的感兴趣区域。这些结果随后可以用来创建特征描述符------即代表局部图像区域的数值向量。之后,可以将同一场景的多张照片的特征描述符组合起来,进行图像匹配,甚至重建场景。
在本文中,我们将借助微积分的类比,来介绍图像导数和梯度。这对于我们理解卷积核,特别是Sobel算子------一种用于检测图像边缘的计算机视觉滤波器------背后的逻辑是必要的。
图像强度
强度是图像的主要特征之一。图像的每个像素都有三个分量:R(红)、G(绿)和B(蓝),它们的取值在0到255之间。值越高,像素越亮。一个像素的强度其实就是其R、G、B分量的加权平均值。
实际上,存在几种定义不同权重的标准。公式如下所示:
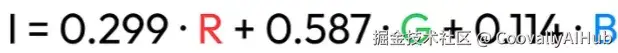
ini
import cv2
import numpy as np
image = cv2.imread('image.png')
B, G, R = cv2.split(image)
grayscale_image = 0.299 * R + 0.587 * G + 0.114 * B
grayscale_image = np.clip(grayscale_image, 0, 255).astype('uint8')
intensity = grayscale_image.mean()
print(f"图像强度: {intensity:.2f}")- 灰度图像
图像可以用不同的色彩通道来呈现。如果RGB通道代表原始图像,那么应用上面的强度公式会将其转换为灰度格式,这种格式只包含一个通道。
由于公式中的权重之和等于1,灰度图像的强度值也将介于0到255之间,就像RGB通道一样。

RGB通道可以使用cv2.cvtColor()函数转换为灰度格式,这比我们上面看到的方法更简便。
ini
image = cv2.imread('image.png')
grayscale_image = cv2.cvtColor(image, cv2.COLOR_BGR2GRAY)
intensity = grayscale_image.mean()
print(f"图像强度: {intensity:.2f}")如果我们用这两种方法计算图像强度,可能会得到略有不同的结果。这完全正常,因为在使用cv2.cvtColor函数时,OpenCV会将转换后的像素值四舍五入到最接近的整数。计算平均值时会导致微小的差异。
图像导数
图像导数用于衡量像素强度在图像中变化的速度。图像可以被看作是一个关于两个参数(x, y)的函数 I(x, y),其中x和y指定了像素位置,I代表该像素的强度。
我们可以形式化地写成:
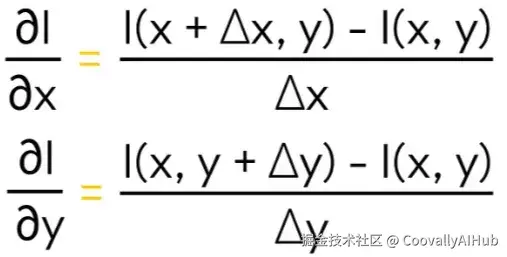
但考虑到图像存在于离散空间中,它们的导数通常通过卷积核来近似计算:
- 对于水平X轴:使用核 [-1, 0, 1]
- 对于垂直Y轴:使用核 [-1, 0, 1]ᵀ (转置)
换句话说,我们可以将上面的方程重写为以下形式(其中 Δx = 1, Δy = 1):

为了更好地理解卷积核背后的逻辑,让我们参考下面的例子。
假设我们有一个5x5像素的矩阵,代表一个灰度图像块。这个矩阵的元素显示了像素的强度。
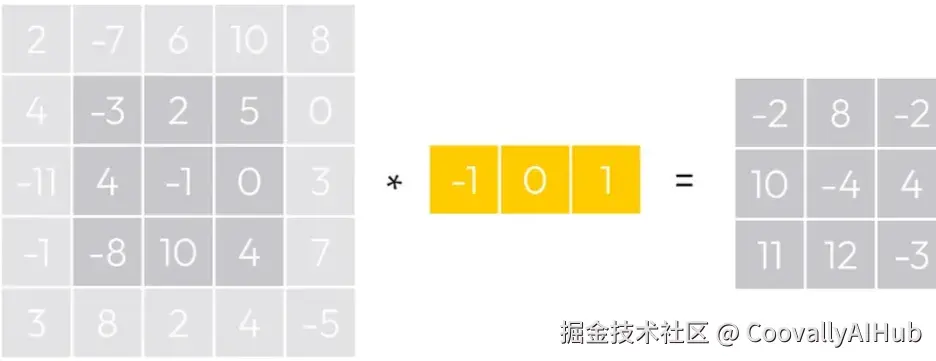
为了计算图像导数,我们可以使用卷积核。思路很简单:选取图像中的一个像素及其邻域内的几个像素,将它们与一个给定的核(代表一个固定的矩阵或向量)进行元素级的乘法,然后求和。
在我们的例子中,我们将使用一个三元素向量 [-1, 0, 1]。从上面的例子中,我们取位置在 (1, 1) 的像素,其值为 -3。
由于(黄色的)核大小是3x1,我们需要-3的左边和右边的元素来匹配这个大小,因此我们取向量 [4, -3, 2]。
然后,通过计算元素乘积之和,我们得到值 -2:

这个-2的值代表了初始像素的导数。如果我们仔细观察,会发现像素-3的导数其实就是它右边像素(2)和左边像素(4)的差值。
既然我们可以直接计算两个元素的差,为什么还要用复杂的公式呢?确实,在这个例子中,我们本可以只计算元素 I(x, y+1) 和 I(x, y-1) 的强度差。但在现实中,当我们需要检测更复杂、更不明显的特征时,可以处理更复杂的场景。因此,使用核的泛化形式是很方便的,这些核的矩阵对于检测预定义类型的特征是已知的。
根据导数值,我们可以做一些观察:
- 如果某个图像区域的导数值很大,意味着那里的强度发生了剧烈变化。否则,在亮度方面没有明显变化。
- 如果导数值为正,意味着从左到右,图像区域变亮;如果为负,则意味着从左到右,图像区域变暗。
通过与线性代数类比,核可以被看作是对图像进行操作的线性算子,它们能转换局部图像区域。
类似地,我们可以计算与垂直核的卷积。步骤保持不变,只是我们现在将我们的窗口(核)在图像矩阵上垂直移动。
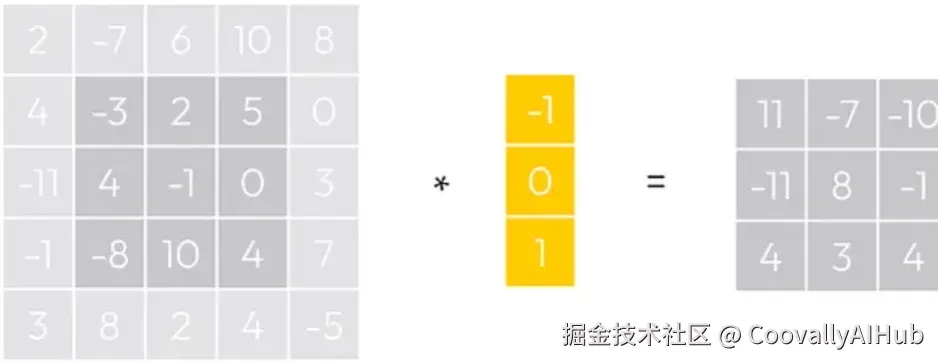
你可能注意到,在将卷积滤波器应用到原始的5x5图像后,它变成了3x3。这是正常的,因为我们无法以同样的方式对边缘像素应用卷积(否则会越界)。
为了保持图像的维度,通常使用填充技术,这包括临时扩展/插值图像边界或用零填充,这样也可以为边缘像素计算卷积。
默认情况下,像OpenCV这样的库会自动填充边界,以确保输入和输出图像具有相同的维度。
图像梯度
图像梯度显示了在给定像素点上,强度(亮度)在两个方向(X和Y)上变化的快慢。
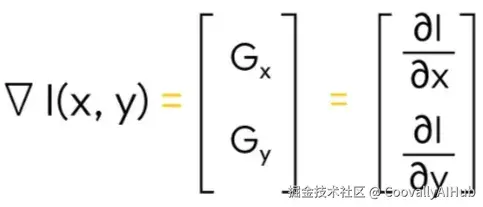
形式上,图像梯度可以写成关于X轴和Y轴的图像导数的向量。
- 梯度幅度
梯度幅度代表了梯度向量的模(范数),可以使用以下公式计算:
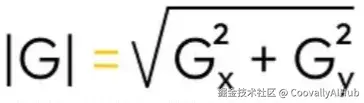
- 梯度方向
使用找到的 Gx 和 Gy,也可以计算梯度向量的角度:

让我们看看如何基于上面的例子手动计算梯度。为此,我们需要卷积核应用后得到的3x3矩阵。
如果我们取左上角的像素,它的值是 Gx = -2 和 Gy = 11。我们可以轻松计算出梯度幅度和方向:
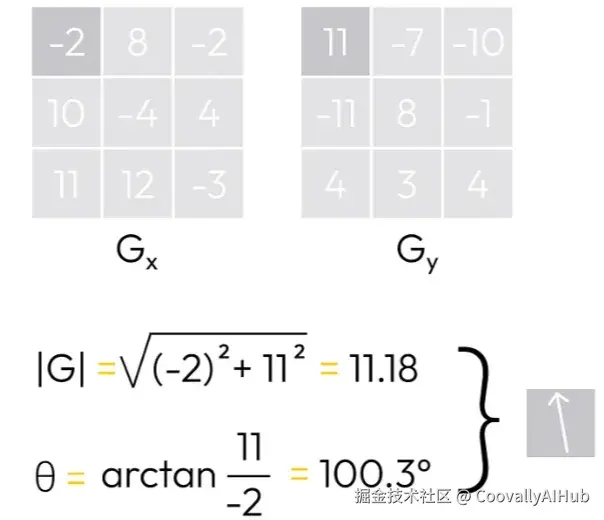
对于整个3x3矩阵,我们得到梯度的如下可视化:
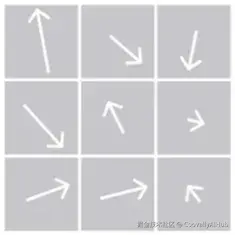
在实践中,建议在将核应用到矩阵之前对其进行归一化。为了示例的简洁,我们没有这样做。
Sobel算子
学习了图像导数和梯度的基础知识后,现在该来了解Sobel算子了,它用于近似计算导数和梯度。与之前尺寸为3x1和1x3的核相比,Sobel算子由一对3x3的核定义(分别用于两个轴):
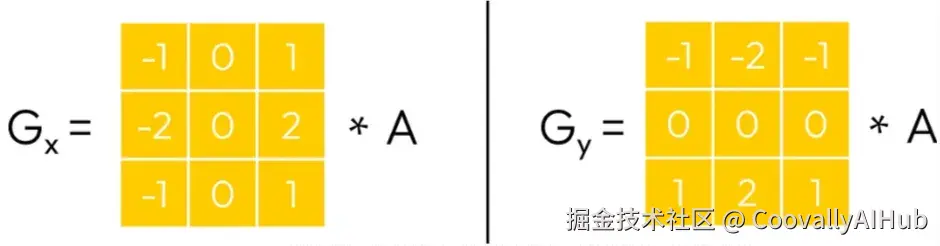
与之前只测量一维变化、忽略邻域中其他行和列的核相比,Sobel算子具有优势。它考虑了关于局部区域的更多信息。
另一个优势是Sobel对处理噪声更鲁棒。让我们看下面的图像块。如果我们计算中心红色元素(位于暗像素2和亮像素7边界上)周围的导数,我们应该得到5。问题在于存在一个值为10的噪声像素。

如果我们在红色元素附近应用水平1D核,它会过分关注像素值10,这显然是一个异常值。同时,Sobel算子则更稳健:它会考虑10,也会考虑它周围值为7的像素。从某种意义上说,Sobel算子应用了平滑。
在同时比较多个核时,建议对核矩阵进行归一化,以确保它们都在同一尺度上。
算子(包括Sobel)在图像分析中最常见的应用之一是特征检测。
对于Sobel和Scharr算子,它们通常用于检测边缘------即像素强度(及其梯度)发生剧烈变化的区域。
- 实践
要应用Sobel算子,使用cv2.Sobel函数就足够了。让我们看看它的参数:
ini
derivative_x = cv2.Sobel(image, cv2.CV_64F, 1, 0) # 计算x方向导数
derivative_y = cv2.Sobel(image, cv2.CV_64F, 0, 1) # 计算y方向导数- 第一个参数是输入的NumPy图像。
- 第二个参数 (cv2.CV_64F) 是输出图像的数据深度。问题在于,通常算子产生的输出图像可能包含超出0-255范围的值。这就是为什么我们需要指定希望输出图像拥有的像素类型。
- 第三和第四个参数分别代表x方向和y方向上的导数阶数。在我们的例子中,我们只需要x和y方向的一阶导数,所以我们传递值 (1, 0) 和 (0, 1)。
让我们看下面的例子,我们有一张数独输入图像:

让我们应用Sobel滤波器:
ini
import cv2
import matplotlib.pyplot as plt
image = cv2.imread("data/input/sudoku.png")
image = cv2.cvtColor(image, cv2.COLOR_BGR2GRAY)
# 使用Sobel算子
derivative_x = cv2.Sobel(image, cv2.CV_64F, 1, 0)
derivative_y = cv2.Sobel(image, cv2.CV_64F, 0, 1)
# 组合两个方向的导数
derivative_combined = cv2.addWeighted(derivative_x, 0.5, derivative_y, 0.5, 0)
# 查看值范围
min_value = min(derivative_x.min(), derivative_y.min(), derivative_combined.min())
max_value = max(derivative_x.max(), derivative_y.max(), derivative_combined.max())
print(f"值范围: ({min_value:.2f}, {max_value:.2f})")
# 可视化结果
fig, axes = plt.subplots(1, 3, figsize=(16, 6), constrained_layout=True)
axes[0].imshow(derivative_x, cmap='gray', vmin=min_value, vmax=max_value)
axes[0].set_title("水平导数")
axes[0].axis('off')
image_1 = axes[1].imshow(derivative_y, cmap='gray', vmin=min_value, vmax=max_value)
axes[1].set_title("垂直导数")
axes[1].axis('off')
image_2 = axes[2].imshow(derivative_combined, cmap='gray', vmin=min_value, vmax=max_value)
axes[2].set_title("组合导数")
axes[2].axis('off')
color_bar = fig.colorbar(image_2, ax=axes.ravel().tolist(), orientation='vertical', fraction=0.025, pad=0.04)
plt.savefig("data/output/sudoku_sobel.png")
plt.show()结果,我们可以看到水平和垂直导数能很好地检测到线条!此外,将这些线条组合起来使我们能够检测到两种类型的特征:

Scharr算子
Sobel算子的另一个流行替代品是Scharr算子:
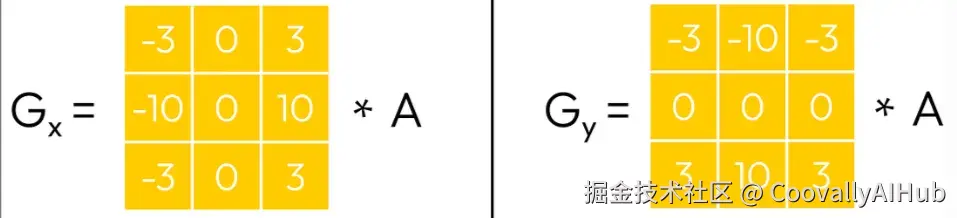
尽管其结构与Sobel算子非常相似,但Scharr核在边缘检测任务中实现了更高的精度。它具有一些关键的数学特性,本文中我们不打算探讨。
- 实践
使用Scharr滤波器与上面看到的Sobel滤波器非常相似。唯一的区别是方法名(其他参数相同):
ini
derivative_x = cv2.Scharr(image, cv2.CV_64F, 1, 0)
derivative_y = cv2.Scharr(image, cv2.CV_64F, 0, 1)这是我们使用Scharr滤波器得到的结果:

在这种情况下,很难注意到两种算子结果的差异。然而,通过查看颜色映射,我们可以看到Scharr算子产生的可能值范围(-800, +800)比Sobel的(-200, +200)大得多。这是正常的,因为Scharr核具有更大的常数。
这也是为什么我们需要使用特殊类型cv2.CV_64F的一个好例子。否则,值将被裁剪到标准的0到255范围,我们将丢失有关梯度的重要信息。
注意: 直接对cv2.CV_64F类型的图像应用保存方法会导致错误。要将此类图像保存到磁盘,需要将它们转换为另一种格式,并且只包含0到255之间的值。
结论
通过将微积分基础知识应用于计算机视觉,我们研究了图像的基本属性,这些属性使我们能够检测图像中的强度峰值。这些知识非常有用,因为特征检测是图像分析中的常见任务,特别是在图像处理有约束或者不使用机器学习算法的情况下。