Leetcode 51

1 题目

给定一个二叉搜索树的根节点 root ，和一个整数 k ，请你设计一个算法查找其中第 k小的元素（从 1 开始计数）。

示例 1：

复制代码

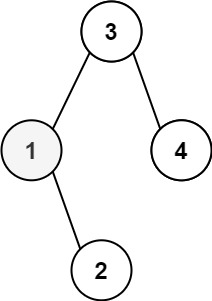
输入：root = [3,1,4,null,2], k = 1
输出：1

示例 2：

复制代码

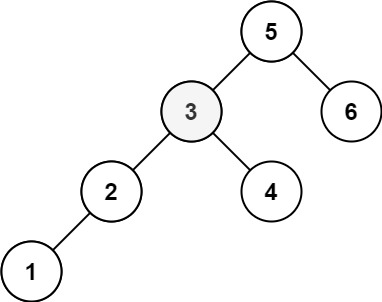
输入：root = [5,3,6,2,4,null,null,1], k = 3
输出：3

提示：

树中的节点数为 n 。
1 <= k <= n <= 104
0 <= Node.val <= 104

2 代码实现

cpp 复制代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
    private:
    int res = 0 ;
    int rank = 0 ;
    void traverse (TreeNode * root , int k ){
        if (root == nullptr){
            return;
        }

        traverse(root -> left , k);
        rank ++ ;
        
        if (k == rank){
            res = root -> val ;
            return ;
        }
        traverse(root -> right , k);
    }
public:
    int kthSmallest(TreeNode* root, int k) {
        traverse(root , k );
        return res;
    }
};

题解

这个解法是利用二叉搜索树（BST）的中序遍历特性来寻找第 k 小元素的递归实现，逻辑清晰且充分利用了 BST 的核心性质。下面从原理、代码细节和优缺点三个方面详细解释：

一、核心原理

BST 的关键性质是：中序遍历结果为升序序列（左子树 → 根节点 → 右子树）。因此，中序遍历过程中访问的第 k 个节点，就是整棵树中第 k 小的元素。

递归解法通过深度优先搜索（DFS）模拟中序遍历，在遍历过程中计数，当计数达到 k 时，当前节点的值即为答案。

二、代码细节拆解

1. 成员变量定义

cpp 复制代码

private:
int res = 0;   // 存储第 k 小的元素值
int rank = 0;  // 记录当前访问到的节点是第几个（计数用）

res：最终结果，找到第 k 小元素后赋值。
rank：遍历计数器，每访问一个节点（中序顺序）就 +1，直到等于 k。

2. 递归遍历函数 `traverse`

cpp 复制代码

void traverse(TreeNode* root, int k) {
    if (root == nullptr) {
        return;  // 空节点直接返回，终止递归
    }

    // 1. 先递归遍历左子树（中序遍历的"左"）
    traverse(root->left, k);

    // 2. 访问当前根节点（中序遍历的"根"）
    rank++;  // 每访问一个节点，计数 +1
    if (k == rank) {  // 当计数达到 k 时，找到目标
        res = root->val;  // 记录结果
        return;  // 提前返回，无需继续遍历
    }

    // 3. 再递归遍历右子树（中序遍历的"右"）
    traverse(root->right, k);
}

递归终止条件 ：遇到空节点（root == nullptr）时返回，避免无效递归。
中序遍历顺序 ：严格遵循 "左 → 根 → 右"：
- 先遍历左子树，确保左子树的所有节点（比当前根小）先被访问。
- 访问当前根节点时，计数器 rank 加 1，若等于 k，说明当前节点就是第 k 小元素，记录结果后直接返回（剪枝，减少无效遍历）。
- 最后遍历右子树（右子树的节点都比当前根大）。

3. 主函数 `kthSmallest`

cpp 复制代码

public:
int kthSmallest(TreeNode* root, int k) {
    traverse(root, k);  // 启动递归遍历
    return res;  // 返回找到的结果
}

调用递归函数 traverse 开始遍历，最终返回存储在 res 中的结果。

三、优缺点分析

优点：

逻辑简洁：直接利用 BST 中序遍历的升序性质，无需额外数据结构（如栈或数组），代码可读性高。
提前终止 ：当找到第 k 小元素后，通过 return 提前终止递归，避免遍历完整棵树（尤其是 k 较小时，效率很高）。
空间高效：空间复杂度为 O (h)（h 为树的高度），仅为递归栈的深度（平衡树 h=log n，最坏情况 h=n，即退化为链表）。

缺点：

递归栈限制：对于极端深的树（如 h=10^4），可能触发栈溢出（递归深度过深）。
成员变量依赖 ：使用了类的成员变量 res 和 rank 传递状态，若在多线程环境下需注意同步问题（但算法题中无需考虑）。

四、示例验证

以 root = [3,1,4,null,2]（BST 结构如下），k=3 为例：

bash 复制代码

中序遍历顺序为：1 → 2 → 3 → 4。
遍历过程：
- 左子树遍历：1 的左为空 → 访问 1（rank=1）→ 1 的右为 2 → 访问 2（rank=2）。
- 访问根节点 3（rank=3），此时 rank == k=3 → res=3，返回。
最终结果为 3，符合预期。

总结

该解法是 BST 第 k 小元素问题的经典递归实现，核心是通过中序遍历的升序特性，在遍历过程中计数并提前终止。适合理解递归思想和 BST 性质，实际工程中若担心栈溢出，可改用迭代版（用栈模拟中序遍历），但递归版的简洁性更适合算法题场景。

【冗余的想法：这题怎么做？我想中序遍历二叉搜索树，然后hash表映射，给出所要的k】

在 LeetCode 230 题 "二叉搜索树中第 K 小的元素" 中，你的思路（中序遍历 + 哈希表映射）是可行的，但可以进一步优化。

不过核心逻辑确实依赖 BST 中序遍历为升序的性质，下面详细说明实现步骤和优化点：

题目分析

目标：在 BST 中找到第 k 小的元素（k 从 1 开始计数）。
关键性质：BST 的中序遍历结果是严格升序的，因此第 k 个被访问的元素就是答案。

方法：中序遍历（无需哈希表，直接计数）

你的思路中**"哈希表映射" 其实是多余的**，因为中序遍历的顺序本身就是升序，只需在遍历过程中记录访问到的第 k 个元素即可，无需存储所有元素再映射。

步骤：

对 BST 进行中序遍历（左 → 根 → 右）。
遍历过程中维护一个计数器，每访问一个节点就将计数器 +1。
当计数器等于 k 时，当前节点的值就是第 k 小的元素，直接返回。

C 语言实现（迭代版，推荐）

迭代版使用栈模拟中序遍历，效率高且避免递归栈溢出风险：

cpp 复制代码

#include <stdlib.h>

// 二叉树节点定义
struct TreeNode {
    int val;
    struct TreeNode *left;
    struct TreeNode *right;
};

int kthSmallest(struct TreeNode* root, int k) {
    // 用数组模拟栈（存储节点指针），假设树高不超过 10000（题目约束范围内足够）
    struct TreeNode* stack[10000];
    int top = -1;  // 栈顶指针（-1 表示空栈）
    struct TreeNode* curr = root;
    int count = 0;  // 计数：当前访问到第几个元素

    while (top != -1 || curr != NULL) {
        // 左子树全部入栈（找到最左节点）
        while (curr != NULL) {
            stack[++top] = curr;  // 入栈
            curr = curr->left;
        }
        // 弹出栈顶元素（当前最小未访问元素）
        curr = stack[top--];
        count++;
        // 找到第 k 个元素，直接返回
        if (count == k) {
            return curr->val;
        }
        // 转向右子树
        curr = curr->right;
    }
    return -1;  // 理论上不会执行（k 合法）
}

C++ 实现（迭代版）

C++ 可使用 std::stack 简化栈操作，代码更简洁：

cpp 复制代码

#include <stack>

// 二叉树节点定义
struct TreeNode {
    int val;
    TreeNode *left;
    TreeNode *right;
    TreeNode() : val(0), left(nullptr), right(nullptr) {}
    TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
    TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};

class Solution {
public:
    int kthSmallest(TreeNode* root, int k) {
        std::stack<TreeNode*> stk;  // 栈存储节点指针
        TreeNode* curr = root;
        int count = 0;

        while (!stk.empty() || curr != nullptr) {
            // 左子树入栈
            while (curr != nullptr) {
                stk.push(curr);
                curr = curr->left;
            }
            // 弹出栈顶并计数
            curr = stk.top();
            stk.pop();
            count++;
            if (count == k) {
                return curr->val;
            }
            // 转向右子树
            curr = curr->right;
        }
        return -1;  // 冗余返回（k 合法时不会触发）
    }
};

为什么不需要哈希表？

中序遍历的顺序就是升序，第 1 个访问的是最小元素，第 2 个是次小元素，...，第 k 个就是目标。
用哈希表存储所有元素再取第 k-1 个（下标），虽然能得到结果，但会额外占用 O (n) 空间，且无需遍历完整棵树（找到后可提前退出），哈希表反而增加了不必要的开销。

时间复杂度

最优情况：O (h + k)，其中 h 是树的高度（栈的深度），当 k 较小时（如 k=1），只需遍历到最左节点即可。
最坏情况：O (n)（当 k=n 时，需遍历所有节点）。

空间复杂度：O (h)（递归栈或迭代栈的深度，平衡树 h=log n，最坏情况 h=n）。

这种方法充分利用了 BST 的中序遍历性质，是该题的最优解之一。

3 二叉搜索树（BST）的中序遍历结果为升序（推导）

在算法题中，二叉搜索树（BST）的中序遍历结果为升序是一个极其重要的性质，它是解决许多 BST 相关问题的核心突破口。

我们可以从 BST 的定义出发，严格推导这一性质，并理解其在解题中的应用价值。

一、从 BST 定义推导中序遍历的升序性

BST 的核心定义是：对任意节点，其左子树中所有节点的值 < 该节点的值，且右子树中所有节点的值 > 该节点的值 （注：若允许重复值，可能为<=或>=，但算法题中通常默认严格不等）。

结合中序遍历 "左子树 → 根节点 → 右子树" 的顺序，可递归证明中序遍历结果必然升序：

基础情况：空树或单节点树，中序遍历结果显然有序。
递归假设 ：对任意节点root，其左子树的中序遍历结果是升序，右子树的中序遍历结果也是升序。
递归推导 ：
- 左子树中所有节点的值 < root.val（由 BST 定义），因此左子树的中序遍历结果（升序）中，所有元素 < root.val。
- 右子树中所有节点的值 > root.val（由 BST 定义），因此右子树的中序遍历结果（升序）中，所有元素 > root.val。
- 中序遍历顺序为 "左子树结果 → root.val → 右子树结果"，拼接后整体必然是升序（例如：[1,2] → 3 → [4,5] 拼接为 [1,2,3,4,5]）。

因此，BST 的中序遍历结果一定是严格递增的序列。

二、这一性质的算法题应用场景

该性质将 BST 的结构特征与 "有序序列" 这一易于处理的数据形式关联起来，大幅简化问题。常见应用包括：

1. 验证 BST 合法性

问题：判断一棵二叉树是否为 BST。

常规思路：对每个节点，检查其值是否大于左子树最大值、小于右子树最小值（需递归传递范围，较繁琐）。

利用中序遍历：中序遍历该树，若结果是严格升序，则为 BST；否则不是。

优势：只需一次遍历，时间复杂度 O (n)，实现简单。

2. 寻找 BST 中的第 k 小元素（本题）

问题：在 BST 中找到第 k 小的节点值。

常规思路：遍历整棵树收集所有值，排序后取第 k 个（时间复杂度 O (n log n)，效率低）。

利用中序遍历：中序遍历是升序，第 k 个被访问的节点即为答案。可在遍历到第 k 个节点时直接返回，无需遍历完整棵树（最优时间 O (k)）。

3. 恢复被错误交换的 BST 节点

问题：BST 中两个节点被错误交换，导致结构破坏，找出这两个节点并恢复。

利用中序遍历 ：正常 BST 的中序遍历是升序，错误交换后会出现1~2 处 "降序对" （例如：正确序列[1,3,4,6,7]，交换 3 和 6 后变为[1,6,4,3,7]，降序对为 (6,4) 和 (4,3)）。

若有 1 处降序对：直接交换这两个节点。
若有 2 处降序对：交换第一对的前者和第二对的后者。

4. 构造 BST

问题：根据升序数组构造一棵平衡 BST（或任意 BST）。

利用中序遍历：升序数组是 BST 的中序遍历结果，因此可选择数组中间元素作为根，左半部分为左子树，右半部分为右子树（递归构造，天然平衡）。

三、总结

BST 的中序遍历升序性，本质是将 "树的结构约束" 转化为 "序列的有序性"。

在算法题中，这一性质允许我们用**处理有序序列的思路（如找第 k 小、检测逆序对、二分构造等）**解决 BST 问题，大幅降低思维复杂度和实现难度。

记住这一性质，能在解题时快速找到突破口。

1 题目

2 代码实现

题解

一、核心原理

二、代码细节拆解

1. 成员变量定义

2. 递归遍历函数 traverse

3. 主函数 kthSmallest

三、优缺点分析

优点：

缺点：

四、示例验证

总结

【冗余的想法：这题怎么做？我想中序遍历二叉搜索树，然后hash表映射，给出所要的k】

题目分析

方法：中序遍历（无需哈希表，直接计数）

步骤：

C 语言实现（迭代版，推荐）

C++ 实现（迭代版）

为什么不需要哈希表？

时间复杂度

3 二叉搜索树（BST）的中序遍历结果为升序（推导）

一、从 BST 定义推导中序遍历的升序性

二、这一性质的算法题应用场景

1. 验证 BST 合法性

2. 寻找 BST 中的第 k 小元素（本题）

3. 恢复被错误交换的 BST 节点

4. 构造 BST

三、总结

2. 递归遍历函数 `traverse`

3. 主函数 `kthSmallest`