文章目录
前言
嗨,我们又见面啦ヾ(≧∇≦*)ヾ,上一篇我们讲啦《数据结构二叉树之堆 ------ 优先队列与排序的高效实现(2)》,讲了堆的顺序结构的实现,今天我们来继续了解它的内容,继续分析堆

本篇涉及的知识点
前两部分:算法的时间复杂度和空间复杂度
第3部分:文件操作入门(上)------ 文件类型及顺序读写基础(含打开关闭)
文件操作入门(下)------ 随机读写、结尾判断、缓冲区及实战题目
一、向上调整法建堆和向下调整法建堆的时间复杂度计算
上一篇我们用了向上调整法和向下调整法进行操作,他们都可以进行建堆,但我们思考哪一种建堆更好?现在我们来分析他们的时间复杂度来观察他们的区别
1、向上调整法建堆的时间复杂度
设N个节点,高度为h,根据二叉树特点,h=log(N+1)
下图为算时间复杂度过程
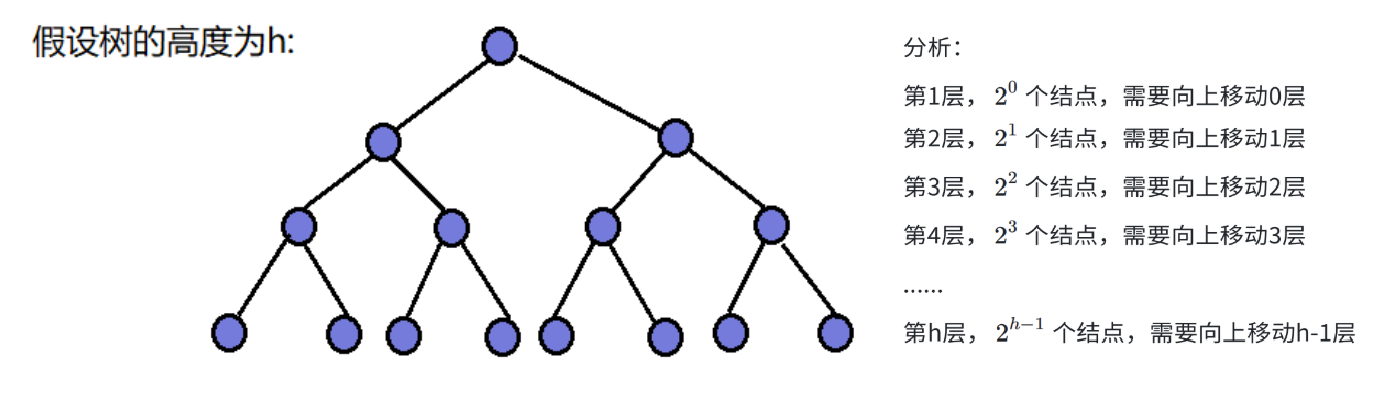
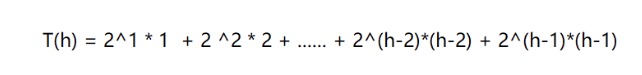
再用错位相减法和h=log(N+1)

我们可以算出向上调整法时间复杂度为O(N*logN)
2、向下调整法建堆的时间复杂度
二者的计算方式十分相近,过程如下图
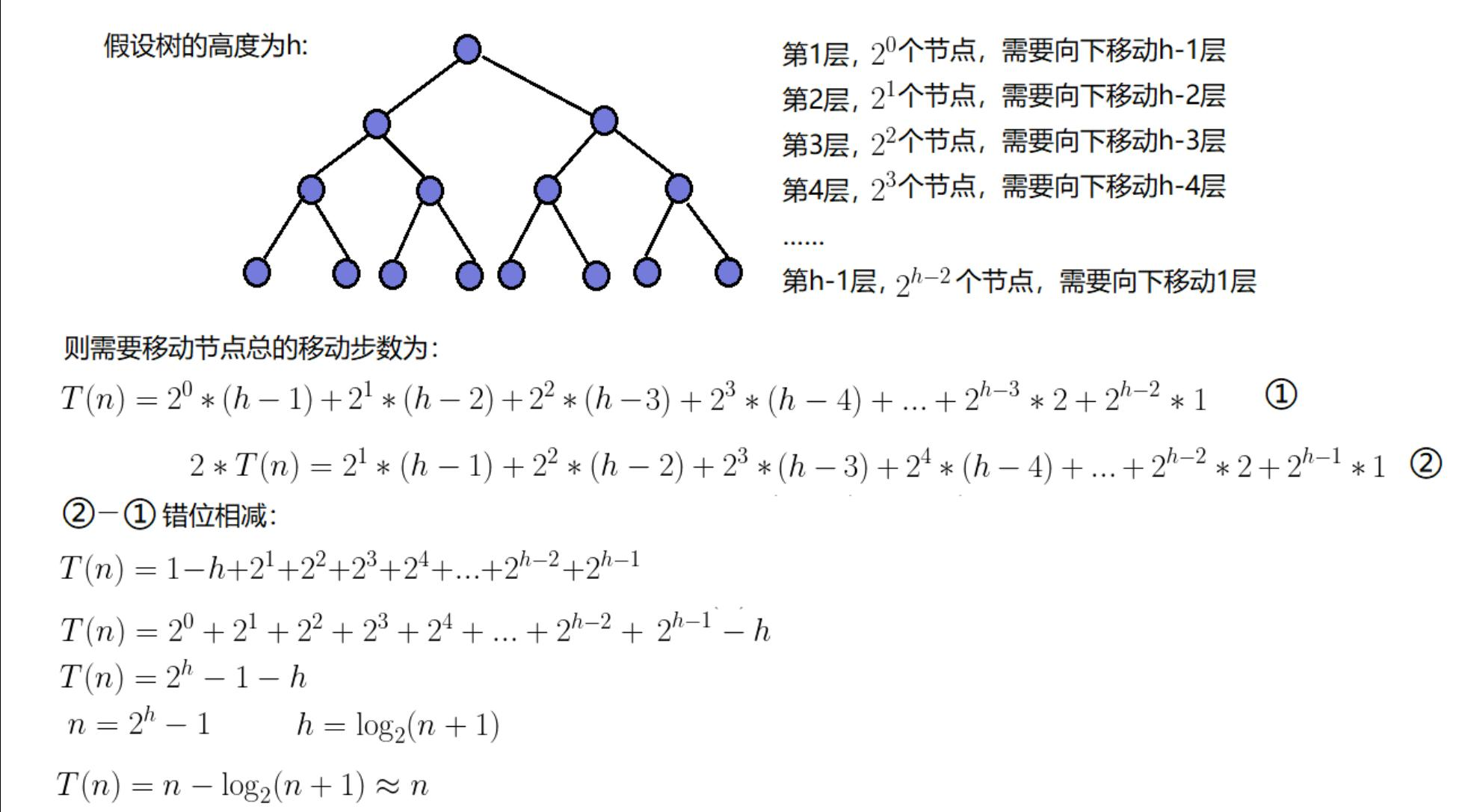
经计算向下调整法的时间复杂度为O(N)
3、总结
向上调整法建堆和向下调整法建堆看似一样,但实际却不一样,向下调整法更优,这是为什么呢?我们在计算中应该发现了
向下调整法:节点数量多的层调整次数少,节点数量少的层调整次数多
向上调整法:节点数量多的层调整次数多,节点数量少的层调整次数少
这就导致了向下调整法的更优
二、堆排序的时间复杂度
接下来我们来计算一下堆排序的时间复杂度,我们上一篇最后已经讲了数组空间复杂度为O(1)的方法,那个就是真正的堆排序,我们回顾一下,就是最后一个与堆头互换,元素个数size--,再进行向下调整法,反复操作,最终排序完成
堆排序时间复杂度计算过程
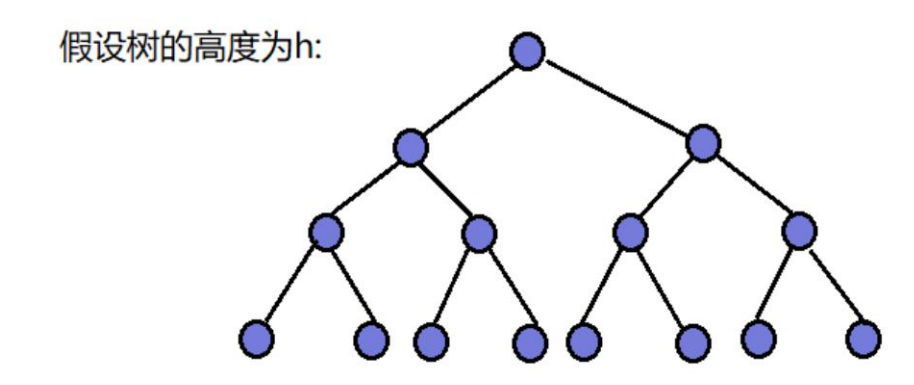
进行堆排序时,倒着看
最后1层节点与堆头交换之后,最多向下移动h-1层
倒数第2层节点与堆头交换之后,最多向下移动h-2层(因为到这一层时,元素个数size已经减到倒数第2层了,所以最多向下移动h-2层)
倒数第3层节点与堆头交换之后,最多向下移动h-3层
......
第2层节点与堆头交换之后,最多向下移动1层
第1层,最多向下0层
我们发现这个过程与向上调整法计算一样,只是多了一个交换过程,所以操作次数为
n+n*logn,用大O表示法,时间复杂度为O(n*logn)
不了解时间复杂度的可以看算法的时间复杂度和空间复杂度
三、TOP-K问题
TOPK问题:即求数据集合中前K个最大的元素或者最小的元素,一般情况下数据量比较大
比如:专业前10名、世界500强、富豪榜、游戏中前100的活跃玩家等
对于TOP-K问题,能想到的最简单直接的方式就是排序,但是:
如果数据量非常大,排序就不太可取了(可能数据都不能一下子全部加载到内存中)。
最佳的方式就是用堆来解决,基本思路如下:
- 用数据集合中前K个元素来建堆。
前k个最大的元素,则建小堆。
前k个最小的元素,则建大堆 - 用剩余的N-K个元素依次与堆顶元素来比较,不满足则替换堆顶元素
将剩余N-K个元素依次与堆顶元素比完之后,堆中剩余的K个元素就是所求的前K个最小或者最大的元素。
问题及思考过程
如果面试官这样问你10亿个数中怎么找到最大的前10个
我们可能会想到直接建小堆进行排序,但我们先算出10亿需要的内存
1G = 1024MB = 1024 * 1024KB = 1024 * 1024 * 1024byte10亿=4亿字节,相当于3点多G,太占内存了,但还可以操作
这时面试官说只有1G内存
这时我们可以分4个堆进行,分别找出每个堆的前10个大的再比较
这时面试官又改为只有1KB内存
这时我们有点蒙,怎么做呢,哦~
这时我们就想到了一个完美的方法------建立一个10个数的小堆,把10个数放进去,再用剩下的数和堆顶元素比较,比堆顶元素大,交换,再进行向下调整法,最后剩下的10个就是最大的10个啦

所以我们可以总结
找最大的前K个数据,建小堆,遍历剩下的数据和堆顶比,比堆顶要大的就和堆顶交换;
找最小的前K个数据,建大堆,遍历剩下的数据和堆顶比,比堆顶要小就和堆顶交换。
实现
由于10个亿数据太多了,我们改为10万进行操作(能快速了解方法)
1、造数据
先造10万个数据进行解决问题前的操作,用rand()进行造数据
造数据
c
#include"Heap.h"
#include<time.h>
void CreateNDate()
{
// 造数据
int n = 100000;
srand(time(0));
const char* file = "data.txt";
FILE* fin = fopen(file, "w");
if (fin == NULL)
{
perror("fopen error");
return;
}
for (int i = 0; i < n; ++i)
{
int x = (rand() + i) % 10000000;//加i是为了减少重复
fprintf(fin, "%d\n", x);
}
fclose(fin);
}
int main()
{
CreateNDate();
return 0;
}2、进行建k个节点的堆解决问题
我们按照前面思路进行读取,解决问题
代码如下:
c
#include"Heap.h"
void TestHeap3()
{
int k;
printf("请输入k>:");
scanf("%d", &k);
int* kminheap = (int*)malloc(sizeof(int) * k);
if (kminheap == NULL)
{
perror("malloc fail");
return;
}
const char* file = "data.txt";
FILE* fout = fopen(file, "r");
if (fout == NULL)
{
perror("fopen error");
return;
}
// 读取文件中前k个数
for (int i = 0; i < k; i++)
{
fscanf(fout, "%d", &kminheap[i]);
}
// 建K个数的小堆
for (int i = (k - 1 - 1) / 2; i >= 0; i--)
{
AdjustDown(kminheap, k, i);
}
// 读取剩下的N-K个数
int x = 0;
while (fscanf(fout, "%d", &x) > 0)
{
if (x > kminheap[0])
{
kminheap[0] = x;
AdjustDown(kminheap, k, 0);
}
}
printf("最大前%d个数:", k);
for (int i = 0; i < k; i++)
{
printf("%d ", kminheap[i]);
}
printf("\n");
}
int main()
{
/*CreateNDate();*/
TestHeap3();
return 0;
}结果

可我们不知道这对不对,总不能一个一个对吧,这时就要用到了%,可能大家不知道我在造数据时为什么%10000000,就是控制造数据的范围,造完数据后,我在手动改几个数据让他们超过1000万,再观察就知道代码准确性啦
造完数据改数据,下图是其中改的一些,总共10个改为超过1000万
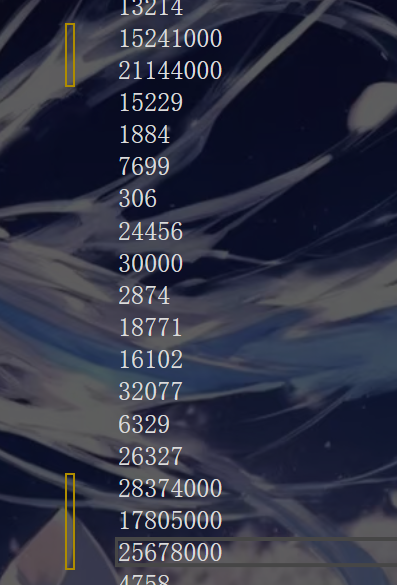
这时再验证

我们发现他们都超过1000万,证明代码正确实现
四、结尾语
嗨φ(>ω<) ,本篇到这里就结束啦,我们对堆的学习也到这里就结束啦,本篇相关知识链接已经放在开头啦,本篇主要比较向下调整法和向上调整法的时间复杂度和堆排序的时间复杂度以及TOP-K问题,相信大家都有所收获,欢迎大家来评论区提供建议和补充,下一篇我们就要讲二叉树的链式结构的实现,敬请期待吧(其实我也挺期待与大家见面☆(≧∀≦ )ノ )!

前两篇
《数据结构二叉树之堆 ------ 优先队列与排序的高效实现(2)》
数据结构之初识二叉树(1)------核心概念入门
感谢大家的支持啦,博主会继续努力哒!