文章目录
(用二分算法的契机:在暴力解法中发现解集有二段性)
⼆分算法的原理以及模板其实是很简单的,主要的难点在于问题中的各种各样的细节问题。因此,⼤多数情况下,只是背会⼆分模板并不能解决题⽬,还要去处理各种乱七⼋糟的边界问题。
(自己创造一些极端例子可以很好的解决一些边界问题,比如目标值是2,可以创造一组全是2的序列、一组全部小于2的序列,一组全部大于2的序列或者0、3这样的既有大于目标值也有小于目标值但是没有等于目标值的序列)
模板题:在排序数组中查找元素
根据题目讲解算法原理
题目描述

题目解析
因为本题数组是不递减的,所以具有二段性,在序列中选中某个值后在该值的左边的元素一定小于等于该值,在该值的右边的元素一定大于等于该值。
本题可以拆解成两个子问题:查找区间起始位置和查找区间终止位置。
查找起始位置:
本题根据题意把序列划分为两部分,划分依据是一部分包含目标,一部分不包含目标,左边部分是小于target(区间中不包含目标),右边部分是大于等于target(区间中包含目标),每次计算出中间结点mid后都要判断mid位于左半部分还是右半部分。
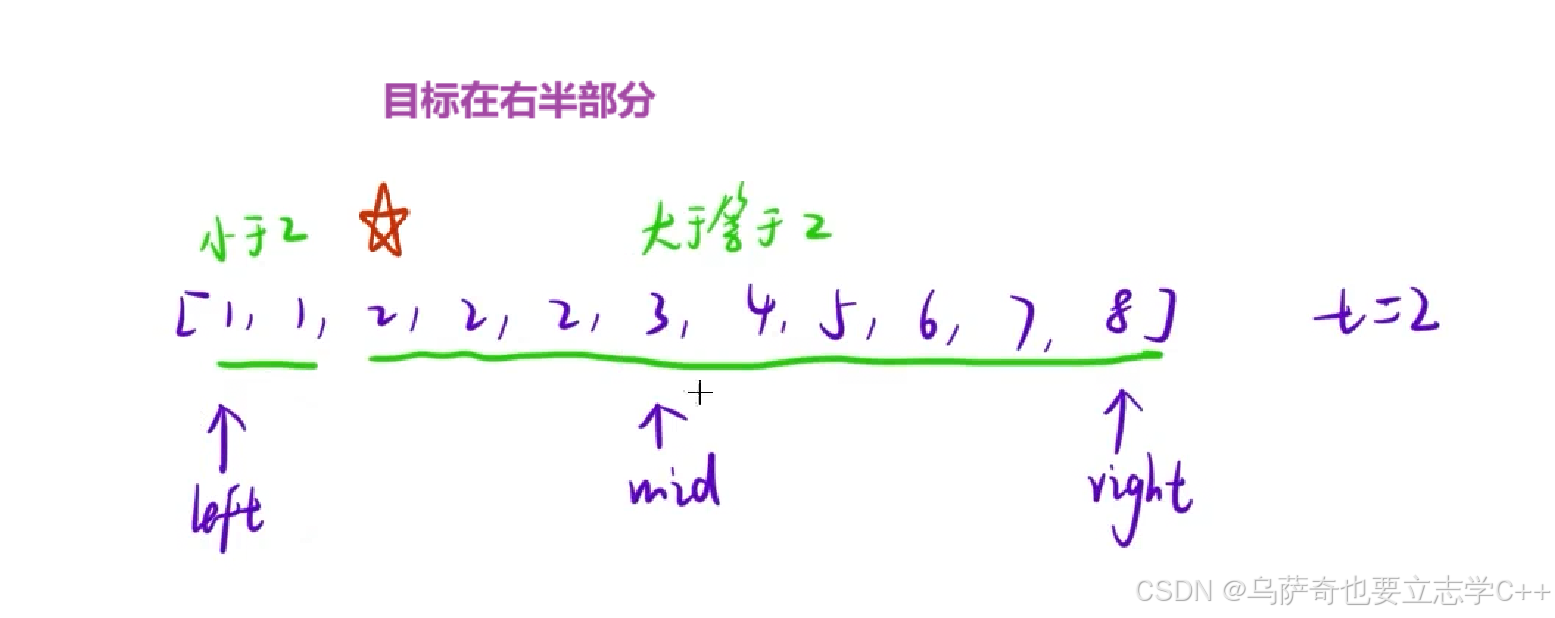
任何二分查找逻辑都要讨论下面三种细节:
1、求中点的方式:
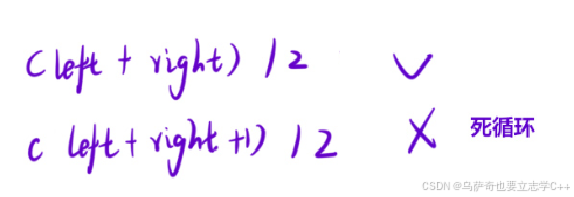
left+right后加1或者不加1的区别是当区间个数是偶数个时去靠右那个还是靠左那个,不加1取靠右,加1取靠左,但当区间个数是奇数个时都是取同一个元素。
我们知道目标在右半部分,所以当序列为偶数个时如果取靠右哪个区间中点,当mid为靠右哪个区间中点时,接下来的逻辑是right = mid,这时无论while循环条件是 left < right 还是 left <= right 都会一直死循环,因为left和right永远不会重合。
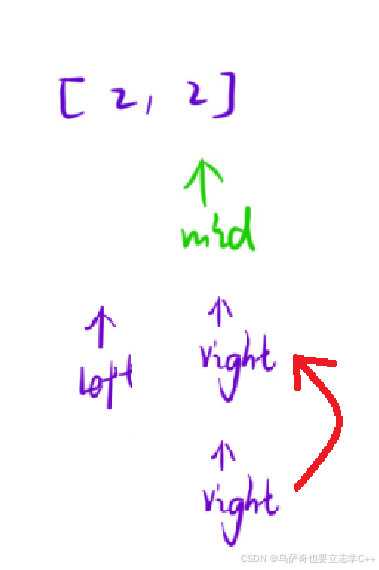
但是当我们取靠左哪个区间中点时接下来的逻辑是
left = mid + 1,这时left和right就成功重合了,达到了循环退出的条件,所以重合后就需要退出循环了。
2、while循环条件:
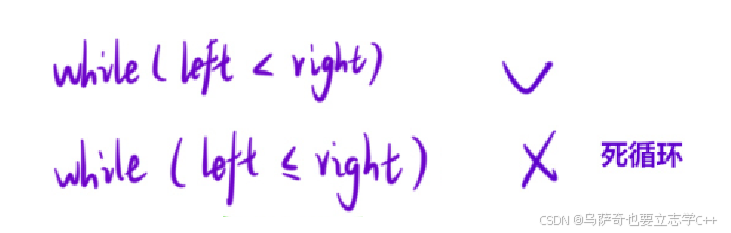
根据我们前面对求中点方式的讨论,我们知道循环退出条件必须是left < right,否则会出现死循环。
3、二分结束后,相遇点的情况:二分循环结束后正常情况下相遇点就是最终结果,但是不排除有例外情况比如整个区间中根本没有目标元素,例如(0、0、3、3),所以需要判断一下相遇点是否是我们想要的结果。
查找终止位置:
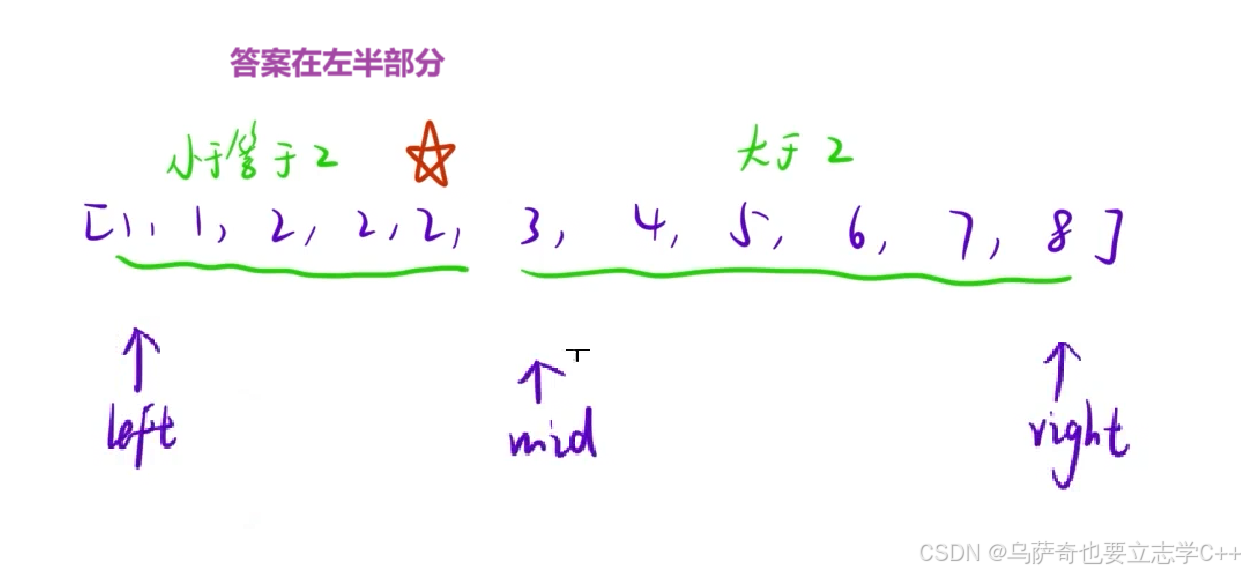
1、求中点的方式:
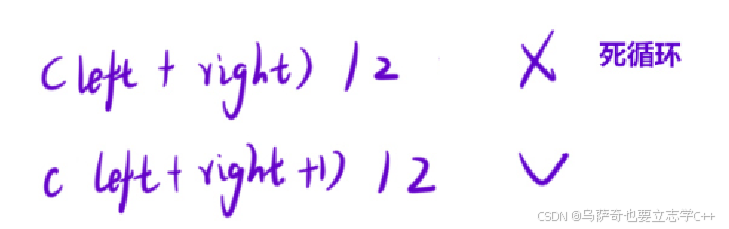
因为这里目标在左半部分,所以当区间为偶数个时中间结点要取靠右哪个。
2、while循环条件:
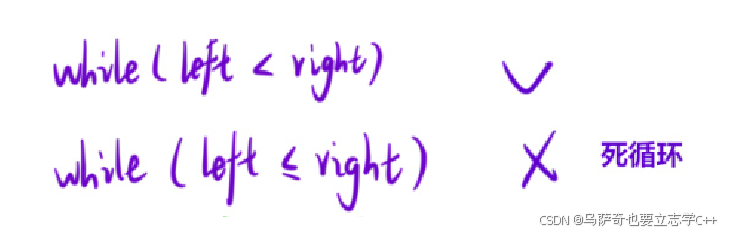
和求起始位置一样,这里也是左右结点重合后即退出,否则会出现死循环。
代码
cpp
int findrleft(vector<int>& v, int target)
{
int size = v.size();
int left = 0, right = size - 1, mid = 0;
while (left < right)
{
mid = (left + right) / 2;
if (v[mid] < target)
{
left = mid + 1;
}
else
{
right = mid;
}
}
//出循环
int ret = left;
if (v[ret] == target)
return ret;
else
return -1;
}
int findrright(vector<int>& v, int target)
{
int size = v.size();
int left = 0, right = size - 1, mid = 0;
while (left < right)
{
mid = (left + right + 1) / 2;
if (v[mid] <= target)
{
left = mid;
}
else
{
right = mid - 1;
}
}
//出循环
int ret = left;
if (v[ret] == target)
return ret;
else
return -1;
}
class Solution {
public:
vector<int> searchRange(vector<int>& nums, int target) {
if(nums.size() == 0)
{
return {-1, -1};
}
else{
int rleft = findrleft(nums, target);
int rright = findrright(nums, target);
return {rleft, rright};
}
}
};提炼模板

- 上面两个模板代码是配套使用的,不⽤死记硬背,算法原理搞清楚之后,在分析题⽬的时候⾃然⽽然就知道要怎么写⼆分的代码,小编再啰嗦一点,if/else中的判断条件是mid落在两个区间(目标值可能所在区间和不存在目标值区间)的哪个区间。
- 仅需记住⼀点, if/else 中出现 −1 的时候
(如 else r = mid - 1),求mid时需要 +1 就够了。- 为了防⽌求mid时 l + r 结果溢出,可以用下⾯的⽅式: mid = l + (r - l) / 2 或 mid = l + (r - l + 1) / 2
4、差分适用于找边界、计数、找最近值
库函数中的⼆分查找
lower_bound和upper_bound是库函数中实现二分查找的两个函数接口,它们在< algorithm >头文件中。
- lower_bound :⼤于等于 x 的最⼩元素,返回的是迭代器;时间复杂度: O(log N) 。
- upper_bound :⼤于 x 的最⼩元素,返回的是迭代器。时间复杂度: O(log N) 。
- 它们都要传三个参数,第一个参数传待查找区间首元素的迭代器,第二个参数传待查找区间尾元素的下一个元素的迭代器,第三个参数传带查找元素数值。
⼆者均采⽤⼆分实现。但是 STL 中的⼆分查找只能适⽤于"在有序的数组中查找",如果是⼆分答案就不能使⽤。因此还是需要记忆⼆分模板。
练习题
牛可乐和魔法封印
题目描述
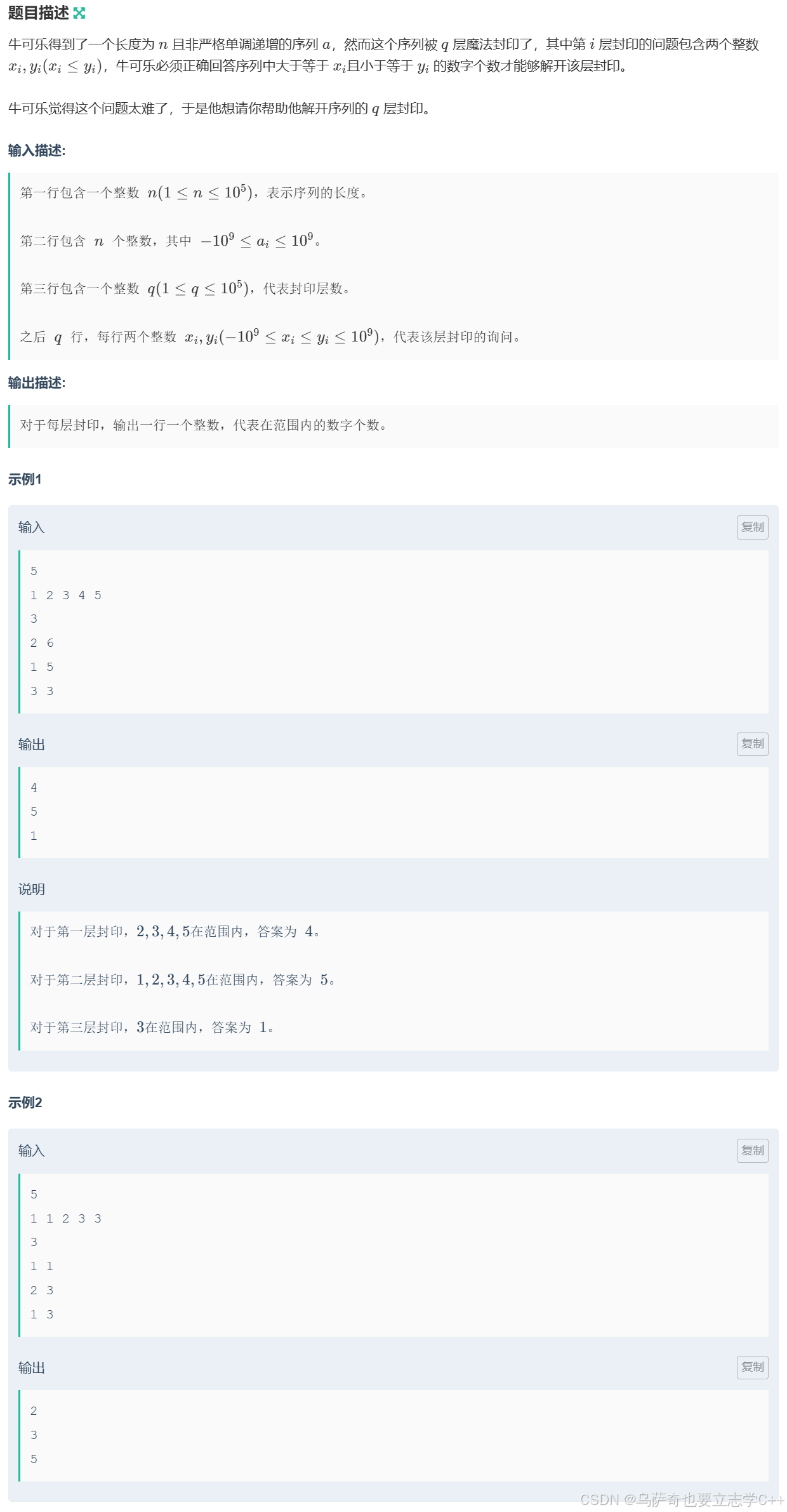
题目解析
没写出正确答案原因:
没有考虑输入为0,也就是区间不存在的情况,如(2,3)里找4-5。
本题依旧是二分模板题,注意考虑二分结束后区间是否合法。
代码
cpp
#include <iostream>
using namespace std;
const int M = 1e5 + 10;
int a[M];
int n; //序列长度
int binary_search(int x, int y)
{
//找有效区间左端点
int l = 1, r = n;
while (l < r)
{
int mid = (l + r) / 2;
if (a[mid] < x)
{
l = mid + 1;
}
else
{
r = mid;
}
}
//若区间最大值都比x小,故没有有效区间,例如(2,3)里找4-5,l最后为3下标
if(a[l] < x) return 0;
int left = l;
//找有效区间右端点
l = 1, r = n;
while (l < r)
{
int mid = (l + r + 1) / 2;
if (a[mid] <= y)
{
l = mid;
}
else
{
r = mid - 1;
}
}
//区间最大值都比y小,故没有有效区间。例如(4,5)里找2-3,l最后为2下标
if(a[l] > y) return 0;
int right = l;
return (right - left + 1);
}
int main()
{
cin >> n;
for (int i = 1; i <= n; i++)
{
cin >> a[i];
}
int q; cin >> q;
int x, y;
while (q--)
{
cin >> x >> y;
cout << binary_search(x, y) << endl;
}
return 0;
}A-B数对
题目描述
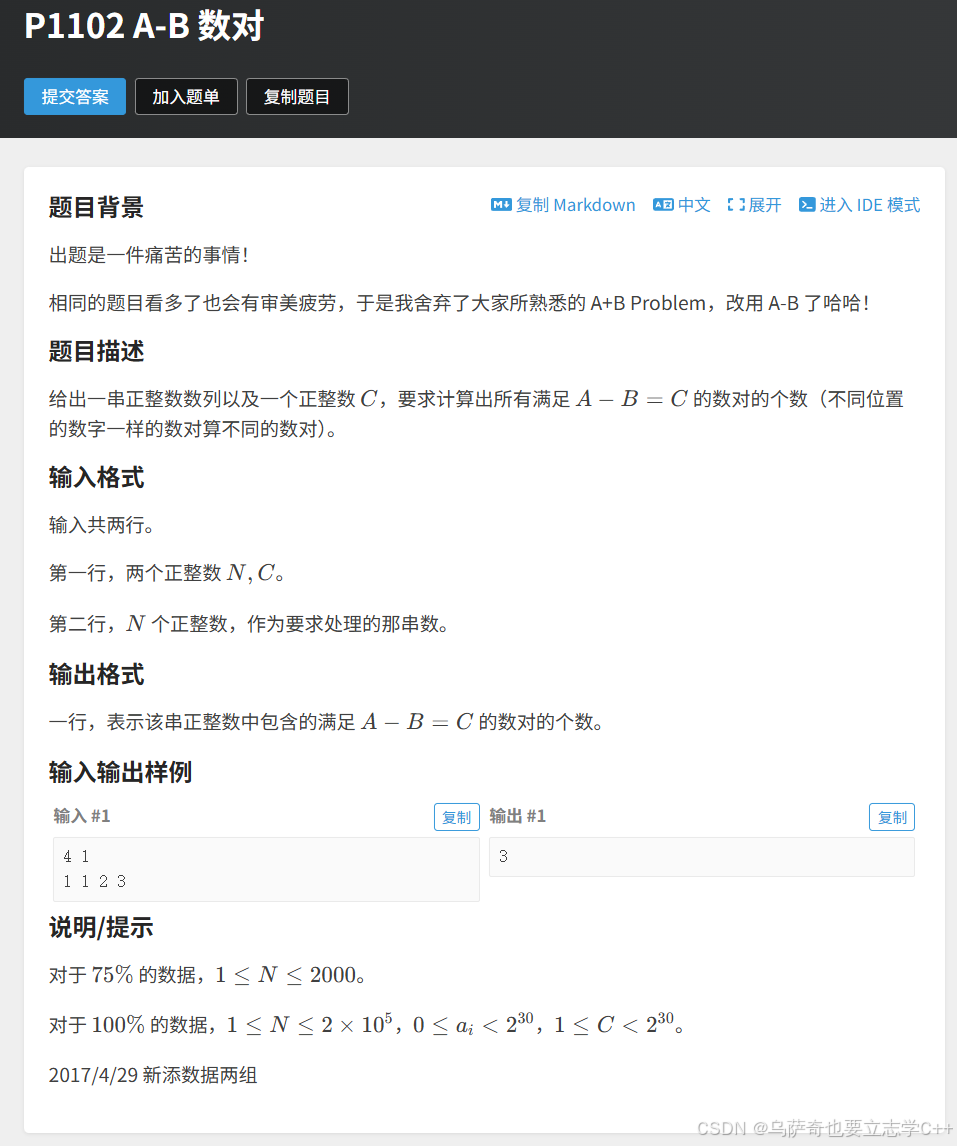
题目解析
本题我们在介绍哈希表的时候见过,本题的最优解仍是利用哈希表,把它放在这里在讲一遍是小编想给大家介绍一种思考问题的方法:把无序序列排成有序后说不定有新的思路。
因为本题的序列是无序的,所以我们可以把它拍成有序,排成有序后遍历整个有序数组,把遍历到的元素当作b,然后找b对应的a个数(a = b + c),找a的个数就相当于找a区间的长度,因为序列有序,所以可以用二分查找a区间的长度。
注意:本题ret可能溢出,用long long存储。
代码
cpp
#include <iostream>
#include <algorithm>
using namespace std;
typedef long long LL;
const int M = 2e5 + 10;
int t[M];
int main()
{
int n, c;
cin >> n >> c;
//输出数据
for (int i = 1; i <= n; i++)
{
cin >> t[i];
}
//将原数组排序
sort(&t[1], &t[n + 1]);
//遍历原数组,把遍历到的元素当作b,找b对应的a个数(a = b + c)
LL ret = 0;
for (int i = 1; i <= n; i++)
{
int a = t[i] + c;
auto left = lower_bound(&t[i], &t[n + 1], a); //遍历t[i]后面的区间
auto right = upper_bound(&t[i], &t[n + 1], a);
//right - left后不用加1,因为left本身指向有效区间末尾元素的下一个元素
ret += (right - left); //迭代器差值等于元素个数
}
cout << ret << endl;
return 0;
}烦恼的高考志愿
题目描述
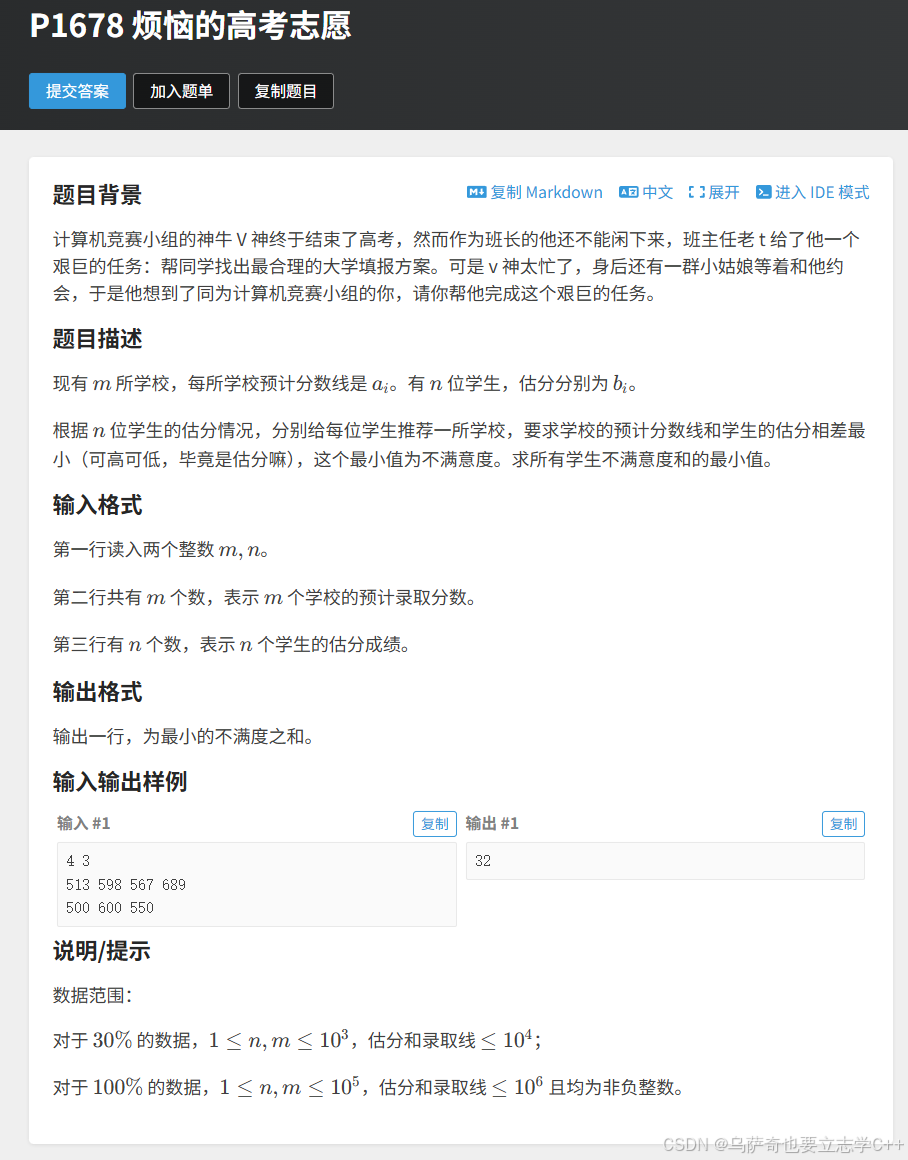
题目解析
没写出正确答案原因及原始代码:
思路错误,想的是找right - left = 1也就是差值为1时进行判断,正确思路应该是找到大于等于给定分数b的最小值,然后进行判断。
cpp
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1e5 + 10;
int a[N]; //学生分数
int main()
{
int m, n;
cin >> m >> n;
//初始化数据
for (int i = 1; i <= m; i++)
{
cin >> a[i];
}
//给原始数组排序
sort(&a[1], &a[m]);
// 查分
int s = 0, ret = 0; //单个分数,返回值
while(n--)
{
cin >> s;
int left = 1, right = m;
int flag = 1; //默认院校分数数组中有与学生分数相同的院校或学生分数在区间之外
while (left < right)
{
if (right - left == 1 && s > a[left] && s < a[right])
{
//数组中无与学生分数相同的院校,查找距离最近的值
int tmp = (s - a[left]) < (a[right] - s) ? (s - a[left]) : (a[right] - s);
ret += tmp;
flag = 0;
break;
}
int mid = (left + right) / 2;
if (a[mid] < s)
{
left = mid + 1;
}
else
{
right = mid;
}
}
//查找到了与学生分数相同的院校或学生分数在区间之外,取区间端点
if(flag)
ret += abs(a[left] - s);
}
cout << ret;
return 0;
}本题有两个解题思路,本质就是给定一个数b,在数组中找到离数b最近的元素。
一、首先可以利用set存储所有学校的录取分数线,然后遍历所有学生分数并用lower_bound找到大于等于特定学生分数b的最小值的下标,将该下标减一就得到了小于等于b的最大值,然后比较这两个值哪个离b最近,并把差值加到ret中。
二、利用差分模板,同样需要首先找到大于等于特定学生分数b的最小值的下标,后面的流程和法一相同。
代码
cpp
//法一:利用set
#include <iostream>
#include <set>
#include <algorithm>
using namespace std;
typedef long long LL;
const int INF = 1e7 + 10;
set<int> a; //学生分数
int main()
{
int m, n;
cin >> m >> n;
//初始化数据
for (int i = 1; i <= m; i++)
{
int t;
cin >> t;
a.insert(t);
}
// 插入左右护法,防止迭代器越界
a.insert(INF);
a.insert(-INF);
// 差分
int s = 0; //单个分数
LL ret = 0; //返回值
while (n--)
{
cin >> s;
auto rit = a.lower_bound(s); //rit指向大于等于s的最小值
int r = *rit;
auto lit = --rit; //lit指向(*rit)左边的元素
int l = *lit;
//int tmp = ((*rit) - s) < (s - (*lit)) ? ((*rit) - s) : (s - (*lit));
int tmp = min(r - s, s - l);
ret += tmp;
}
cout << ret;
return 0;
}
//法二:利用差分模板
#include <iostream>
#include <algorithm> //让min可用
#include <cmath> //让abs可用
using namespace std;
typedef long long LL;
const int N = 1e5 + 10;
LL a[N]; //学生分数
int main()
{
int m, n;
cin >> m >> n;
//初始化数据
for (int i = 1; i <= m; i++)
{
cin >> a[i];
}
//给原始数组排序
sort(&a[1], &a[m + 1]);
//添加左护法,防止迭代器越界
a[0] = -1e7 + 10;
// 差分求数组a中大于等于s的最小值
LL s = 0, ret = 0; //单个分数,返回值
while (n--)
{
cin >> s;
int left = 1, right = m;
while (left < right)
{
int mid = (left + right) / 2;
if (a[mid] < s)
{
left = mid + 1;
}
else
{
right = mid;
}
}
int r = a[left]; //大于等于s的最小值
int l = a[left - 1]; //小于等于s的最大值
int tmp = min(abs(r - s), abs(l - s));
ret += tmp;
}
cout << ret;
return 0;
}以上就是小编分享的全部内容了,如果觉得不错还请留下免费的关注和收藏如果有建议欢迎通过评论区或私信留言,感谢您的大力支持。
一键三连好运连连哦~~
