算法基础篇：（十九）吃透 BFS！从原理到实战，解锁宽度优先搜索的核心玩法

_OP_CHEN2025-11-29 12:55

目录

前言

[一、BFS 到底是什么？------ 从 "一层一层找答案" 说起](#一、BFS 到底是什么？—— 从 “一层一层找答案” 说起)

[1.1 BFS 的核心思想](#1.1 BFS 的核心思想)

[1.2 BFS 的基本框架](#1.2 BFS 的基本框架)

[二、BFS 经典例题实战 ------ 从基础到进阶](#二、BFS 经典例题实战 —— 从基础到进阶)

[2.1 基础款：马的遍历（洛谷 P1443）](#2.1 基础款：马的遍历（洛谷 P1443）)

题目描述

核心分析

完整代码

关键细节

[2.2 进阶款：kotori 和迷宫（牛客网）](#2.2 进阶款：kotori 和迷宫（牛客网）)

题目描述

核心分析

完整代码

关键细节

[2.3 优化款：Catch That Cow（洛谷 USACO07OPEN）](#2.3 优化款：Catch That Cow（洛谷 USACO07OPEN）)

题目描述

核心分析

完整代码

关键细节

[2.4 高阶款：八数码难题（洛谷 P1379）](#2.4 高阶款：八数码难题（洛谷 P1379）)

题目描述

核心分析

完整代码

关键细节

[三、BFS 的扩展玩法 ------ 多源 BFS、01 BFS](#三、BFS 的扩展玩法 —— 多源 BFS、01 BFS)

[3.1 多源 BFS：矩阵距离（牛客网）](#3.1 多源 BFS：矩阵距离（牛客网）)

核心思想

典型场景

核心代码片段

[3.2 01 BFS：小明的游戏（洛谷 P4554）](#3.2 01 BFS：小明的游戏（洛谷 P4554）)

核心思想

典型场景

核心代码片段

[四、BFS 的避坑指南 ------ 这些错误 90% 的人都会犯](#四、BFS 的避坑指南 —— 这些错误 90% 的人都会犯)

总结

前言

在算法的世界里，搜索类算法是解决 "找路径、求最优" 问题的核心武器，而宽度优先搜索（BFS）更是其中的 "明星选手"------ 它凭借 "逐层扩展、最短路径" 的特性，成为处理边权为 1 的最短路问题的首选。今天，我们就从零开始，把 BFS 的底层逻辑、实现技巧、经典例题掰开揉碎讲清楚，让你不仅会写代码，更能理解 "为什么要这么写"。下面就让我们正式开始吧！

一、BFS 到底是什么？------ 从 "一层一层找答案" 说起

1.1 BFS 的核心思想

BFS（Breadth-First Search），直译是 "宽度优先搜索"，也常被称作 "广度优先搜索"。如果说深度优先搜索（DFS）是 "一条路走到黑，走不通再回头"，那 BFS 就是 "稳扎稳打，一层一层往外扩"。

想象一个场景：你站在迷宫的起点，想要找到出口，且要求走最少的步数。DFS 的做法是随便选一个方向冲到底，碰壁了就退回来换方向；而 BFS 的做法是，先把起点周围一步能到的位置都走一遍，再把这些位置周围两步能到的位置走一遍...... 直到找到出口。这种 "逐层探索" 的方式，天然保证了 "第一次遇到目标时，走的步数就是最少的"------ 这也是 BFS 最核心的优势：在边权为 1 的图 / 网格中，能直接求出起点到目标点的最短路径。

1.2 BFS 的基本框架

BFS 的实现离不开两个关键工具：队列 （用来存储待扩展的节点）和标记数组（用来记录节点是否被访问过，避免重复搜索）。

我们先给出 BFS 的通用模板（以网格类问题为例），后续所有例题都会基于这个模板变形：

cpp 复制代码 
#include <iostream>
#include <queue>
#include <cstring>
using namespace std;

// 定义方向数组（上下左右）
int dx[] = {0, 0, 1, -1};
int dy[] = {1, -1, 0, 0};
// 标记数组：记录是否访问过，也可记录最短距离
int dist[100][100];
// 网格大小
int n, m;

void bfs(int start_x, int start_y) {
    // 初始化：距离数组置为-1（表示未访问）
    memset(dist, -1, sizeof dist);
    // 队列存储坐标对
    queue<pair<int, int>> q;
    // 起点入队，距离置为0
    q.push({start_x, start_y});
    dist[start_x][start_y] = 0;

    // 队列不为空时循环
    while (!q.empty()) {
        // 取出队头节点
        auto t = q.front();
        q.pop();
        int x = t.first, y = t.second;

        // 扩展四个方向
        for (int i = 0; i < 4; i++) {
            int nx = x + dx[i];
            int ny = y + dy[i];
            // 检查边界 + 未访问
            if (nx >= 1 && nx <= n && ny >= 1 && ny <= m && dist[nx][ny] == -1) {
                // 更新距离：当前距离+1
                dist[nx][ny] = dist[x][y] + 1;
                // 新节点入队
                q.push({nx, ny});
                // 找到目标可提前退出（可选）
                if (nx == 目标x && ny == 目标y) return;
            }
        }
    }
}

这个模板看似简单，但藏着几个关键细节：

  1. 队列的作用 ：保证 "先进先出"，符合 BFS "逐层扩展" 的逻辑；
  2. 距离数组 dist：既标记是否访问，又记录最短距离，一举两得；
  3. 方向数组：把 "上下左右" 的移动转化为循环，简化代码；
  4. 提前退出：如果目标明确，找到后可直接 return，减少不必要的计算。

二、BFS 经典例题实战 ------ 从基础到进阶

光说不练假把式，接下来我们结合 4 道经典例题，一步步拆解 BFS 的应用技巧，从 "马的遍历" 到 "八数码难题"，难度由浅入深，带你吃透 BFS 的精髓。

2.1 基础款：马的遍历（洛谷 P1443）

题目链接： https://www.luogu.com.cn/problem/P1443

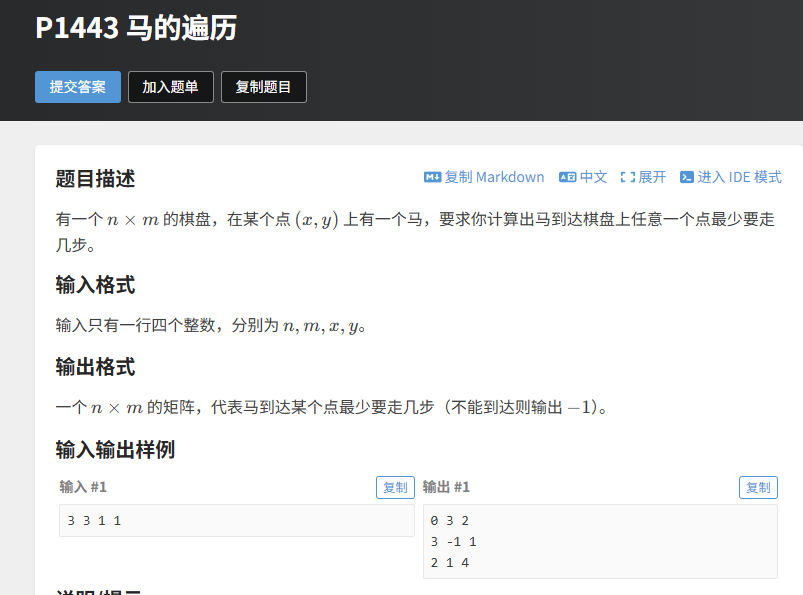
题目描述

给定一个 n×m 的棋盘，马初始在 (x,y) 位置，求马到达棋盘上任意点的最少步数（不能到达则输出 - 1）。

核心分析

这是 BFS 的入门题，核心考点是**"多方向扩展"**------ 马走 "日"，有 8 个移动方向，只需把方向数组改一下，其余逻辑和通用模板一致。

完整代码

cpp 复制代码 
#include <iostream>
#include <queue>
#include <cstring>
using namespace std;

typedef pair<int, int> PII;
const int N = 410;

int n, m, x, y;
int dist[N][N];
// 马的8个移动方向（走日）
int dx[] = {1, 2, 2, 1, -1, -2, -2, -1};
int dy[] = {2, 1, -1, -2, -2, -1, 1, 2};

void bfs() {
    memset(dist, -1, sizeof dist);
    queue<PII> q;
    q.push({x, y});
    dist[x][y] = 0;

    while (q.size()) {
        auto t = q.front();
        q.pop();
        int i = t.first, j = t.second;

        for (int k = 0; k < 8; k++) {
            int nx = i + dx[k], ny = j + dy[k];
            // 边界检查 + 未访问
            if (nx >= 1 && nx <= n && ny >= 1 && ny <= m && dist[nx][ny] == -1) {
                dist[nx][ny] = dist[i][j] + 1;
                q.push({nx, ny});
            }
        }
    }
}

int main() {
    cin >> n >> m >> x >> y;
    bfs();
    // 输出结果矩阵
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= m; j++) {
            cout << dist[i][j] << " ";
        }
        cout << endl;
    }
    return 0;
}

关键细节

  • 马的方向数组是本题的唯一难点，记住 "走日" 的 8 个组合即可；
  • 距离数组初始化为 - 1，起点置 0，扩展时每一步距离 + 1，天然满足 "最短步数"；
  • 无需提前退出，因为要计算所有点的距离，需遍历完整个队列。

2.2 进阶款：kotori 和迷宫（牛客网）

题目链接： https://ac.nowcoder.com/acm/problem/50041

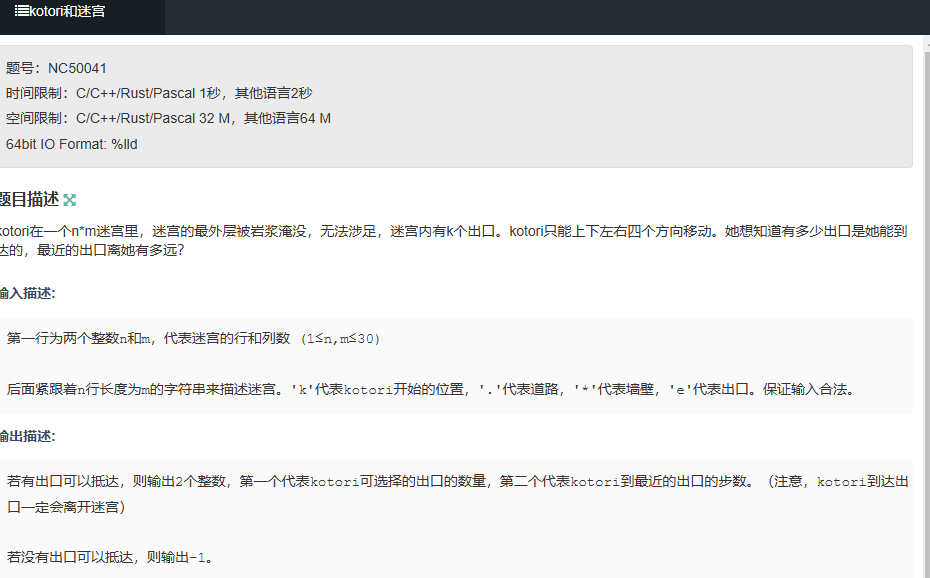
题目描述

n×m 的迷宫，最外层是岩浆（无法走），有 k 个出口（'e'），起点是 'k'，道路是 '.'，墙壁是 '*'。求能到达的出口数量，以及最近出口的步数（无法到达输出 - 1）。

核心分析

这道题在基础 BFS 上增加了 "多目标判断"：需要遍历所有出口，统计可达数量和最短距离。核心思路是：

  1. 先用 BFS 求出起点到所有点的最短距离；
  2. 遍历整个迷宫，筛选出标记为 'e' 且距离不为 - 1 的位置，统计数量和最小值。

完整代码

cpp 复制代码 
#include <iostream>
#include <queue>
#include <cstring>
#include <climits>
using namespace std;

typedef pair<int, int> PII;
const int N = 35;

int n, m, start_x, start_y;
char a[N][N];
int dist[N][N];

int dx[] = {0, 0, 1, -1};
int dy[] = {1, -1, 0, 0};

void bfs() {
    memset(dist, -1, sizeof dist);
    queue<PII> q;
    q.push({start_x, start_y});
    dist[start_x][start_y] = 0;

    while (q.size()) {
        auto t = q.front();
        q.pop();
        int i = t.first, j = t.second;

        for (int k = 0; k < 4; k++) {
            int nx = i + dx[k], ny = j + dy[k];
            // 边界 + 不是墙壁 + 未访问
            if (nx >= 1 && nx <= n && ny >= 1 && ny <= m && a[nx][ny] != '*' && dist[nx][ny] == -1) {
                dist[nx][ny] = dist[i][j] + 1;
                q.push({nx, ny});
            }
        }
    }
}

int main() {
    cin >> n >> m;
    // 读入迷宫，定位起点
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= m; j++) {
            cin >> a[i][j];
            if (a[i][j] == 'k') {
                start_x = i;
                start_y = j;
            }
        }
    }

    bfs();

    // 统计出口数量和最短距离
    int cnt = 0;
    int min_step = INT_MAX;
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= m; j++) {
            if (a[i][j] == 'e' && dist[i][j] != -1) {
                cnt++;
                min_step = min(min_step, dist[i][j]);
            }
        }
    }

    if (cnt == 0) {
        cout << -1 << endl;
    } else {
        cout << cnt << " " << min_step << endl;
    }

    return 0;
}

关键细节

  • 迷宫类问题的核心是**"合法路径判断"：本题中需排除墙壁（'*'）和岩浆（题目说最外层是岩浆，只需限制nx/ny**在 1~n/1~m 即可）；
  • 最短距离初始化用 INT_MAX（需包含<climits>），避免初始值干扰最小值计算；
  • 统计阶段要同时满足 "是出口" 和 "可达（距离≠-1）" 两个条件。

2.3 优化款：Catch That Cow（洛谷 USACO07OPEN）

题目链接： https://www.luogu.com.cn/problem/P1588

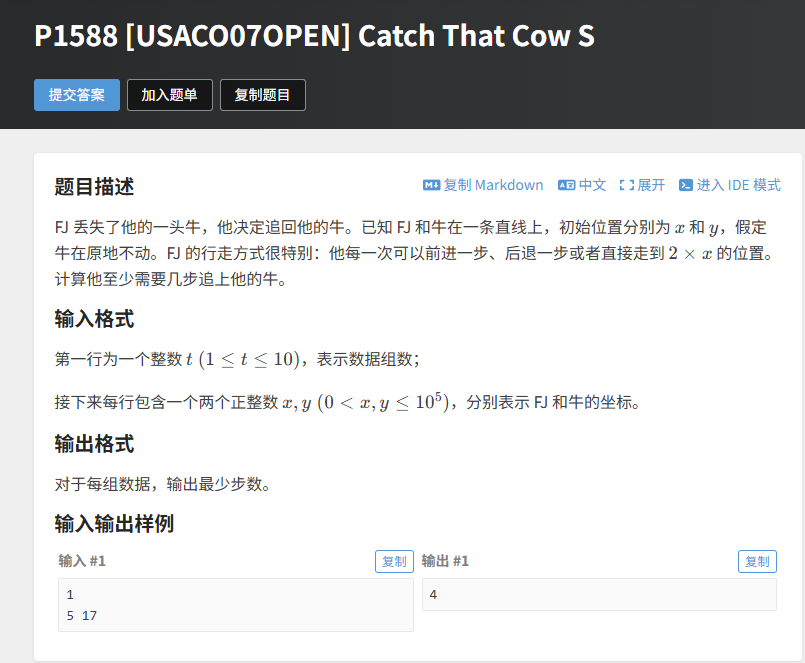
题目描述

FJ 和牛在一维直线上，初始位置 x 和 y（牛不动）。FJ 的移动方式：前进一步（x+1）、后退一步（x-1）、瞬移（x×2），求追上牛的最少步数。

核心分析

这是一维 BFS 的经典题，看似简单，但不剪枝会超时！因为 x 可能达到 1e5，盲目扩展会导致队列过大。核心优化点（剪枝策略）：

  1. 后退到负数：剪掉（退到负数再回来，步数一定更多）；
  2. 前进超过 y：剪掉（已经在牛右边，再前进只会离得更远）；
  3. 瞬移超过 2*y：剪掉（若 y 是偶数，瞬移到超过 y 不如先减到 y/2 再瞬移；若 y 是奇数，超过 y+1 也无意义）。

完整代码

cpp 复制代码 
#include <iostream>
#include <queue>
#include <cstring>
using namespace std;

const int N = 1e5 + 10;
int dist[N];
int x, y;

void bfs() {
    memset(dist, -1, sizeof dist);
    queue<int> q;
    q.push(x);
    dist[x] = 0;

    while (q.size()) {
        int t = q.front();
        q.pop();

        // 找到目标，提前退出
        if (t == y) return;

        // 扩展三种移动方式
        // 1. 前进一步
        if (t + 1 <= N - 10 && dist[t + 1] == -1) {
            dist[t + 1] = dist[t] + 1;
            q.push(t + 1);
        }
        // 2. 后退一步（不能为负）
        if (t - 1 >= 0 && dist[t - 1] == -1) {
            dist[t - 1] = dist[t] + 1;
            q.push(t - 1);
        }
        // 3. 瞬移（不超过2*y，避免无效扩展）
        if (t * 2 <= 2 * y && dist[t * 2] == -1) {
            dist[t * 2] = dist[t] + 1;
            q.push(t * 2);
        }
    }
}

int main() {
    int T;
    cin >> T;
    while (T--) {
        cin >> x >> y;
        bfs();
        cout << dist[y] << endl;
    }
    return 0;
}

关键细节

  • 一维 BFS 的队列存储的是 "位置值"，而非坐标对，简化了数据结构；
  • 剪枝是本题的核心：瞬移的**剪枝条件（t2 <= 2y）**能大幅减少队列大小，避免超时；
  • 多组数据时，每次 BFS 前要重置 dist 数组（memset），否则会继承上一组的结果。

2.4 高阶款：八数码难题（洛谷 P1379）

题目链接： https://www.luogu.com.cn/problem/P1379

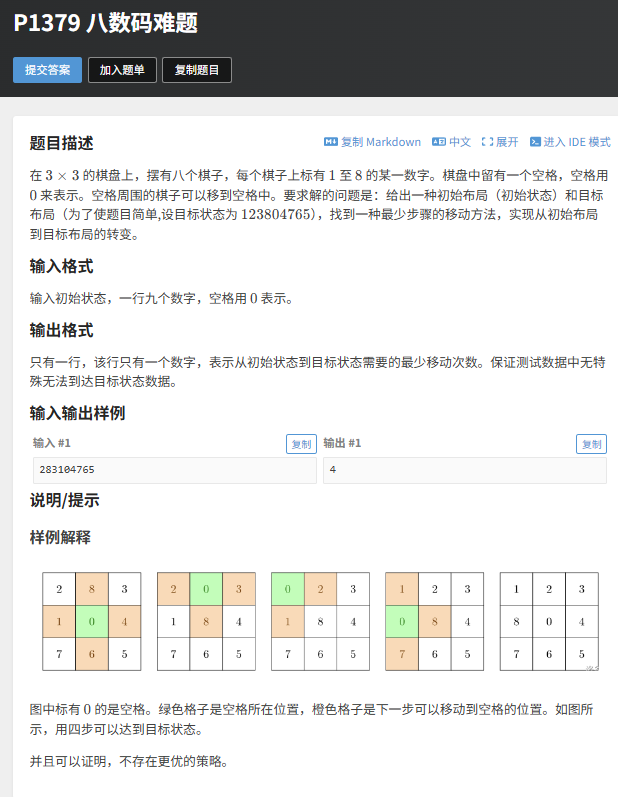
题目描述

3×3 棋盘上有 8 个棋子（1~8）和一个空格（0），空格周围的棋子可移动到空格。给定初始状态，求到目标状态（123804765）的最少步数。

核心分析

这是 BFS 的经典难题，核心难点是**"状态表示"** 和**"状态转换"**：

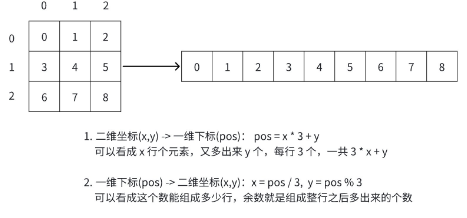
  1. 状态表示：把 3×3 棋盘转化为字符串（如初始状态 283104765 对应字符串 "283104765"），方便存储和哈希；
  2. 状态转换：找到空格的位置（pos），计算其在 3×3 棋盘中的二维坐标（x=pos/3，y=pos%3），然后交换空格与上下左右棋子的位置，生成新状态；
  3. 距离记录：用 **unordered_map<string, int>**存储每个状态的最短距离，避免重复访问。

完整代码

cpp 复制代码 
#include <iostream>
#include <queue>
#include <unordered_map>
using namespace std;

string aim = "123804765";
unordered_map<string, int> dist;

// 方向数组（上下左右）
int dx[] = {0, 0, 1, -1};
int dy[] = {1, -1, 0, 0};

void bfs(string start) {
    queue<string> q;
    q.push(start);
    dist[start] = 0;

    while (q.size()) {
        string t = q.front();
        q.pop();

        // 找到目标，提前退出
        if (t == aim) return;

        // 找到空格的位置
        int pos = t.find('0');
        int x = pos / 3, y = pos % 3;

        // 扩展四个方向
        for (int i = 0; i < 4; i++) {
            int nx = x + dx[i];
            int ny = y + dy[i];
            // 边界检查
            if (nx >= 0 && nx < 3 && ny >= 0 && ny < 3) {
                // 计算新状态的空格位置
                int new_pos = nx * 3 + ny;
                // 交换空格与相邻棋子
                string next = t;
                swap(next[pos], next[new_pos]);
                // 未访问过则更新距离
                if (!dist.count(next)) {
                    dist[next] = dist[t] + 1;
                    q.push(next);
                }
            }
        }
    }
}

int main() {
    string s;
    cin >> s;
    bfs(s);
    cout << dist[aim] << endl;
    return 0;
}

关键细节

  • 状态转换的核心是 "一维下标与二维坐标的转换"：pos = x*3 + y，x = pos/3，y = pos%3（这个技巧在网格类问题中高频使用）；
  • unordered_map 的 count 方法：判断状态是否已访问，避免重复入队；
  • 字符串的 find方法：快速定位空格（'0'）的位置，简化代码。

三、BFS 的扩展玩法 ------ 多源 BFS、01 BFS

除了基础 BFS，还有两种高频变种：多源 BFS 和01 BFS，它们是解决复杂问题的 "杀手锏"。

3.1 多源 BFS：矩阵距离（牛客网）

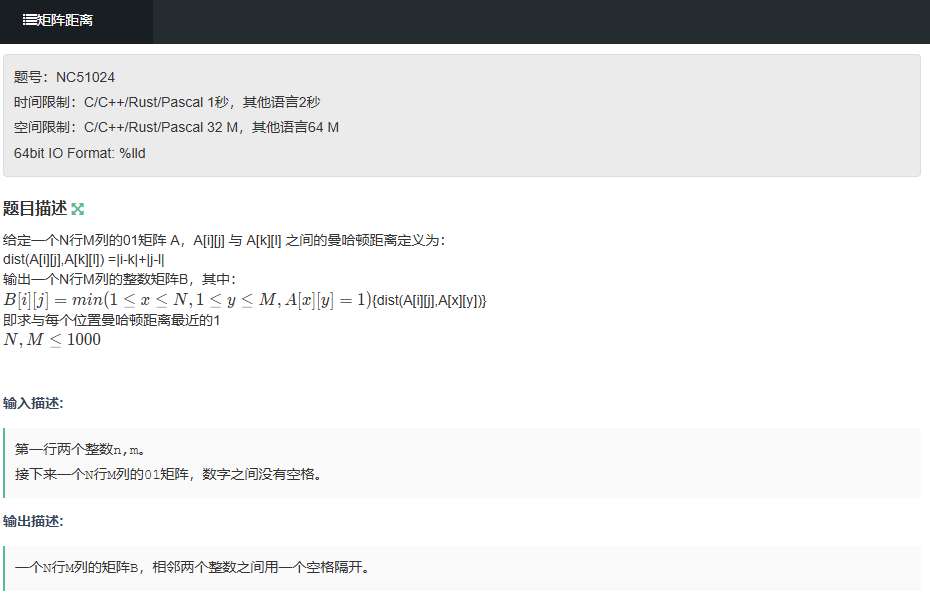
题目链接： https://ac.nowcoder.com/acm/problem/51024

核心思想

当问题有多个起点时，把所有起点一次性加入队列，视为 "超级源点"，然后按普通 BFS 扩展 ------ 本质是 "把多个单源 BFS 合并为一次遍历"，大幅降低时间复杂度。

典型场景

求矩阵中每个 0 到最近的 1 的曼哈顿距离（曼哈顿距离：|x1-x2| + |y1-y2|）。

核心代码片段

cpp 复制代码 
void bfs() {
    memset(dist, -1, sizeof dist);
    queue<PII> q;
    // 所有1的位置入队（多源起点）
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= m; j++) {
            if (a[i][j] == '1') {
                q.push({i, j});
                dist[i][j] = 0;
            }
        }
    }

    // 普通BFS扩展
    while (q.size()) {
        auto t = q.front();
        q.pop();
        int x = t.first, y = t.second;
        for (int i = 0; i < 4; i++) {
            int nx = x + dx[i], ny = y + dy[i];
            if (nx >= 1 && nx <= n && ny >= 1 && ny <= m && dist[nx][ny] == -1) {
                dist[nx][ny] = dist[x][y] + 1;
                q.push({nx, ny});
            }
        }
    }
}

3.2 01 BFS：小明的游戏（洛谷 P4554）

题目链接： https://www.luogu.com.cn/problem/P4554

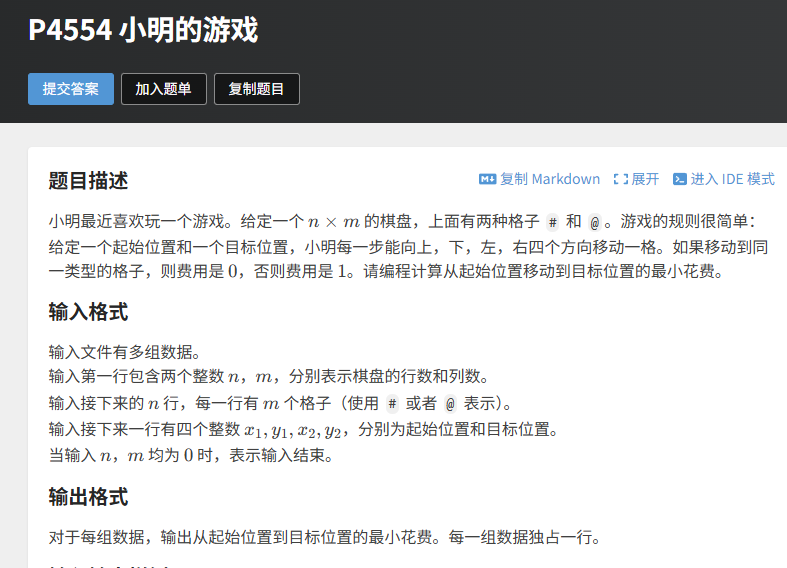
核心思想

当边权只有 0 和 1 时，用**双端队列（deque）**替代普通队列：

  • 边权为 0：新节点加入队头（优先扩展，保证距离最短）；
  • 边权为 1：新节点加入队尾（常规扩展）。这种方式能在 O (nm) 时间内求出最短路径，比 Dijkstra 算法更高效。

典型场景

棋盘移动，走相同类型格子费用 0，不同类型费用 1，求最小费用。

核心代码片段

cpp 复制代码 
int bfs() {
    memset(dist, -1, sizeof dist);
    deque<PII> q;
    q.push_back({x1, y1});
    dist[x1][y1] = 0;

    while (q.size()) {
        auto t = q.front();
        q.pop_front();
        int a = t.first, b = t.second;

        if (a == x2 && b == y2) return dist[a][b];

        for (int i = 0; i < 4; i++) {
            int nx = a + dx[i], ny = b + dy[i];
            if (nx >= 1 && nx <= n && ny >= 1 && ny <= m && dist[nx][ny] == -1) {
                if (g[a][b] == g[nx][ny]) {
                    // 边权0，加入队头
                    dist[nx][ny] = dist[a][b];
                    q.push_front({nx, ny});
                } else {
                    // 边权1，加入队尾
                    dist[nx][ny] = dist[a][b] + 1;
                    q.push_back({nx, ny});
                }
            }
        }
    }
    return -1;
}

四、BFS 的避坑指南 ------ 这些错误 90% 的人都会犯

  1. 忘记标记访问状态：导致节点重复入队，队列无限膨胀，超时或内存溢出；
  2. 边界判断错误：比如把 "nx <= n" 写成 "nx < n"，漏掉最后一行 / 列，导致结果错误；
  3. 多组数据未重置数组：dist、st 等数组继承上一组结果，逻辑混乱；
  4. 方向数组写错：比如把马的方向数组写漏，导致扩展不完整；
  5. 状态表示不当：如八数码用二维数组存储状态，无法哈希，导致重复访问。

总结

BFS 看似简单，但想要用得 "炉火纯青"，需要吃透底层逻辑，更要多练、多总结。希望这篇文章能帮你打通 BFS 的任督二脉，下次遇到搜索问题，能第一时间想到 "用 BFS 是不是更优？"------ 这才是真正掌握了这一算法的精髓。

最后，留一个小问题：八数码问题中，如果目标状态不固定，如何优化状态存储？欢迎在评论区交流～

相关推荐
小猪咪piggy1 小时前
【算法】day 20 leetcode 贪心
算法·leetcode·职场和发展
forestsea2 小时前
现代 JavaScript 加密技术详解：Web Crypto API 与常见算法实践
前端·javascript·算法
张洪权2 小时前
bcrypt 加密
算法
快手技术2 小时前
视频理解霸榜！快手 Keye-VL 旗舰模型重磅开源，多模态视频感知领头羊
算法
骑自行车的码农3 小时前
🍂 React DOM树的构建原理和算法
javascript·算法·react.js
CoderYanger3 小时前
优选算法-优先级队列（堆）：75.数据流中的第K大元素
java·开发语言·算法·leetcode·职场和发展·1024程序员节
希望有朝一日能如愿以偿3 小时前
力扣每日一题：能被k整除的最小整数
数据结构·算法·leetcode
Controller-Inversion3 小时前
力扣53最大字数组和
算法·leetcode·职场和发展
rit84324993 小时前
基于感知节点误差的TDOA定位算法
算法
热门推荐
01GitHub 镜像站点02BongoCat - 跨平台键盘猫动画工具03【保姆级教程】免费使用Gemini3的5种方法！免翻墙/国内直连04UV安装并设置国内源05安娜的档案(Anna’s Archive) 镜像网站/国内最新可访问入口（持续更新）06Linux下V2Ray安装配置指南07“我的电脑”图标没了怎么办 4种方法找回08Labelme从安装到标注：零基础完整指南09全球最强模型Grok4，国内已可免费使用！（附教程）10Gemini 3.0 Pro Preview 实测报告