目录
[1.1 上一篇概要:](#1.1 上一篇概要:)
[1.2 重点:](#1.2 重点:)
[1.3 举例:](#1.3 举例:)
[二、连续时间 PID](#二、连续时间 PID)
[2.1 连续时间形式](#2.1 连续时间形式)
[2.2 性能指标](#2.2 性能指标)
[三、从连续到离散:单片机/PLC 里 PID 怎么算?](#三、从连续到离散:单片机/PLC 里 PID 怎么算?)
[3.1 离散化思路](#3.1 离散化思路)
[四、位置式 PID:直接算"当前输出该多少"](#四、位置式 PID:直接算“当前输出该多少”)
[4.1 位置式 PID 的思路:](#4.1 位置式 PID 的思路:)
[4.2 典型离散形式(示意):](#4.2 典型离散形式(示意):)
[4.3 特点:](#4.3 特点:)
[五、增量式 PID:只算「这次比上次多给多少」](#五、增量式 PID:只算「这次比上次多给多少」)
[5.1 增量式 PID 的思路:](#5.1 增量式 PID 的思路:)
[5.2 典型写法:](#5.2 典型写法:)
[5.3 关键点:](#5.3 关键点:)
[六、位置式 vs 增量式:用 DC 电机做个直观对比](#六、位置式 vs 增量式:用 DC 电机做个直观对比)
[6.1 用位置式 PID:](#6.1 用位置式 PID:)
[6.2 用增量式 PID:](#6.2 用增量式 PID:)
[6.3 对比总结:](#6.3 对比总结:)
[6.4 工程建议:](#6.4 工程建议:)
[七、PID 伪代码](#七、PID 伪代码)
[7.1 设计通用 PID_t 结构体](#7.1 设计通用 PID_t 结构体)
[7.2 位置式 PID 更新函数(带反积分饱和 + 输出限幅)](#7.2 位置式 PID 更新函数(带反积分饱和 + 输出限幅))
[7.3 如果要做增量式 PID,要改哪一块?](#7.3 如果要做增量式 PID,要改哪一块?)
[8.1 单环 PID 的实战步骤](#8.1 单环 PID 的实战步骤)
[8.2 单环 PID 动图调参演示:](#8.2 单环 PID 动图调参演示:)
前言:
前面已经详细的介绍了开环反馈、闭环反馈和PID控制的详细内容,链接如下:
并且用「小明走路」把开环、闭环和 P / I / D 的直觉讲清楚了。
这一篇,我将从「故事」走向「工程」:
-
把 PID 放进标准控制框图里
-
看看它在连续域 / 离散域的几种写法
-
讲清 位置式 vs 增量式 PID
-
再聊聊串级(双环)PID 、防积分饱和、微分滤波、调参步骤
目标是:能直接写到单片机 / PLC / 电机控制 项目里。
一、从"小明走路"到通用控制对象
1.1 上一篇概要:
bash
目标 r(t)
↓
[−] → e(t) → [ 控制器 C(s) = PID ] → u(t) → [ 被控对象 G(s) ] → y(t)
↑ ↓
└─────────────── 反馈 ────────────────┘-
r(t):给定/参考值(比如:期望车速 1m/s、期望位置 10m、期望温度 60℃)
-
y(t):实际输出(编码器测的速度、位置,温度传感器的温度......)
-
e(t) = r(t) - y(t):误差
-
C(s):控制器,这里就是 PID
-
G(s):被控对象(电机+负载、车体动力学、加热炉等)
1.2 重点:
PID 本身只是个「误差算子」,关键是你给它什么误差,让它输出什么物理量。
1.3 举例:
-
位置控制:
-
e = 期望位置 - 实际位置 -
u = 期望速度/加速度或者PWM 占空比
-
-
速度控制:
-
e = 期望速度 - 实际速度 -
u = 电压 / 电流 / 转矩指令
-
二、连续时间 PID
2.1 连续时间形式
标准 PID 公式:
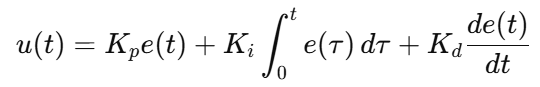
2.2 性能指标
1)指标量:
给系统一个阶跃目标(比如 0→1),你会关心这几件事:
-
**上升时间:**多久第一次冲到目标附近
-
**超调量:**最高点超过目标的百分比
-
**调节时间:**多久稳定在目标附近的某个误差带(比如 ±2%)
-
**稳态误差:**完全稳定后,还差多少
2)对应参数:
-
Kp :决定「敢不敢冲」,上升时间主要看它
-
Ki :最后能不能"抠干净误差",稳态误差看它
-
Kd :过冲和振荡压不压得住,看它
三、从连续到离散:单片机/PLC 里 PID 怎么算?
现实里我们的控制器 (MCU、DSP、PLC、上位机)都是离散的:
每隔一个固定采样周期
T,
读一次传感器 → 算一次PID → 输出一次控制量。
3.1 离散化思路
把连续 PID 公式里的积分、微分用差分近似:
1)积分:
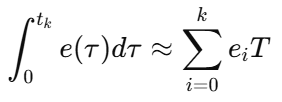
2)微分:
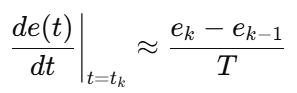
于是得到了两个非常常见的数字 PID 形式:位置式 和增量式。
四、位置式 PID:直接算"当前输出该多少"
4.1 位置式 PID 的思路:
直接算出当前时刻的"绝对输出" u(k)。
4.2 典型离散形式(示意):
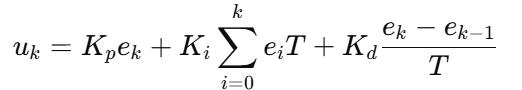
4.3 特点:
-
每次都用到从头积累的积分和;
-
控制器直接吐出一个绝对控制量
u_k:-
如:目标 PWM 占空比 = 63%
-
目标转矩指令 = 1.3 N·m
-
-
适合**「控制量本身就有明确物理意义」**的场景:
-
温度控制:给出的就是当前加热功率百分比
-
位置控制:直接给「目标位置」命令(伺服内部再处理)
-
1)优点:
-
形式直观,和数学公式最接近;
-
输出容易理解和监控(你看到的就是此刻控制器的真实意图)。
2)缺点:
-
对 积分饱和 比较敏感:积分和从 0 累到 k,稍微没限制就会爆;
-
一旦内部某次计算错得很离谱(传感器瞬间异常),
u可能一下飞很远。
五、增量式 PID:只算**「** 这次比上次多给多少**」**
5.1 增量式 PID 的思路:
我不直接告诉你"这次要输出多少",
我只告诉你「在上次基础上应加/减多少」。
5.2 典型写法:
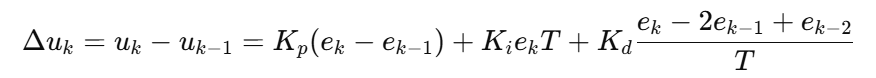
然后:
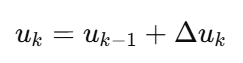
5.3 关键点:
-
只用到了最近三次误差
e_k, e_{k-1}, e_{k-2} -
公式中没有显式的「积分和」------它被"吃进"系数里了
-
只要前几次已经算过了,后面每步计算量很小,很适合 MCU 实时跑
增量式 PID 输出的是「控制量的增量」,不是绝对值。
六、位置式 vs 增量式:用 DC 电机做个直观对比
假设:
-
现在电机实际转速 50 RPM
-
我们想升到 60 RPM
6.1 用位置式 PID:
-
控制器直接算出一个"目标输出"
u_k -
比如 u_k 对应的 PWM 占空比是 35%,直接发 35%
6.2 用增量式 PID:
-
控制器算出:
"在上一次基础上,应该再提高一点输出"
-
比如 Δu = +3%
-
于是新输出 =
u_k = u_{k-1} + Δu = 32% + 3% = 35%
6.3 对比总结:
| 维度 | 位置式 PID | 增量式 PID |
|---|---|---|
| 输出含义 | 直接给出当前「绝对控制量」 u(k) | 给出「控制量增量」 Δu(k) |
| 历史依赖 | 用到从 0 到 k 的积分和 | 只用最近 2~3 个误差 |
| 数值稳定性 | 一次计算异常可能让 u 飙很大 | 异常只影响这一小步的 Δu,相对更鲁棒 |
| 实现复杂度 | 公式简单,但要自己管好积分 | 公式稍复杂,但更适合数字实现 |
| 常见应用 | 温控、慢变量、直接给位置/功率命令 | 电机、电流控制、执行器只接收"增量"的场景 |
6.4 工程建议:
-
MCU 上带 PWM 控制直流电机、伺服、步进:
→ 增量式 PID 很香(少算、抗异常、方便做限幅)
-
做简单温控、小车位置环之类的:
→ 位置式 PID 足够,逻辑更直观。
七、PID 伪代码
前面我们一直在讲:P / I / D 在数学上、物理上分别干什么。真正落地到 MCU / STM32 / PLC / 上位机时,就要把这些东西装进一个结构体 + 若干函数里,让它像一个黑盒控制器一样反复调用。
这一章我们做三件事:
-
设计一个通用、可复用的
PID_t结构体; -
写一个「位置式 PID + 反积分饱和 + 输出限幅」的更新函数;
-
顺带说明:如果想改成增量式 PID,只需要改哪一块。
7.1 设计通用 PID_t 结构体
1)完整结构体代码
cpp
typedef struct {
/* ★ PID 参数 */
float Kp; // 比例系数
float Ki; // 积分系数
float Kd; // 微分系数
/* ★ 输入输出相关变量 */
float set; // 当前目标值(setpoint)
float fdb; // 当前反馈值(feedback)
/* ★ 误差相关(支持位置式 + 增量式) */
float err; // 当前误差 e(k)
float err_last; // 上一次误差 e(k-1)
float err_llast; // 上上次误差 e(k-2),增量式 PID 会用到
/* ★ 积分项状态(位置式 PID 用) */
float integral; // 积分和 ∑ e*dt
/* ★ 控制输出 */
float out; // 当前输出 u(k)
/* ★ 输出限幅 */
float out_min; // 输出下限(例如:-100% PWM)
float out_max; // 输出上限(例如:+100% PWM)
/* ★ 积分限幅(防积分饱和 / 风up) */
float integ_min; // 积分下限
float integ_max; // 积分上限
} PID_t;7.2 位置式 PID 更新函数(带反积分饱和 + 输出限幅)
1)完整函数代码
cpp
void PID_Pos_Update(PID_t *pid, float set, float fdb, float dt)
{
/* 0)基础防御:空指针、异常 dt */
if (pid == NULL) return;
if (dt <= 0.0f) dt = 1e-3f; // 防止除 0,给个极小值兜底
/* 1)保存目标值和反馈值(便于调试、上位机显示) */
pid->set = set;
pid->fdb = fdb;
/* 2)计算当前误差 e(k) */
float err = set - fdb;
pid->err = err;
/* 3)积分项:累加误差 * dt,并进行积分限幅(防 windup) */
pid->integral += err * dt;
if (pid->integral > pid->integ_max)
pid->integral = pid->integ_max;
if (pid->integral < pid->integ_min)
pid->integral = pid->integ_min;
/* 4)微分项:最简单的后向差分 (e(k) - e(k-1)) / dt */
float derivative = (err - pid->err_last) / dt;
/* 5)三项相加得到"位置式 PID"的绝对输出 u(k) */
float out = pid->Kp * err
+ pid->Ki * pid->integral
+ pid->Kd * derivative;
/* 6)输出限幅:把 u(k) 夹在允许范围内 */
if (out > pid->out_max) out = pid->out_max;
if (out < pid->out_min) out = pid->out_min;
/* 7)保存输出和当前误差,为下一次调用做准备 */
pid->out = out;
pid->err_last = err;
}7.3 如果要做增量式 PID,要改哪一块?
1)核心思想
位置式:算"这次应该给多少" → 直接得到
u(k)增量式:算"这次比上次多给多少" → 只给
Δu(k)
也就是:
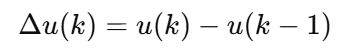
-
控制器内部保存的是
u(k-1); -
每次算出一个增量
Δu(k),然后
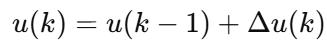
在结构体不变的前提下,只要把第 5 步"三项相加"那一行改写成 Δu 的形式 即可,最后 pid->out += Δu。
2)简化版增量式伪代码(思路展示)
cpp
void PID_Inc_Update(PID_t *pid, float set, float fdb, float dt)
{
if (pid == NULL) return;
if (dt <= 0.0f) dt = 1e-3f;
pid->set = set;
pid->fdb = fdb;
float err = set - fdb;
/* ① 增量式的核心:只算 Δu,而不是绝对 u(k) */
float de = err - pid->err_last; // e(k) - e(k-1)
float du_p = pid->Kp * de; // 比例增量
float du_i = pid->Ki * err * dt; // 积分增量(也可以做积分限幅)
float du_d = pid->Kd * (de / dt); // 微分增量(简化写法)
float du = du_p + du_i + du_d;
/* ② 累加得到新输出 u(k) */
float out = pid->out + du;
/* ③ 输出限幅 */
if (out > pid->out_max) out = pid->out_max;
if (out < pid->out_min) out = pid->out_min;
/* ④ 更新状态 */
pid->out = out;
pid->err_last = err;
}八、参数整定总结(含动图变化)
8.1 单环 PID 的实战步骤
-
只开 P,关掉 I/D
-
让系统对一个阶跃目标(比如位置从 0→1)做响应
-
从小到大调 Kp:
-
Kp 小:慢但稳
-
Kp 大到某个程度:开始出现振荡/超调
-
-
记下「刚开始振荡前」那一档 Kp
-
-
加一点 I,消除稳态误差
-
看稳态时有没有残余误差
-
从比较小的 Ki 开始加:
-
如果误差消得更干净,超调还可接受 → 不错
-
超调/振荡明显变严重 → 把 Ki 降一点,或者 Kp 小调
-
-
-
必要时加 D,抑制超调
-
如果超调太大、振荡收不住,可以逐步增加 Kd
-
Kd 合理时:曲线会"圆润"、不过分冲击
-
如果噪声明显或响应开始变"迟钝",说明 Kd 过大或采样太慢
-
-
最后加入各种工程限制
-
输出限幅
-
积分限幅 / 条件积分 / anti-windup
-
D 项滤波
-
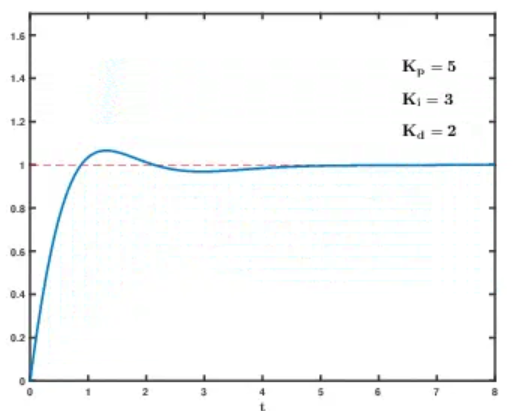
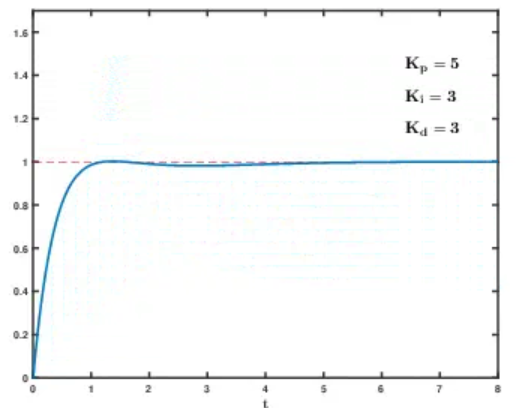
8.2 单环 PID 动图调参演示:
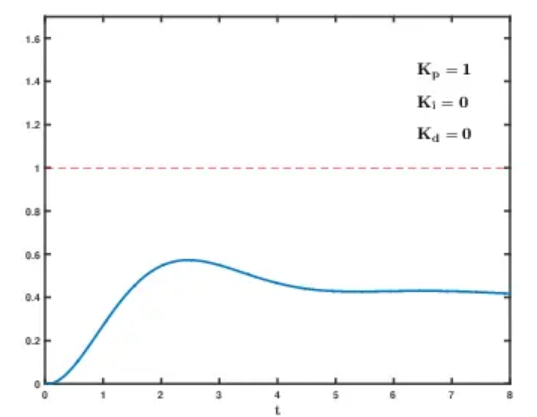
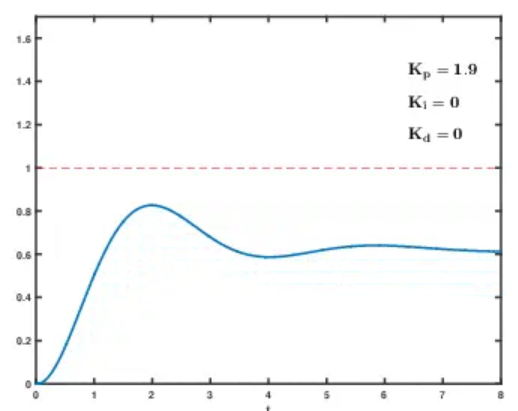
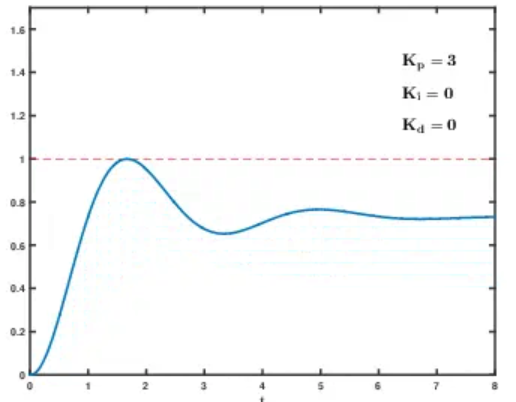
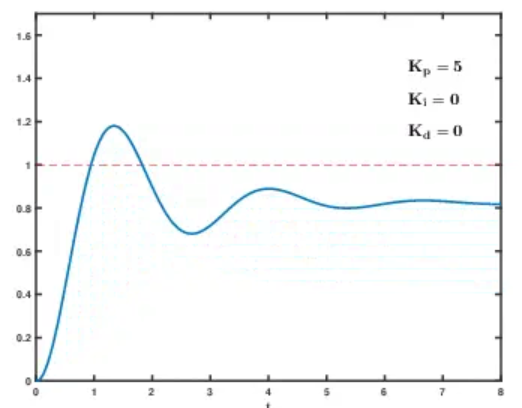
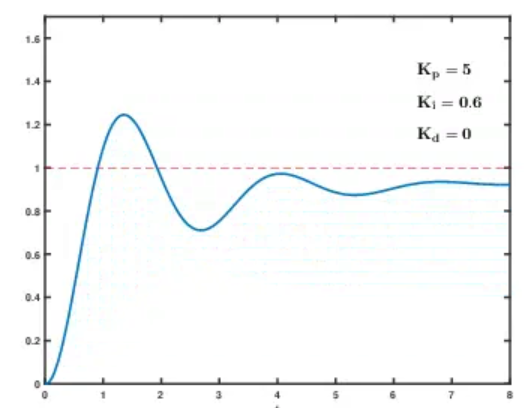
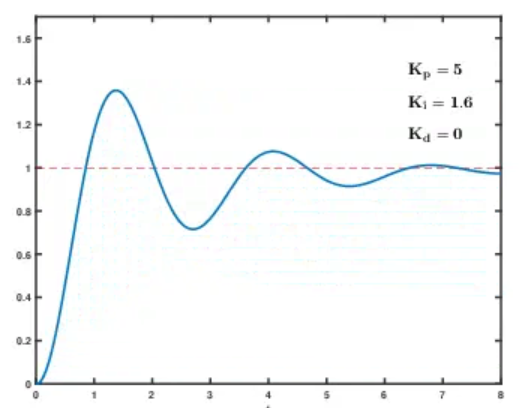
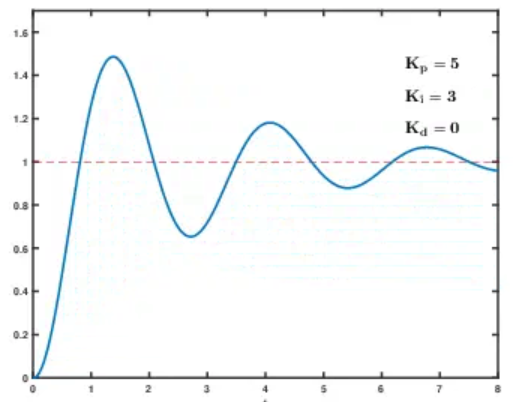
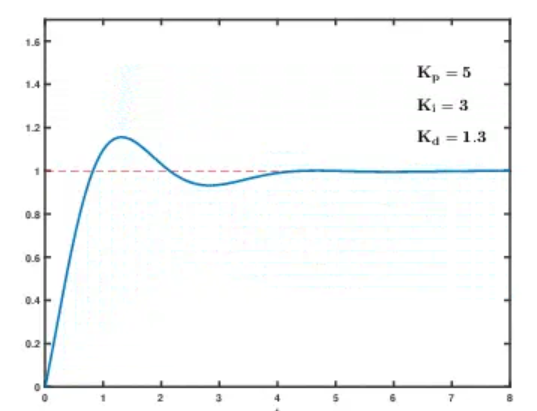
九、总结
1️⃣ 先问:我到底在控什么?
-
控位置 / 姿态 / 温度 / 转速 / 电流 / 扭矩?
-
目标、反馈、输出三种物理量分别是什么?
2️⃣ 再问:我用的是哪种 PID?
-
连续 / 离散?采样周期多少?
-
位置式 / 增量式?
3️⃣ 最后问:当前问题是 P/I/D 哪一环的锅?
-
响应太慢 → 多半是
Kp太小,或者采样太慢 -
静差大、拖尾明显 → 该考虑
Ki -
超调、振荡严重 → 看看
Kd和积分项,是不是该加阻尼、减积分、加滤波
学习完本章,把这套问法训练成条件反射,大家以后调PID参数就会更得心应手!