CW32L012的PID温度控制——算法基础

一、什么是PID 控制算法

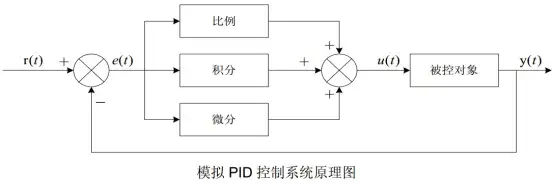
PID 控制算法是比例（Proportional）- 积分（Integral）- 微分（Derivative） 控制的简称，是工业控制、嵌入式系统中最经典、应用最广泛的闭环控制算法。它的核心思想是通过偏差（设定值与实际值的差值）的比例、积分、微分三个环节的加权组合，计算出控制量，使系统的实际输出快速、稳定地逼近设定值。

二、核心公式（连续域）

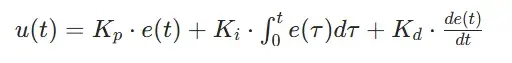
比例环节（P）

核心作用：即时响应偏差，偏差越大，控制量越大。
缺点：仅用 P 控制会存在稳态误差（系统稳定后，实际值与设定值仍有差距）；Kp过大会导致系统震荡。

积分环节（I）

核心作用：累积历史偏差，只要存在偏差，积分项就会持续增大，直到偏差为 0，从而消除稳态误差。
缺点：积分累积会导致系统超调（实际值超过设定值），甚至震荡；系统启动初期积分饱和会影响响应速度。

微分环节（D）

核心作用：预测偏差变化趋势，偏差变化越快，微分项输出越大，提前抑制偏差的变化（类似 "阻尼" 作用）。
缺点：对噪声敏感（传感器的微小波动会被放大）；Kd过大会导致系统响应迟缓。

离散化公式（嵌入式系统常用）

嵌入式 MCU 是离散采样系统 ，无法直接计算连续的积分和微分，需要将上述的连续域PID 公式离散化 ，用数值积分 和数值微分 替代连续运算，得到离散 PID 公式。

设系统采样周期为 Ts，第 k 次采样时刻的偏差为 e(k)=r(k)-y(k)（设定值-实际采样值），则离散 PID 有两种常用形式：

位置式PID

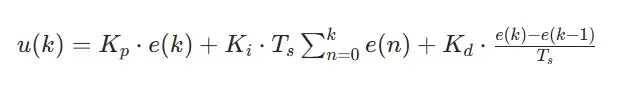
特点：输出 u(k) 是绝对控制量，也就是阀门开度（如电机的目标占空比、舵机的目标角度）。

C语言代码(通用)：

复制代码

typedef struct {
    float kp;          // 比例系数
    float ki;          // 积分系数
    float kd;          // 微分系数
    float set_point;   // 设定值
    float feedback;    // 反馈值
    float error;       // 当前误差 (set_point - feedback)
    float error_sum;   // 误差积分和（防止积分饱和）
    float error_prev;  // 上一次误差（微分用）
    float output_max;  // 输出最大值
    float output_min;  // 输出最小值
} PID_Positional;
/**
- @brief 位置式 PID 核心计算（无初始化函数，参数需外部赋值）
- @param pid: 位置式 PID 结构体指针
- @param set_point: 设定值
- @param feedback: 反馈值
- @return 位置式 PID 输出值
*/
float PID_Positional_Calc(PID_Positional *pid, float set_point, float feedback) {
    if (pid == NULL) return 0.0f;
    // 更新设定值和反馈值
    pid->set_point = set_point;
    pid->feedback = feedback;
    // 计算当前误差
    pid->error = pid->set_point - pid->feedback;
    // 积分项（带积分限幅，防止积分饱和）
    pid->error_sum += pid->error;
    // 积分限幅：根据输出限幅和 ki 动态约束（也可直接赋值固定值）
    float integral_max = (pid->output_max / pid->ki) * 0.8f;
    float integral_min = (pid->output_min / pid->ki) * 0.8f;
    if (pid->error_sum > integral_max) pid->error_sum = integral_max;
    if (pid->error_sum < integral_min) pid->error_sum = integral_min;
    // 位置式 PID 核心公式
    float output = pid->kp * pid->error +                    // 比例项
                   pid->ki * pid->error_sum +                // 积分项
                   pid->kd * (pid->error - pid->error_prev); // 微分项
    // 输出限幅
    if (output > pid->output_max) output = pid->output_max;
    if (output < pid->output_min) output = pid->output_min;
    // 更新上一次误差
    pid->error_prev = pid->error;
    return output;
}

2.增量式 PID

计算相邻两次控制量的差值 Δ u(k)，公式推导：

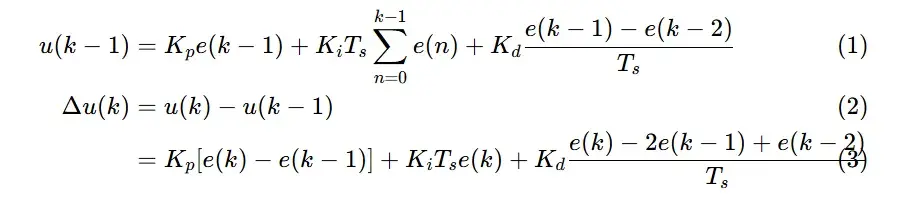
特点：输出Δ u(k) 是控制量增量，只需叠加到上一次的控制量上（在上一次的控制输出上进行加减）：u(k)=u(k-1)+Δ u(k)。

C语言代码（通用）：

复制代码

typedef struct {
    float kp;          // 比例系数
    float ki;          // 积分系数
    float kd;          // 微分系数
    float set_point;   // 设定值
    float feedback;    // 反馈值
    float error;       // 当前误差 (set_point - feedback)
    float error_prev1; // 前1次误差
    float error_prev2; // 前2次误差
    float output_inc;  // 增量输出
    float output_max;  // 输出最大值（用于增量限幅）
    float output_min;  // 输出最小值（用于增量限幅）
} PID_Incremental;
/**
@brief 增量式 PID 核心计算（无初始化函数，参数需外部赋值）
@param pid: 增量式 PID 结构体指针
@param set_point: 设定值
@param feedback: 反馈值
@return 增量式 PID 输出增量
*/
float PID_Incremental_Calc(PID_Incremental *pid, float set_point, float feedback) {
    if (pid == NULL) return 0.0f;
    // 更新设定值和反馈值
    pid->set_point = set_point;
    pid->feedback = feedback;
    // 计算当前误差
    pid->error = pid->set_point - pid->feedback;
    // 增量式 PID 核心公式
    pid->output_inc = pid->kp * (pid->error - pid->error_prev1) +          // 比例增量
                      pid->ki * pid->error +                              // 积分增量
                      pid->kd * (pid->error - 2*pid->error_prev1 + pid->error_prev2); // 微分增量
    // 增量限幅（避免单次增量过大）
    float inc_max = (pid->output_max - pid->output_min) / 2;
    if (pid->output_inc > inc_max) pid->output_inc = inc_max;
    if (pid->output_inc < -inc_max) pid->output_inc = -inc_max;
    // 更新误差历史（前2次 → 前1次，前1次 → 当前）
    pid->error_prev2 = pid->error_prev1;
    pid->error_prev1 = pid->error;
    return pid->output_inc;
}

三、嵌入式系统如何使用PID控制算法？

建立闭环反馈

明确被控对象

被控对象：比如温度、机器人关节、直流电机转速等；

选择合适的采样周期对被控变量进行采样

采集能反应被控对象当前状态的信号

采样周期的选择依据：

香农采样定理：采样频率至少是被控对象最高变化频率的 2 倍，避免信号混叠；
被控对象响应速度：比如直流电机响应速度为 ms 级，采样周期设置为1~10ms ；温度这类慢响应对象，采样周期设置为1~5s；

由此我们得到了被控对象温度的实际温度

PID运算出输出量

将目标值和采样值送入PID公式进行计算

需要注意：

抗积分饱和：当 PID 输出达到执行器最大 / 最小量程时，停止积分累加；
积分分离：当误差|ek|大于设定阈值时，暂停积分项运算，避免积分饱和导致的超调；

输出到执行器

将PID公式运算出来的结果作用到输出执行器

需要注意：

数值限幅：运算后必须将输出量限制在执行器的有效范围（比如 PWM 占空比 0~100%、DAC 输出 0~4095），避免输出超限损坏执行器；

PID参数的调参（Kp,Ki,Kd）

建立好闭环反馈环节后就可以对PID参数进行整定了，我们实际最多使用的是经验试凑法，这里只分享试凑法：

试凑法的核心逻辑：先调 P，再调 I，最后调 D，每次只改一个参数，观察系统响应，逐步逼近最优值。

只调比例环节（P），关闭 I 和 D

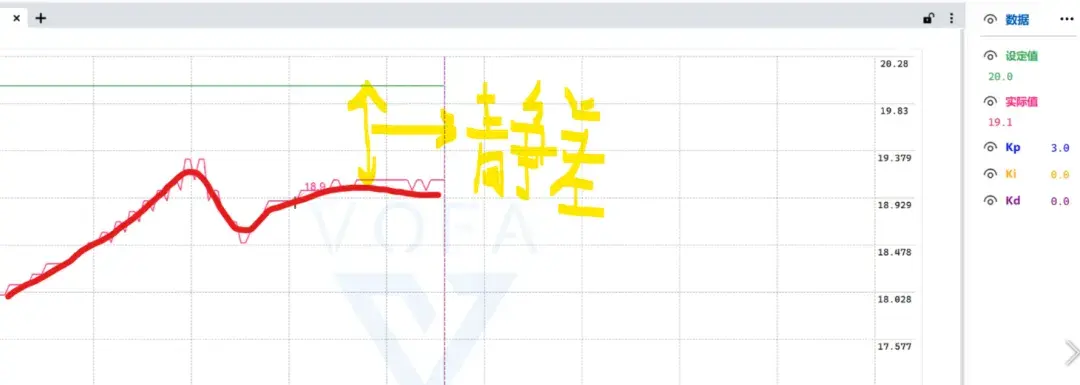
Ki=0，Kd=0，K_p 从 0 开始缓慢增大；直到响应较快，实际值快速接近设定值，轻微震荡后稳定，稳态误差较小

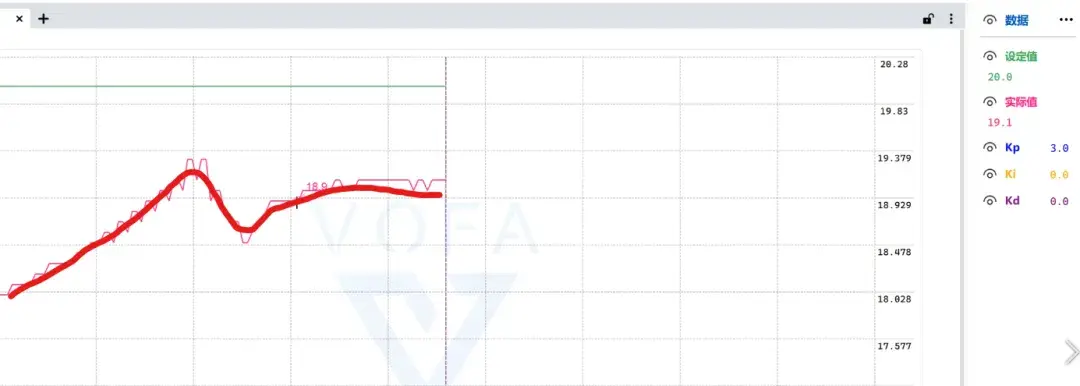
（此时可能会有静态误差，即输出一直达不到目标值这种情况）

Kp过大-->系统可能会震荡
Kp过小-->系统响应较慢, 可能达不到目标值

加入积分环节（I），消除稳态误差

为了消除静态误差，加入积分环节，在Kp已有的基础上，Kd=0，加入Ki，Ki 从 0 开始缓慢增大，直到系统能消除静态误差，并且不发生震荡

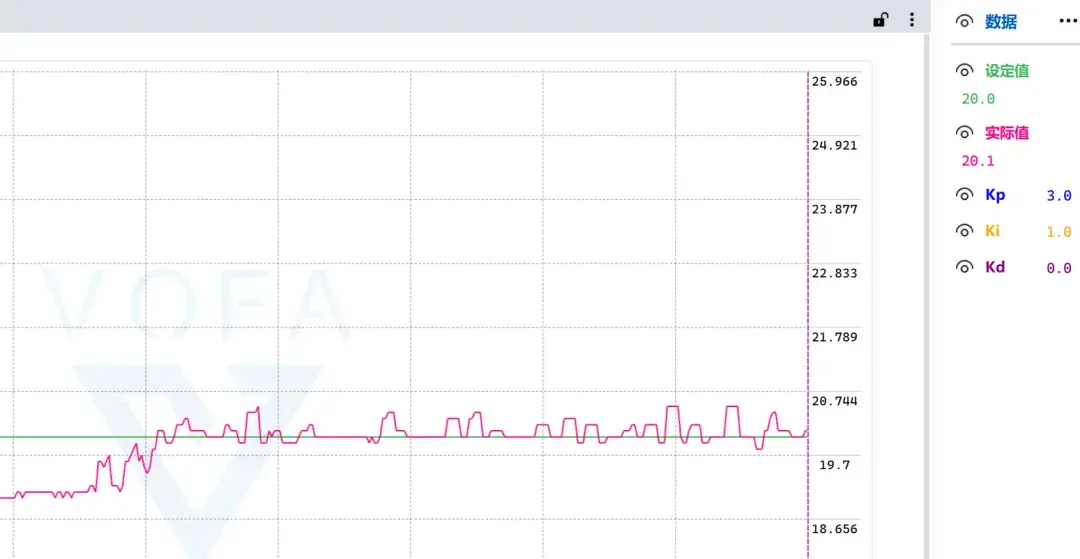
（要注意抗积分饱和，不然系统极易发生震荡）

Ki过大-->系统可能会震荡
Ki过小-->系统依旧有静差

加入微分环节（D），加快响应

若已达到预期的控制效果可不引入微分环节。

若未达到预期的控制效果，可以在前面的基础上使Kid从 0 开始缓慢增大，直到超调大幅减小，响应速度基本不变，系统快速稳定。