
本文给出三维空间中雷达与IMU(惯性测量单元)数据融合的MATLAB仿真程序,采用扩展卡尔曼滤波(EKF) 实现高精度位置、速度和姿态估计。
原创程序,非AI生成,带中文注释,可定制、讲解
文章目录
程序详解
核心功能
- 雷达测量 :提供极坐标观测数据
- 距离(r)
- 俯仰角(elevation)
- 方位角(azimuth)
- IMU测量 :6自由度惯性数据
- 三轴加速度
- 三轴角速度
系统估计10维状态向量:
- 位置(3维):p = [x, y, z]ᵀ
- 速度(3维):v = [vₓ, vᵧ, vᵤ]ᵀ
- 姿态四元数(4维):q = [q₀, q₁, q₂, q₃]ᵀ
核心数学模型
- 状态方程(预测模型)
位置更新:
p(k+1) = p(k) + v(k)·Δt + 0.5·a_nav·Δt²速度更新:
v(k+1) = v(k) + a_nav·Δt其中,导航系加速度通过IMU比力转换:
a_nav = R_nb · f_b + gR_nb:体坐标系到导航系的旋转矩阵(由四元数计算)f_b:IMU测量的比力(体轴加速度)g:重力加速度向量 [0, 0, -9.81]ᵀ
姿态更新(四元数):
q(k+1) = q(k) ⊗ Δq
Δq = [1; 0.5·ω_b·Δt] (小角度近似)ω_b:IMU测量的角速度⊗:四元数乘法
-
四元数到旋转矩阵
R_nb(q) = [q₀²+q₁²-q₂²-q₃² 2(q₁q₂-q₀q₃) 2(q₁q₃+q₀q₂) ]
[2(q₁q₂+q₀q₃) q₀²-q₁²+q₂²-q₃² 2(q₂q₃-q₀q₁) ]
[2(q₁q₃-q₀q₂) 2(q₂q₃+q₀q₁) q₀²-q₁²-q₂²+q₃²] -
雷达观测方程
极坐标观测模型:
z = [r ] = [||p - p_radar|| ]
[el ] [atan2(dz, √(dx² + dy²)) ]
[az ] [atan2(dy, dx) ]其中:
[dx, dy, dz]ᵀ = p - p_radar(目标相对雷达的位置差)r:斜距el:俯仰角az:方位角
观测雅可比矩阵 H(3×10):
对位置的偏导数:
∂r/∂p = [dx, dy, dz] / r
∂el/∂p = [-dx·dz/(r²·ρ), -dy·dz/(r²·ρ), ρ/r²]
∂az/∂p = [-dy/ρ², dx/ρ², 0]其中 ρ = √(dx² + dy²)
对速度和姿态的偏导数为0。
- EKF递推公式
预测步:
x̂⁻(k) = f(x̂⁺(k-1), u(k))
P⁻(k) = F(k)·P⁺(k-1)·F(k)ᵀ + Q更新步:
K(k) = P⁻(k)·H(k)ᵀ·[H(k)·P⁻(k)·H(k)ᵀ + R]⁻¹
x̂⁺(k) = x̂⁻(k) + K(k)·[z(k) - h(x̂⁻(k))]
P⁺(k) = [I - K(k)·H(k)]·P⁻(k)其中:
F:状态转移雅可比矩阵(通过有限差分计算)H:观测雅可比矩阵Q:过程噪声协方差R:测量噪声协方差K:卡尔曼增益
-
噪声参数
Q = diag([Qₚ, Qᵥ, Qᵩ]) (过程噪声)
R = diag([σᵣ², σₑₗ², σₐᵤ²]) (测量噪声)
运行结果
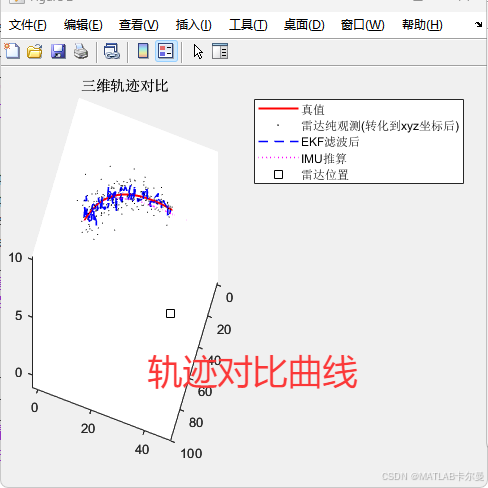
真实轨迹、雷达跟测的轨迹、INS推算轨迹、滤波后的轨迹,对比图:
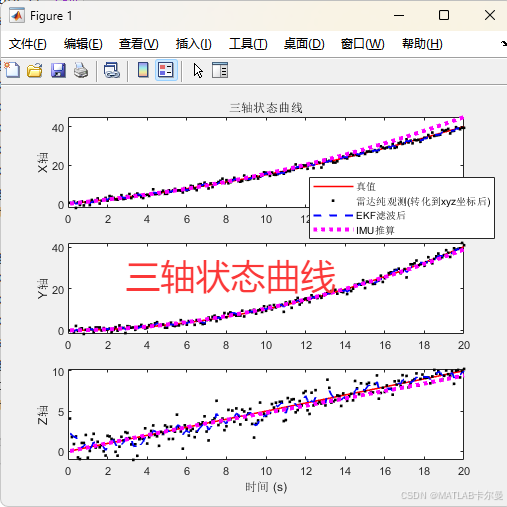
三维状态,分别显示的曲线:
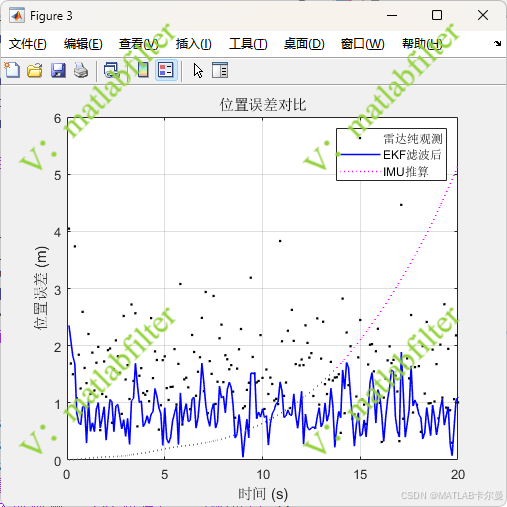
位置误差输出:
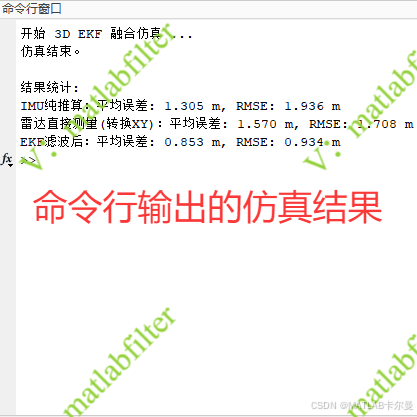
结果:
MATLAB源代码
完整代码如下:
matlab
% 三维空间中,雷达数据与IMU的融合,雷达观测距离、俯仰角、方向角,IMU包括6维(加速度与角速度)
% 3D 雷达(r,el,az) + IMU(3 acc, 3 gyro) 融合 - EKF (位置、速度、四元数)
% 作者:matlabfilter(V同号),接定位与导航、滤波相关的matlab代码定制
% 2025-11-25/Ver1
clear; close all; clc;
rng(0);
%% 仿真参数
dt = 0.1;
N = 200;
g = [0; 0; -9.81]; % 重力 (导航系:z向上为正则用 [0;0;-9.81])
%% 初始真值(目标运动与姿态)
true_p = [0; 0; 0]; % 初始位置 m
true_v = [1; 0; 0.5]; % 初始速度 m/s
% 初始姿态(单位四元数 [q0; qv],这里设为无旋转)
true_q = [1; 0; 0; 0];
% 给定目标加速度(惯性系)与角速度(体轴)时间序列(可自行修改)
% 这里做个简单示例:恒定小加速度和缓慢偏航
acc_inertial = repmat([0.1; 0.2; 0.0], 1, N); % 真值惯性加速度(仅用于生成真轨迹)
angvel_body = repmat([0; 0; 0.01], 1, N); % 真值角速度(rad/s)
%% 雷达位置(固定)
radar_pos = [50; 100; 10];
%% 传感器噪声
sigma_acc = 0.05; % m/s^2 (加速度传感器噪声标准差)
sigma_gyro = 0.005; % rad/s (陀螺噪声)
sigma_r = 1.0; % 测距误差,米
sigma_el = 0.01; % 俯仰角观测误差,弧度
sigma_az = 0.01; % 方位角观测误差,弧度
%% EKF 初值:状态与协方差
% 状态 x = [p(3); v(3); q(4)]
x_est = [true_p + [1; -1; 0.5]; % 初位置有偏差
true_v + [0.5; -0.5; 0];
1; 0; 0; 0]; % 初四元数(单位)
P = diag([1,1,1, 1,1,1, 0.01,0.01,0.01,0.01]);
%% 过程噪声协方差 Q(设计)
% 过程 Q 对应位置/速度/姿态不确定性,依据 IMU 噪声近似构造
Qp = 0.1 * eye(3);
Qv = 0.5 * eye(3);
Qq = 1e-4 * eye(4);
Q = blkdiag(Qp, Qv, Qq);
%% 测量噪声 R (r,el,az)
R = diag([sigma_r^2, sigma_el^2, sigma_az^2]);
%% 存储
true_ps = zeros(N,3);
est_ps = zeros(N,3);
imu_dead_ps = zeros(N,3); % 仅IMU死推
meas_ps = zeros(N,3); % 雷达转换后的点 (用于绘图)
%% 便捷函数:四元数乘法、四元数到旋转矩阵
quat_mul = @(q1,q2) [ q1(1)*q2(1) - q1(2:4)'*q2(2:4);
q1(1)*q2(2:4) + q2(1)*q1(2:4) + cross(q1(2:4), q2(2:4)) ];
quat_to_rotm = @(q) ( ...
[ q(1)^2+q(2)^2-q(3)^2-q(4)^2, 2*(q(2)*q(3)-q(1)*q(4)), 2*(q(2)*q(4)+q(1)*q(3));
2*(q(2)*q(3)+q(1)*q(4)), q(1)^2-q(2)^2+q(3)^2-q(4)^2, 2*(q(3)*q(4)-q(1)*q(2));
2*(q(2)*q(4)-q(1)*q(3)), 2*(q(3)*q(4)+q(1)*q(2)), q(1)^2-q(2)^2-q(3)^2+q(4)^2 ] );完整代码:
https://download.csdn.net/download/callmeup/92410348
或:
如需帮助,或有导航、定位滤波相关的代码定制需求,请点击下方卡片联系作者