通感一体化(ISAC)波形设计的实验验证研究
T. Xu, F. Liu, C. Masouros and I. Darwazeh, "An Experimental Proof of Concept for Integrated Sensing and Communications Waveform Design," in IEEE Open Journal of the Communications Society, vol. 3, pp. 1643-1655, 2022, doi: 10.1109/OJCOMS.2022.3209641.
一、研究背景与动机
1.1 无线通信技术的演进
无线通信技术从1G演进到5G,经历了显著的技术创新。在早期阶段,受限于硬件能力和理论基础,信号仅能在低频载波上以窄带宽传输。随着技术进步,如今信号可在毫米波(mmWave)频段传输,工作频率可达60 GHz甚至更高;太赫兹(THz)频段的研究也在积极推进中,信号带宽已可达到GHz量级。
在天线技术方面,通信系统从单天线发展到支持数百根天线的大规模MIMO阵列。大规模MIMO技术通过空间复用显著提升了系统容量和频谱效率,成为5G及未来通信系统的关键使能技术。
在波形设计方面,不同代际的通信系统采用了不同的多址和调制方案:3G系统采用码分多址(CDMA)技术;4G/5G系统则主要采用正交频分复用(OFDM)和单载波频分多址(SC-FDMA)技术。面向6G,研究人员正在探索多种先进波形候选方案,包括频谱效率频分复用(SEFDM)、超奈奎斯特(FTN)信令、正交时频空间(OTFS)调制、广义频分复用(GFDM)和滤波器组多载波(FBMC)等。这些新型波形旨在进一步提升频谱效率、降低时延或增强对高移动性场景的适应能力。
1.2 雷达感知技术的发展
传统传感器包括加速度计、陀螺仪、光线传感器、温度传感器以及音视频采集设备等。由于无线信号的无处不在特性,基于射频(RF)的非侵入式、非接触式雷达感知正成为研究热点。
Google开发的"Soli"系统是一个工作在60 GHz的毫米波雷达感知系统,能够感知和理解手指细微动作。通过测量微多普勒特征,雷达和声纳设备可以检测不同类型的人体运动。调频连续波(FMCW)雷达与摄像头的联合检测系统可实现物体检测和三维估计。超宽带(UWB) MIMO雷达配合Vivaldi天线可实现穿墙目标检测。
同时基于WiFi信号的人体活动感知也取得了重要进展。IEEE 802.11bf标准工作组正在制定利用现有WiFi信号实现感知功能的标准。WiFi感知主要有两种方法:接收信号强度指示(RSSI)和信道状态信息(CSI)。虽然RSSI在人体活动检测中取得了成功,但其粗糙的感知分辨率和对噪声的高敏感性限制了进一步应用。CSI方法通过提取幅度和相位信息,可以更好地辅助人体活动检测。代表性工作包括:WiFall系统通过测量CSI"看见"人体活动;WiHear系统通过检测嘴部运动的无线反射来"听见"人类说话;以及利用WiFi信号监测睡眠期间的生命体征和姿势等。
1.3 通感一体化的必要性
传统雷达信号最初并非为通信设计,反之通信信令也不具备固有的感知功能。为实现联合感知与通信,通信无线信号和雷达感知信号必须通过时分复用(TDM)、频分复用(FDM)或空分复用(SDM)模式进行管理。然而,这种复用策略不可避免地造成时间、频率或空间资源的浪费。
而近年来涌现了多种旨在设计和测试适用于通感一体化(ISAC)信令的方法。文献A提出利用LTE帧中的主同步信号(PSS)进行雷达感知;文献B提出了一种空分多址(SDMA)方案,使用相同的发射硬件、相同的时序和频谱占用支持雷达和通信功能,其原理是在彼此的零空间发送空间正交波束以避免干扰;文献C研究了ISAC中的新波形设计,原理是在频域将低带外功率发射信号与雷达信号复用,但这仍是频率复用方案而非真正的双功能设计。
1.4 本文的主要贡献
本文的核心贡献在于首次设计并进行空口(over-the-air)测试,验证了联合双功能雷达通信波形在集成雷达感知和多用户MIMO-OFDM通信系统中的可行性。与现有工作相比,本文的原型测试平台能够使用相同的时间、频率和空间资源同时实现雷达和通信功能。
与纯理论仿真不同,本工作具有以下特点:(1)基于OFDM信号波形设计双功能ISAC实验,使得ISAC框架可直接部署到许多标准通信系统中;(2)通过对通信星座图、误码率(BER)、误差矢量幅度(EVM)和雷达波束图质量的综合实验,获得了在实际中可行的雷达通信权衡因子。
二、通信系统模型
2.1 多用户MIMO-OFDM信号模型
本文考虑多用户MIMO-OFDM传输场景。在这一场景中,基站配备 N N N根发射天线,同时服务 K K K个单天线用户。接收信号的基本表达式为:
Y = H X ~ + W \mathbf{Y} = \mathbf{H}\tilde{\mathbf{X}} + \mathbf{W} Y=HX~+W
这一表达式中各符号的物理含义如下:信道矩阵 H = [ h 1 , h 2 , . . . , h N ] ∈ C K × N \mathbf{H} = [\mathbf{h}_1, \mathbf{h}_2, ..., \mathbf{h}N] \in \mathbb{C}^{K \times N} H=[h1,h2,...,hN]∈CK×N描述了从 N N N根发射天线到 K K K个接收用户之间的无线传播特性,其中第 ( k , n ) (k,n) (k,n)个元素 h k n h{kn} hkn表示从第 n n n根发射天线到第 k k k个用户的复信道增益。预编码后的传输符号矩阵 X ~ = [ x 1 , x 2 , . . . , x L ] ∈ C N × L \tilde{\mathbf{X}} = [\mathbf{x}_1, \mathbf{x}_2, ..., \mathbf{x}_L] \in \mathbb{C}^{N \times L} X~=[x1,x2,...,xL]∈CN×L包含了 N N N根天线在 L L L个时间样本上的发射信号,其中预编码操作的目的是在发射端预先补偿信道影响并管理多用户干扰。噪声矩阵 W = [ w 1 , w 2 , . . . , w L ] ∈ C K × L \mathbf{W} = [\mathbf{w}_1, \mathbf{w}_2, ..., \mathbf{w}_L] \in \mathbb{C}^{K \times L} W=[w1,w2,...,wL]∈CK×L表示 K K K个用户接收到的加性高斯白噪声(AWGN)。
在传统MIMO-OFDM系统中,每根天线负责传输一个独立的OFDM符号流。为了更清晰地展示多用户干扰的影响,上述信号模型可以改写为:
Y = X + ( H X ~ − X ) ⏟ MUI + W \mathbf{Y} = \mathbf{X} + \underbrace{(\mathbf{H}\tilde{\mathbf{X}} - \mathbf{X})}_{\text{MUI}} + \mathbf{W} Y=X+MUI (HX~−X)+W
这里 X ∈ C K × L \mathbf{X} \in \mathbb{C}^{K \times L} X∈CK×L表示用户端期望接收的多载波符号矩阵,即在理想情况下各用户应该收到的信号。第二项 ( H X ~ − X ) (\mathbf{H}\tilde{\mathbf{X}} - \mathbf{X}) (HX~−X)代表多用户干扰(Multi-User Interference, MUI),它反映了实际接收信号与期望信号之间的偏差。MUI的产生源于多个用户共享相同的时频资源,各用户的信号在空间传播过程中相互叠加。
MUI的总功率可通过Frobenius范数计算:
P M U I = ∥ H X ~ − X ∥ F 2 P_{MUI} = \left\|\mathbf{H}\tilde{\mathbf{X}} - \mathbf{X}\right\|_F^2 PMUI= HX~−X F2
其中Frobenius范数定义为矩阵所有元素绝对值平方和的平方根,即 ∥ A ∥ F = ∑ i , j ∣ a i j ∣ 2 \|\mathbf{A}\|F = \sqrt{\sum{i,j}|a_{ij}|^2} ∥A∥F=∑i,j∣aij∣2 。 P M U I P_{MUI} PMUI的值直接决定了系统的信干噪比(SINR):较大的MUI功率意味着较低的SINR,从而导致较高的误码率和较低的系统吞吐量。因此,为实现高吞吐量通信,预编码设计的核心目标是最小化 P M U I P_{MUI} PMUI。
2.2 OFDM信号的数学表示
OFDM是4G、5G和WiFi标准中广泛采用的多载波信号格式,本文的实验系统也采用这一波形。单个OFDM信号在时域的表达式为:
X k = 1 Q ∑ m = 1 M s m exp ( j 2 π m k Q ) X_k = \frac{1}{\sqrt{Q}} \sum_{m=1}^{M} s_m \exp\left(\frac{j2\pi mk}{Q}\right) Xk=Q 1m=1∑Msmexp(Qj2πmk)
这一表达式本质上是离散傅里叶逆变换(IDFT)的数学形式。其中 X k X_k Xk是第 k k k个时域样本,索引范围为 k = 1 , 2 , . . . , Q k = 1, 2, ..., Q k=1,2,...,Q; M M M是子载波总数,每个子载波承载一个调制符号; Q = ρ M Q = \rho M Q=ρM表示时域样本总数, ρ \rho ρ是过采样因子(当 ρ = 1 \rho = 1 ρ=1时为临界采样);归一化因子 1 Q \frac{1}{\sqrt{Q}} Q 1确保发射功率归一化; s m s_m sm是第 m m m个子载波上的调制符号(如QPSK、16QAM等)。
从信号处理的角度理解,OFDM将高速串行数据流转换为多个低速并行子载波传输。每个子载波占用较窄的带宽,因此经历平坦衰落,大大简化了均衡器设计。子载波之间的正交性由 exp ( j 2 π m k Q ) \exp\left(\frac{j2\pi mk}{Q}\right) exp(Qj2πmk)基函数保证。
将上述表达式转换为更紧凑的矩阵形式:
X = F S X = \mathbf{F}S X=FS
其中 F ∈ C Q × M \mathbf{F} \in \mathbb{C}^{Q \times M} F∈CQ×M是子载波矩阵(本质上是DFT矩阵的共轭转置),其第 ( k , m ) (k,m) (k,m)个元素为 [ F ] k , m = exp ( j 2 π m k Q ) [\mathbf{F}]_{k,m} = \exp\left(\frac{j2\pi mk}{Q}\right) [F]k,m=exp(Qj2πmk); S ∈ C M × 1 S \in \mathbb{C}^{M \times 1} S∈CM×1是包含所有子载波符号的向量。
经过无线信道传输并受到AWGN污染后,接收信号表示为:
Y = F S + Z Y = \mathbf{F}S + Z Y=FS+Z
其中 Y ∈ C Q × 1 Y \in \mathbb{C}^{Q \times 1} Y∈CQ×1表示一个完整的OFDM符号, Z Z Z是噪声向量。对于一个OFDM帧,需要生成多个OFDM符号,总共包含 L L L个时间样本。为支持上述MIMO系统模型,需要 K K K个并行的OFDM信号生成器,从而得到用户端符号矩阵 X ∈ C K × L \mathbf{X} \in \mathbb{C}^{K \times L} X∈CK×L。
三、雷达感知与通信的权衡优化理论
3.1 双功能波形设计的核心思想
实现双功能雷达通信的关键挑战在于:如何设计一个波形,使其既能有效传输通信数据,又能产生所需的雷达波束图用于目标检测或跟踪。本文采用的方法是引入一个权衡因子 γ \gamma γ来平衡通信性能和雷达性能。
设所需的雷达发射信号为 X d \mathbf{X}_d Xd,其设计取决于具体的雷达应用场景。一般而言,MIMO雷达波形设计有两种主要类型:第一种是正交波形,用于生成全向(omnidirectional)波束图,适用于搜索位置未知的目标;第二种是定向(directional)波形,用于生成指向特定方向的波束,适用于跟踪已知位置的目标。
考虑总功率约束,权衡优化问题可表述为:
min X ~ γ ∥ H X ~ − X ∥ F 2 + ( 1 − γ ) ∥ X ~ − X d ∥ F 2 \min_{\tilde{\mathbf{X}}} \quad \gamma\left\|\mathbf{H}\tilde{\mathbf{X}} - \mathbf{X}\right\|_F^2 + (1-\gamma)\left\|\tilde{\mathbf{X}} - \mathbf{X}_d\right\|_F^2 X~minγ HX~−X F2+(1−γ) X~−Xd F2
s.t. 1 L ∥ X ~ ∥ F 2 = P T \text{s.t.} \quad \frac{1}{L}\left\|\tilde{\mathbf{X}}\right\|_F^2 = P_T s.t.L1 X~ F2=PT
这个优化目标函数的设计体现了精妙的工程权衡思想。第一项 ∥ H X ~ − X ∥ F 2 \left\|\mathbf{H}\tilde{\mathbf{X}} - \mathbf{X}\right\|F^2 HX~−X F2正是前文定义的MUI功率 P M U I P{MUI} PMUI,最小化该项可确保良好的通信性能。第二项 ∥ X ~ − X d ∥ F 2 \left\|\tilde{\mathbf{X}} - \mathbf{X}_d\right\|_F^2 X~−Xd F2度量实际发射波形与理想雷达波形之间的偏差,最小化该项可确保良好的雷达波束图质量。
权衡因子 γ ∈ [ 0 , 1 ] \gamma \in [0, 1] γ∈[0,1]控制两个目标之间的相对重要性。当 γ = 1 \gamma = 1 γ=1时,优化目标退化为纯通信优化,完全忽略雷达性能;当 γ = 0 \gamma = 0 γ=0时,优化目标退化为纯雷达优化,完全忽略通信性能。对于 0 < γ < 1 0 < \gamma < 1 0<γ<1的中间值,系统在通信和雷达性能之间取得某种平衡。 γ \gamma γ值越大,通信性能越好但雷达性能越差;反之亦然。
约束条件 1 L ∥ X ~ ∥ F 2 = P T \frac{1}{L}\left\|\tilde{\mathbf{X}}\right\|_F^2 = P_T L1 X~ F2=PT确保发射信号的平均功率等于预设值 P T P_T PT,这是实际系统中功率放大器线性工作范围和监管要求所必需的。
3.2 优化问题的数学变换与求解
为便于求解,首先对目标函数进行数学变换。将两个Frobenius范数项展开并合并为单一范数形式:
γ ∥ H X ~ − X ∥ F 2 + ( 1 − γ ) ∥ X ~ − X d ∥ F 2 \gamma\left\|\mathbf{H}\tilde{\mathbf{X}} - \mathbf{X}\right\|_F^2 + (1-\gamma)\left\|\tilde{\mathbf{X}} - \mathbf{X}_d\right\|_F^2 γ HX~−X F2+(1−γ) X~−Xd F2
利用范数的性质,上式可以改写为:
= ∥ [ γ H T , 1 − γ I N ] T X ~ − [ γ X T , 1 − γ X d T ] T ∥ F 2 = \left\|[\sqrt{\gamma}\mathbf{H}^T, \sqrt{1-\gamma}\mathbf{I}_N]^T\tilde{\mathbf{X}} - [\sqrt{\gamma}\mathbf{X}^T, \sqrt{1-\gamma}\mathbf{X}_d^T]^T\right\|_F^2 = [γ HT,1−γ IN]TX~−[γ XT,1−γ XdT]T F2
这一变换的关键insight是:原本分离的通信项和雷达项可以通过适当的矩阵堆叠合并为一个统一的最小二乘问题。
为简化表达式,定义增广矩阵:
A = [ γ H T , 1 − γ I N ] T ∈ C ( K + N ) × N \mathbf{A} = [\sqrt{\gamma}\mathbf{H}^T, \sqrt{1-\gamma}\mathbf{I}_N]^T \in \mathbb{C}^{(K+N) \times N} A=[γ HT,1−γ IN]T∈C(K+N)×N
B = [ γ X T , 1 − γ X d T ] T ∈ C ( K + N ) × L \mathbf{B} = [\sqrt{\gamma}\mathbf{X}^T, \sqrt{1-\gamma}\mathbf{X}_d^T]^T \in \mathbb{C}^{(K+N) \times L} B=[γ XT,1−γ XdT]T∈C(K+N)×L
矩阵 A \mathbf{A} A的上半部分 γ H T \sqrt{\gamma}\mathbf{H}^T γ HT与通信相关,下半部分 1 − γ I N \sqrt{1-\gamma}\mathbf{I}_N 1−γ IN与雷达相关。类似地,矩阵 B \mathbf{B} B的上半部分包含期望的通信符号,下半部分包含期望的雷达波形。
利用这些定义,原优化问题可以重新表述为标准形式:
min X ~ ∥ A X ~ − B ∥ F 2 \min_{\tilde{\mathbf{X}}} \quad \left\|\mathbf{A}\tilde{\mathbf{X}} - \mathbf{B}\right\|_F^2 X~min AX~−B F2
s.t. ∥ X ~ ∥ F 2 = L P T \text{s.t.} \quad \left\|\tilde{\mathbf{X}}\right\|_F^2 = LP_T s.t. X~ F2=LPT
这是一个带有二次等式约束的最小二乘问题。由于约束是非凸的(等式约束定义的是一个球面而非凸集),整体问题是非凸优化问题。然而,可以证明该问题满足强对偶性条件,因此可以通过求解对偶问题获得全局最优解。
对偶问题的求解通常需要迭代算法,计算复杂度较高。为降低实现复杂度,本文采用一种基于最小二乘法的闭式次优解:
X ~ = L P T ∥ A † B ∥ F A † B \tilde{\mathbf{X}} = \frac{\sqrt{LP_T}}{\|\mathbf{A}^\dagger\mathbf{B}\|_F}\mathbf{A}^\dagger\mathbf{B} X~=∥A†B∥FLPT A†B
其中 ( ⋅ ) † (\cdot)^\dagger (⋅)†表示Moore-Penrose伪逆。这个解的直观理解是:首先忽略功率约束求解无约束最小二乘问题得到 A † B \mathbf{A}^\dagger\mathbf{B} A†B,然后通过缩放因子 L P T ∥ A † B ∥ F \frac{\sqrt{LP_T}}{\|\mathbf{A}^\dagger\mathbf{B}\|_F} ∥A†B∥FLPT 将解投影到功率约束定义的球面上。虽然这不是严格的最优解,但在实际应用中性能接近最优且计算高效。
3.3 权衡因子对系统性能的影响分析
图1:纯通信系统(γ=1)和纯雷达系统(γ=0)的雷达波束图对比
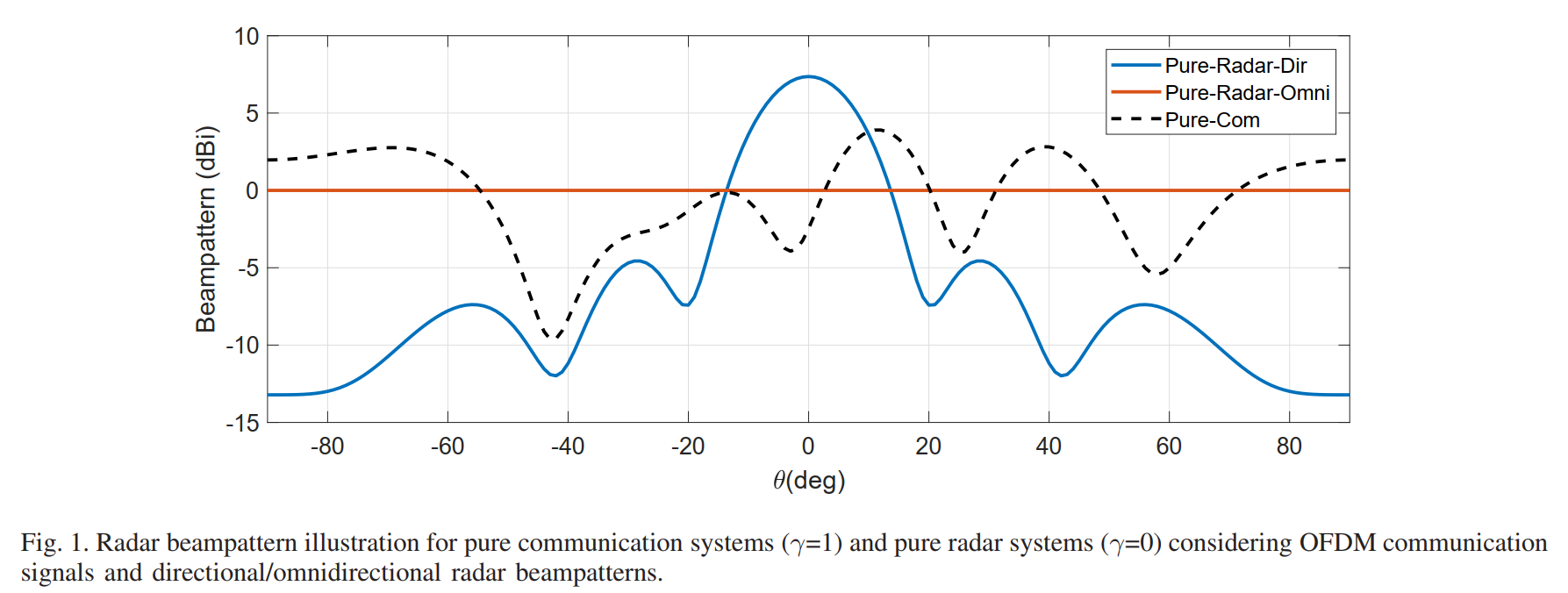
图1展示了在两种极端情况下的雷达波束图特性,横轴为角度θ(单位:度),范围从-80°到+80°,纵轴为波束图增益(单位:dBi)。图中包含三条曲线:
"Pure-Radar-Dir"(纯定向雷达, γ = 0 \gamma=0 γ=0)曲线呈现典型的定向波束图特征。主瓣位于0°方向,增益约为10 dBi,主瓣宽度约为20°。在±40°附近出现第一旁瓣,增益约为2 dBi,主旁瓣比约为8 dB。这种波束图适用于跟踪已知方向的目标,能量集中在目标方向可提高探测距离和精度。
"Pure-Radar-Omni"(纯全向雷达, γ = 0 \gamma=0 γ=0)曲线在整个角度范围内保持相对平坦的增益分布,波动范围约在0至5 dBi之间。这种波束图适用于搜索位置未知的目标,可同时覆盖较大的空间范围。
"Pure-Com"(纯通信, γ = 1 \gamma=1 γ=1)曲线呈现不规则的随机波动形状,在不同角度上的增益变化剧烈,从-15 dBi到接近10 dBi不等。这种随机波束图是纯通信优化的结果------当只关注最小化MUI而完全忽略雷达性能时,发射波形的空间特性不受控制,导致波束图偏离任何理想的雷达模式。
这一对比说明了权衡因子 γ \gamma γ的作用: γ = 0 \gamma=0 γ=0时可获得理想的雷达波束图但通信性能受损; γ = 1 \gamma=1 γ=1时通信性能最优但雷达功能丧失。实际应用中需要选择合适的中间值以同时满足两种功能需求。
四、实验平台设计与配置
4.1 实验平台总体架构
图2:实验平台设置

图2通过三张照片展示了实验平台的实际配置。照片(a)展示了Tx-USRP阵列,这是整个系统的核心发射端,由多个USRP软件无线电设备组成的机架系统。机架上方安装了6根均匀排列的全向天线,形成发射天线阵列。机架内部可以看到多个USRP-RIO-2953R设备,每个设备通过电缆连接到对应的天线。设备前面板显示了各种状态指示灯和连接端口。
照片(b)展示了雷达波束图测量装置(RBMA),这是一个安装在可调节支架上的定向天线系统。照片中可以看到一个对数周期(LP) PCB天线,其后方放置了深色的雷达吸波材料(RAM)用于减少反射。整个装置可以在水平面内旋转,以测量不同角度的接收功率。
照片©展示了两个通信用户(CU-1和CU-2),每个用户由一根全向天线和连接的USRP设备组成。两个用户被放置在不同位置,模拟多用户MIMO场景中的独立接收端。
实验平台构成一个工作在2.4 GHz载波频率的6×2 MIMO-OFDM系统,具体组件配置如下:
发射端USRP阵列(Tx-USRP Array) :作为模拟基站,由六个USRP-RIO-2953R设备组成。每个USRP-RIO-2953R具有两条独立的RF链路,本实验使用其中一条用于信号发射。系统工作参数包括:载波频率 f R F = 2.4 f_{RF} = 2.4 fRF=2.4 GHz,采样率20 MS/s,每个子载波采用QPSK调制,数据子载波数为76,IFFT大小为128,每个OFDM符号包含10个循环前缀(CP)样本用于对抗多径效应。
每个USRP的输出通过Vaunix LPS-402可编程移相器连接到全向天线。在本实验中,移相器仅用作天线支架而未启用相位控制功能,但该功能的激活将为未来研究混合模数多用户MIMO系统提供可能。六根天线以半波长间距( λ / 2 ≈ 6.25 \lambda/2 \approx 6.25 λ/2≈6.25 cm @ 2.4 GHz)排列成均匀线阵(ULA)。第二条RF链路保留用于信号接收,因此该平台最多可支持6×6 MIMO-OFDM系统。
通信用户(CUs) :为简化实验,接收端配置两个用户,构成6×2 MIMO-OFDM下行链路系统。每个用户配备一根全向天线,连接到独立的USRP进行信号采集和处理。
雷达波束图测量装置(RBMA) :由于实验条件限制,整个测试需在室内实验室环境中进行,这给雷达波束图测量带来了挑战------室内空间的多径反射会影响测量精度。为最大程度减轻多径效应并准确测量视距(LOS)信号功率,系统采用6 dBi增益的对数周期(LP) PCB天线,工作频率范围850 MHz至6.5 GHz。LP天线的定向特性有助于聚焦于LOS信号并抑制来自其他方向的多径分量。天线后方放置的雷达吸波材料(RAM)可有效减少1 GHz至40 GHz范围内的信号反射,进一步提高测量精度。RBMA连接到一个独立的USRP用于功率测量。
4.2 实验测量配置详情
图3:实验测量设置
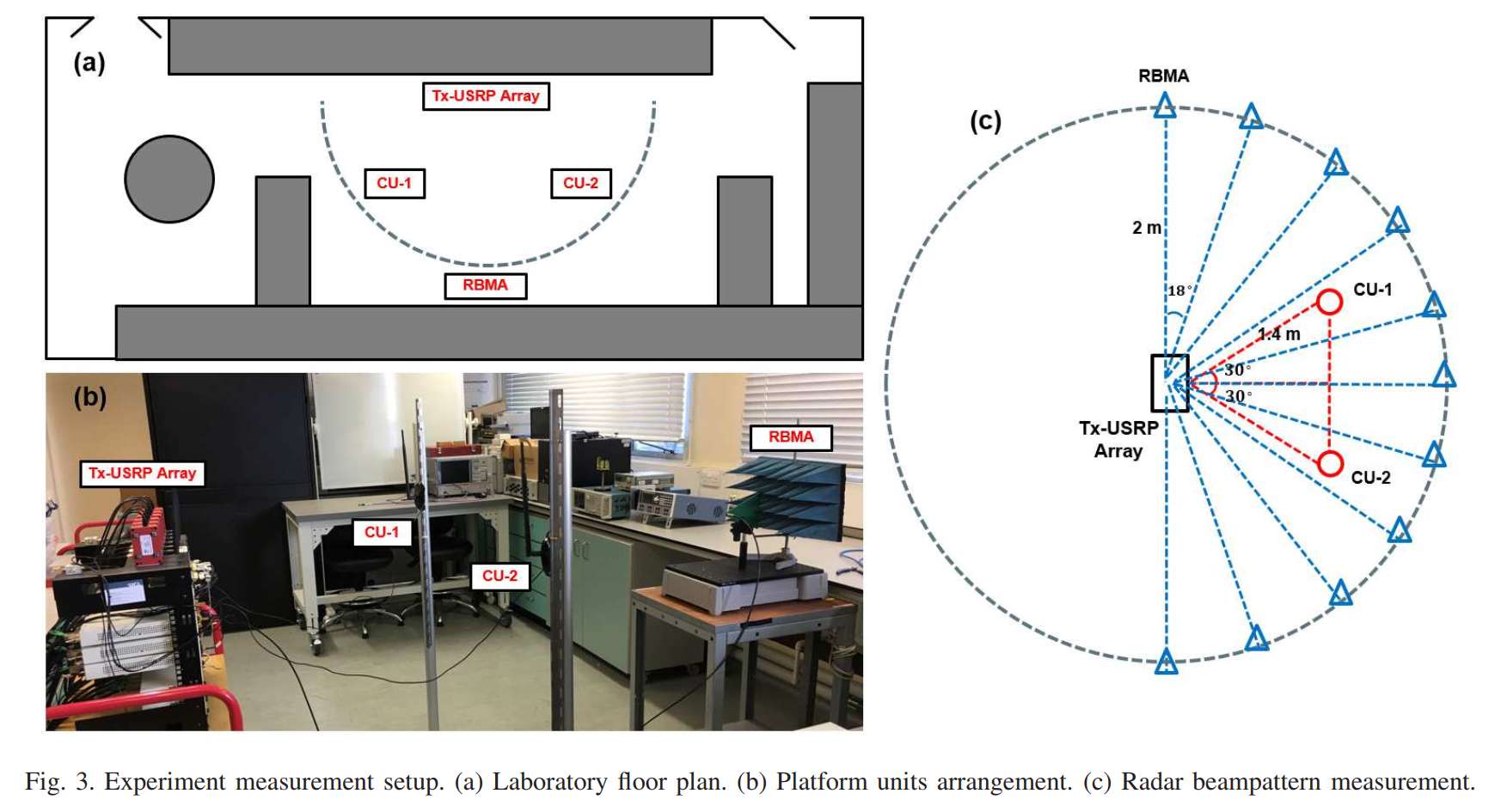
图3通过三个子图详细展示了实验的空间布局和测量方案。
子图(a)是实验室平面图的俯视示意图。实验室空间约4米宽、9米长,呈矩形布局。图中标注了各设备的位置:Tx-USRP Array位于实验室一端,RBMA位于其正前方,CU-1和CU-2分布在两侧。平面图中还用小方块表示了实验室内的各种障碍物(如桌椅、设备柜等),这些物体可能造成信号反射和阻挡。
子图(b)是实验平台的三维透视示意图,更直观地展示了各组件的空间关系。图中可以看到Tx-USRP Array的天线阵列位于较高位置,RBMA的定向天线对准发射阵列,两个通信用户位于不同的水平位置和角度。
子图©专门展示雷达波束图的测量策略。图中显示RBMA以Tx-USRP Array为圆心、2米为半径进行弧形移动测量。测量点分布在180度范围内,每隔18度取一个测量点,共计10个测量位置。CU-1和CU-2位于距离发射阵列1.4米处,两用户之间的水平间距也是1.4米,形成约60度的角度分离。
对于通信部分,室内环境的多径效应不构成根本性障碍,因为无线信道会实时测量,预编码会相应调整以抑制MIMO传输干扰。此外,OFDM信号的多载波结构天然具有对抗多径效应的鲁棒性------循环前缀的引入消除了符号间干扰,而导频符号用于估计各子载波上的信道响应,通过单抽头均衡器即可有效补偿信道影响。
三维空间配置的具体参数为:基站天线阵列高度1.5米,两个用户天线高度同样为1.5米,雷达波束图测量天线高度也设为1.5米以确保与发射阵列处于同一水平面。考虑到2.4 GHz载波对应的波长 λ ≈ 12.5 \lambda \approx 12.5 λ≈12.5 cm,2米的测量距离大于 2 λ 2\lambda 2λ(远场条件通常要求距离大于 2 D 2 / λ 2D^2/\lambda 2D2/λ,其中 D D D为天线孔径),因此可认为测量处于远场区域内。
由于实验室空间有限,难以通过改变传输距离来调节接收SNR。因此实验采用的策略是保持总发射功率不变,通过在接收端添加可控噪声来实现不同SNR条件下的测量。由于各天线的实际SNR存在差异,文中报告的是在用户端测量得到的接收SNR。
雷达波束图功率的计算基于接收到的复符号:
P = 1 Q ∑ k = 1 Q [ ℜ ( X ( k ) ) 2 + ℑ ( X ( k ) ) 2 ] P = \frac{1}{Q}\sum_{k=1}^{Q}[\Re(X(k))^2 + \Im(X(k))^2] P=Q1k=1∑Q[ℜ(X(k))2+ℑ(X(k))2]
其中 X ( k ) X(k) X(k)表示第 k k k个接收复符号, ℜ ( ⋅ ) \Re(\cdot) ℜ(⋅)和 ℑ ( ⋅ ) \Im(\cdot) ℑ(⋅)分别提取复数的实部和虚部, 1 Q \frac{1}{Q} Q1是用于计算平均功率的归一化因子。该公式本质上计算的是接收符号的平均能量,反映了特定角度方向上的接收功率水平。
4.3 帧结构与信道估计方法
图4:双功能雷达通信多用户MIMO系统的帧和资源块结构
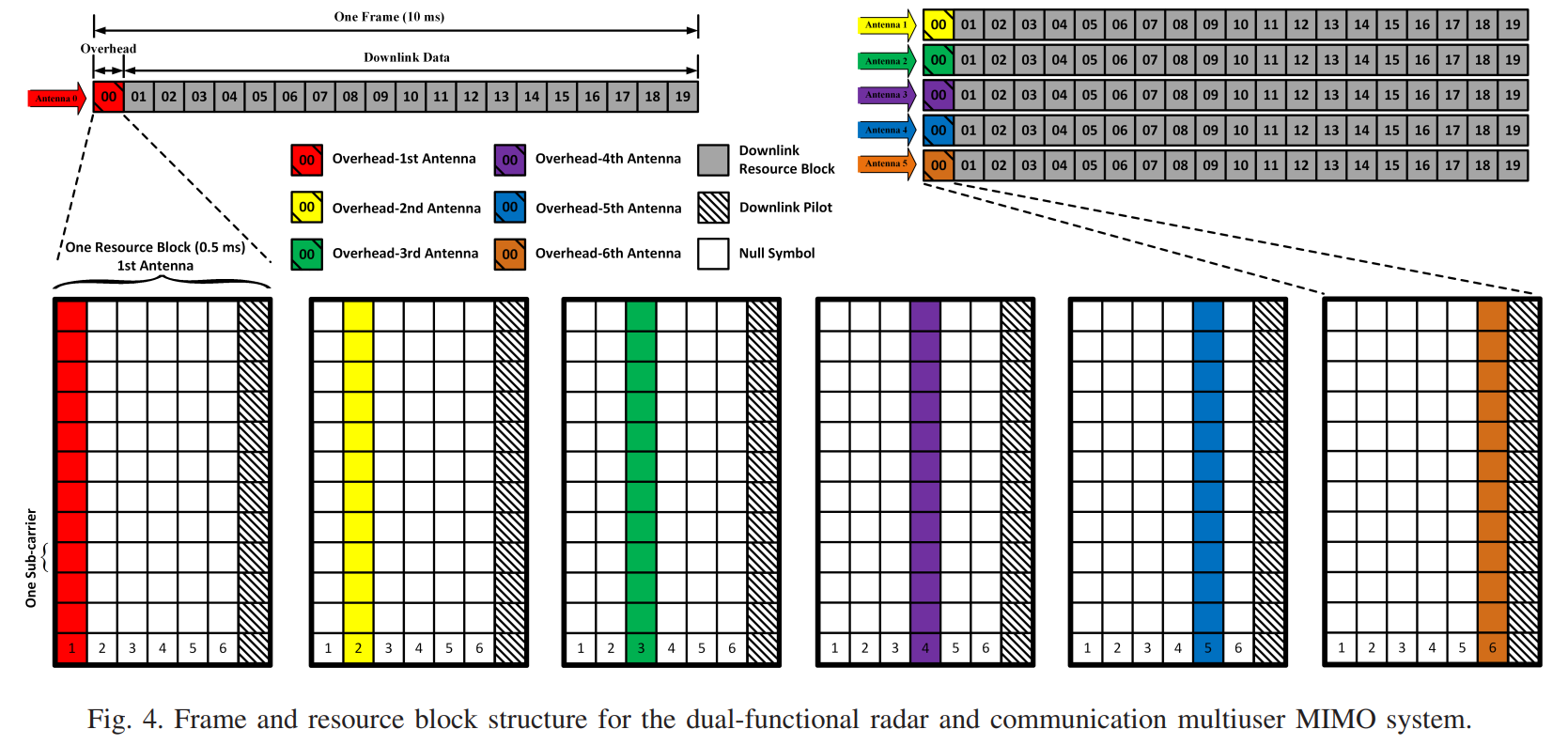
图4展示了系统采用的帧结构设计,这是实现可靠MIMO传输的关键。图的上半部分展示了完整帧结构的时域组织:一帧由20个资源块组成,总时长10 ms(即每个资源块0.5 ms)。资源块编号从00到19,其中资源块00专门用于开销(Overhead),包含MIMO信道估计所需的导频符号;资源块01到19用于下行数据传输。
图的下半部分详细展示了资源块的内部结构。每个资源块包含7个OFDM符号,频域上跨越所有子载波。在开销资源块(00号)中,导频符号在各天线间采用时分复用:第1个OFDM符号位置为第1天线的开销,第2个位置为第2天线的开销,依此类推直到第6天线。这种交织式的导频分配确保了各天线的信道估计不受相互干扰。
图的右侧用颜色编码展示了6根天线在整帧中的资源分配模式。可以看到,在开销资源块中,各天线的导频符号在时域上错开;在数据资源块中,所有天线同时传输数据,并且每个资源块的第一个OFDM符号位置包含下行导频(Downlink Pilot)用于跟踪信道变化。图例说明了不同填充图案的含义:纯色块表示各天线的开销符号,斜线填充表示下行资源块,交叉线填充表示下行导频,空白表示空符号。
MIMO信道估计:基于图4所示的交织开销结构,定义导频矩阵为:
P = [ p 1 0 0 0 0 0 0 p 2 0 0 0 0 0 0 p 3 0 0 0 0 0 0 p 4 0 0 0 0 0 0 p 5 0 0 0 0 0 0 p 6 ] \mathbf{P} = \begin{bmatrix} p_1 & 0 & 0 & 0 & 0 & 0 \\ 0 & p_2 & 0 & 0 & 0 & 0 \\ 0 & 0 & p_3 & 0 & 0 & 0 \\ 0 & 0 & 0 & p_4 & 0 & 0 \\ 0 & 0 & 0 & 0 & p_5 & 0 \\ 0 & 0 & 0 & 0 & 0 & p_6 \end{bmatrix} P= p1000000p2000000p3000000p4000000p5000000p6
这是一个对角矩阵,其中 p 1 , p 2 , . . . , p 6 p_1, p_2, ..., p_6 p1,p2,...,p6分别是六根天线上的导频符号。对角结构确保在任一时刻只有一根天线发射导频,从而实现无干扰的信道测量。
6×2 MIMO系统的信道矩阵表示为:
H = [ h 11 h 12 h 13 h 14 h 15 h 16 h 21 h 22 h 23 h 24 h 25 h 26 ] \mathbf{H} = \begin{bmatrix} h_{11} & h_{12} & h_{13} & h_{14} & h_{15} & h_{16} \\ h_{21} & h_{22} & h_{23} & h_{24} & h_{25} & h_{26} \end{bmatrix} H=[h11h21h12h22h13h23h14h24h15h25h16h26]
其中 h k n h_{kn} hkn表示从第 n n n根发射天线到第 k k k个用户的复信道系数。经过MIMO信道传播和AWGN污染后,接收到的导频符号矩阵为:
y 11 y 12 y 13 y 14 y 15 y 16 y 21 y 22 y 23 y 24 y 25 y 26 \] = H P + \[ z 11 z 21 z 12 z 22 z 13 z 23 z 14 z 24 z 15 z 25 z 16 z 26 \] T \\begin{bmatrix} y_{11} \& y_{12} \& y_{13} \& y_{14} \& y_{15} \& y_{16} \\\\ y_{21} \& y_{22} \& y_{23} \& y_{24} \& y_{25} \& y_{26} \\end{bmatrix} = \\mathbf{H}\\mathbf{P} + \\begin{bmatrix} z_{11} \& z_{21} \\\\ z_{12} \& z_{22} \\\\ z_{13} \& z_{23} \\\\ z_{14} \& z_{24} \\\\ z_{15} \& z_{25} \\\\ z_{16} \& z_{26} \\end{bmatrix}\^T \[y11y21y12y22y13y23y14y24y15y25y16y26\]=HP+ z11z12z13z14z15z16z21z22z23z24z25z26 T 其中 y m , n y_{m,n} ym,n表示第 m m m个用户在第 n n n个时隙接收到的符号, z m , n z_{m,n} zm,n是对应的噪声样本。由于导频矩阵 P \\mathbf{P} P是对角矩阵,在忽略噪声的情况下,MIMO信道矩阵可以通过简单的除法估计: H \^ = \[ y 11 / p 1 y 12 / p 2 y 13 / p 3 y 14 / p 4 y 15 / p 5 y 16 / p 6 y 21 / p 1 y 22 / p 2 y 23 / p 3 y 24 / p 4 y 25 / p 5 y 26 / p 6 \] \\hat{\\mathbf{H}} = \\begin{bmatrix} y_{11}/p_1 \& y_{12}/p_2 \& y_{13}/p_3 \& y_{14}/p_4 \& y_{15}/p_5 \& y_{16}/p_6 \\\\ y_{21}/p_1 \& y_{22}/p_2 \& y_{23}/p_3 \& y_{24}/p_4 \& y_{25}/p_5 \& y_{26}/p_6 \\end{bmatrix} H\^=\[y11/p1y21/p1y12/p2y22/p2y13/p3y23/p3y14/p4y24/p4y15/p5y25/p5y16/p6y26/p6
这种估计方法的优点是计算简单、实现高效,代价是需要占用6个OFDM符号周期用于导频传输。估计得到的信道矩阵 H ^ \hat{\mathbf{H}} H^将用于发射端的预编码设计,以抑制多用户干扰。
OFDM信道估计:除了MIMO空间信道外,还需要估计频率选择性信道以补偿多径效应。多载波信号的一个重要特性是:通过傅里叶变换,时域的卷积(多径信道的效应)被转换为频域的逐点乘法。这意味着频率选择性信道可以等效为一个对角矩阵。
定义多径信道矩阵 G \mathbf{G} G,考虑多径效应的接收信号表示为:
Y = G F p g + Z Y = \mathbf{G}\mathbf{F}p_g + Z Y=GFpg+Z
其中 p g p_g pg是图4中定义的下行导频符号。在接收端进行FFT解调后,信号变为:
R g = F ∗ G F p g + F ∗ Z = D p g + W R_g = \mathbf{F}^*\mathbf{G}\mathbf{F}p_g + \mathbf{F}^*Z = \mathbf{D}p_g + W Rg=F∗GFpg+F∗Z=Dpg+W
其中 D = F ∗ G F \mathbf{D} = \mathbf{F}^*\mathbf{G}\mathbf{F} D=F∗GF是一个对角矩阵。这个对角化是OFDM系统的核心优势所在------无论原始多径信道 G \mathbf{G} G多么复杂,经过傅里叶变换后都变成了简单的对角形式。对角矩阵 D \mathbf{D} D的第 m m m个对角元素 d m d_m dm表示第 m m m个子载波上的复信道增益。
通过提取 diag ( D ) \text{diag}(\mathbf{D}) diag(D),可以实现单抽头均衡:每个子载波上的接收符号只需除以对应的信道系数即可恢复原始发射符号。这种均衡方式可以有效消除多径效应、不完美定时同步、载波相位偏移和功率失真等影响。
五、实验结果与性能分析
5.1 全向波束系统的测量结果
图5:全向系统的用户端星座图和发射端雷达波束图测量结果
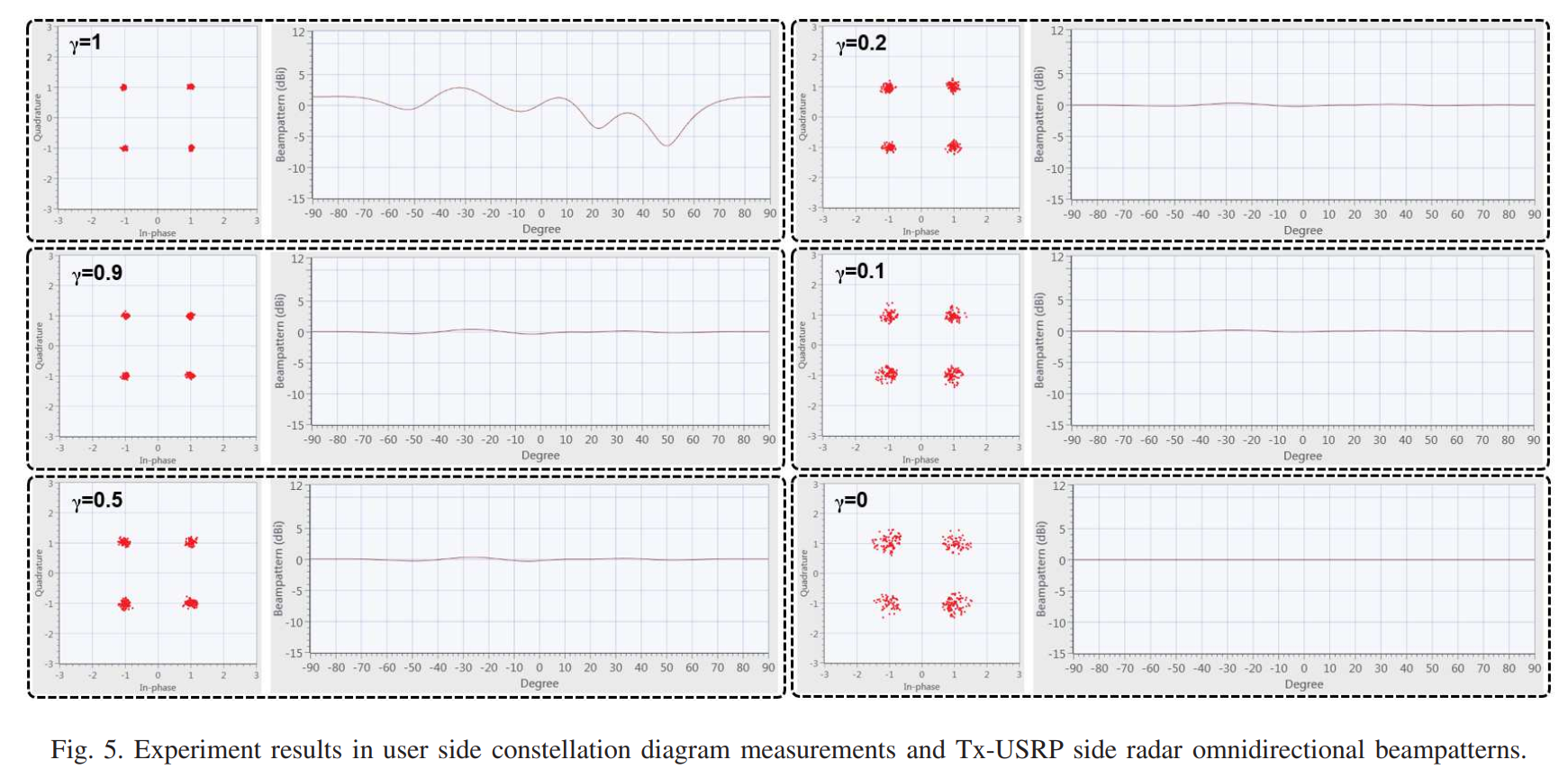
图5是本文最重要的实验结果之一,展示了在六个不同 γ \gamma γ值(1, 0.9, 0.5, 0.2, 0.1, 0)下全向RadarCom系统的性能。每个 γ \gamma γ值对应图中的一个子图,子图左侧是接收端的QPSK星座图,右侧是发射端的雷达波束图。
当 γ = 1 \gamma = 1 γ=1(纯通信模式)时,左侧星座图显示四个QPSK星座点清晰分离、紧密聚集,表明通信性能优异。星座点位于复平面的四个象限中心附近,相位分别约为45°、135°、225°和315°。右侧波束图呈现不规则形状,在-90°到+90°范围内增益波动剧烈,完全偏离理想的全向特性。
当 γ = 0.9 \gamma = 0.9 γ=0.9时,星座图仍然保持良好的四簇分离特性,虽然各簇内的点分布略有扩散,但仍可正确判决。波束图开始呈现接近平坦的全向特性,在大部分角度上增益稳定在0至5 dBi范围内。这表明 γ = 0.9 \gamma = 0.9 γ=0.9可能是一个较好的工作点,既保证了通信质量,又获得了合理的雷达波束图。
当 γ = 0.5 \gamma = 0.5 γ=0.5时,星座点开始出现明显扩散,四个簇之间的边界变得模糊,但仍可辨识。波束图进一步改善,更加接近理想的全向形状。
当 γ = 0.2 \gamma = 0.2 γ=0.2时,星座点严重扩散,部分点开始跨越判决边界,误码率将显著上升。波束图已经非常接近理想全向特性。
当 γ = 0.1 \gamma = 0.1 γ=0.1时,星座点极度分散,四个簇已难以区分,同时出现了相位旋转现象(整体星座图似乎发生了角度偏移)。通信功能严重退化。波束图质量优秀。
当 γ = 0 \gamma = 0 γ=0(纯雷达模式)时,星座点完全散开,呈现近似均匀分布的随机特性,通信功能完全丧失。波束图达到理想的全向状态,在整个角度范围内增益变化最小。
从图5可以得出重要结论:对于全向RadarCom系统, γ = 0.9 \gamma = 0.9 γ=0.9是一个较优的工程选择,它在保证通信星座图质量(从而保证低误码率)的同时,获得了接近理想的全向雷达波束图。
5.2 定向波束系统的测量结果
图6:定向系统的用户端星座图和发射端雷达波束图测量结果
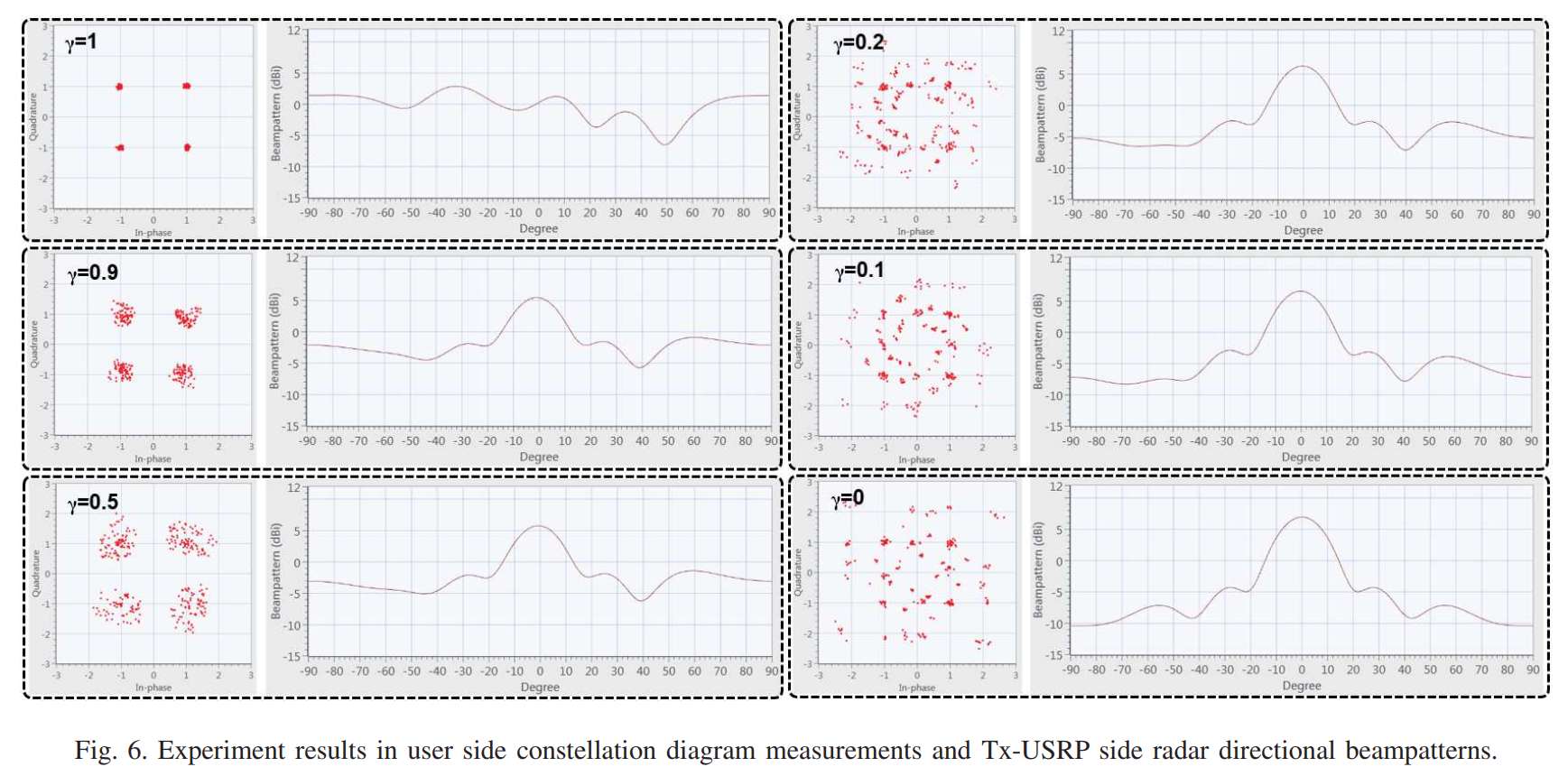
图6采用与图5相同的布局,展示了定向RadarCom系统在相同六个 γ \gamma γ值下的性能。定向系统的目标是在保证通信性能的同时,产生指向特定方向(本例中为0°)的雷达波束。
当 γ = 1 \gamma = 1 γ=1(纯通信模式)时,星座图与图5中相同(因为纯通信模式不区分全向或定向),四个QPSK星座点清晰分离。波束图同样呈现随机不规则形状,没有定向特性。
当 γ = 0.9 \gamma = 0.9 γ=0.9时,星座图保持良好的四簇分离。波束图开始呈现定向特性:在0°方向出现明显的主瓣,增益约为8-10 dBi;在±60°附近出现旁瓣,增益约为2-4 dBi;主旁瓣比(PSLR)约为6 dB。这是一个具有实用价值的雷达波束图。
当 γ = 0.5 \gamma = 0.5 γ=0.5时,星座点出现显著扩散和相位旋转,但四个簇仍可大致辨识。波束图的定向特性更加明显,主瓣更窄更尖锐。
当 γ = 0.2 \gamma = 0.2 γ=0.2、 0.1 0.1 0.1和 0 0 0时,星座点严重退化,呈现大幅度的散射和旋转。通信功能基本丧失。与此同时,雷达波束图达到近乎理想的定向状态,主瓣清晰、旁瓣低矮。
与全向系统相比,定向系统的权衡特性更为陡峭: γ \gamma γ从1减小到0.9时,波束图改善显著,但星座图质量下降也更为明显。这可能是因为定向波束图对波形施加了更严格的约束,与通信优化目标的冲突更加尖锐。
图6的结论与图5一致: γ = 0.9 \gamma = 0.9 γ=0.9是定向RadarCom系统的推荐工作点,能够在可接受的通信性能损失下获得有效的定向雷达波束图。
5.3 实测雷达波束图分析
图7:RBMA测量的全向和定向雷达波束图( γ = 0.9 , 0.5 , 0 \gamma = 0.9, 0.5, 0 γ=0.9,0.5,0)
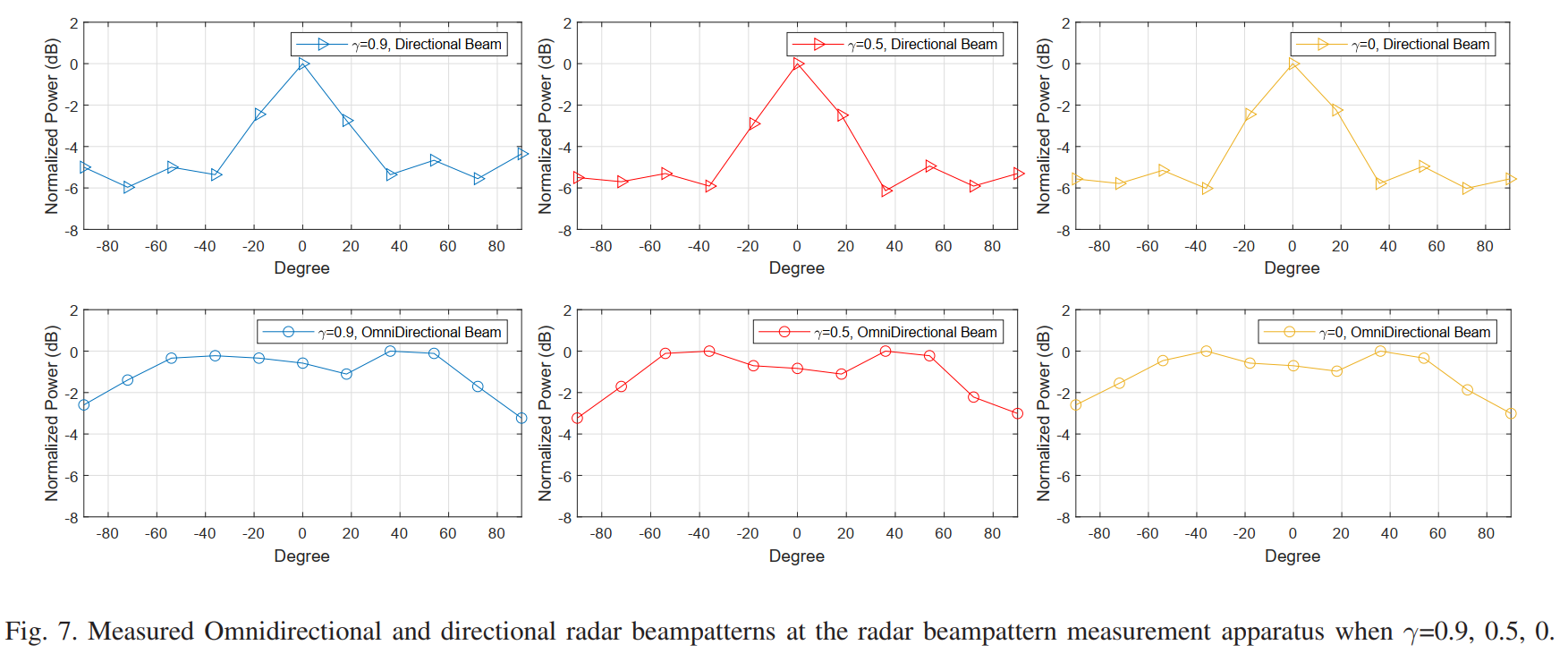
图7展示了通过雷达波束图测量装置(RBMA)实际测量得到的波束图,共包含6个子图,分别对应定向和全向系统在三个 γ \gamma γ值下的结果。所有子图的横轴为角度(-80°到+80°),纵轴为归一化功率(dB)。
对于定向波束系统(上排三个子图):
γ = 0.9 \gamma = 0.9 γ=0.9时的实测定向波束图在0°方向呈现清晰的主瓣,归一化功率约为0 dB(最大值)。主瓣宽度约为30-40°。在±60°附近观察到旁瓣,功率约为-4 dB。实测主旁瓣比约为4 dB,略低于图6中基于信道矩阵计算的理论值(约6 dB),这一差异主要由测量环境中的多径效应和测量误差引起。
γ = 0.5 \gamma = 0.5 γ=0.5时的定向波束图显示更尖锐的主瓣和更低的旁瓣水平,整体波束图质量优于 γ = 0.9 \gamma = 0.9 γ=0.9的情况。
γ = 0 \gamma = 0 γ=0时的定向波束图达到最佳形态,主瓣最窄、旁瓣最低,与理想定向波束图最为接近。
对于全向波束系统(下排三个子图):
γ = 0.9 \gamma = 0.9 γ=0.9时的实测全向波束图在大部分角度范围内功率波动约在±2 dB以内,但并非完全平坦。在某些角度(如-40°附近)观察到约3 dB的凹陷,这可能是由测量环境的特定反射路径造成的。
γ = 0.5 \gamma = 0.5 γ=0.5时的全向波束图平坦度有所改善,角度间的功率差异减小。
γ = 0 \gamma = 0 γ=0时的全向波束图最为平坦,但仍存在约2 dB的波动,未能达到图5中理论计算的完美平坦状态。这再次说明了实际测量环境与理想条件之间的差距。
图7的重要价值在于验证了双功能波形设计的实际可行性:即使在非理想的室内测量环境中,通过适当选择权衡因子 γ \gamma γ,仍然可以获得具有实用价值的雷达波束图。
5.4 误差矢量幅度(EVM)性能分析
图8:全向和定向RadarCom系统的EVM与γ的关系曲线
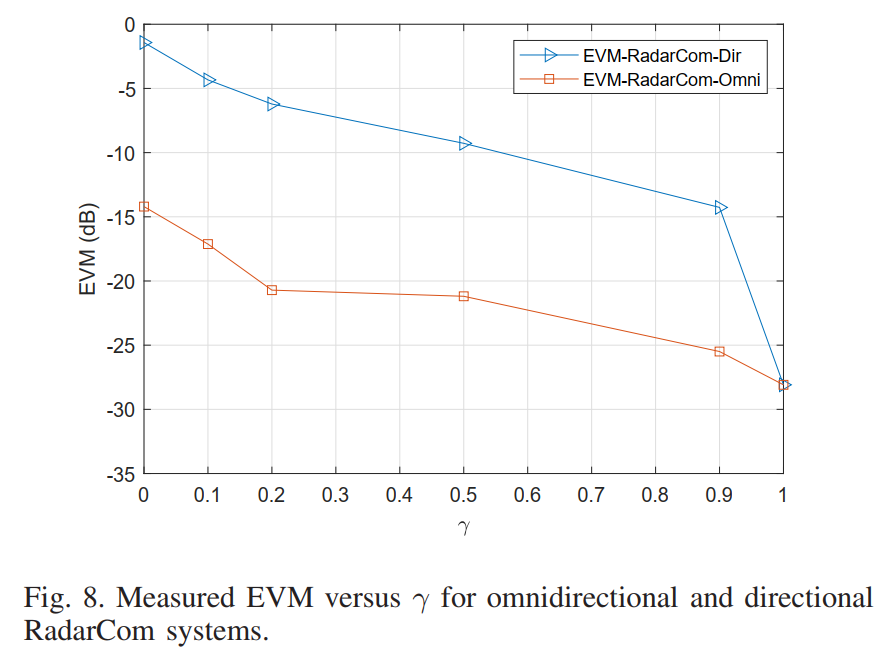
图8定量比较了两种系统在不同 γ \gamma γ值下的通信性能。横轴为权衡因子 γ \gamma γ(0到1),纵轴为EVM(dB)。EVM是衡量调制质量的重要指标,定义为实际接收星座点与理想位置之间偏差的均方根值与理想幅度的比值。较低(更负)的EVM值表示更好的调制质量。
图中包含两条曲线:"EVM-RadarCom-Omni"(全向系统,蓝色圆点标记)和"EVM-RadarCom-Dir"(定向系统,红色叉号标记)。
两条曲线都显示EVM随 γ \gamma γ增大而改善(数值更负)的总体趋势,这符合预期------更大的 γ \gamma γ值意味着更侧重通信优化。
全向系统的EVM曲线变化相对平缓。当 γ \gamma γ从0增加到0.9时,EVM从约-5 dB改善到约-25 dB;从0.9增加到1时,进一步改善到约-30 dB。曲线在 γ = 0.5 \gamma = 0.5 γ=0.5到 γ = 1 \gamma = 1 γ=1区间内近似线性。
定向系统的EVM曲线变化更为陡峭,特别是在高 γ \gamma γ值区域。当 γ \gamma γ从0增加到0.5时,EVM从约-2 dB改善到约-10 dB;从0.5增加到0.9时,改善到约-20 dB;从0.9增加到1时,急剧改善到约-33 dB。曲线在 γ = 0.9 \gamma = 0.9 γ=0.9到 γ = 1 \gamma = 1 γ=1区间显示出明显的非线性特性。
在所有 γ \gamma γ值下,全向系统的EVM性能均优于定向系统。这一差异在 γ = 0.5 \gamma = 0.5 γ=0.5附近最为显著(约10 dB差距),在 γ = 1 \gamma = 1 γ=1时差距最小(约3 dB)。
图8提供了定量依据来选择工作点:如果应用场景对EVM有特定要求(如-20 dB),则全向系统可选择 γ ≈ 0.8 \gamma \approx 0.8 γ≈0.8,而定向系统需要 γ ≈ 0.95 \gamma \approx 0.95 γ≈0.95。这说明定向系统需要更高的 γ \gamma γ值才能达到与全向系统相当的通信质量。
5.5 误码率(BER)性能测量
图9:全向系统在不同γ值下的BER与SNR关系曲线
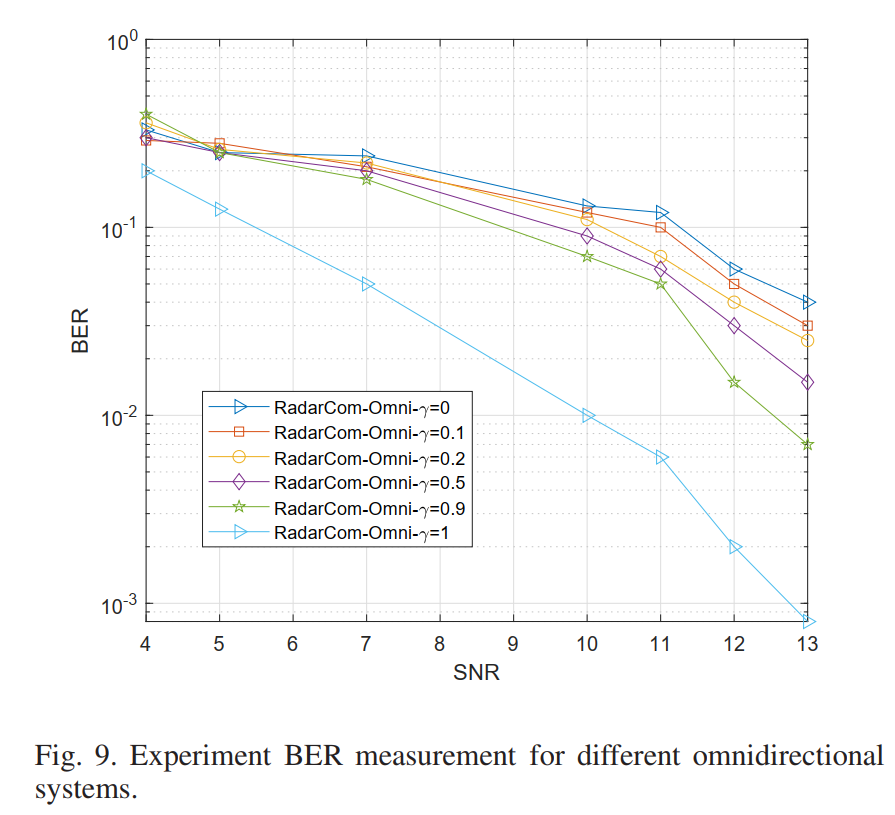
图9展示了全向RadarCom系统的误码率性能,是评估通信可靠性的核心指标。横轴为信噪比SNR(4到13 dB),纵轴为误码率BER(对数坐标, 1 0 − 3 10^{-3} 10−3到 1 0 0 10^0 100)。图中包含六条曲线,分别对应 γ = 0 , 0.1 , 0.2 , 0.5 , 0.9 , 1 \gamma = 0, 0.1, 0.2, 0.5, 0.9, 1 γ=0,0.1,0.2,0.5,0.9,1。
γ = 1 \gamma = 1 γ=1(纯通信)曲线位于最右侧,表现出最好的BER性能。在SNR = 6 dB时BER约为 1 0 − 1 10^{-1} 10−1,在SNR = 10 dB时BER降至约 1 0 − 2 10^{-2} 10−2,在SNR = 13 dB时BER接近 1 0 − 3 10^{-3} 10−3。曲线斜率表明系统正常工作在AWGN信道的瀑布区。
γ = 0.9 \gamma = 0.9 γ=0.9曲线与 γ = 1 \gamma = 1 γ=1曲线大致平行,但向右偏移约2-3 dB。这意味着在相同BER目标下, γ = 0.9 \gamma = 0.9 γ=0.9系统需要额外2-3 dB的SNR作为代价来换取雷达功能。考虑到该SNR损失换来了有效的全向雷达波束图(如图5和图7所示),这是一个合理的工程权衡。
γ = 0.5 \gamma = 0.5 γ=0.5曲线进一步右移,与 γ = 1 \gamma = 1 γ=1的差距扩大到约5-6 dB。
γ = 0.2 \gamma = 0.2 γ=0.2和 γ = 0.1 \gamma = 0.1 γ=0.1曲线显示更大的性能损失,BER在测量的SNR范围内始终较高。
γ = 0 \gamma = 0 γ=0(纯雷达)曲线位于最左侧但表现最差,BER几乎不随SNR改善,在整个测量范围内保持在 1 0 − 1 10^{-1} 10−1附近。这印证了图5中的观察:当 γ = 0 \gamma = 0 γ=0时,星座点完全散开,通信功能丧失。
图9的结果支持选择 γ = 0.9 \gamma = 0.9 γ=0.9作为全向系统的工作点:相对于纯通信系统仅损失2-3 dB的SNR,即可实现双功能操作。
图10:定向系统在不同γ值下的BER与SNR关系曲线
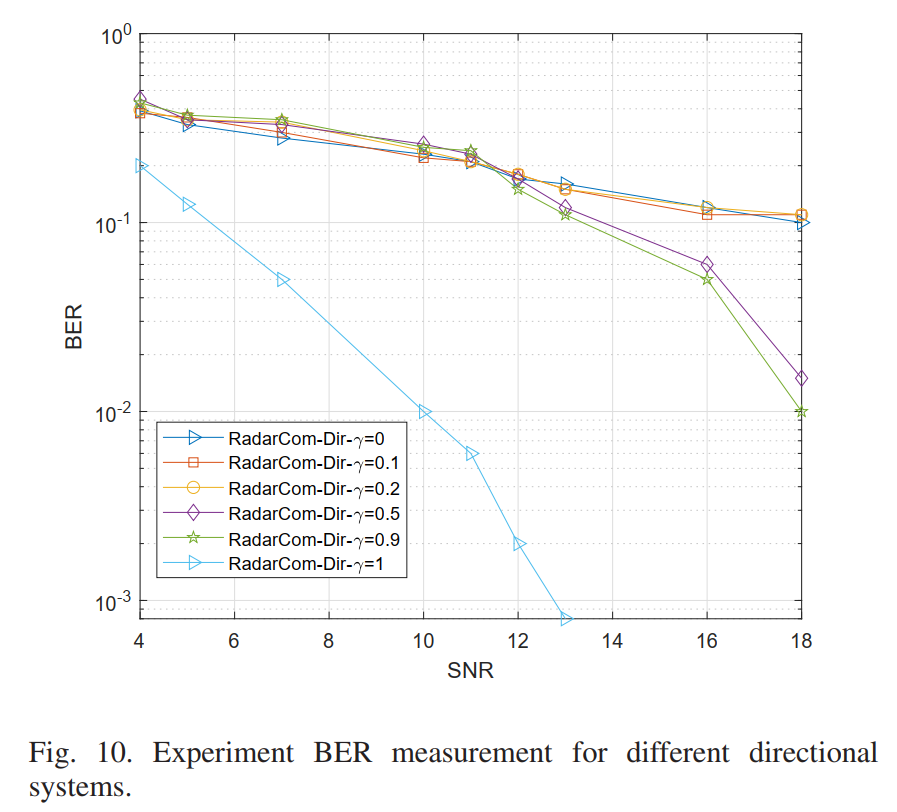
图10展示了定向RadarCom系统的BER性能,格式与图9相同,但SNR范围扩展到4-18 dB以适应定向系统更大的性能差异。
γ = 1 \gamma = 1 γ=1(纯通信)曲线仍然表现最好,性能与图9中的全向系统相当。
γ = 0.9 \gamma = 0.9 γ=0.9曲线与 γ = 1 \gamma = 1 γ=1的差距显著扩大到约8 dB,远大于全向系统中观察到的2-3 dB。例如,要达到BER = 1 0 − 2 10^{-2} 10−2, γ = 1 \gamma = 1 γ=1需要约11 dB SNR,而 γ = 0.9 \gamma = 0.9 γ=0.9需要约19 dB SNR。这一巨大差距与图6和图8中的观察一致:定向波束图约束对通信性能的影响比全向波束图更为严重。
γ = 0.5 , 0.2 , 0.1 , 0 \gamma = 0.5, 0.2, 0.1, 0 γ=0.5,0.2,0.1,0的曲线依次右移,性能逐渐恶化。 γ = 0 \gamma = 0 γ=0时的BER在整个SNR范围内基本保持在 1 0 − 1 10^{-1} 10−1以上,与图9类似。
图10揭示了定向RadarCom系统设计的核心挑战:定向波束图的约束与通信优化目标之间存在更尖锐的冲突,导致更大的性能权衡代价。在实际应用中,如果定向雷达功能是必需的,则需要预留更大的SNR裕量或采用更强的信道编码来补偿这一损失。
六、结论与展望
本文设计了一个空口多用户MIMO-OFDM测试平台,首次在实验中验证了双功能雷达感知与通信波形的可行性。研究的主要发现包括:
在理论层面,通过引入权衡因子 γ \gamma γ的优化框架,将通信与雷达的双重目标统一到单一数学问题中。闭式次优解 X ~ = L P T ∥ A † B ∥ F A † B \tilde{\mathbf{X}} = \frac{\sqrt{LP_T}}{\|\mathbf{A}^\dagger\mathbf{B}\|_F}\mathbf{A}^\dagger\mathbf{B} X~=∥A†B∥FLPT A†B提供了计算高效的波形设计方法。
在实验层面,空口测试揭示了 γ = 0.9 \gamma = 0.9 γ=0.9作为最优权衡因子的实用价值。对于全向系统,该工作点在保持清晰星座图的同时获得了合理的全向波束图,BER性能损失约2-3 dB。对于定向系统,虽然BER损失增大到约8 dB,但仍可获得主旁瓣比约6 dB的定向波束图。
实测雷达波束图与仿真结果具有合理的一致性,验证了双功能波形设计在实际环境中的有效性。实测结果表明,即使在多径丰富的室内环境中,适当设计的RadarCom波形仍能产生可用的雷达波束图。
附录:数学推导补充
A.1 多用户干扰功率的Frobenius范数展开
对于MUI功率表达式 P M U I = ∥ H X ~ − X ∥ F 2 P_{MUI} = \left\|\mathbf{H}\tilde{\mathbf{X}} - \mathbf{X}\right\|_F^2 PMUI= HX~−X F2,根据Frobenius范数的定义:
∥ A ∥ F 2 = tr ( A H A ) = ∑ i , j ∣ a i j ∣ 2 \left\|\mathbf{A}\right\|F^2 = \text{tr}(\mathbf{A}^H\mathbf{A}) = \sum{i,j}|a_{ij}|^2 ∥A∥F2=tr(AHA)=i,j∑∣aij∣2
其中 tr ( ⋅ ) \text{tr}(\cdot) tr(⋅)表示矩阵的迹, ( ⋅ ) H (\cdot)^H (⋅)H表示共轭转置。因此:
P M U I = tr [ ( H X ~ − X ) H ( H X ~ − X ) ] P_{MUI} = \text{tr}\left[(\mathbf{H}\tilde{\mathbf{X}} - \mathbf{X})^H(\mathbf{H}\tilde{\mathbf{X}} - \mathbf{X})\right] PMUI=tr[(HX~−X)H(HX~−X)]
展开得:
P M U I = tr [ X ~ H H H H X ~ − X ~ H H H X − X H H X ~ + X H X ] P_{MUI} = \text{tr}\left[\tilde{\mathbf{X}}^H\mathbf{H}^H\mathbf{H}\tilde{\mathbf{X}} - \tilde{\mathbf{X}}^H\mathbf{H}^H\mathbf{X} - \mathbf{X}^H\mathbf{H}\tilde{\mathbf{X}} + \mathbf{X}^H\mathbf{X}\right] PMUI=tr[X~HHHHX~−X~HHHX−XHHX~+XHX]
= tr ( X ~ H H H H X ~ ) − 2 ℜ { tr ( X H H X ~ ) } + tr ( X H X ) = \text{tr}(\tilde{\mathbf{X}}^H\mathbf{H}^H\mathbf{H}\tilde{\mathbf{X}}) - 2\Re\{\text{tr}(\mathbf{X}^H\mathbf{H}\tilde{\mathbf{X}})\} + \text{tr}(\mathbf{X}^H\mathbf{X}) =tr(X~HHHHX~)−2ℜ{tr(XHHX~)}+tr(XHX)
这说明 P M U I P_{MUI} PMUI是关于 X ~ \tilde{\mathbf{X}} X~的二次函数,可通过令梯度为零找到无约束最优解。
A.2 优化目标的矩阵堆叠变换推导
原始优化目标为:
J ( X ~ ) = γ ∥ H X ~ − X ∥ F 2 + ( 1 − γ ) ∥ X ~ − X d ∥ F 2 J(\tilde{\mathbf{X}}) = \gamma\left\|\mathbf{H}\tilde{\mathbf{X}} - \mathbf{X}\right\|_F^2 + (1-\gamma)\left\|\tilde{\mathbf{X}} - \mathbf{X}_d\right\|_F^2 J(X~)=γ HX~−X F2+(1−γ) X~−Xd F2
利用Frobenius范数的缩放性质 ∥ c A ∥ F = ∣ c ∣ ∥ A ∥ F \|c\mathbf{A}\|_F = |c|\|\mathbf{A}\|_F ∥cA∥F=∣c∣∥A∥F,有:
γ ∥ H X ~ − X ∥ F 2 = ∥ γ ( H X ~ − X ) ∥ F 2 = ∥ γ H X ~ − γ X ∥ F 2 \gamma\left\|\mathbf{H}\tilde{\mathbf{X}} - \mathbf{X}\right\|_F^2 = \left\|\sqrt{\gamma}(\mathbf{H}\tilde{\mathbf{X}} - \mathbf{X})\right\|_F^2 = \left\|\sqrt{\gamma}\mathbf{H}\tilde{\mathbf{X}} - \sqrt{\gamma}\mathbf{X}\right\|_F^2 γ HX~−X F2= γ (HX~−X) F2= γ HX~−γ X F2
( 1 − γ ) ∥ X ~ − X d ∥ F 2 = ∥ 1 − γ ( X ~ − X d ) ∥ F 2 = ∥ 1 − γ I N X ~ − 1 − γ X d ∥ F 2 (1-\gamma)\left\|\tilde{\mathbf{X}} - \mathbf{X}_d\right\|_F^2 = \left\|\sqrt{1-\gamma}(\tilde{\mathbf{X}} - \mathbf{X}_d)\right\|_F^2 = \left\|\sqrt{1-\gamma}\mathbf{I}_N\tilde{\mathbf{X}} - \sqrt{1-\gamma}\mathbf{X}_d\right\|_F^2 (1−γ) X~−Xd F2= 1−γ (X~−Xd) F2= 1−γ INX~−1−γ Xd F2
利用分块矩阵的Frobenius范数性质 ∥ [ A B ] ∥ F 2 = ∥ A ∥ F 2 + ∥ B ∥ F 2 \left\|\begin{bmatrix}\mathbf{A}\\\mathbf{B}\end{bmatrix}\right\|_F^2 = \|\mathbf{A}\|_F^2 + \|\mathbf{B}\|_F^2 [AB] F2=∥A∥F2+∥B∥F2,将两项合并:
J ( X ~ ) = ∥ [ γ H 1 − γ I N ] X ~ − [ γ X 1 − γ X d ] ∥ F 2 J(\tilde{\mathbf{X}}) = \left\|\begin{bmatrix}\sqrt{\gamma}\mathbf{H}\\\sqrt{1-\gamma}\mathbf{I}_N\end{bmatrix}\tilde{\mathbf{X}} - \begin{bmatrix}\sqrt{\gamma}\mathbf{X}\\\sqrt{1-\gamma}\mathbf{X}_d\end{bmatrix}\right\|_F^2 J(X~)= [γ H1−γ IN]X~−[γ X1−γ Xd] F2
定义增广矩阵 A = [ γ H 1 − γ I N ] \mathbf{A} = \begin{bmatrix}\sqrt{\gamma}\mathbf{H}\\\sqrt{1-\gamma}\mathbf{I}_N\end{bmatrix} A=[γ H1−γ IN]和 B = [ γ X 1 − γ X d ] \mathbf{B} = \begin{bmatrix}\sqrt{\gamma}\mathbf{X}\\\sqrt{1-\gamma}\mathbf{X}_d\end{bmatrix} B=[γ X1−γ Xd],则:
J ( X ~ ) = ∥ A X ~ − B ∥ F 2 J(\tilde{\mathbf{X}}) = \left\|\mathbf{A}\tilde{\mathbf{X}} - \mathbf{B}\right\|_F^2 J(X~)= AX~−B F2
A.3 无约束最小二乘问题的闭式解
考虑无约束优化问题 min X ~ ∥ A X ~ − B ∥ F 2 \min_{\tilde{\mathbf{X}}} \left\|\mathbf{A}\tilde{\mathbf{X}} - \mathbf{B}\right\|_F^2 minX~ AX~−B F2。
对 X ~ \tilde{\mathbf{X}} X~求梯度并令其为零。利用矩阵求导公式 ∂ ∂ X ∥ A X − B ∥ F 2 = 2 A H ( A X − B ) \frac{\partial}{\partial\mathbf{X}}\|\mathbf{AX}-\mathbf{B}\|_F^2 = 2\mathbf{A}^H(\mathbf{AX}-\mathbf{B}) ∂X∂∥AX−B∥F2=2AH(AX−B),得:
∂ J ∂ X ~ = 2 A H ( A X ~ − B ) = 0 \frac{\partial J}{\partial\tilde{\mathbf{X}}} = 2\mathbf{A}^H(\mathbf{A}\tilde{\mathbf{X}} - \mathbf{B}) = 0 ∂X~∂J=2AH(AX~−B)=0
A H A X ~ = A H B \mathbf{A}^H\mathbf{A}\tilde{\mathbf{X}} = \mathbf{A}^H\mathbf{B} AHAX~=AHB
这是标准的正规方程(normal equation)。若 A H A \mathbf{A}^H\mathbf{A} AHA可逆,则:
X ~ L S = ( A H A ) − 1 A H B = A † B \tilde{\mathbf{X}}_{LS} = (\mathbf{A}^H\mathbf{A})^{-1}\mathbf{A}^H\mathbf{B} = \mathbf{A}^\dagger\mathbf{B} X~LS=(AHA)−1AHB=A†B
其中 A † = ( A H A ) − 1 A H \mathbf{A}^\dagger = (\mathbf{A}^H\mathbf{A})^{-1}\mathbf{A}^H A†=(AHA)−1AH是 A \mathbf{A} A的Moore-Penrose伪逆。
A.4 功率约束的投影
最小二乘解 X ~ L S = A † B \tilde{\mathbf{X}}_{LS} = \mathbf{A}^\dagger\mathbf{B} X~LS=A†B通常不满足功率约束 ∥ X ~ ∥ F 2 = L P T \|\tilde{\mathbf{X}}\|_F^2 = LP_T ∥X~∥F2=LPT。为满足约束,采用投影方法。
设 X ~ = α X ~ L S \tilde{\mathbf{X}} = \alpha\tilde{\mathbf{X}}_{LS} X~=αX~LS,其中 α \alpha α是待定的缩放因子。代入功率约束:
∥ α X ~ L S ∥ F 2 = L P T \|\alpha\tilde{\mathbf{X}}_{LS}\|_F^2 = LP_T ∥αX~LS∥F2=LPT
∣ α ∣ 2 ∥ X ~ L S ∥ F 2 = L P T |\alpha|^2\|\tilde{\mathbf{X}}_{LS}\|_F^2 = LP_T ∣α∣2∥X~LS∥F2=LPT
∣ α ∣ = L P T ∥ X ~ L S ∥ F 2 = L P T ∥ A † B ∥ F |\alpha| = \sqrt{\frac{LP_T}{\|\tilde{\mathbf{X}}_{LS}\|_F^2}} = \frac{\sqrt{LP_T}}{\|\mathbf{A}^\dagger\mathbf{B}\|_F} ∣α∣=∥X~LS∥F2LPT =∥A†B∥FLPT
取实正值 α \alpha α,最终解为:
X ~ = L P T ∥ A † B ∥ F A † B \tilde{\mathbf{X}} = \frac{\sqrt{LP_T}}{\|\mathbf{A}^\dagger\mathbf{B}\|_F}\mathbf{A}^\dagger\mathbf{B} X~=∥A†B∥FLPT A†B
这一解的几何解释是:首先在无约束意义下找到最优方向 A † B \mathbf{A}^\dagger\mathbf{B} A†B,然后将其长度缩放至满足功率约束的球面上。虽然这不是约束优化问题的严格最优解(最优解需满足KKT条件,涉及拉格朗日乘子的迭代求解),但它提供了一个计算高效的近似解,在实践中性能良好。
A.5 OFDM信号的循环前缀与信道对角化
OFDM系统通过循环前缀(CP)将线性卷积转换为循环卷积,从而实现信道的对角化。设时域多径信道冲激响应为 g = [ g 0 , g 1 , . . . , g L c − 1 ] T g = [g_0, g_1, ..., g_{L_c-1}]^T g=[g0,g1,...,gLc−1]T,其中 L c L_c Lc是信道长度。
不加CP时,接收信号 y = g ∗ x y = g * x y=g∗x(线性卷积),在频域对应:
Y [ k ] = G [ k ] X [ k ] + ICI [ k ] Y[k] = G[k]X[k] + \text{ICI}[k] Y[k]=G[k]X[k]+ICI[k]
其中ICI是载波间干扰项,来自相邻OFDM符号的泄露。
加入长度不小于 L c − 1 L_c - 1 Lc−1的CP后,线性卷积等效于循环卷积 y = g ⊛ x y = g \circledast x y=g⊛x。根据循环卷积定理,在DFT域:
Y [ k ] = G [ k ] X [ k ] , k = 0 , 1 , . . . , M − 1 Y[k] = G[k]X[k], \quad k = 0, 1, ..., M-1 Y[k]=G[k]X[k],k=0,1,...,M−1
其中 G [ k ] = ∑ l = 0 L c − 1 g l e − j 2 π k l / M G[k] = \sum_{l=0}^{L_c-1}g_l e^{-j2\pi kl/M} G[k]=∑l=0Lc−1gle−j2πkl/M是信道的频域响应。这表明每个子载波上的输入输出关系是简单的乘法,等效信道矩阵 D = diag ( G [ 0 ] , G [ 1 ] , . . . , G [ M − 1 ] ) \mathbf{D} = \text{diag}(G[0], G[1], ..., G[M-1]) D=diag(G[0],G[1],...,G[M−1])是对角矩阵。
A.6 MIMO信道矩阵估计的最小二乘分析
在MIMO信道估计中,导频矩阵 P \mathbf{P} P设计为对角矩阵以实现各发射天线的正交训练。考虑存在噪声的情况:
Y p = H P + Z p \mathbf{Y}_p = \mathbf{H}\mathbf{P} + \mathbf{Z}_p Yp=HP+Zp
其中 Y p ∈ C K × N \mathbf{Y}_p \in \mathbb{C}^{K \times N} Yp∈CK×N是接收导频矩阵, Z p ∈ C K × N \mathbf{Z}_p \in \mathbb{C}^{K \times N} Zp∈CK×N是噪声矩阵。
最小二乘估计问题为 min H ∥ Y p − H P ∥ F 2 \min_{\mathbf{H}} \|\mathbf{Y}_p - \mathbf{H}\mathbf{P}\|_F^2 minH∥Yp−HP∥F2,解为:
H ^ = Y p P H ( P P H ) − 1 \hat{\mathbf{H}} = \mathbf{Y}_p\mathbf{P}^H(\mathbf{P}\mathbf{P}^H)^{-1} H^=YpPH(PPH)−1
当 P \mathbf{P} P为对角矩阵 P = diag ( p 1 , . . . , p N ) \mathbf{P} = \text{diag}(p_1, ..., p_N) P=diag(p1,...,pN)时, P P H = diag ( ∣ p 1 ∣ 2 , . . . , ∣ p N ∣ 2 ) \mathbf{P}\mathbf{P}^H = \text{diag}(|p_1|^2, ..., |p_N|^2) PPH=diag(∣p1∣2,...,∣pN∣2)也是对角矩阵。若导频符号等功率( ∣ p n ∣ 2 = P p |p_n|^2 = P_p ∣pn∣2=Pp),则:
H ^ = 1 P p Y p P H \hat{\mathbf{H}} = \frac{1}{P_p}\mathbf{Y}_p\mathbf{P}^H H^=Pp1YpPH
H \^ \] k , n = y k , n p n ∗ ∣ p n ∣ 2 = y k , n p n \[\\hat{\\mathbf{H}}\]_{k,n} = \\frac{y_{k,n}p_n\^\*}{\|p_n\|\^2} = \\frac{y_{k,n}}{p_n} \[H\^\]k,n=∣pn∣2yk,npn∗=pnyk,n 这正是文中式(15)的结果。估计误差 H \~ = H \^ − H = Z p P − 1 \\tilde{\\mathbf{H}} = \\hat{\\mathbf{H}} - \\mathbf{H} = \\mathbf{Z}_p\\mathbf{P}\^{-1} H\~=H\^−H=ZpP−1的方差与噪声功率成正比、与导频功率成反比,因此提高导频功率可改善信道估计精度。 #### A.7 雷达波束图与协方差矩阵的关系 MIMO雷达的发射波束图由信号协方差矩阵决定。定义发射信号协方差矩阵: R = 1 L X \~ X \~ H ∈ C N × N \\mathbf{R} = \\frac{1}{L}\\tilde{\\mathbf{X}}\\tilde{\\mathbf{X}}\^H \\in \\mathbb{C}\^{N \\times N} R=L1X\~X\~H∈CN×N 对于ULA天线阵列,方向 θ \\theta θ上的波束图增益为: P ( θ ) = a H ( θ ) R a ( θ ) P(\\theta) = \\mathbf{a}\^H(\\theta)\\mathbf{R}\\mathbf{a}(\\theta) P(θ)=aH(θ)Ra(θ) 其中 a ( θ ) = \[ 1 , e j π sin θ , e j 2 π sin θ , . . . , e j ( N − 1 ) π sin θ \] T \\mathbf{a}(\\theta) = \[1, e\^{j\\pi\\sin\\theta}, e\^{j2\\pi\\sin\\theta}, ..., e\^{j(N-1)\\pi\\sin\\theta}\]\^T a(θ)=\[1,ejπsinθ,ej2πsinθ,...,ej(N−1)πsinθ\]T是阵列导向矢量(假设半波长间距)。 对于全向波束图设计,目标是 P ( θ ) = P 0 P(\\theta) = P_0 P(θ)=P0(常数)对所有 θ \\theta θ成立。这要求 R ∝ I N \\mathbf{R} \\propto \\mathbf{I}_N R∝IN,即各天线发射正交波形。 对于定向波束图设计,目标是在期望方向 θ 0 \\theta_0 θ0上最大化增益,同时抑制其他方向。这可以通过优化 R \\mathbf{R} R实现,使其主特征向量指向 a ( θ 0 ) \\mathbf{a}(\\theta_0) a(θ0)方向。 在双功能系统中, R \\mathbf{R} R既要满足雷达波束图要求,又要兼顾通信预编码需求,这正是优化问题需要权衡的核心所在。