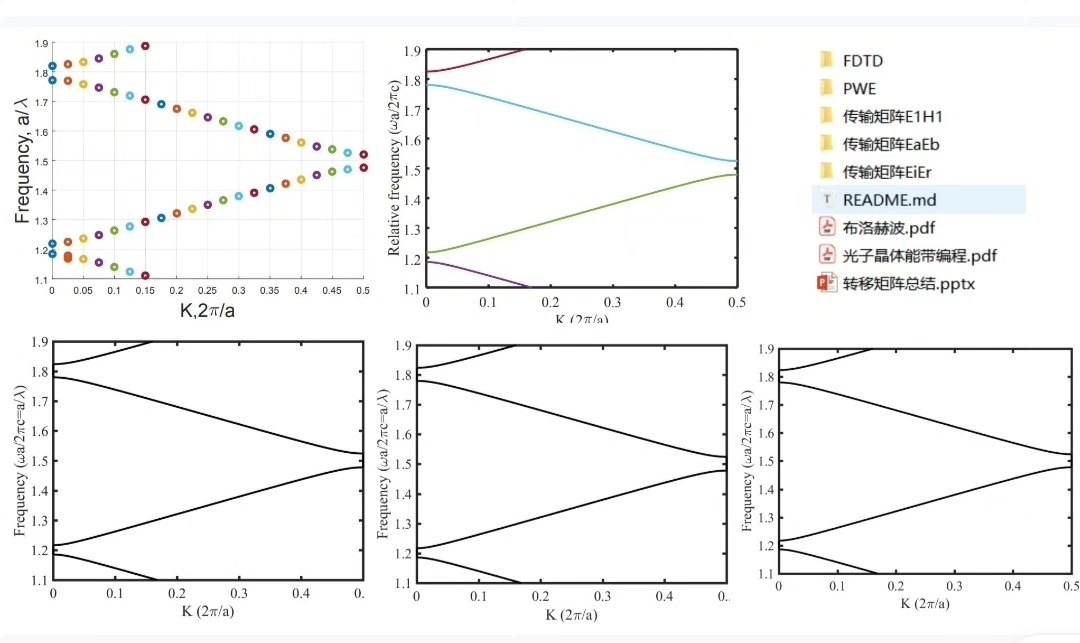
Matlab一维光子晶体能带求解：PWE FDTD及传输矩阵法

Matlab一维光子晶体能带求解，PWE FDTD 传输矩阵等。

一维光子晶体能带计算这事儿听起来高大上，实际用Matlab搞起来其实挺接地气的。今天咱们直接开撸三种常用方法------平面波展开法（PWE）、传输矩阵和FDTD，手把手教你用代码把能带结构抠出来。

平面波展开法：傅里叶暴力美学

PWE的核心就是把介电常数和电磁场用平面波展开，最后整出个本征方程。举个栗子，假设咱们有个周期性排列的介质（比如ε1=4和ε2=9交替），晶格常数a=1。先算介电常数ε的傅里叶系数：

matlab 复制代码

N = 21; % 平面波数量，必须奇数
G = (-(N-1)/2:(N-1)/2)*(2*pi/a);
epsilon = zeros(N,N);
for m = 1:N
    for n = 1:N
        g = G(m) - G(n);
        if g == 0
            epsilon(m,n) = 0.5*(1/4 + 1/9); % 平均介电常数倒数
        else
            epsilon(m,n) = (1/4 - 1/9)*1i/(g*a)*(exp(-1i*g*a/2)-1);
        end
    end
end

这段代码在构造介电常数的傅里叶分量矩阵。注意这里用了介电常数倒数的展开，所以最后出来的矩阵其实是关于1/ε的。接下来构造哈密顿矩阵求本征频率：

matlab 复制代码

k = linspace(0, pi/a, 50); % 第一布里渊区
bands = zeros(length(k), N);
for i = 1:length(k)
    H = (diag(k(i)+G).^2) * inv(epsilon); % 哈密顿矩阵
    bands(i,:) = sqrt(eig(H)); % 频率=sqrt(本征值)
end
plot(k, real(bands), 'b.');

这里有个坑：平面波数量N太小会导致结果不准确，但N太大计算量爆炸。一般先试N=21，如果带隙形状不稳就加量。

传输矩阵：层层套娃的艺术

传输矩阵法特别适合处理多层膜结构。每层用一个2x2矩阵描述电磁波的传递，整个结构就是这些矩阵的连乘。假设咱们有AB两种介质层，厚度d1=0.2a，d2=0.8a：

matlab 复制代码

function T = layer_matrix(epsilon, d, omega)
    k = omega*sqrt(epsilon);
    T = [exp(1i*k*d), 0; 0, exp(-1i*k*d)]; % 传播矩阵
    interface = 0.5*[1+sqrt(epsilon), 1-sqrt(epsilon); 
                    1-sqrt(epsilon), 1+sqrt(epsilon)]; % 界面矩阵
    T = interface \ T * interface; % 组合
end

omega = linspace(0, 5, 300);
trans = zeros(size(omega));
for i = 1:length(omega)
    T_total = eye(2);
    for j = 1:10 % 10个周期
        T_total = T_total * layer_matrix(4, 0.2, omega(i));
        T_total = T_total * layer_matrix(9, 0.8, omega(i));
    end
    trans(i) = 1 / abs(T_total(1,1))^2; % 透射率
end
plot(omega, trans);

这个代码在计算透射谱------带隙对应透射率暴跌的区域。注意当频率ω使矩阵连乘后T(1,1)接近零时，就出现带隙。传输矩阵法的优势是处理缺陷层特别方便，随便插几层进去计算量变化不大。

FDTD：时域硬核模拟

虽然FDTD计算量大，但看着电磁波在晶体里蹦跶实在解压。设置空间网格和时间步长：

matlab 复制代码

Nz = 200; % 空间点数
epsilon = 4*ones(Nz,1);
epsilon(50:50:end) = 9; % 每50格插入高介电层
Ez = zeros(Nz,1); Hy = zeros(Nz,1);
omega_list = []; % 记录激发频率

for t = 1:1e4
    Hy(1:end-1) = Hy(1:end-1) + (Ez(2:end) - Ez(1:end-1))/1; % 空间导数
    Ez(2:end) = Ez(2:end) + (Hy(2:end) - Hy(1:end-1))./epsilon(2:end);
    Ez(Nz/2) = Ez(Nz/2) + sin(0.1*t)*exp(-(t-100)^2/200); % 高斯脉冲激励
    
    if t > 500 % 等稳态后记录
        omega_list = [omega_list; abs(fft(Ez))];
    end
end
spectrum = mean(omega_list,1);
plot(linspace(0,1,length(spectrum)), spectrum);

这里用了软激励源，通过傅里叶变换得到频域响应。带隙对应的频率会在频谱上出现凹陷。FDTD的妙处在于能直接看到电磁场的空间分布，比如带隙频率的场会被强烈局域在缺陷层附近。

三种方法各有骚操作：PWE适合快速扫参数，传输矩阵处理多层结构得心应手，FDTD则是肉眼可见的物理过程。下次老板催你算光子晶体，别犹豫，Matlab三连直接糊他脸上。