进阶数据结构-FenwickTree

前置知识

l o w i t lowit lowit运算
l o w b i t ( x ) lowbit(x) lowbit(x)是取出 x x x作为二进制数的最后一位 1 1 1对应的十进制数字

例如 l o w b i t ( 1 ) = 1 lowbit(1) = 1 lowbit(1)=1, l o w b i t ( 5 ) = 1 lowbit(5) = 1 lowbit(5)=1, l o w b i t ( 8 ) = 8 lowbit(8) = 8 lowbit(8)=8, l o w b i t ( 12 ) = 4 lowbit(12) = 4 lowbit(12)=4

算法能解决的问题

快速求一段数列的前缀和 , 算法时间复杂度 O ( log ⁡ n ) O(\log n) O(logn)
修改某一个位置上的数字 , 算法时间复杂度 O ( log ⁡ n ) O(\log n) O(logn)

算法原理

假设 x x x的二进制表示如下
2 α k + 2 α k − 1 + 2 α k − 2 + . . . + 2 α 1 2 ^ {\alpha _k} + 2 ^ {\alpha _{k - 1}} + 2 ^ {\alpha _{k - 2}} + ... + 2 ^ {\alpha _1} 2αk+2αk−1+2αk−2+...+2α1

不妨设 α k > α k − 1 > α k − 2 > . . . > α 1 , k ≤ log ⁡ x \alpha _k > \alpha _{k - 1} > \alpha _{k - 2} > ... > \alpha _1, k \le \log x αk>αk−1>αk−2>...>α1,k≤logx, 2 α k 2 ^ {\alpha _k} 2αk是 x x x的最高二进制位

可以将 [ 1 , x ] [1, x] [1,x]分为 log ⁡ x \log x logx个小区间

长度为 2 α 1 2 ^ {\alpha _1} 2α1, [ 1 , 2 α 1 ] [1, 2 ^ {\alpha _1}] [1,2α1]
长度为 2 α 2 2 ^ {\alpha _2} 2α2, [ 2 α 1 + 1 ] , 2 α 1 + α 2 ] [2 ^ {\alpha _1} + 1], 2 ^ {\alpha _1 + \alpha _2}] [2α1+1],2α1+α2]
长度为 2 α 3 2 ^ {\alpha _3} 2α3, [ 2 α 1 + α 2 + 1 , 2 α 1 + α 2 + α 3 ] [2 ^ {\alpha _1 + \alpha _2} + 1, 2 ^ {\alpha _1 + \alpha _2 + \alpha _3}] [2α1+α2+1,2α1+α2+α3]
. . . . .... ....

这些区间的共同特点 就是, 如果区间结尾是 t t t, 区间长度 是 l o w b i t ( t ) lowbit(t) lowbit(t)

例如区间 [ 1 , 7 ] = 2 2 + 2 1 + 2 0 [1, 7] = 2 ^ 2 + 2 ^ 1 + 2 ^ 0 [1,7]=22+21+20, 分别进行 l o w b i t ( x ) lowbit(x) lowbit(x)运算后结果就是
l o w b i t ( 7 ) = 1 lowbit(7) = 1 lowbit(7)=1, l o w b i t ( 4 ) = 4 lowbit(4) = 4 lowbit(4)=4, l o w b i t ( 2 ) = 2 lowbit(2) = 2 lowbit(2)=2

分别对应三个区间 [ 7 , 7 ] , [ 5 , 6 ] , [ 1 , 4 ] [7, 7], [5, 6], [1, 4] [7,7],[5,6],[1,4]

我们设当前区间的总和是 c ( x ) c(x) c(x)

有长度是 l o w b i t ( R ) lowbit(R) lowbit(R)并且以 R R R为右端点的区间和是 c ( R ) = S [ R − l o w b i t ( R ) + 1 , R ] c(R) = S[R - lowbit(R) + 1, R] c(R)=S[R−lowbit(R)+1,R]

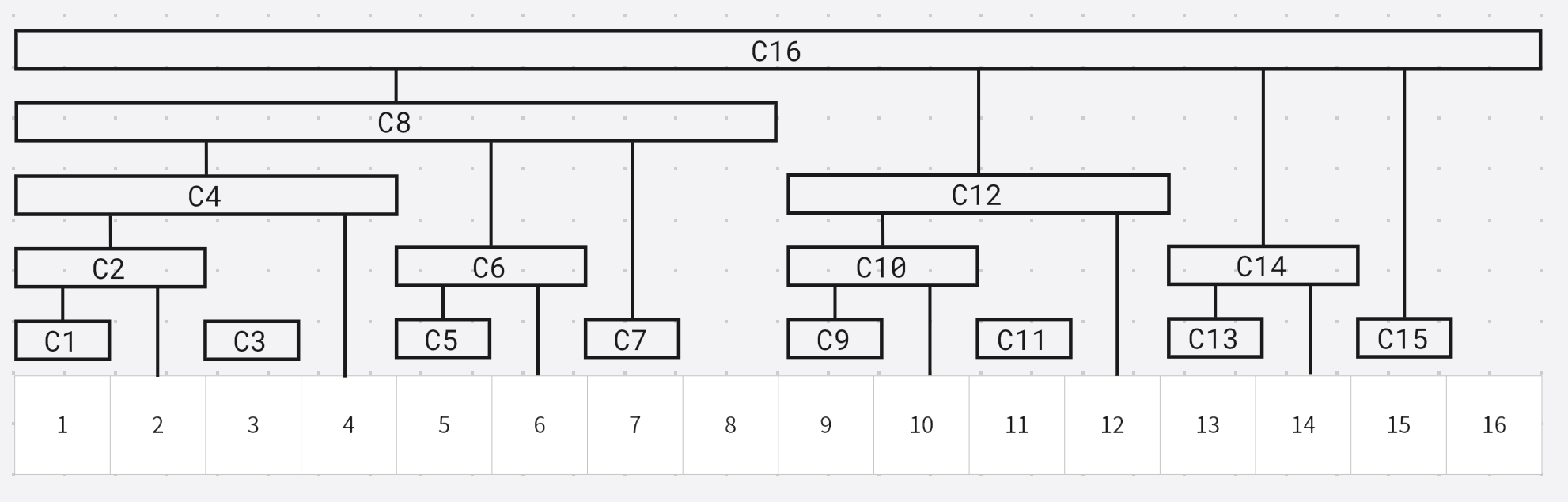
因为上述图中的每一段长度是 l o w b i t ( R ) lowbit(R) lowbit(R)并且以 R R R为右端点

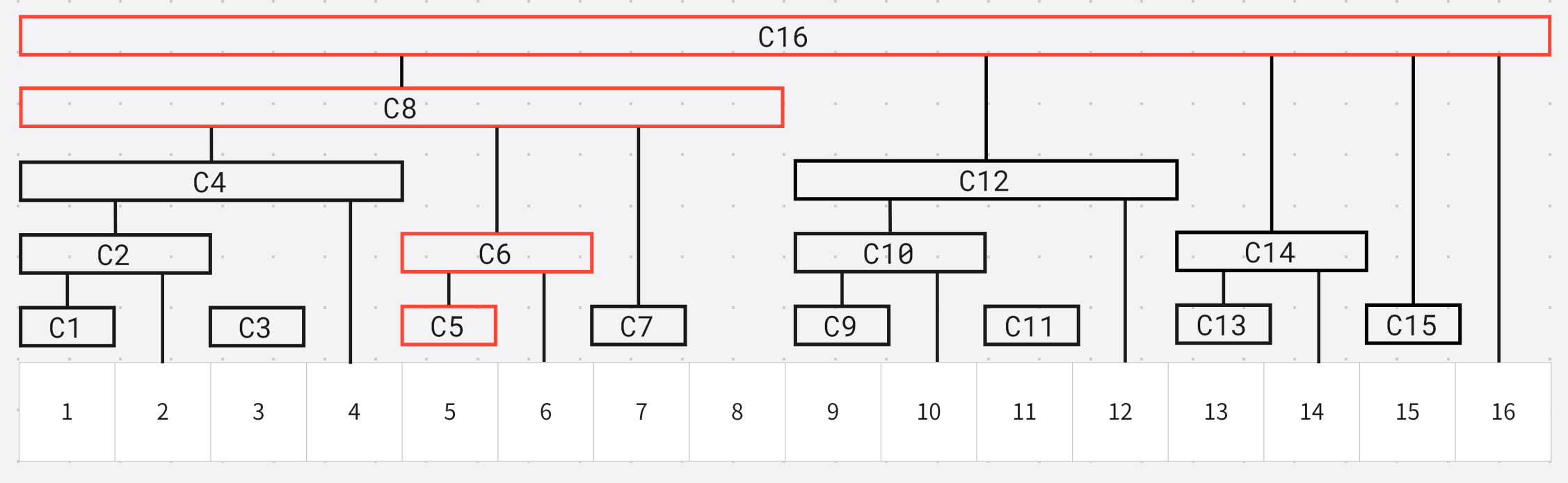
修改 c 5 c_5 c5
5 = 101 5 = 101 5=101, 执行 i = i + l o w b i t ( i ) i = i + lowbit(i) i=i+lowbit(i), 变为 6 6 6, 修改 c 6 c_6 c6
执行 i = i + l o w b i t ( i ) i = i + lowbit(i) i=i+lowbit(i), 变为 8 8 8, 修改 c 8 c_8 c8
执行 i = i + l o w b i t ( i ) i = i + lowbit(i) i=i+lowbit(i), 变为 16 16 16, 修改 c 16 c_{16} c16

可以观察到, 假设修改了某一个位置 a i a_i ai, 那么影响是向上的, i = i + l o w b i t ( i ) i = i + lowbit(i) i=i+lowbit(i)

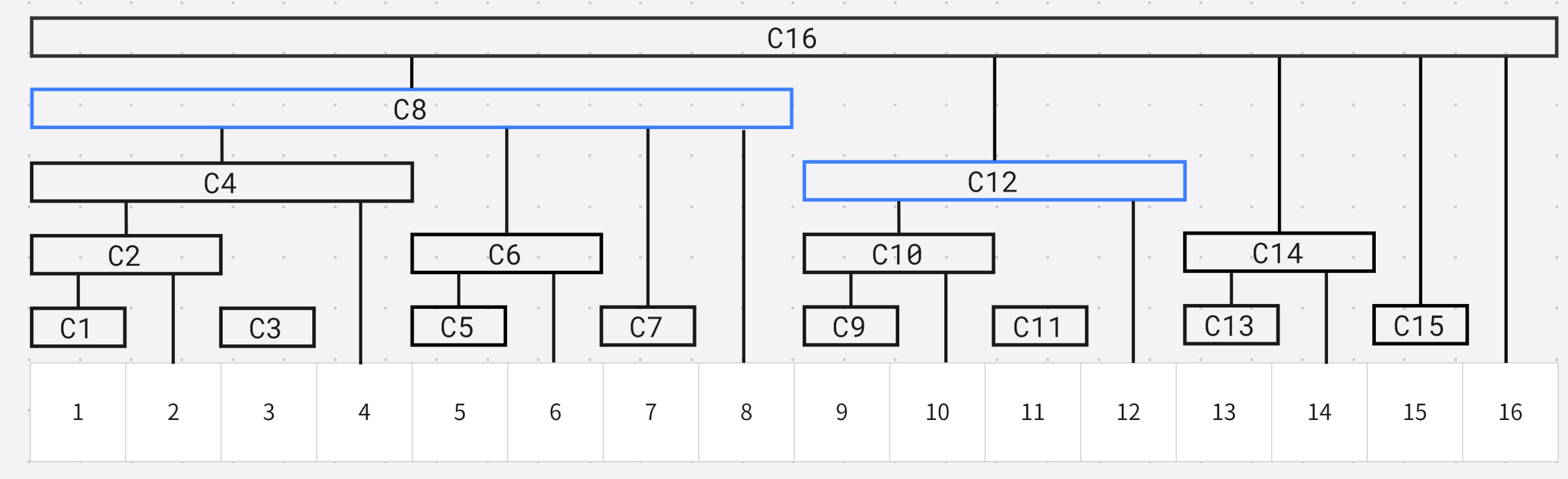
假设计算 12 12 12位置的前缀和 , 12 = 1100 12 = 1100 12=1100, 会首先累加 c 12 c_{12} c12, 然后执行 i = i − l o w b i t ( i ) i = i - lowbit(i) i=i−lowbit(i), 再累加 c 8 c_8 c8

那么结果就是 a n s = c 8 + c 12 ans = c_8 + c_{12} ans=c8+c12, 上图可见结果就是 12 12 12位置的前缀和

可以观察到, 对某个位置求前缀和, i = i − l o w b i t ( i ) i = i - lowbit(i) i=i−lowbit(i)

误区

误区: 求前缀和 c 16 c_{16} c16是 c 8 + c 12 + c 14 + c 15 + a 16 c_8 + c_{12} + c_{14} + c_{15} + a_{16} c8+c12+c14+c15+a16步骤构成的

实际求前缀和的时候并不是执行 c 8 + c 12 + c 14 + c 15 + a 16 c_8 + c_{12} + c_{14} + c_{15} + a_{16} c8+c12+c14+c15+a16, 而是在树状数组初始化或者修改 的时候, c 16 c_{16} c16已经被从下向上 的修改好了, 因此在执行查询操作的时候 , 可以直接返回 t r ( 16 ) tr(16) tr(16), 不需要执行 c 8 + c 12 + c 14 + c 15 + a 16 c_8 + c_{12} + c_{14} + c_{15} + a_{16} c8+c12+c14+c15+a16

算法步骤

实现 l o w b i t ( x ) lowbit(x) lowbit(x)函数
实现初始化/修改操作
实现求前缀和操作

代码实现

F e n w i c k − T r e e Fenwick-Tree Fenwick−Tree模板代码实现

cpp 复制代码

int n;
int tr[N];

int lowbit(int x) {
    return x & -x;
}

void modify(int u, int val) {
    for (int i = u; i <= n; i += lowbit(i)) tr[i] += val;
}

int get(int u) {
    int ans = 0;
    for (int i = u; i; i -= lowbit(i)) {
        ans += tr[i];
    }
    return ans;
}