027动态规划之矩阵DP——算法备赛

矩阵DP

最大正方形

在一个由 '0' 和 '1' 组成的二维矩阵内，找到只包含 '1' 的最大正方形，并返回其面积。

思路分析

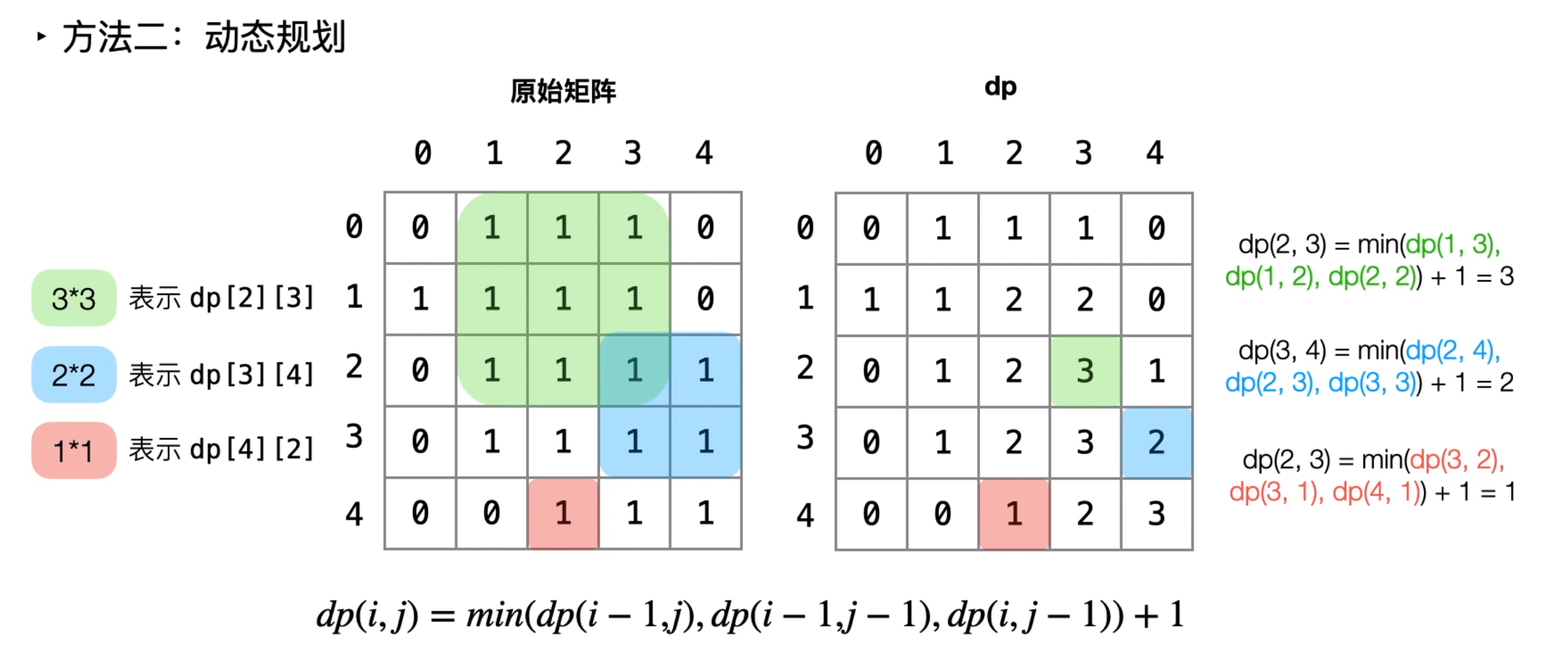
我们用dp(i,j) 表示以 (i,j) 为右下角（选择右下角作为标识，是因为前面遍历时已求出对应dp），且只包含 1 的正方形的边长最大值。如果我们能计算出所有 dp(i,j)的值，那么其中的最大值即为矩阵中只包含 1的正方形的边长最大值，其平方即为最大正方形的面积。

求解dp(i,j)有两种情况：

i或j为0，当(i，j)为1时dp(i,j)为1，(i，j)为0时dp(i，j)为0.
i和j大于0，(i，j)为1，dp(i,j)为 min（dp(i-1,j-1）,dp(i-1,j),dp(i,j-1) )+1

图解

代码

cpp 复制代码

int maximalSquare(vector<vector<char>>& matrix) {
        int s=matrix.size(),s1=matrix[0].size();
        vector<vector<int>>dp(s,vector<int>(s1,0));
        int maxx=0;
        for(int i=0;i<s;i++){
            for(int j=0;j<s1;j++){
                if(matrix[i][j]=='1'){
                    if(i==0||j==0) dp[i][j]=1;
                    else {
                        dp[i][j]=min(dp[i-1][j-1],min(dp[i-1][j],dp[i][j-1]))+1;
                    }
                }
                maxx=max(maxx,dp[i][j]);
            }
        }
        return maxx*maxx;
    }

地下城游戏

问题描述

恶魔们抓住了公主并将她关在了地下城 dungeon 的 右下角 。地下城是由 m x n 个房间组成的二维网格。我们英勇的骑士最初被安置在 左上角 的房间里，他必须穿过地下城并通过对抗恶魔来拯救公主。

骑士的初始健康点数为一个正整数。如果他的健康点数在某一时刻降至 0 或以下，他会立即死亡。

有些房间由恶魔守卫，因此骑士在进入这些房间时会失去健康点数（若房间里的值为负整数 ，则表示骑士将损失健康点数）；其他房间要么是空的（房间里的值为 0 ），要么包含增加骑士健康点数的魔法球（若房间里的值为正整数，则表示骑士将增加健康点数）。

为了尽快解救公主，骑士决定每次只向右或向下移动一步。

返回确保骑士能够拯救到公主所需的最低初始健康点数。

**注意：**任何房间都可能对骑士的健康点数造成威胁，也可能增加骑士的健康点数，包括骑士进入的左上角房间以及公主被监禁的右下角房间。

原题链接

思路分析

定义 dp[i][j] 表示从坐标(i,j)到终点所需的最小初始值 ，也就是说当我们从起点到达坐标(i,j)时，此时我们的路径和要不小于 dp[i][j]。

dp[0][0]就是答案。

在决策dp[i][j]的值时，从往右和往下走的路径中选择所需初始值最小的那一条路径。

dp[i][j]的值为 dp[i+1][j] 和 dp[i][j+1] 中的最小值再减去当前坐标的dungeon(i,j)，但不能小于1，即：

dp[i][j]=max(min(dp[i+1][j],dp[i][j+1])−dungeon(i,j),1)

具体实现时，因为 dp[i][j] 的值与 dp[i+1][j] 和 dp[i][j+1] 有关，应先求 dp[i+1][j] 和 dp[i][j+1] ，所以从右下往左上遍历。

cpp 复制代码

int calculateMinimumHP(vector<vector<int>>& dungeon) {
        int n = dungeon.size(), m = dungeon[0].size();
        vector<vector<int>> dp(n + 1, vector<int>(m + 1, INT_MAX));
        dp[n][m - 1] = dp[n - 1][m] = 1;
        for (int i = n - 1; i >= 0; --i) {
            for (int j = m - 1; j >= 0; --j) {
                int minn = min(dp[i + 1][j], dp[i][j + 1]);
                dp[i][j] = max(minn - dungeon[i][j], 1);
            }
        }
        return dp[0][0];
    }

注意：

「M×N 的网格」「每次只能向右或者向下移动一步」，让人很容易想到该题使用动态规划的方法。

如果惯性地定义dp[i][j]为从起点到(i，j)的最小初始值**，并正向遍历（从左上到右下），会发现，计算「从起点到当前点的最小初始值」还要存储「从出发点到当前点的路径和」，而且确定从起点到(i，j)的最小初始值的路径，它不是影响后面节点dp值的唯一因素 ，换句话说，在计算「从起点到后面节点的最小初始值」时，前面算的dp不会影响决策 。这样的动态规划是不满足「无后效性」的。

因此具体分体要具体分析，不能按惯性思维处理问题。

数字三角形

蓝桥杯2020年省赛题

问题描述

给出一个数字三角形，第一行一个数字，第2行2个数字，...第i行i个数字，如下图：

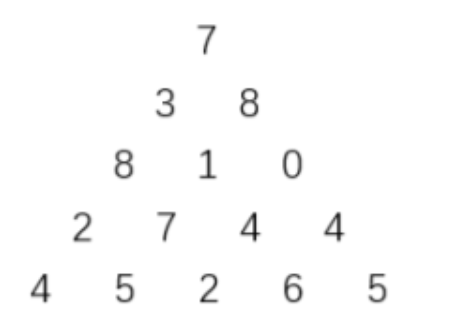
从三角形顶端到三角形底端有很多不同的路径，对于每条路径，把路径上的所有数字加起来得到一个和，请找出最大的路径和。

路径的上的每一步只能从一个数走到下一层和他最近的左边或右边的数。
向左走和向右走的次数相差不能超过1.

**输入：**第一行输入n，代表三角形行数，后面n行，每行输入i（i表示三角形的第几行）个0~100的整数。

**输出：**输出一个整数代表符合要求的最大路径和。

原题链接

思路分析

首先不考虑向左走和向右走的次数相差不能超过1的约束条件

定义二维数组f，f[i][j]表示从顶端走到(i，j)的最大路径和，f[i][j]=max(f[i-1][j-1],f[i-1][j])+d[i][j]

因为向左走和向右走的次数相差不能超过1,且向左走和向右走的次数总和为n-1=cnt

cnt为偶数时，向左走和向右走的次数应都为cnt/2，最后答案就是f[n][n/2+1]
cnt为奇数时，向右走的次数为cnt/2或cnt/2+1，最后答案为max(f[n][n/2],f[n][n/2+1])

代码

cpp 复制代码

#include <iostream>
#include<algorithm>
#include<vector>
#include<queue>
using namespace std;
int main()
{
  // 请在此输入您的代码
  int n; cin>>n;
  vector<vector<int>>d(n+1,vector<int>(n+1));
  vector<vector<int>>f(n+1,vector<int>(n+1));
  for(int i=1;i<=n;i++){
    for(int j=1;j<=i;j++){
      cin>>d[i][j];
    }
  }
  for(int i=1;i<=n;i++){
    for(int j=1;j<=i;j++){
      f[i][j]=max(f[i-1][j-1],f[i-1][j])+d[i][j];  //计算到（i，j）的最大路径和
    }
  }
  int ans=0;
  if((n-1)&1){
    ans=max(f[n][n/2],f[n][n/2+1]);
  }
  else{
    ans=f[n][n/2+1];
  }
  cout<<ans;
}

乘积最大子数组和

问题描述

给你一个整数数组 nums ，请你找出数组中乘积最大的非空连续子数组（该子数组中至少包含一个数字），

并返回该子数组所对应的乘积。

测试用例的答案是一个 32-位 整数。

原题链接

思路分析

考虑当前位置如果是一个负数的话，那么我们希望以它前一个位置结尾的某个段的积 也是个负数，这样就可以负负得正，并且我们希望这个积尽可能「负得更多」，即尽可能小。如果当前位置是一个正数的话，我们更希望以它前一个位置结尾的某个段的积也是个正数，并且希望它尽可能地大。

动态维护两个数组maxf，minf. maxf[i]表示以i结尾的连续子数组的最大乘积 minf[i]表示以i结尾的连续子数组的最小乘积

考虑到第i的状态只与第i-1的状态有关，可参考滚动数组进行空间复杂度优化，

minf表示以前一个元素结尾的连续子数组的最小乘积

maxf表示以前一个元素结尾的连续子数组的最大乘积

代码

cpp 复制代码

int maxProduct(vector<int>& nums) {
        int maxF = nums[0], minF = nums[0], ans = nums[0];
        for (int i = 1; i < nums.size(); ++i) {
            int mx = maxF, mn = minF;  //先把上一个元素结尾的连续子数组的最大，最小乘积取出来。
            //更新 maxf，minf。
            maxF = max(mx * nums[i], max(nums[i], mn * nums[i]));//三个数中取最大值，都包含有nums[i],符合循环不变式
            minF = min(mn * nums[i], min(nums[i], mx * nums[i]));
            ans = max(maxF, ans);
        }
        return ans;
    }

扣分后的最大得分

问题描述

给你一个 m x n 的整数矩阵 points （下标从 0 开始）。一开始你的得分为 0 ，你想最大化从矩阵中得到的分数。

你的得分方式为：每一行 中选取一个格子，选中坐标为 (r, c) 的格子会给你的总得分增加 points[r][c] 。

然而，相邻行之间 被选中的格子如果隔得太远，你会失去一些得分。对于相邻行 r 和 r + 1 （其中 0 <= r < m - 1），选中坐标为 (r, c1) 和 (r + 1, c2) 的格子，你的总得分减少 abs(c1 - c2) 。

请你返回你能得到的最大得分。

原题链接

思路分析

定义 f[i][j] 表示前 i 行中，第 i 行选择points[i][j]时的最大得分。

状态转移方程为：f[i][j]=points[i][j]+max{ f[i−1][k]−∣k−j∣}

最后的max{f[n-1][j]}就是答案。

由于转移的时间复杂度是 O(n) 的，所以总体时间复杂度是 O(mn^2) 的，我们需要优化。

去掉绝对值符号，将上式变形为：

f[i][j]=points[i][j]+

max{f[i−1][k]−(j−k)},k<=j
max{f[i−1][k]−(k-j)},k>j

由上式可知，在计算 f[i][j]时，我们需要知道位置 j 左侧的 f[i−1][k]+k 的最大值，以及位置 j 右侧的 f[i−1][k]−k 的最大值。这可以在计算完一整行 f[i−1] 之后，在计算下一行 f[i] 之前，可以预处理出来。具体实现上更巧妙一些。

这样优化后，转移就从 O(n) 降为 O(1)，于是总时间复杂度为 O(mn)。

由于求解f[i]只与f[i-1]有关，所以可用交替滚动优化空间复杂度为O(n).

代码

cpp 复制代码

long long maxPoints(vector<vector<int>>& points) {
        long long ans=0;
        int n=points.size(),m=points[0].size();
        vector<vector<long long>>dp(2,vector<long long>(m));
        int now=0,old=1;

        for(int i=0;i<n;i++){
            long long maxn=0;
            for(int j=0;j<m;j++){
                maxn=max(maxn-1,dp[old][j]);
                dp[now][j]=maxn;  //j左侧的 f[i−1][k]-j+k 最大值
            }
            for(int j=m-1;j>=0;j--){
                maxn=max(maxn-1,dp[old][j]);
                //max(maxn,dp[now][j]) 为 max{ f[i−1][k]−∣k−j∣}
                dp[now][j]=max(maxn,dp[now][j])+points[i][j];
            }
            swap(now,old);
        }

        for(auto i:dp[old]){
            ans=max(i,ans);
        }
        return ans;
}