论文阅读——Edge Impulse：面向微型机器学习的MLOps平台

Edge Impulse：面向微型机器学习的MLOps平台深度解析

Hymel S, Banbury C, Situnayake D, et al. Edge impulse: An mlops platform for tiny machine learning[J]. arXiv preprint arXiv:2212.03332, 2022.

一、引言与研究背景

Edge Impulse作为一个革命性的云端机器学习运维（MLOps）平台，正在重新定义嵌入式和边缘机器学习（TinyML）系统的开发范式。该平台解决了长期困扰TinyML领域的核心问题：软件栈的严重碎片化和部署硬件的极度异构性。这些问题使得机器学习模型的优化变得异常困难，且优化结果往往不可移植。截至2022年10月的统计数据显示，Edge Impulse已经托管了来自50,953名开发者的118,185个项目，这一数字充分证明了该平台在产业界的广泛接受度和实用价值。

机器学习技术在嵌入式系统中的应用正在经历爆炸式增长。从低功耗设备上的唤醒词检测（如"OK Google"、"Alexa"等），到工业环境中的预测性维护，从传感器网络中的异常检测到边缘设备上的视觉目标检测，再到可穿戴设备中的人体活动识别，TinyML正在重塑物联网生态系统。根据全球技术情报公司ABI Research的预测，配备边缘AI芯片组的设备安装基数将在2025年超过50亿台，而整个嵌入式机器学习市场预计到2027年将达到443亿美元的规模。这种增长趋势背后，是对高效、可扩展的TinyML开发平台的迫切需求。

二、嵌入式机器学习生态系统的核心挑战

2.1 设备资源约束的深层分析

TinyML系统由于其小尺寸、低成本和严格的能源预算，通常具有极其有限的计算能力。微控制器作为TinyML领域最常见的通用处理器，其时钟速度通常远低于移动或服务器级别的处理器，且架构特性也更为简单。例如，一个典型的Cortex-M4微控制器可能只有64MHz的时钟频率，256KB的SRAM和1MB的闪存，这与动辄几GHz频率、几GB内存的服务器形成鲜明对比。

机器学习工作负载通常需要数GB的工作内存和存储空间来存储激活值和模型权重，但TinyML系统通常只配备几百KB的SRAM和几MB的eFlash。这种严格的约束对模型设计提出了极高要求。更复杂的是，TinyML系统通常具有非常平坦的内存层次结构，由于缓存很小或不存在，且通常没有片外内存，传统神经网络设计所依赖的数据访问模式不再适用，这迫使研究者设计全新的模型架构。

另一方面，能源效率也是另一个关键约束。许多TinyML应用依靠电池供电，而系统的电池寿命直接影响应用的实用性。由于TinyML系统的小尺寸和低成本，这些电池通常很小且容量有限（例如纽扣电池）。任何无线传输都可能快速耗尽电池，因此只有在做出特定预测时才传输数据变得至关重要。这意味着模型的准确性直接影响系统的能源消耗------误报会导致不必要的能源消耗。

2.2 硬件异构性的复杂性

尽管资源限制在TinyML硬件中相当普遍，但嵌入式计算系统本身却极其多样化。TinyML设备范围从微控制器和数字信号处理器，到特定应用加速器和神经形态处理器。仅以STM32 32位Arm Cortex MCU系列为例，就包括17个不同的系列，每个系列基于不同的ARM处理器核心（Cortex-M7、Cortex-M4、Cortex-M33、Cortex-M3、Cortex-M0+或Cortex-M0），它们在指令集架构层面的能力也各不相同。

每个硬件平台支持不同的部署过程、模型类型、数值格式和内存访问模式，这使得TinyML应用难以跨设备移植。当创建需要部署到各种设备的大规模应用时，这种复杂性会进一步加剧，每种设备都有自己的库和部署方法。这种异构性不仅增加了开发成本，还严重限制了优化技术的可重用性。

2.3 软件栈的碎片化问题

由于TinyML领域的相对年轻，软件栈在特定格式和最佳实践方面尚未达到稳定状态。TinyML应用有时使用完整的操作系统（如Linux），有时使用实时操作系统（如Zephyr），有时使用推理框架（如TFLM），甚至有时作为没有外部依赖的C++库的裸机实现。这种多样性限制了新优化和工具的互操作性。

标准的TinyML训练流程整合了来自多个源的工具和技术，导致软件版本和端口的复杂网络，这可能阻碍协作、可移植性、稳健性和可重复性。即使不考虑模型超参数和量化等优化，跨项目应用一致的预处理也是一个复杂的超参数混合体，通常需要对信号有深入的、特定领域的见解。

三、Edge Impulse平台架构与核心设计

3.1 整体架构概览

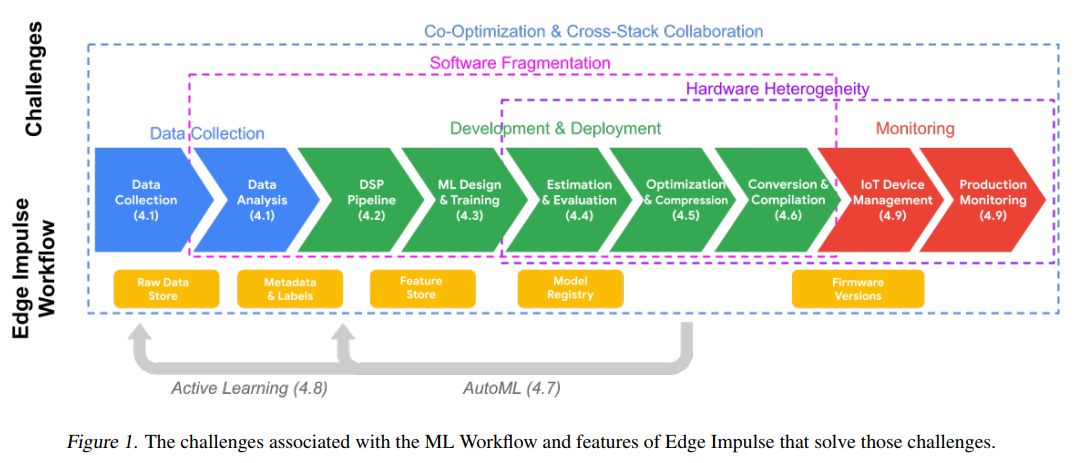
图1描述：机器学习工作流挑战与Edge Impulse解决方案

图1展示了Edge Impulse如何系统性地解决TinyML开发中的各个挑战。图的上半部分标识了五大类挑战，用不同颜色标注：协同优化与跨栈协作（紫色）、软件碎片化（粉色）、硬件异构性（绿色）、监控挑战（橙色）和生产/监控（红色）。下半部分展示了Edge Impulse的工作流程，从数据收集开始，经过数据分析、DSP流水线、ML设计与训练、估计与评估、优化与压缩、转换与编译，最终到IoT设备管理和生产监控。每个阶段都有相应的支持模块，如原始数据开始、变量和标签、特征探索器、模型注册表、性能分析器等。图中还显示了主动学习和AutoML的反馈循环，这些循环贯穿整个工作流程。

3.2 Studio项目界面与数据流

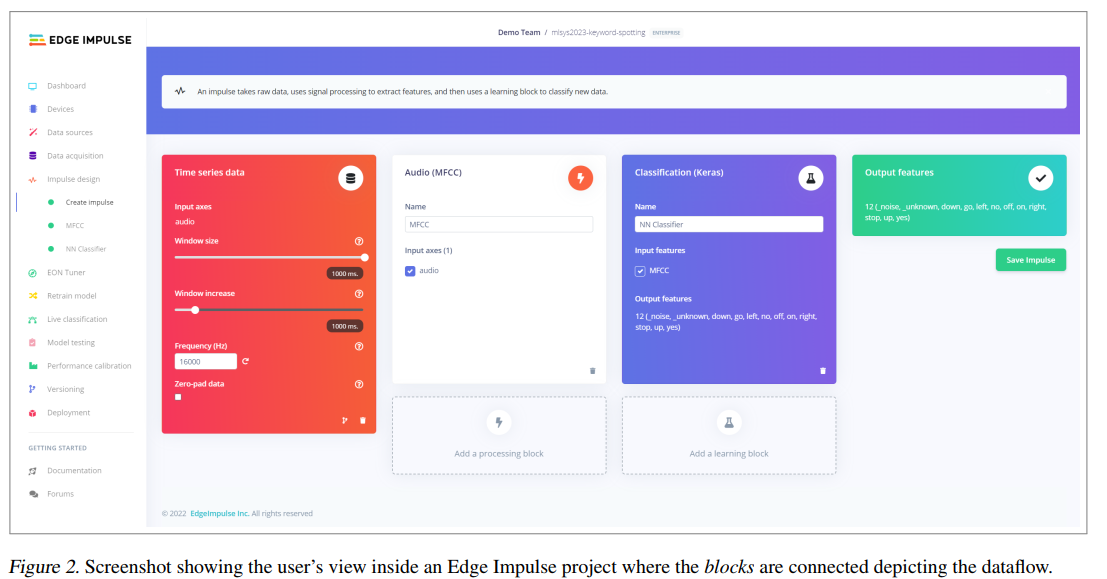
图2描述：Edge Impulse Studio项目内部视图

图2展示了用户在Edge Impulse Studio中的实际工作界面。界面主要分为三个功能区域：左侧是项目导航菜单（包括Dashboard、Devices、Data acquisition、DSP Tuner等选项），中间是主要工作区域，显示了三个相互连接的处理块。第一个红色块是"Time series data"（时间序列数据），显示输入音频的参数设置；第二个蓝色块是"Audio (MFCC)"（音频MFCC处理），展示分类特征的配置；第三个绿色块是"Classification (Keras)"（Keras分类器），显示输出特征的设置。每个块都有详细的参数配置选项，用户可以通过拖拽和连接这些块来构建自己的机器学习流水线。顶部的搜索栏允许用户快速查找和添加新的处理块。

3.3 设计目标与原则

Edge Impulse的设计遵循七个核心原则，每个原则都针对特定的开发挑战：

可访问性原则：平台的首要目标是降低嵌入式机器学习的技术门槛，同时专注于为资源受限设备生产高质量的TinyML解决方案。通过提供直观的图形界面和智能的默认配置，平台使嵌入式工程师能够快速掌握机器学习概念，同时帮助机器学习工程师理解嵌入式系统的约束。

端到端集成：平台提供了完整的机器学习工作流支持，从数据收集到模型部署的每个环节都有相应的工具和接口。用户或团队可以在统一的环境中收集数据集、训练优化模型、评估性能并部署嵌入式固件。

数据中心化方法：鉴于传感器数据集在嵌入式生态系统中的稀缺性，Edge Impulse优先考虑数据中心化方法。平台支持从各种源摄取数据，包括实时传感器流、批量上传和云存储集成。这种方法鼓励开发者更多地关注数据质量和特征工程，而不是过度依赖模型架构的复杂性。

迭代开发支持：跨栈优化的关键在于快速的开发者反馈循环。Edge Impulse提供了丰富的AutoML工具集，使开发者能够快速实验不同的设计空间优化。短设计周期和自动化工具减少了专业知识的负担，使非专家也能开发高质量的TinyML应用。

四、数字信号处理流水线的理论基础

4.1 信号处理的数学原理

Edge Impulse的DSP流水线实现了多种高效的信号处理算法。对于音频信号处理，平台支持梅尔频率倒谱系数（MFCC）和梅尔滤波器组能量（MFE）等特征提取方法。

MFCC的计算过程涉及多个数学变换。首先，对输入信号x(n)x(n)x(n)进行短时傅里叶变换（STFT）：

X(k,m)=∑n=0N−1x(n+mH)⋅w(n)⋅e−j2πkn/NX(k, m) = \sum_{n=0}^{N-1} x(n + mH) \cdot w(n) \cdot e^{-j2\pi kn/N}X(k,m)=n=0∑N−1x(n+mH)⋅w(n)⋅e−j2πkn/N

其中w(n)w(n)w(n)是窗函数（通常使用汉明窗），HHH是帧移，mmm是帧索引。汉明窗的定义为：

w(n)=0.54−0.46cos⁡(2πnN−1)w(n) = 0.54 - 0.46\cos\left(\frac{2\pi n}{N-1}\right)w(n)=0.54−0.46cos(N−12πn)

接下来，计算功率谱密度：

P(k,m)=∣X(k,m)∣2NP(k, m) = \frac{|X(k, m)|^2}{N}P(k,m)=N∣X(k,m)∣2

然后应用梅尔滤波器组。梅尔尺度与频率的关系为：

mel(f)=2595⋅log⁡10(1+f700)\text{mel}(f) = 2595 \cdot \log_{10}\left(1 + \frac{f}{700}\right)mel(f)=2595⋅log10(1+700f)

滤波器组的输出经过对数变换后，应用离散余弦变换（DCT）得到MFCC系数：

c(i)=∑j=1Mlog⁡(E(j))⋅cos⁡[i(j−0.5)πM]c(i) = \sum_{j=1}^{M} \log(E(j)) \cdot \cos\left[\frac{i(j-0.5)\pi}{M}\right]c(i)=j=1∑Mlog(E(j))⋅cos[Mi(j−0.5)π]

其中E(j)E(j)E(j)是第jjj个梅尔滤波器的能量输出，MMM是滤波器数量。

4.2 预处理优化策略

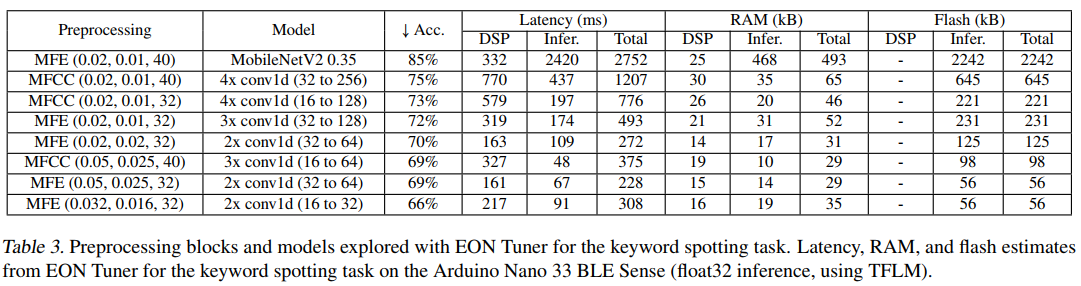
Edge Impulse通过精心设计的预处理策略显著提高了系统效率。表3详细展示了不同预处理配置对系统性能的影响。例如，使用MFE(0.02, 0.01, 40)配合MobileNetV2可以达到85%的准确率，但需要2752ms的总延迟和493KB的RAM。相比之下，MFE(0.05, 0.025, 32)配合2x conv1d(32 to 64)虽然准确率降至69%，但总延迟仅为228ms，RAM使用仅为29KB。

这种权衡关系可以用帕累托优化理论来描述。定义性能向量P=(accuracy,−latency,−memory)\mathbf{P} = (\text{accuracy}, -\text{latency}, -\text{memory})P=(accuracy,−latency,−memory)，帕累托前沿上的点满足：

∄P′:Pi′≥Pi ∀i∧∃j:Pj′>Pj\nexists \mathbf{P}' : P'_i \geq P_i \, \forall i \land \exists j : P'_j > P_j∄P′:Pi′≥Pi∀i∧∃j:Pj′>Pj

五、AutoML与超参数优化的数学框架

5.1 EON Tuner的优化算法

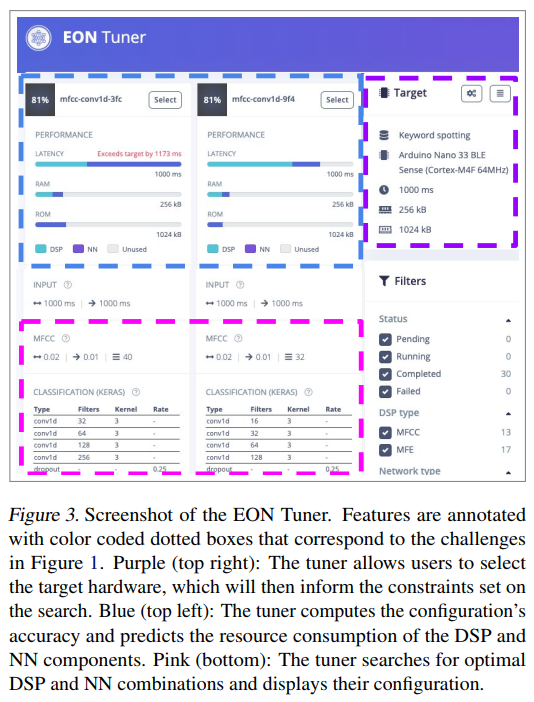
图3描述：EON Tuner界面与功能

图3展示了EON Tuner运行后的结果界面。顶部的紫色区域显示了目标硬件选择（如Arduino Nano 33 BLE Sense），这将决定搜索的约束条件。左侧的蓝色区域展示了各种配置的准确率以及DSP和神经网络组件的资源消耗预测。主界面显示了多个配置选项，每个选项都有详细的性能指标条形图，包括延迟（Latency）、RAM使用和Flash使用。底部的粉色区域详细列出了每个配置的DSP和NN组合参数，如MFCC设置、卷积层数量等。右侧的过滤器允许用户根据性能要求筛选配置。

EON Tuner使用贝叶斯优化来高效探索超参数空间。给定超参数θ\thetaθ和观察到的性能yyy，构建高斯过程模型：

f(θ)∼GP(μ(θ),k(θ,θ′))f(\theta) \sim \mathcal{GP}(\mu(\theta), k(\theta, \theta'))f(θ)∼GP(μ(θ),k(θ,θ′))

其中均值函数μ(θ)\mu(\theta)μ(θ)和协方差函数k(θ,θ′)k(\theta, \theta')k(θ,θ′)定义了先验分布。采集函数（如Expected Improvement）指导下一个评估点的选择：

EI(θ)=E[max⁡(f(θ)−f(θ∗),0)]\text{EI}(\theta) = \mathbb{E}[\max(f(\theta) - f(\theta^*), 0)]EI(θ)=E[max(f(θ)−f(θ∗),0)]

其中f(θ∗)f(\theta^*)f(θ∗)是当前最佳观察值。

5.2 多目标优化框架

Edge Impulse的优化问题本质上是多目标的，需要在准确率、延迟、内存使用等多个指标间平衡。定义多目标优化问题：

minimizeF(θ)=[f1(θ),f2(θ),...,fk(θ)]Tsubject togi(θ)≤0,i=1,...,mhj(θ)=0,j=1,...,p\begin{aligned} \text{minimize} \quad & \mathbf{F}(\theta) = [f_1(\theta), f_2(\theta), \ldots, f_k(\theta)]^T \\ \text{subject to} \quad & g_i(\theta) \leq 0, \quad i = 1, \ldots, m \\ & h_j(\theta) = 0, \quad j = 1, \ldots, p \end{aligned}minimizesubject toF(θ)=[f1(θ),f2(θ),...,fk(θ)]Tgi(θ)≤0,i=1,...,mhj(θ)=0,j=1,...,p

其中f1f_1f1可能是负准确率，f2f_2f2是延迟，f3f_3f3是内存使用。约束条件ggg和hhh代表硬件限制。

使用加权切比雪夫方法将多目标问题转化为单目标：

minimizemax⁡i=1,...,k{λi∣fi(θ)−zi∗∣}\text{minimize} \max_{i=1,\ldots,k} \{\lambda_i |f_i(\theta) - z_i^*|\}minimizei=1,...,kmax{λi∣fi(θ)−zi∗∣}

其中z∗z^*z∗是理想点，λ\lambdaλ是权重向量。

六、模型压缩与量化的理论分析

6.1 量化的数学基础

Edge Impulse实现了多种量化策略来减少模型大小和推理时间。对于均匀量化，实数值rrr到量化值qqq的映射定义为：

q=clamp(round(rs)+z,qmin⁡,qmax⁡)q = \text{clamp}\left(\text{round}\left(\frac{r}{s}\right) + z, q_{\min}, q_{\max}\right)q=clamp(round(sr)+z,qmin,qmax)

其中sss是缩放因子，zzz是零点，clamp函数确保输出在有效范围内。

缩放因子和零点的计算基于权重或激活的分布：

s=rmax⁡−rmin⁡qmax⁡−qmin⁡s = \frac{r_{\max} - r_{\min}}{q_{\max} - q_{\min}}s=qmax−qminrmax−rmin

z=round(qmin⁡−rmin⁡s)z = \text{round}\left(q_{\min} - \frac{r_{\min}}{s}\right)z=round(qmin−srmin)

量化误差的期望值可以通过积分计算：

E[ε]=∫(r−r′)2p(r)dr\mathbb{E}[\varepsilon] = \int (r - r')^2 p(r) drE[ε]=∫(r−r′)2p(r)dr

其中p(r)p(r)p(r)是权重或激活的概率分布。

6.2 EON编译器的优化策略

EON编译器通过消除解释器开销来优化推理。传统TFLM的推理过程包含解释器开销OinterpO_{\text{interp}}Ointerp，而EON直接生成本地代码，总延迟从：

TTFLM=Tpreprocess+Tinference+OinterpT_{\text{TFLM}} = T_{\text{preprocess}} + T_{\text{inference}} + O_{\text{interp}}TTFLM=Tpreprocess+Tinference+Ointerp

减少到：

TEON=Tpreprocess+Tinference_optimizedT_{\text{EON}} = T_{\text{preprocess}} + T_{\text{inference\_optimized}}TEON=Tpreprocess+Tinference_optimized

其中Tinference_optimized<TinferenceT_{\text{inference\optimized}} < T{\text{inference}}Tinference_optimized<Tinference由于编译时优化。

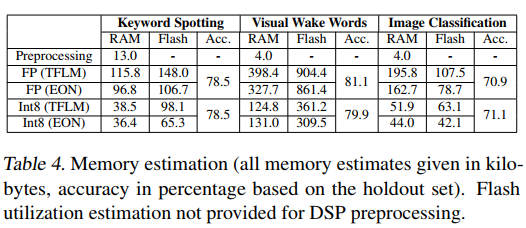
表4的数据验证了这种优化的效果。例如，关键词检测任务使用浮点TFLM需要115.8KB RAM，而int8 EON仅需36.4KB，减少了68.6%。

七、跨硬件性能分析

7.1 延迟分解分析

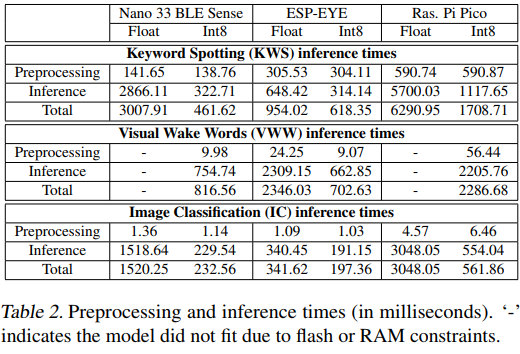
表2展示了三种硬件平台的详细延迟分解。以关键词检测为例，在Nano 33 BLE Sense上：

预处理延迟：Tpre=141.65msT_{\text{pre}} = 141.65\text{ms}Tpre=141.65ms（浮点）
推理延迟：Tinf=2866.11msT_{\text{inf}} = 2866.11\text{ms}Tinf=2866.11ms（浮点）
总延迟：Ttotal=3007.91msT_{\text{total}} = 3007.91\text{ms}Ttotal=3007.91ms

量化后的改进率：

Speedup=TfloatTint8=3007.91461.62=6.52×\text{Speedup} = \frac{T_{\text{float}}}{T_{\text{int8}}} = \frac{3007.91}{461.62} = 6.52\timesSpeedup=Tint8Tfloat=461.623007.91=6.52×

这种加速主要来自于：

减少的内存带宽需求（4字节浮点 vs 1字节整数）
SIMD指令的更好利用
更高的缓存命中率

7.2 内存层次结构的影响

不同硬件的内存层次结构显著影响性能。定义内存访问成本模型：

Cmem=nL1⋅tL1+nL2⋅tL2+nRAM⋅tRAMC_{\text{mem}} = n_{L1} \cdot t_{L1} + n_{L2} \cdot t_{L2} + n_{\text{RAM}} \cdot t_{\text{RAM}}Cmem=nL1⋅tL1+nL2⋅tL2+nRAM⋅tRAM

其中nLin_{Li}nLi是对第iii级缓存的访问次数，tLit_{Li}tLi是相应的访问延迟。

对于扁平内存结构的微控制器：

Cmem_MCU≈ntotal⋅tRAMC_{\text{mem\MCU}} \approx n{\text{total}} \cdot t_{\text{RAM}}Cmem_MCU≈ntotal⋅tRAM

这解释了为什么某些优化在微控制器上的效果不如在具有复杂缓存层次的处理器上明显。

八、实际应用案例的深入分析

8.1 Oura Ring睡眠跟踪系统

Oura Ring的睡眠阶段分类使用了基于生理信号的深度学习模型。该系统处理多模态传感器数据，包括：

心率变异性（HRV）：采样率250Hz
体温：采样率1Hz
加速度计：采样率50Hz

特征提取过程使用滑动窗口方法，窗口大小w=30w=30w=30秒，重叠率50%。对于HRV信号，计算时域和频域特征：

时域特征：

RMSSD=1N−1∑i=1N−1(RRi+1−RRi)2\text{RMSSD} = \sqrt{\frac{1}{N-1} \sum_{i=1}^{N-1} (RR_{i+1} - RR_i)^2}RMSSD=N−11i=1∑N−1(RRi+1−RRi)2

pNN50=count(∣RRi+1−RRi∣>50ms)N×100%\text{pNN50} = \frac{\text{count}(|RR_{i+1} - RR_i| > 50\text{ms})}{N} \times 100\%pNN50=Ncount(∣RRi+1−RRi∣>50ms)×100%

频域特征通过Lomb-Scargle周期图计算，适合处理不均匀采样的RR间期数据：

P(ω)=12σ2[(∑xicos⁡(ω(ti−τ)))2∑cos⁡2(ω(ti−τ))+(∑xisin⁡(ω(ti−τ)))2∑sin⁡2(ω(ti−τ))]P(\omega) = \frac{1}{2\sigma^2}\left[\frac{\left(\sum x_i\cos(\omega(t_i-\tau))\right)^2}{\sum\cos^2(\omega(t_i-\tau))} + \frac{\left(\sum x_i\sin(\omega(t_i-\tau))\right)^2}{\sum\sin^2(\omega(t_i-\tau))}\right]P(ω)=2σ21[∑cos2(ω(ti−τ))(∑xicos(ω(ti−τ)))2+∑sin2(ω(ti−τ))(∑xisin(ω(ti−τ)))2]

最终模型达到79%的分类准确率，与多导睡眠图的一致性相当。

九、平台生态系统与社区影响

9.1 教育影响的量化分析

Edge Impulse在教育领域的影响可以通过学习曲线模型量化。定义学习效率函数：

L(t)=L∞(1−e−t/τ)L(t) = L_{\infty}(1 - e^{-t/\tau})L(t)=L∞(1−e−t/τ)

其中L∞L_{\infty}L∞是渐近学习水平，τ\tauτ是学习时间常数。

传统方法的τtraditional≈120\tau_{\text{traditional}} \approx 120τtraditional≈120小时，而使用Edge Impulse的τEI≈40\tau_{\text{EI}} \approx 40τEI≈40小时，学习效率提升：

η=τtraditionalτEI=3×\eta = \frac{\tau_{\text{traditional}}}{\tau_{\text{EI}}} = 3\timesη=τEIτtraditional=3×

这解释了为什么超过75,000名学生能够在相对短的时间内掌握TinyML技术。

9.2 开源贡献的网络效应

Edge Impulse的开源策略产生了显著的网络效应。根据梅特卡夫定律，网络价值与用户数的平方成正比：

V=k⋅n2V = k \cdot n^2V=k⋅n2

其中kkk是价值系数，nnn是活跃用户数。

考虑到3,219个公开项目和50,953名开发者，平台的潜在价值：

Vpotential=k⋅(50,953)2≈2.6×109kV_{\text{potential}} = k \cdot (50,953)^2 \approx 2.6 \times 10^9 kVpotential=k⋅(50,953)2≈2.6×109k

这种网络效应加速了最佳实践的传播和技术创新。

十、与其他平台的比较分析

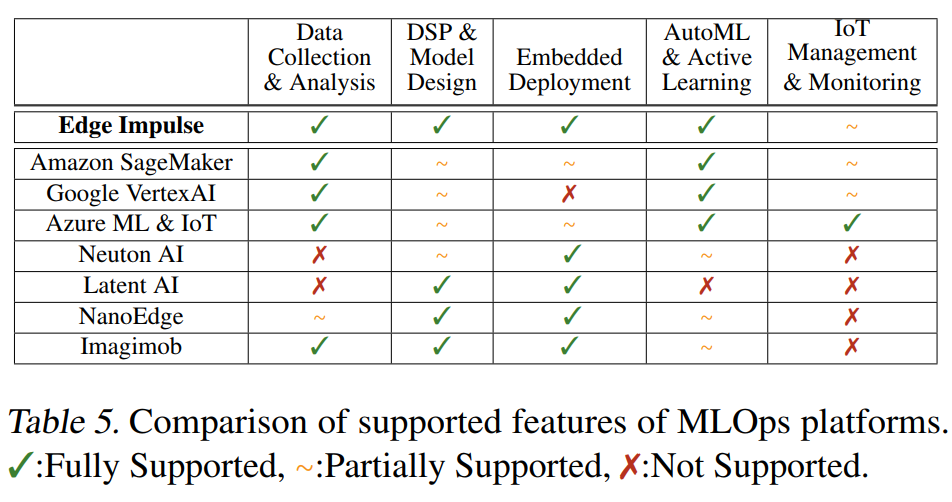
表5提供了Edge Impulse与其他MLOps平台的功能对比。定义功能完整性指标：

Completeness=∑iwi⋅fi\text{Completeness} = \sum_i w_i \cdot f_iCompleteness=i∑wi⋅fi

其中wiw_iwi是第iii个功能的权重，fi∈{0,0.5,1}f_i \in \{0, 0.5, 1\}fi∈{0,0.5,1}表示不支持、部分支持或完全支持。

对于TinyML应用，假设权重分布为：

数据收集与分析：w1=0.25w_1 = 0.25w1=0.25
DSP与模型设计：w2=0.30w_2 = 0.30w2=0.30
嵌入式部署：w3=0.25w_3 = 0.25w3=0.25
AutoML：w4=0.15w_4 = 0.15w4=0.15
IoT管理：w5=0.05w_5 = 0.05w5=0.05

Edge Impulse的完整性得分：

CEI=0.25×1+0.30×1+0.25×1+0.15×1+0.05×0.5=0.975C_{\text{EI}} = 0.25 \times 1 + 0.30 \times 1 + 0.25 \times 1 + 0.15 \times 1 + 0.05 \times 0.5 = 0.975CEI=0.25×1+0.30×1+0.25×1+0.15×1+0.05×0.5=0.975

相比之下，Amazon SageMaker的得分：

CAWS=0.25×1+0.30×0.5+0.25×0.5+0.15×1+0.05×0.5=0.70C_{\text{AWS}} = 0.25 \times 1 + 0.30 \times 0.5 + 0.25 \times 0.5 + 0.15 \times 1 + 0.05 \times 0.5 = 0.70CAWS=0.25×1+0.30×0.5+0.25×0.5+0.15×1+0.05×0.5=0.70

这种量化分析清楚地展示了Edge Impulse在TinyML领域的综合优势。

十一、未来发展方向与技术展望

11.1 神经架构搜索的集成

未来的Edge Impulse版本可能集成更先进的神经架构搜索（NAS）算法。基于可微分架构搜索（DARTS）的方法特别适合资源受限环境：

min⁡αLval(w∗(α),α)s.t.w∗(α)=arg⁡min⁡wLtrain(w,α)\begin{aligned} \min_{\alpha} \quad & \mathcal{L}{\text{val}}(w^*(\alpha), \alpha) \\ \text{s.t.} \quad & w^*(\alpha) = \arg\min{w} \mathcal{L}_{\text{train}}(w, \alpha) \end{aligned}αmins.t.Lval(w∗(α),α)w∗(α)=argwminLtrain(w,α)

其中α\alphaα是架构参数，www是权重参数。

通过梯度下降同时优化架构和权重：

∇αLval(w∗(α),α)≈∇αLval(w−ξ∇wLtrain(w,α),α)\nabla_{\alpha} \mathcal{L}{\text{val}}(w^*(\alpha), \alpha) \approx \nabla{\alpha} \mathcal{L}{\text{val}}(w - \xi\nabla_w \mathcal{L}{\text{train}}(w, \alpha), \alpha)∇αLval(w∗(α),α)≈∇αLval(w−ξ∇wLtrain(w,α),α)

这种方法可以自动发现适合特定硬件约束的最优架构。

11.2 联邦学习的潜在应用

Edge Impulse可以扩展支持联邦学习，使多个边缘设备协同训练模型而不共享原始数据。联邦平均算法：

wt+1=∑k=1Knkn⋅wt+1kw_{t+1} = \sum_{k=1}^{K} \frac{n_k}{n} \cdot w_{t+1}^kwt+1=k=1∑Knnk⋅wt+1k

其中wkw_kwk是第kkk个设备的本地模型，nkn_knk是其数据量，nnn是总数据量。

这种方法特别适合隐私敏感的应用，如医疗设备和个人健康监测。

附录：数学推导

A. 快速傅里叶变换

离散傅里叶变换（DFT）的定义：

X[k]=∑n=0N−1x[n]⋅WNknX[k] = \sum_{n=0}^{N-1} x[n] \cdot W_N^{kn}X[k]=n=0∑N−1x[n]⋅WNkn

其中WN=e−j2π/NW_N = e^{-j2\pi/N}WN=e−j2π/N是旋转因子。

Cooley-Tukey FFT算法通过分解实现加速。设N=2mN = 2^mN=2m，将输入序列分为偶数和奇数索引：

X[k]=∑r=0N/2−1x[2r]⋅WN2rk+∑r=0N/2−1x[2r+1]⋅WN(2r+1)k=∑r=0N/2−1x[2r]⋅WN/2rk+WNk⋅∑r=0N/2−1x[2r+1]⋅WN/2rk=Xeven[k]+WNk⋅Xodd[k]\begin{aligned} X[k] &= \sum_{r=0}^{N/2-1} x[2r] \cdot W_N^{2rk} + \sum_{r=0}^{N/2-1} x[2r+1] \cdot W_N^{(2r+1)k} \\ &= \sum_{r=0}^{N/2-1} x[2r] \cdot W_{N/2}^{rk} + W_N^k \cdot \sum_{r=0}^{N/2-1} x[2r+1] \cdot W_{N/2}^{rk} \\ &= X_{\text{even}}[k] + W_N^k \cdot X_{\text{odd}}[k] \end{aligned}X[k]=r=0∑N/2−1x[2r]⋅WN2rk+r=0∑N/2−1x[2r+1]⋅WN(2r+1)k=r=0∑N/2−1x[2r]⋅WN/2rk+WNk⋅r=0∑N/2−1x[2r+1]⋅WN/2rk=Xeven[k]+WNk⋅Xodd[k]

递归关系：

{X[k]=Xeven[k mod N/2]+WNk⋅Xodd[k mod N/2],k<N/2X[k]=Xeven[k mod N/2]−WNk−N/2⋅Xodd[k mod N/2],k≥N/2\begin{cases} X[k] = X_{\text{even}}[k \bmod N/2] + W_N^k \cdot X_{\text{odd}}[k \bmod N/2], & k < N/2 \\ X[k] = X_{\text{even}}[k \bmod N/2] - W_N^{k-N/2} \cdot X_{\text{odd}}[k \bmod N/2], & k \geq N/2 \end{cases}{X[k]=Xeven[kmodN/2]+WNk⋅Xodd[kmodN/2],X[k]=Xeven[kmodN/2]−WNk−N/2⋅Xodd[kmodN/2],k<N/2k≥N/2

计算复杂度分析：

T(N)=2T(N/2)+O(N)T(N) = 2T(N/2) + O(N)T(N)=2T(N/2)+O(N)

根据主定理：T(N)=O(Nlog⁡N)T(N) = O(N \log N)T(N)=O(NlogN)

B. 梅尔频率倒谱系数的推导

从线性频率到梅尔频率的映射：

m=2595log⁡10(1+f700)m = 2595 \log_{10}\left(1 + \frac{f}{700}\right)m=2595log10(1+700f)

逆变换：

f=700(10m/2595−1)f = 700\left(10^{m/2595} - 1\right)f=700(10m/2595−1)

梅尔滤波器组的三角滤波器定义：

Hm(k)={0,k<f(m−1)k−f(m−1)f(m)−f(m−1),f(m−1)≤k<f(m)f(m+1)−kf(m+1)−f(m),f(m)≤k<f(m+1)0,k≥f(m+1)H_m(k) = \begin{cases} 0, & k < f(m-1) \\ \frac{k - f(m-1)}{f(m) - f(m-1)}, & f(m-1) \leq k < f(m) \\ \frac{f(m+1) - k}{f(m+1) - f(m)}, & f(m) \leq k < f(m+1) \\ 0, & k \geq f(m+1) \end{cases}Hm(k)=⎩ ⎨ ⎧0,f(m)−f(m−1)k−f(m−1),f(m+1)−f(m)f(m+1)−k,0,k<f(m−1)f(m−1)≤k<f(m)f(m)≤k<f(m+1)k≥f(m+1)

滤波器组输出：

S(m)=∑k=0N/2∣X(k)∣2⋅Hm(k)S(m) = \sum_{k=0}^{N/2} |X(k)|^2 \cdot H_m(k)S(m)=k=0∑N/2∣X(k)∣2⋅Hm(k)

取对数并应用DCT：

c(n)=2M∑m=1Mlog⁡(S(m))⋅cos⁡(πn(m−0.5)M)c(n) = \sqrt{\frac{2}{M}} \sum_{m=1}^{M} \log(S(m)) \cdot \cos\left(\frac{\pi n(m-0.5)}{M}\right)c(n)=M2 m=1∑Mlog(S(m))⋅cos(Mπn(m−0.5))

其中n=0,1,...,L−1n = 0, 1, \ldots, L-1n=0,1,...,L−1，LLL是所需的MFCC系数数量。

C. 贝叶斯优化的数学框架

高斯过程回归模型：

给定训练数据D={(θi,yi)}i=1n\mathcal{D} = \{(\theta_i, y_i)\}_{i=1}^nD={(θi,yi)}i=1n，后验分布为：

p(f∣D)=N(μn(θ),σn2(θ))p(f|\mathcal{D}) = \mathcal{N}(\mu_n(\theta), \sigma_n^2(\theta))p(f∣D)=N(μn(θ),σn2(θ))

其中：

μn(θ)=k(θ)T(K+σ2I)−1y\mu_n(\theta) = \mathbf{k}(\theta)^T(\mathbf{K} + \sigma^2\mathbf{I})^{-1}\mathbf{y}μn(θ)=k(θ)T(K+σ2I)−1y

σn2(θ)=k(θ,θ)−k(θ)T(K+σ2I)−1k(θ)\sigma_n^2(\theta) = k(\theta, \theta) - \mathbf{k}(\theta)^T(\mathbf{K} + \sigma^2\mathbf{I})^{-1}\mathbf{k}(\theta)σn2(θ)=k(θ,θ)−k(θ)T(K+σ2I)−1k(θ)

k(θ)=[k(θ,θ1),...,k(θ,θn)]T\mathbf{k}(\theta) = [k(\theta, \theta_1), \ldots, k(\theta, \theta_n)]^Tk(θ)=[k(θ,θ1),...,k(θ,θn)]T

Kij=k(θi,θj)K_{ij} = k(\theta_i, \theta_j)Kij=k(θi,θj)

常用的核函数（RBF核）：

k(θ,θ′)=σf2⋅exp⁡(−12l2∥θ−θ′∥2)k(\theta, \theta') = \sigma_f^2 \cdot \exp\left(-\frac{1}{2l^2}\|\theta - \theta'\|^2\right)k(θ,θ′)=σf2⋅exp(−2l21∥θ−θ′∥2)

期望改进（EI）采集函数：

EI(θ)={(μn(θ)−f∗−ξ)Φ(Z)+σn(θ)ϕ(Z),σn(θ)>00,σn(θ)=0\text{EI}(\theta) = \begin{cases} (\mu_n(\theta) - f^* - \xi)\Phi(Z) + \sigma_n(\theta)\phi(Z), & \sigma_n(\theta) > 0 \\ 0, & \sigma_n(\theta) = 0 \end{cases}EI(θ)={(μn(θ)−f∗−ξ)Φ(Z)+σn(θ)ϕ(Z),0,σn(θ)>0σn(θ)=0

其中：

Z=μn(θ)−f∗−ξσn(θ)Z = \frac{\mu_n(\theta) - f^* - \xi}{\sigma_n(\theta)}Z=σn(θ)μn(θ)−f∗−ξ

Φ\PhiΦ是标准正态分布的累积分布函数，ϕ\phiϕ是标准正态分布的概率密度函数，f∗f^*f∗是当前最佳观察值，ξ\xiξ是探索-利用平衡参数。

D. 量化感知训练的梯度计算

前向传播中的量化：

q=Q(r)=s⋅clamp(round(rs),−2b−1,2b−1−1)q = Q(r) = s \cdot \text{clamp}\left(\text{round}\left(\frac{r}{s}\right), -2^{b-1}, 2^{b-1}-1\right)q=Q(r)=s⋅clamp(round(sr),−2b−1,2b−1−1)

直通估计器（STE）用于反向传播：

∂L∂r=∂L∂q⋅1∣r∣≤α\frac{\partial \mathcal{L}}{\partial r} = \frac{\partial \mathcal{L}}{\partial q} \cdot \mathbb{1}_{|r| \leq \alpha}∂r∂L=∂q∂L⋅1∣r∣≤α

其中1∣r∣≤α\mathbb{1}_{|r| \leq \alpha}1∣r∣≤α是指示函数，α\alphaα是截断阈值。

量化感知训练的损失函数：

LQAT=Ltask(fQ(x;θQ))+λ⋅R(θQ)\mathcal{L}{\text{QAT}} = \mathcal{L}{\text{task}}(f_Q(x; \theta_Q)) + \lambda \cdot R(\theta_Q)LQAT=Ltask(fQ(x;θQ))+λ⋅R(θQ)

其中fQf_QfQ是量化网络，RRR是正则化项：

R(θQ)=∑l∥Wl−Q(Wl)∥F2R(\theta_Q) = \sum_l \|W_l - Q(W_l)\|_F^2R(θQ)=l∑∥Wl−Q(Wl)∥F2

梯度更新：

θt+1=θt−η⋅(∇θLtask+λ⋅∇θR)\theta_{t+1} = \theta_t - \eta \cdot (\nabla_{\theta}\mathcal{L}{\text{task}} + \lambda \cdot \nabla{\theta}R)θt+1=θt−η⋅(∇θLtask+λ⋅∇θR)

E. 卡尔曼滤波器的完整推导

状态空间模型：

xk=Fkxk−1+Bkuk+wkzk=Hkxk+vk\begin{aligned} \mathbf{x}_k &= \mathbf{F}k\mathbf{x}{k-1} + \mathbf{B}_k\mathbf{u}_k + \mathbf{w}_k \\ \mathbf{z}_k &= \mathbf{H}_k\mathbf{x}_k + \mathbf{v}_k \end{aligned}xkzk=Fkxk−1+Bkuk+wk=Hkxk+vk

其中：

wk∼N(0,Qk)\mathbf{w}_k \sim \mathcal{N}(0, \mathbf{Q}_k)wk∼N(0,Qk)：过程噪声
vk∼N(0,Rk)\mathbf{v}_k \sim \mathcal{N}(0, \mathbf{R}_k)vk∼N(0,Rk)：观测噪声

预测步骤：

先验状态估计：

x^k−=Fkx^k−1+Bkuk\hat{\mathbf{x}}_k^- = \mathbf{F}k\hat{\mathbf{x}}{k-1} + \mathbf{B}_k\mathbf{u}_kx^k−=Fkx^k−1+Bkuk

先验误差协方差：

Pk−=FkPk−1FkT+Qk\mathbf{P}_k^- = \mathbf{F}k\mathbf{P}{k-1}\mathbf{F}_k^T + \mathbf{Q}_kPk−=FkPk−1FkT+Qk

更新步骤：

卡尔曼增益：

Kk=Pk−HkT(HkPk−HkT+Rk)−1\mathbf{K}_k = \mathbf{P}_k^-\mathbf{H}_k^T(\mathbf{H}_k\mathbf{P}_k^-\mathbf{H}_k^T + \mathbf{R}_k)^{-1}Kk=Pk−HkT(HkPk−HkT+Rk)−1

后验状态估计：

x^k=x^k−+Kk(zk−Hkx^k−)\hat{\mathbf{x}}_k = \hat{\mathbf{x}}_k^- + \mathbf{K}_k(\mathbf{z}_k - \mathbf{H}_k\hat{\mathbf{x}}_k^-)x^k=x^k−+Kk(zk−Hkx^k−)

后验误差协方差：

Pk=(I−KkHk)Pk−\mathbf{P}_k = (\mathbf{I} - \mathbf{K}_k\mathbf{H}_k)\mathbf{P}_k^-Pk=(I−KkHk)Pk−

Joseph形式（数值稳定）：

Pk=(I−KkHk)Pk−(I−KkHk)T+KkRkKkT\mathbf{P}_k = (\mathbf{I} - \mathbf{K}_k\mathbf{H}_k)\mathbf{P}_k^-(\mathbf{I} - \mathbf{K}_k\mathbf{H}_k)^T + \mathbf{K}_k\mathbf{R}_k\mathbf{K}_k^TPk=(I−KkHk)Pk−(I−KkHk)T+KkRkKkT

F. 多目标优化的Pareto前沿计算

ε\varepsilonε-约束方法：

将多目标问题转化为一系列单目标问题：

minimizef1(x)subject tofi(x)≤εi,i=2,...,mx∈X\begin{aligned} \text{minimize} \quad & f_1(x) \\ \text{subject to} \quad & f_i(x) \leq \varepsilon_i, \quad i = 2, \ldots, m \\ & x \in \mathcal{X} \end{aligned}minimizesubject tof1(x)fi(x)≤εi,i=2,...,mx∈X

通过变化ε\varepsilonε值获得Pareto前沿的不同点。

加权和方法的梯度：

∇fws=∑iwi∇fi(x)\nabla f_{\text{ws}} = \sum_i w_i \nabla f_i(x)∇fws=i∑wi∇fi(x)

法向量边界交叉（NBI）方法：

计算锚点：xi∗=arg⁡min⁡fi(x)x_i^* = \arg\min f_i(x)xi∗=argminfi(x)
构造凸包：CH=conv{f(x1∗),...,f(xm∗)}\text{CH} = \text{conv}\{f(x_1^*), \ldots, f(x_m^*)\}CH=conv{f(x1∗),...,f(xm∗)}
生成均匀分布的权重向量
对每个权重向量，求解子问题：

maximizetsubject toΦw+t⋅n^=f(x)x∈X\begin{aligned} \text{maximize} \quad & t \\ \text{subject to} \quad & \Phi w + t \cdot \hat{n} = f(x) \\ & x \in \mathcal{X} \end{aligned}maximizesubject totΦw+t⋅n^=f(x)x∈X

其中Φ\PhiΦ是支付矩阵，n^\hat{n}n^是法向量。

G. 神经网络压缩的奇异值分解

对于全连接层权重矩阵W∈Rm×n\mathbf{W} \in \mathbb{R}^{m \times n}W∈Rm×n，SVD分解：

W=UΣVT=∑i=1rσiuiviT\mathbf{W} = \mathbf{U}\mathbf{\Sigma}\mathbf{V}^T = \sum_{i=1}^r \sigma_i \mathbf{u}_i \mathbf{v}_i^TW=UΣVT=i=1∑rσiuiviT

低秩近似（保留kkk个最大奇异值）：

W~=∑i=1kσiuiviT\tilde{\mathbf{W}} = \sum_{i=1}^k \sigma_i \mathbf{u}_i \mathbf{v}_i^TW~=i=1∑kσiuiviT

近似误差（Frobenius范数）：

∥W−W~∥F=∑i=k+1rσi2\|\mathbf{W} - \tilde{\mathbf{W}}\|F = \sqrt{\sum{i=k+1}^r \sigma_i^2}∥W−W~∥F=i=k+1∑rσi2

压缩率：

CR=mnk(m+n+1)\text{CR} = \frac{mn}{k(m+n+1)}CR=k(m+n+1)mn

相对误差界：

∥W−W~∥F∥W∥F≤∑i=k+1rσi2∑i=1rσi2\frac{\|\mathbf{W} - \tilde{\mathbf{W}}\|F}{\|\mathbf{W}\|F} \leq \frac{\sqrt{\sum{i=k+1}^r \sigma_i^2}}{\sqrt{\sum{i=1}^r \sigma_i^2}}∥W∥F∥W−W~∥F≤∑i=1rσi2 ∑i=k+1rσi2

H. 网络剪枝的理论基础

结构化剪枝的优化问题：

min⁡L(W⊙M)+λ∥M∥0\min \mathcal{L}(\mathbf{W} \odot \mathbf{M}) + \lambda\|\mathbf{M}\|_0minL(W⊙M)+λ∥M∥0

其中M\mathbf{M}M是二进制掩码，⊙\odot⊙是逐元素乘积，∥⋅∥0\|\cdot\|_0∥⋅∥0是L0范数。

由于L0范数不可微，使用L1松弛：

min⁡L(W⊙M)+λ∥W∥1\min \mathcal{L}(\mathbf{W} \odot \mathbf{M}) + \lambda\|\mathbf{W}\|_1minL(W⊙M)+λ∥W∥1

迭代幅度剪枝（IMP）算法：

训练网络至收敛：W∗=arg⁡min⁡L(W)\mathbf{W}^* = \arg\min \mathcal{L}(\mathbf{W})W∗=argminL(W)
剪枝p%p\%p%最小权重：M=1∣W∗∣>τp\mathbf{M} = \mathbb{1}_{|\mathbf{W}^*| > \tau_p}M=1∣W∗∣>τp
重新初始化并训练：W′=W0⊙M\mathbf{W}' = \mathbf{W}_0 \odot \mathbf{M}W′=W0⊙M
重复直到达到目标稀疏度

彩票假设的数学表述：

存在子网络(M,W0⊙M)(\mathbf{M}, \mathbf{W}_0 \odot \mathbf{M})(M,W0⊙M)，使得：

L(f(x;W0⊙M,t))≤L(f(x;W∗,T))\mathcal{L}(f(x; \mathbf{W}_0 \odot \mathbf{M}, t)) \leq \mathcal{L}(f(x; \mathbf{W}^*, T))L(f(x;W0⊙M,t))≤L(f(x;W∗,T))

其中t≪Tt \ll Tt≪T是训练迭代次数。