Day 26 常见的降维算法

特征降维是机器学习中的关键预处理步骤，核心目标是 在保留数据核心信息的前提下，减少特征维度------ 解决高维数据的 "维度灾难"（如计算量大、过拟合风险高、模型可解释性差），同时提升模型训练效率与泛化能力。

一、为什么需要特征降维？

高维数据（如特征数＞100）会带来以下问题：

计算成本高：特征越多，模型训练 / 推理时间越长，硬件资源消耗越大；
过拟合风险：高维空间中数据稀疏，模型易 "死记硬背" 训练数据噪声，导致泛化能力差；
可解释性差：过多特征难以区分核心影响因素（如回归任务中，无法判断哪个特征对房价影响最大）；
数据冗余：部分特征可能高度相关（如 "身高" 与 "体重"、"RMSE" 与 "MSE"），重复携带信息。

降维的核心价值：去冗余、提效率、稳泛化、易解释，且不显著损失模型性能。

二、特征降维的核心分类

根据是否利用 "目标变量信息"，降维方法分为两大类：

类型	核心特点	代表方法	适用场景
无监督降维（Unsupervised）	不依赖目标变量（y），仅基于特征矩阵（X）的分布降维	PCA、SVD、t-SNE、UMAP、LLE	探索性数据分析、无标签数据、分类 / 回归通用
有监督降维（Supervised）	利用目标变量（y）的信息，优先保留对 y 区分 / 预测有用的特征	LDA、Fisher 判别分析、 ReliefF	有标签数据、分类任务为主（LDA 适配分类，回归需调整）
特征选择（Subset Selection）	直接筛选 "重要特征子集"，而非重构特征（降维后仍为原始特征）	方差筛选、相关性筛选、递归特征消除（RFE）	需保留原始特征含义、可解释性要求高的场景

注：常说的 "降维" 多特指「特征变换类方法」（如 PCA、LDA），但特征选择是更直接的 "降维思路"，一并纳入讲解。

三、主流降维方法

（一）无监督降维方法（最常用）

1. PCA（主成分分析）------ 线性降维首选

核心原理

找到数据中 "方差最大的正交方向"（主成分），将原始特征投影到这些主成分上，形成新的低维特征；
核心假设：方差越大的方向，包含的信息越多；
降维后特征是原始特征的线性组合（如 PC1 = 0.8× 收入 + 0.2× 房屋年龄）。

优缺点

✅ 优点：计算高效、线性可解释、无参数、广泛适配各类数据；
❌ 缺点：仅保留方差大的特征（可能丢失对目标变量重要但方差小的信息）、对非线性数据效果差、敏感于特征尺度（需先标准化）。

适用场景

高维线性数据（如特征数＞50）、分类 / 回归任务通用、追求高效降维；
示例：加州房价回归（8 维特征→2-3 维主成分）、图像数据降维（像素矩阵→低维特征）。

实现代码（适配回归任务）

复制代码

import numpy as np
import pandas as pd
from sklearn.decomposition import PCA
from sklearn.preprocessing import StandardScaler

# 前提：已完成数据预处理（X_train_scaled：标准化后的训练集特征）
# PCA需先标准化（特征尺度一致）
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)

# 1. 初始化PCA，指定降维后维度（或按方差占比自动选择）
# 方式1：指定维度（如降为2维）
pca = PCA(n_components=2, random_state=42)
# 方式2：按方差占比（如保留95%的信息）
# pca = PCA(n_components=0.95, random_state=42)

# 2. 拟合+降维（无监督：仅用X，不用y）
X_train_pca = pca.fit_transform(X_train_scaled)
X_test_pca = pca.transform(scaler.transform(X_test))  # 测试集用训练集scaler标准化

# 3. 查看结果
print(f"PCA降维前：{X_train_scaled.shape}")  # (16512, 8)
print(f"PCA降维后：{X_train_pca.shape}")    # (16512, 2)
print(f"各主成分方差占比：{pca.explained_variance_ratio_}")  # 如[0.65, 0.20]（共保留85%信息）
print(f"累计方差占比：{pca.explained_variance_ratio_.sum():.2f}")  # 确保信息保留充足

2. SVD（奇异值分解）------ 与 PCA 等价，适配稀疏数据

核心原理

对特征矩阵 X 做奇异值分解：X=UΣVT，其中VT的前 k 行即为降维后的投影矩阵；
与 PCA 的关系：当 X 标准化后，SVD 的主成分与 PCA 完全一致，但 SVD 无需计算协方差矩阵，更适合稀疏数据（如文本 TF-IDF 矩阵）。

优缺点

✅ 优点：兼容稀疏数据、计算稳定（避免协方差矩阵奇异）、与 PCA 效果一致；
❌ 缺点：同 PCA（线性降维、敏感于尺度）。

适用场景

稀疏高维数据（如文本、推荐系统）、与 PCA 适用场景重叠，优先选 SVD 处理稀疏数据。

实现代码

复制代码

from sklearn.decomposition import TruncatedSVD  # 截断SVD（高效处理大规模数据）

svd = TruncatedSVD(n_components=2, random_state=42)
X_train_svd = svd.fit_transform(X_train_scaled)
X_test_svd = svd.transform(scaler.transform(X_test))

print(f"SVD降维后：{X_train_svd.shape}")
print(f"累计方差占比：{svd.explained_variance_ratio_.sum():.2f}")

3. t-SNE ------ 非线性降维（可视化首选）

核心原理

基于 "概率分布匹配"：先将高维数据中样本的 "欧氏距离" 转化为 "相似度概率"，再在低维空间中构建相同的概率分布，实现非线性降维；
核心优势：能捕捉数据的非线性结构（如聚类、流形），降维后可视化效果极佳。

优缺点

✅ 优点：非线性降维效果好、可视化友好（适合 2D/3D 展示）、能发现数据聚类结构；
❌ 缺点：计算量大（不适合百万级样本）、训练时间长、对参数（perplexity）敏感、不适合直接用于建模（仅适合可视化）。

适用场景

高维数据可视化（如将 100 维特征降为 2D 画图）、探索数据聚类结构（如判断样本是否有明显类别划分）。

实现代码（可视化示例）

复制代码

from sklearn.manifold import TSNE
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei']

# t-SNE降维（通常降为2D用于可视化）
tsne = TSNE(n_components=2, perplexity=30, random_state=42)
X_train_tsne = tsne.fit_transform(X_train_scaled)

# 可视化（假设y_train是类别标签或回归目标值）
plt.figure(figsize=(8, 6))
scatter = plt.scatter(X_train_tsne[:, 0], X_train_tsne[:, 1], c=y_train, cmap='viridis', alpha=0.6)
plt.colorbar(scatter, label='目标变量（如房价）')
plt.title('t-SNE降维可视化（2D）')
plt.xlabel('TSNE1')
plt.ylabel('TSNE2')
plt.show()

4. UMAP ------ 非线性降维（t-SNE 的高效替代）

核心原理

基于 "流形学习"：假设高维数据分布在低维流形上，通过保留样本的 "局部邻域关系" 实现降维；
对比 t-SNE：计算速度快 10-100 倍，支持大规模数据，且能更好保留全局结构。

优缺点

✅ 优点：非线性效果好、计算高效、兼顾局部与全局结构、支持可视化与建模；
❌ 缺点：对参数（n_neighbors）敏感、需安装额外库（umap-learn）。

适用场景

大规模非线性数据降维（如 10 万级样本）、可视化 + 建模双重需求（降维后可直接用于训练模型）。

实现代码

复制代码

# 先安装：pip install umap-learn
import umap

umap_model = umap.UMAP(n_components=2, n_neighbors=15, random_state=42)
X_train_umap = umap_model.fit_transform(X_train_scaled)
X_test_umap = umap_model.transform(scaler.transform(X_test))

# 可视化
plt.figure(figsize=(8, 6))
plt.scatter(X_train_umap[:, 0], X_train_umap[:, 1], c=y_train, cmap='viridis', alpha=0.6)
plt.title('UMAP降维可视化')
plt.show()

（二）有监督降维方法

5. LDA（线性判别分析）------ 分类任务首选

核心原理

有监督降维：利用目标变量 y 的信息，找到 "最大化类别间距离、最小化类别内距离" 的投影方向；
数学约束：降维后维度最大为「类别数 - 1」（如 3 类数据最多降为 2 维）；
关键区别于 PCA：PCA 仅关注 X 的方差，LDA 关注 X 与 y 的关联（更适合分类）。

优缺点

✅ 优点：分类任务降维效果优于 PCA、能强化类别区分度、降低过拟合风险；
❌ 缺点：仅适用于分类任务（回归任务无 "类别" 概念，无法直接用）、对异常值敏感、线性降维（不适合非线性数据）。

适用场景

有标签分类数据（如图片分类、疾病诊断）、希望降维后直接提升分类准确率的场景。

实现代码（分类任务）

复制代码

from sklearn.discriminant_analysis import LinearDiscriminantAnalysis as LDA

# 前提：y_train是分类标签（如0/1/2）
lda = LDA(n_components=min(2, len(np.unique(y_train))-1))  # 遵循LDA维度约束
X_train_lda = lda.fit_transform(X_train_scaled, y_train)  # 有监督：需传入y_train
X_test_lda = lda.transform(scaler.transform(X_test))

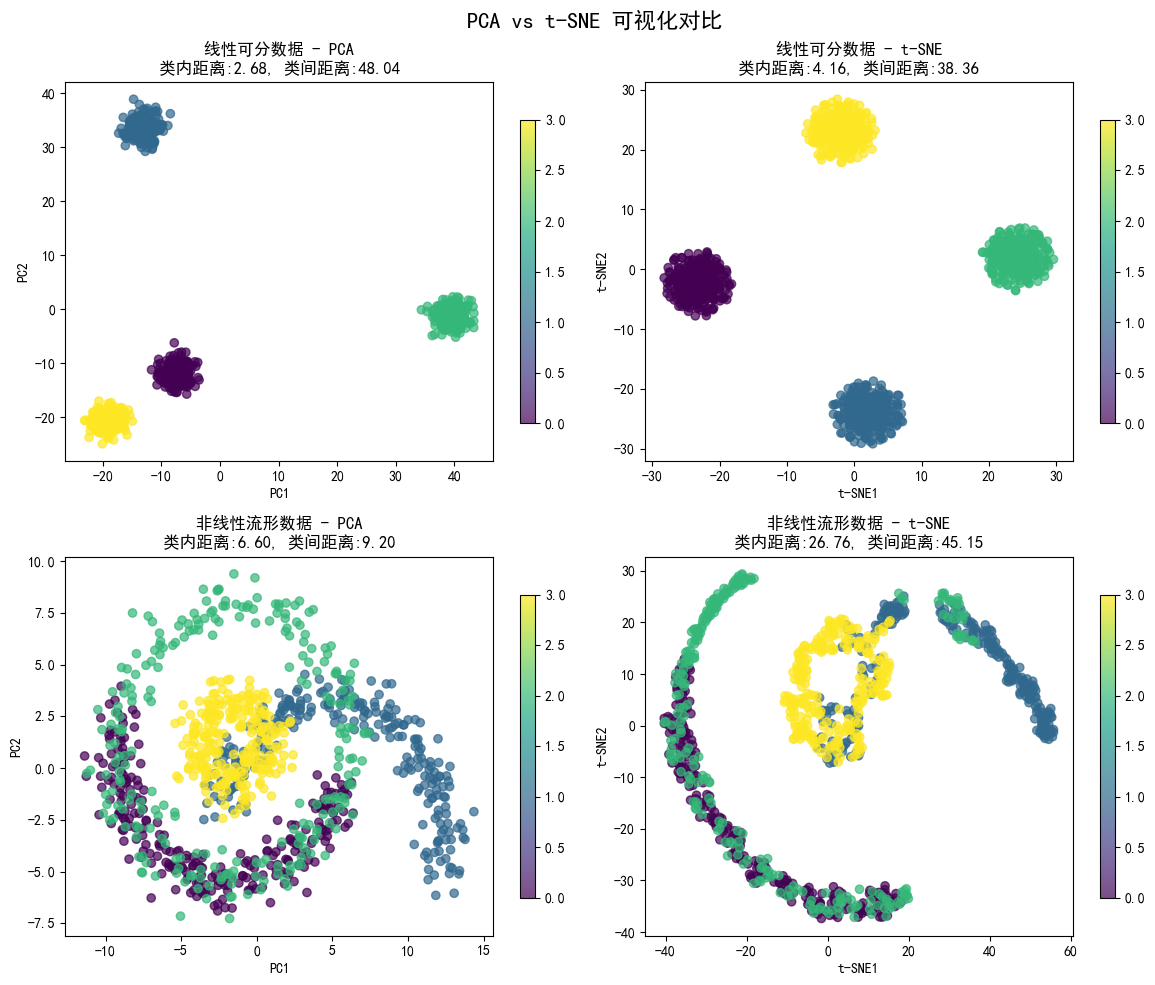
print(f"LDA降维后：{X_train_lda.shape}")  # 如(1000, 2)（3类数据）

四、PCA 与 t-SNE 可视化核心区别总结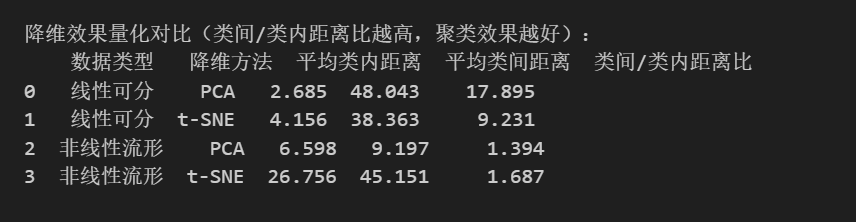

对比维度	PCA（线性降维）	t-SNE（非线性降维）
核心原理	保留数据方差最大的线性方向（主成分）	匹配高维与低维空间的概率分布（保留局部邻域）
适用数据类型	线性可分、低维冗余数据	非线性流形、复杂聚类数据（如环形、螺旋形）
可视化效果	线性结构清晰，非线性结构无法还原	非线性结构还原度极高，聚类分离更明显
计算速度	极快（O (n×d²)，n = 样本数，d = 特征数）	较慢（O (n²)，样本＞1 万时需优化）
全局结构保留	好（能反映数据整体分布）	差（过度关注局部，可能扭曲全局结构）
参数敏感性	无参数（仅需指定维度）	敏感（perplexity、learning_rate 影响大）
信息保留逻辑	保留 "全局方差最大" 的信息	保留 "局部邻域相似性" 的信息
典型应用场景	高维线性数据可视化、快速降维探索	非线性数据聚类探索、复杂数据分布可视化