点击下面查看作者专栏 🔥🔥C语言专栏🔥🔥 🌊🌊编程百度🌊🌊 🌠🌠如何获取自己的代码仓库🌠🌠
🌐索引与导读
- 暴力枚举(BF)的概念
- 暴力枚举的算法步骤
- 例题讲解
-
- 经典案例讲解一:百鸡问题
- 经典案例讲解二:盛最多水的容器
- 经典案例讲解三:两数之和
- 经典案例讲解四:2025
-
- [💻 代码实现](#💻 代码实现)
- 希望读者多多三连
- 给小编一些动力
- 蟹蟹啦!
暴力枚举(BF)的概念
暴力枚举也称为穷举法,是计算机算法中最基础、最直观,但也是最费劲的一种解题思路
像我们平时没有最优解的算法题,往往都可以通过暴力枚举去算出最终结果
- 核心思想
不靠巧妙的技巧,而是利用计算机强大的计算能力,把所有可能的情况列举出来,一个一个去验证,直到找到正确答案
暴力枚举的算法步骤
- 列举 :确定解空间的范围,列出所有可能的解候选者
- 检验 :对每一个候选者进行判断,看它是否满足题目条件
例题讲解
下面我们通过几道算法题来感受暴力拆解的快感💪💪 💥 💥
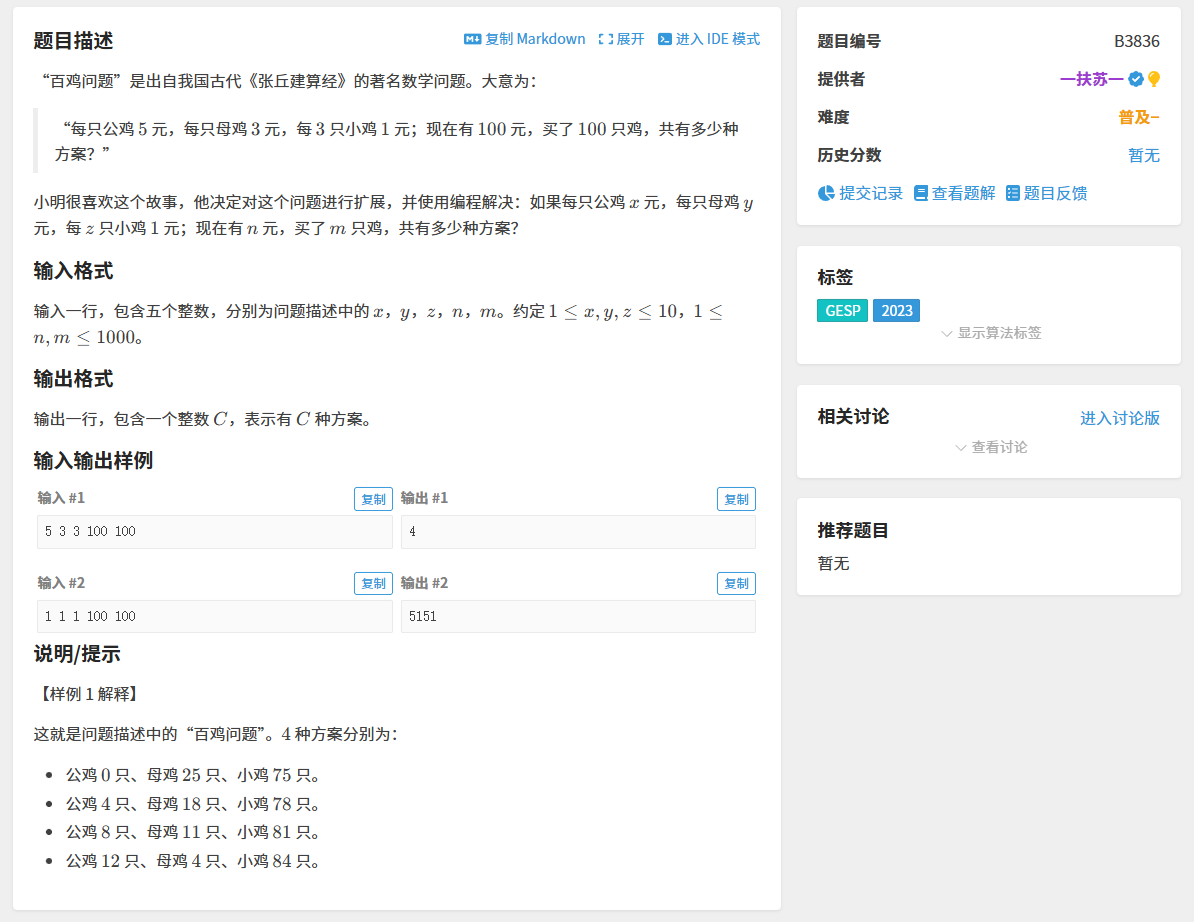
经典案例讲解一:百鸡问题
题目解析
我们要解决的核心问题是找到三个未知数 (公鸡数量、母鸡数量、小鸡数量)
- 假设:
- 公鸡数量为 i i i
- 母鸡数量为 j j j
- 小鸡数量为 k k k
- 必须满足的两个等式:
- 数量守恒: i + j + k = m i + j + k = m i+j+k=m (鸡的总数是 m m m)
- 价格守恒: i × x + j × y + k z = n i \times x + j \times y + \frac{k}{z} = n i×x+j×y+zk=n (总花费是 n n n)
- 隐含条件:
- k k k 必须能被 z z z 整除(因为题目说 z z z 只小鸡 1 元,如果买的小鸡数量不是 z z z 的倍数,价格就不是整数,这在古代数学题中通常隐含价格为整数,且代码中 k/z 若不能整除会有精度问题,需特别判断)
- i , j , k i, j, k i,j,k 必须是非负整数。
思路方案
- 方案 A:三层循环
- 写三层 for 循环
- 时间复杂度: O ( m 3 ) O(m^3) O(m3)
c
// ❌ 效率低,不推荐
for (int i = 0; i <= m; i++) { // 第一层:猜公鸡数量
for (int j = 0; j <= m; j++) { // 第二层:猜母鸡数量
for (int k = 0; k <= m; k++) { // 第三层:猜小鸡数量
// 此时我们要检查两个条件:
// 1. 数量够不够 m 只? (i + j + k == m)
// 2. 钱对不对?
if (i + j + k == m && k % z == 0 && (i * x + j * y + k / z == n)) {
count++;
}
}
}
}- 方案 B:两层循环
- 时间复杂度: O ( m 2 ) O(m^2) O(m2)
c
#include <stdio.h>
int main() {
// 定义变量
// x: 公鸡单价, y: 母鸡单价, z: z只小鸡1元
// n: 总钱数, m: 总鸡数
int x, y, z, n, m;
// 读取输入
if (scanf("%d %d %d %d %d", &x, &y, &z, &n, &m) != 5) {
return 1;
}
int count = 0; // 用来记录满足条件的方案总数
// 第一层循环:枚举公鸡数量 i
// 公鸡最多买 m 只(其实也可以优化为 n/x 只,但写 m 不会错且逻辑简单)
for (int i = 0; i <= m; i++) {
// 第二层循环:枚举母鸡数量 j
// 母鸡的数量加上公鸡数量不能超过总数 m
for (int j = 0; j <= m - i; j++) {
// 剩下的就是小鸡数量 k
int k = m - i - j;
// 核心判断逻辑:
// 1. k % z == 0 : 小鸡数量必须是 z 的倍数,否则价格不是整数(题目隐含逻辑)
// 2. 价格公式 : 公鸡钱 + 母鸡钱 + 小鸡钱 == 总钱数 n
if (k % z == 0 && (i * x + j * y + k / z == n)) {
count++; // 如果满足条件,方案数 +1
}
}
}
// 输出结果
printf("%d\n", count);
return 0;
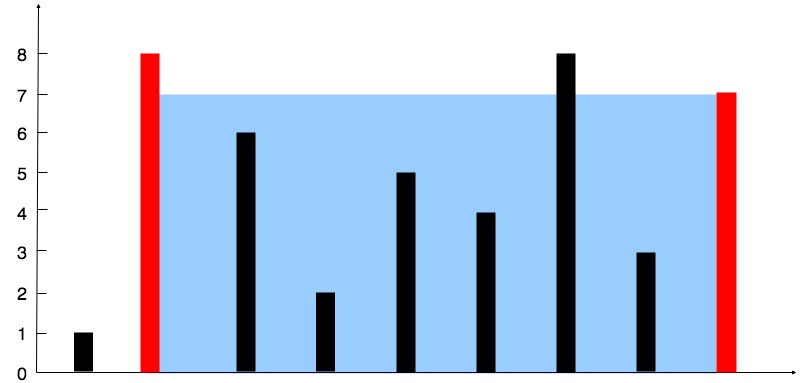
}经典案例讲解二:盛最多水的容器
暴力枚举算法
c
// 辅助函数:求两个数的较小值
int min(int a, int b) {
return a < b ? a : b;
}
int maxArea(int* height, int heightSize) {
int max_water = 0; // 用于记录最大水量
// 外层循环:确定左边界 i
for (int i = 0; i < heightSize - 1; i++) {
// 内层循环:确定右边界 j
for (int j = i + 1; j < heightSize; j++) {
// 1. 计算当前容器的高度(受限于较短的一边)
int current_height = min(height[i], height[j]);
// 2. 计算当前容器的宽度
int current_width = j - i;
// 3. 计算当前面积
int current_area = current_height * current_width;
// 4. 如果当前面积比历史最大值大,则更新
if (current_area > max_water) {
max_water = current_area;
}
}
}
return max_water;
}- 这段代码
又是函数开销,又是双for循环实现的暴力枚举,在比赛中很容易导致超时
所以暴力枚举只要不是没办法,最好慎用!!!
最优解
c
#define MAX(a,b) (a>b?a:b)
#define MIN(a,b) (a<b?a:b)
int maxArea(int* height, int heightSize) {
int ret = 0;
int l = 0; int r = heightSize - 1;
while (l < r) {
int current_height = MIN(height[l], height[r]);
int current_Water = current_height * (r - l);
ret = MAX(ret, current_Water);
if (height[l] < height[r]) {
++l;
}
else {
--r;
}
}
return ret;
}运用#define宏定义 来减少开销,并运用双指针 避免用到双for循环 导致超时
经典案例讲解三:两数之和
解题思路
- 暴力枚举的核心思想
检查数组中每一个可能的数对组合- 外层循环: 使用指针
i从数组的第0个元素遍历到倒数第2个元素 - 内层循环: 使用指针
j从i + 1开始遍历到数组的最后一个元素(这样可以避免重复使用同一个元素,且避免重复检查) - 判断: 如果
nums[i] + nums[j] == target,则说明找到了答案 - 返回: 分配内存并返回包含
i和j的数组
- 外层循环: 使用指针
代码示例
c
int* twoSum(int* nums, int numsSize, int target, int* returnSize) {
// 外层循环:遍历第一个数
for (int i = 0; i < numsSize; i++) {
// 内层循环:遍历第二个数
// j 从 i+1 开始,确保不重复使用元素,也不重复计算
for (int j = i + 1; j < numsSize; j++) {
// 判断两数之和是否等于目标值
if (nums[i] + nums[j] == target) {
// 分配内存用于存储结果(需要存放2个int)
int* result = (int*)malloc(2 * sizeof(int));
// 检查内存分配是否成功
if (result == NULL) {
*returnSize = 0;
return NULL;
}
// 存入下标
result[0] = i;
result[1] = j;
// 设置返回数组的大小为 2
*returnSize = 2;
// 返回结果指针
return result;
}
}
}
}🔥下面罗列出这段代码中需要强调的点🔥
int* result = (int*)malloc(2 * sizeof(int));
text
result → [ int空间 ][ int空间 ]
result[0] result[1]result[0] = i;
result[1] = j;
虽然result是指针,但可以像数组一样使用
result[0]等价于*(result + 0)
result[1]等价于*(result + 1)
数组和指针关系不理解的看下面
Lucy的空间骇客裂缝:数组与指针
经典案例讲解四:2025

这是一个非常经典的暴力枚举(Brute Force) 算法题目
💻 代码实现
c
#include <iostream>
using namespace std;
bool check(int num) {
int c0 = 0, c2 = 0, c5 = 0;
//逐步取出最后一个数字
while (num > 0) {
int my_Function_Num = num % 10;
if (my_Function_Num == 0) {
c0++;
}
else if (my_Function_Num == 2) {
c2++;
}
else if (my_Function_Num == 5) {
c5++;
}
num /= 10;
}
// 条件:至少1个0,2个2,1个5
return (c2 >= 2)&&(c0 >= 1)&&(c5 >= 1);
}
int main() {
//统计满足条件的数的数量
int count = 0;
//检查函数,判断一个数是否满足条件
for (int i = 0; i <= 20250412; i++) {
if (check(i)) {
count++;
}
}
cout << "满足条件的数的数量为:" << count << endl;
return 0;
}希望读者多多三连
给小编一些动力
蟹蟹啦!