一、几何光学的基本定律
几何光学以光线为基本研究对象,研究光的传播和成像规律。其核心定律包括:
1. 光的直线传播定律
- 内容:光在均匀透明介质中沿直线传播。
- 现象:影子形成、日食月食、针孔成像。
- 限制:当光通过小孔或障碍物时,会因衍射现象偏离直线(波动光学范畴)。
2. 光的独立传播定律
- 内容:两束光相遇时互不干扰,各自独立传播;相遇后光能量简单相加。
- 应用:舞台灯光设计、多光源照明系统。
3. 反射定律
- 内容 :
- 反射光线与入射光线、法线在同一平面内。
- 入射角等于反射角(符号规则:入射角为光线与法线的夹角)。
- 特例:平面镜成像遵循反射定律,形成虚像(如镜子中的自己)。
4. 折射定律(斯涅尔定律)
-
内容 :光从一种介质进入另一种介质时,传播方向改变,满足:
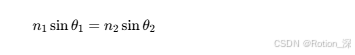
- n1,n2为介质折射率,θ1, θ2 为入射角和折射角。
-
现象:筷子在水中"弯折"、海市蜃楼。
5. 光路可逆性
- 内容:光沿任意路径传播时,正向和逆向路径的光程相等。
- 应用:光纤通信中的光信号传输。
二、成像的基本概念与完善成像条件
1. 物与像的虚实
- 实物:实际发光或被照明的物体(如灯泡、月亮)。
- 虚物:由其他光学系统形成的像被当前系统接收(如显微镜中的标本)。
- 实像:实际光线会聚形成的像(如投影仪屏幕上的图像)。
- 虚像:光线反向延长线会聚形成的像(如平面镜中的像)。
2. 完善成像条件
- 定义:物体上每个点发出的同心光束(球面波),经过光学系统后仍保持同心光束。
- 条件 :
- 入射波面为球面波 → 出射波面也为球面波。
- 物点与像点之间任意两条光路的光程相等(费马原理)。
- 近轴近似 :仅当光线与光轴夹角很小 θ≈sinθ≈tanθ 时成立,此时系统称为高斯光学系统。
三、光学计算与近轴光学系统
1. 近轴光线的特点
- 定义:光线与光轴夹角极小(通常小于5°),可用弧度近似正弦值。
- 优势:简化计算,忽略高阶像差(如球差)。
2. 近轴光学公式
-
物像关系 :

- (l, l'):物距和像距;(r):球面曲率半径。
-
放大率 :


- β:横向放大率;γ:角放大率。
3. 像差
- 球差:轴上点宽光束成像时边缘光线偏离理想位置。
- 色差:不同波长光折射率不同导致的像模糊(如彩虹效应)。
四、球面光学成像系统
1. 单个折射球面成像
-
公式推导 :利用近轴近似,物像关系简化为:

-
放大率:若物体位于球面左侧((l < 0)),则像可能放大或缩小,正立或倒立。
2. 球面反射镜成像
-
公式 :

-
,其中
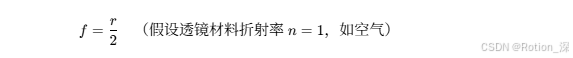
为焦距。
-
特点:
- 物距 (l > 0) 时成实像,(l < 0) 时成虚像。
- 凹面镜汇聚光线,凸面镜发散光线。
3. 共轴球面系统
- 转面公式:光线通过多个球面时,逐面计算物像位置。
- 拉赫不变量:( n u y = n' u' y' ),表征系统传递的光能量和空间信息。
总结
几何光学通过简化光的行为(如直线传播、近轴近似)解决实际问题,但需注意其局限性(如衍射、像差)。成像系统的设计需平衡光路计算与像差校正,例如显微镜通过多透镜组合减少球差。近轴光学是理解复杂光学系统的基础,而球面系统则是实际应用中最常见的模型。