本文是记录专业课计算机图形学的部分笔记,参考教材为Angel的第八版交互式计算机图形学------基于WebGL 2.0的自顶向下方法。
1、几何阶段之后,顶点装配成几何图元,必须对视见体之外的图元进行裁剪(算法是基于顶点表示的图元),找到每个图元所对应的像素,然后产生像素片元、进行光栅化/扫描转换。
2、我们可以考虑绘制由不透明对象构成的场景的两种方法:
①第一种是对于每个像素,确定投影到这个像素的离观察者最近的那个对象,从而基于该对象计算像素的明暗值,这是光线跟踪框架,被称作面向图像(image-oriented)方法,也叫先排序方法。他的优点是任何时刻只需有限的显示内存(仅仅用于存放最后的像素颜色结果),且可以按显示器的刷新速度和次序生成像素;利用相邻像素间的连贯性可设计增量式算法;适合处理全局效果。但缺点是需要复杂的几何对象的数据结构、必须确定哪些图元影响哪些像素,绘制过程中需要随时访问所有的全局几何数据,速度慢;只适合视点相关的静态场景。
②第二种是对于每个对象,确定它所覆盖的像素,并用对象的状态确定像素的明暗值,是一种流水线方法(必须跟踪深度值),被称作面向对象(object-oriented)方法,也叫后排序方法。其优点是处理速度快,运行成本低。缺点是过去需要占用辅助显示内存(例如深度缓存等),每个对象单独处理的代价较大。这个缺点由于低价大容量显示内存、专用硬件芯片的出现,已不再是问题。不过,他还是存在着缺乏全局信息、不能得到大多数全局效果(例如涉及多个对象的复杂光照)的其他问题。在隐藏面消除方法中,Z buffer可以存储有限的全局深度信息。
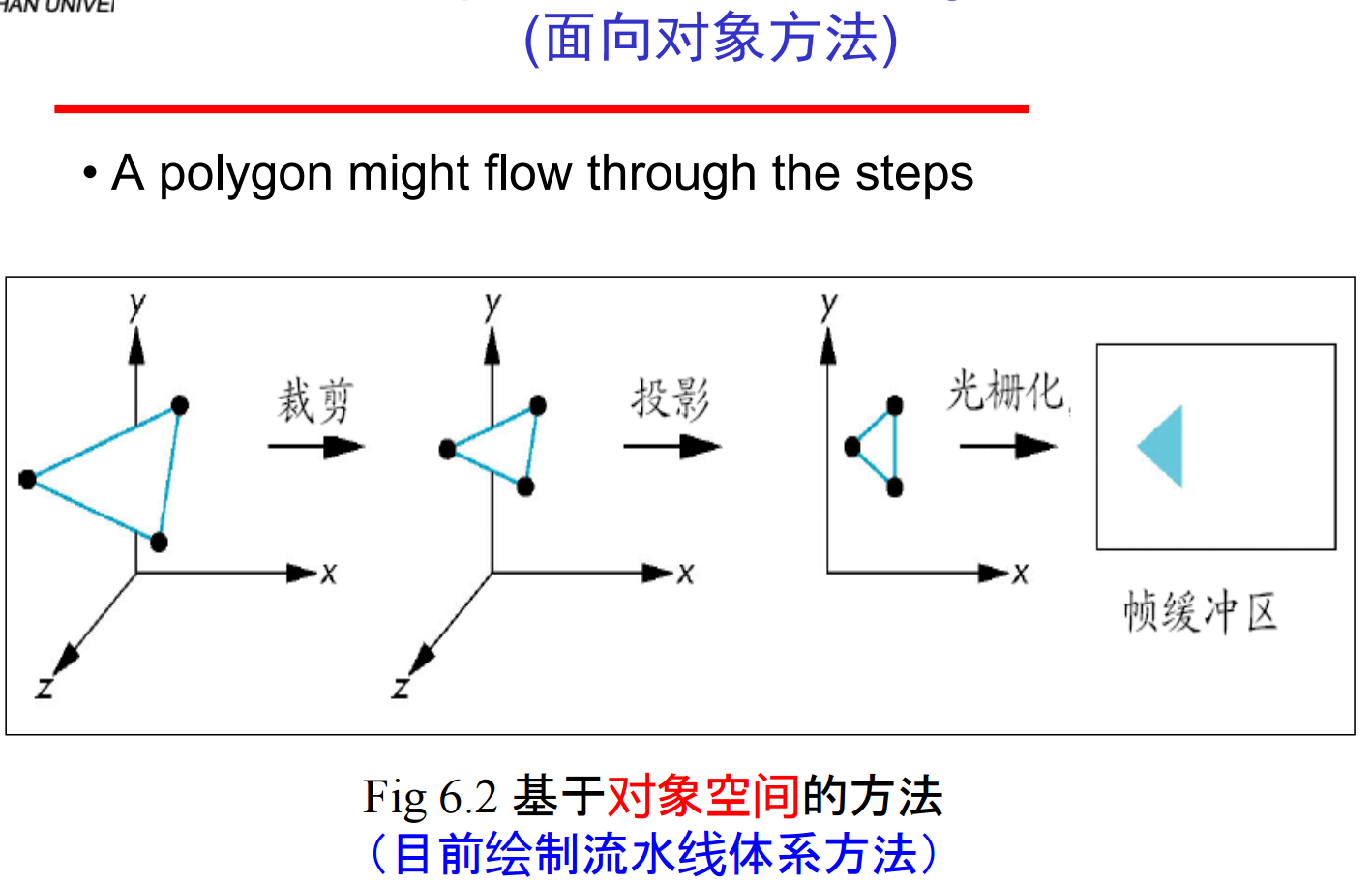
这里的先排序还是后排序是基于隐藏面消除发生的地方进行命名的。
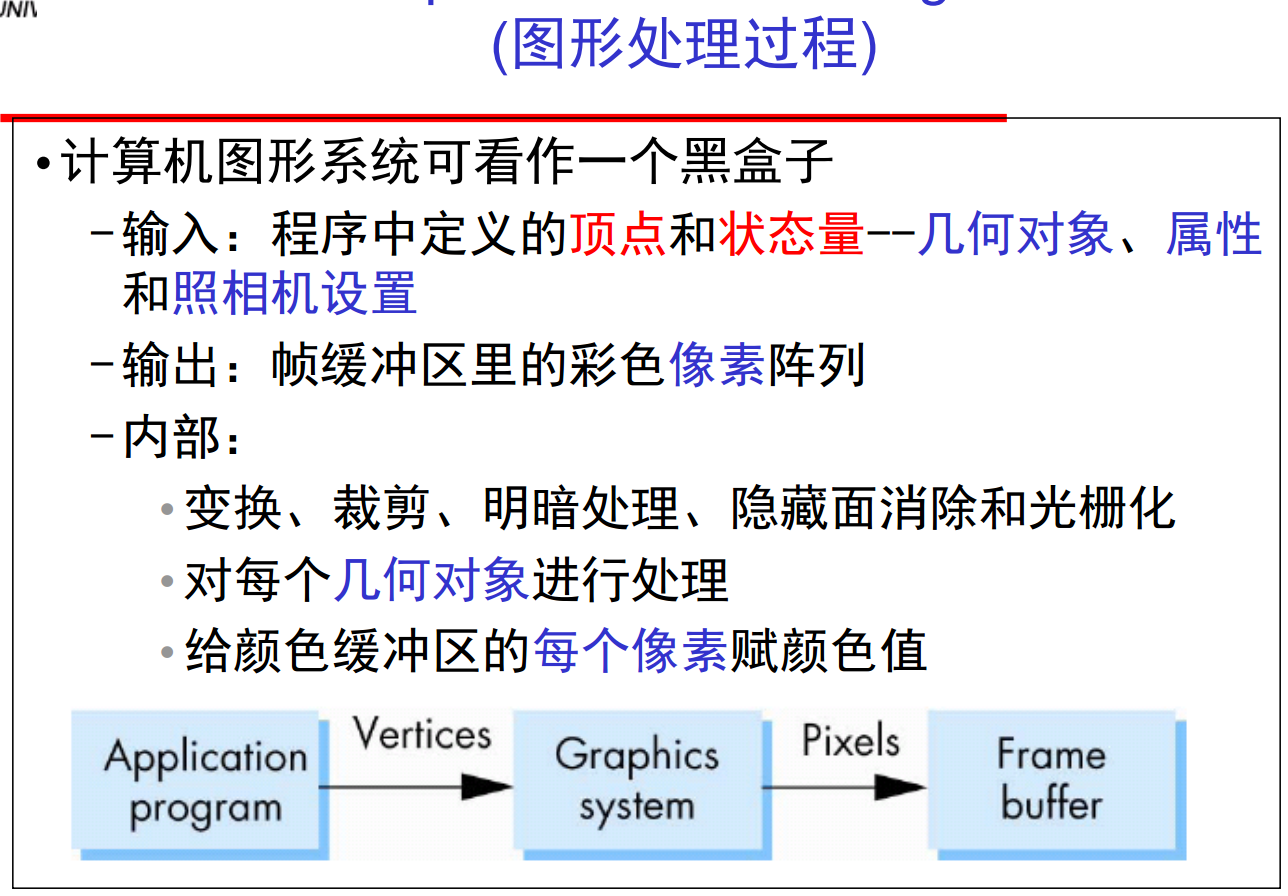
3、图形绘制系统的四个主要任务是:
①Modeling建模。建模器可以认为是一个黑盒子,输出几何对象的顶点数据集,工作在对象坐标系 / 世界坐标。
②Transformations几何处理。几何处理的对象是顶点,目的是确定显示在屏幕上的几何对象,并确定这些对象顶点的颜色值或明暗值。
(1)投影(包括各种坐标变换)。第一步是利用模型-视图变换把几何对象从对象坐标系变换到照相机坐标系或视点坐标系;第二步是利用投影变换把顶点变换到规范化视景体(顶点表示为裁剪坐标)。
(2)图元装配。变换是对顶点进行的,在进行后续操作需要组装成几何对象,称为图元装配(从裁剪角度而言,裁剪是针对图元进行的;从光栅化角度而言,光栅器不能对顶点单独进行处理,而是线段、多边形等图元)。
(3)裁剪。裁剪器确定哪些图元或图元的哪些部分会被传送到光栅器,最终可能会显示在屏幕上。对于完全处在视景体内的图元,经过光栅化后能被显示在屏幕上;对于部分处在视景体内的图元,裁剪后生成新的图元,然后光栅化显示。没被裁剪掉的顶点,仍表示为四维齐次坐标,通过透视除法转换为三维的规范化设备坐标。
(4)光照和明暗处理。就是为每个顶点赋颜色,第一种方法是由当前绘制颜色决定、程序直接指定,第二种方法是开启光照时,根据改进的Phong模型计算得到。
③Rasterization or scan conversion光栅化。这是从裁剪后的对象生成片元(准像素)的过程。对于线段,确定哪些像素可用来近似表示顶点间的线段;对于多边形,确定哪些像素位于多边形顶点定义的二维区域的内部。片元的颜色取决于系统状态值颜色或由光照模型计算的顶点颜色,经过明暗插值算法得到。其输入是由规范化设备坐标表示的顶点,输出由二维窗口坐标表示的片元
④Fragments Processing片元处理。最简单的情形下片元的颜色由光栅器赋值,并且该值就是片元所对应的帧缓冲区中像素的颜色值。但有些任务会被推迟到这个步骤中,比如隐藏面消除(确定可见对象的片元值,这里的可见对象指位于视景体内、且没有被其他更靠近照相机的不透明对象所遮挡的对象)、纹理贴图(像素流水线)、融合(半透明效果,反走样)等。
4、接下来我们具体考虑裁剪Clipping,显然有三种情形:接受/保留、拒绝/剔除、裁剪/分割。二维的相对于裁剪窗,三维的相对于裁剪体。很容易想到,裁剪对于线段和多边形很容易进行,但对于曲线和文本很难进行------将它们转化为线段和多边形即可。然后,最直观的计算办法就是计算线段与裁剪窗口边界的交点,但这很低效,因为每次求交点运算都需要一次除法。
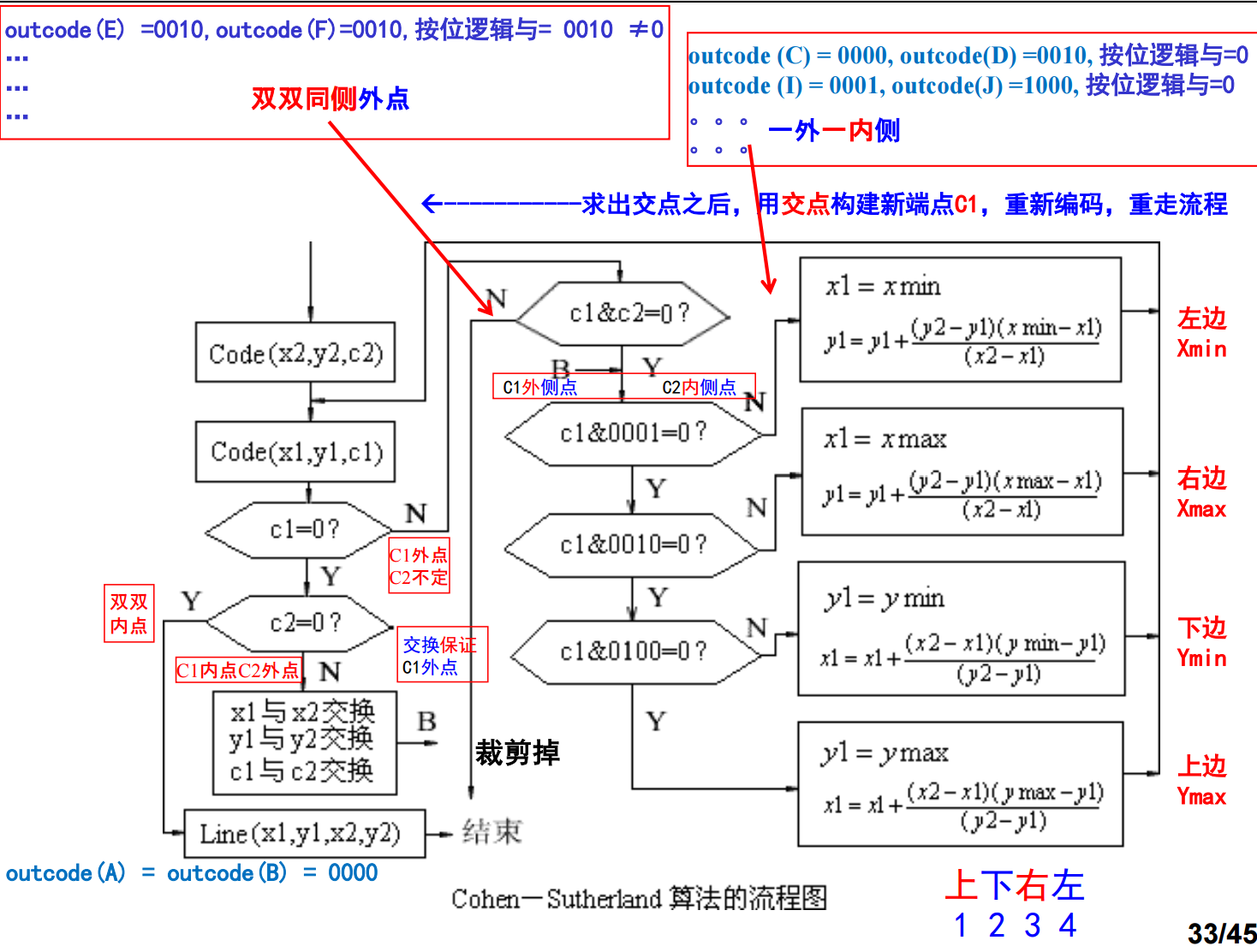
5、我们来考虑Cohen-Sutherland算法:
Case 1: 线段的两个端点都在裁剪窗口内,则原样绘制直线,即接受。
Case 2: 线段的两个端点都在窗口外,且在同一条直线的外侧,则丢弃这条直线,即拒绝。
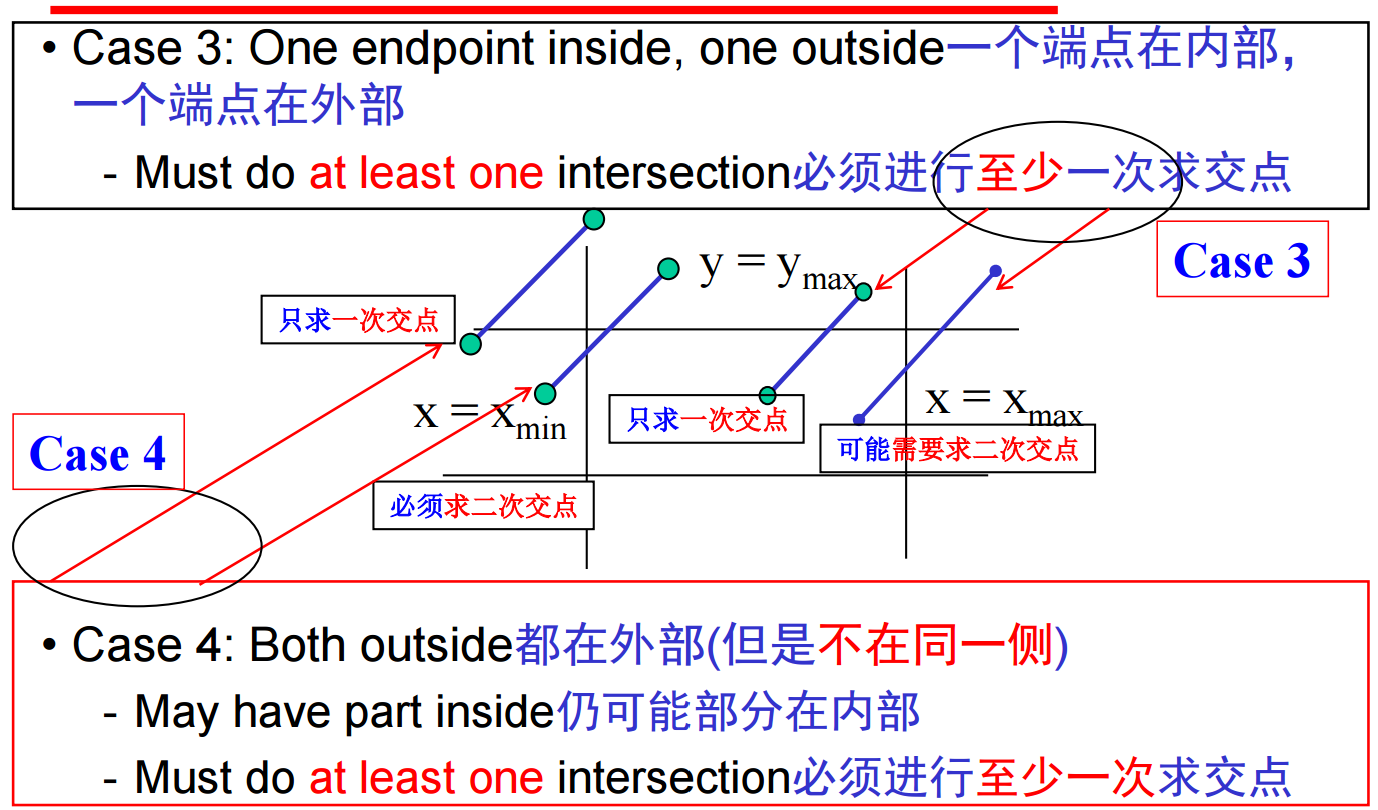

对于上述编码,我们可以看下图:
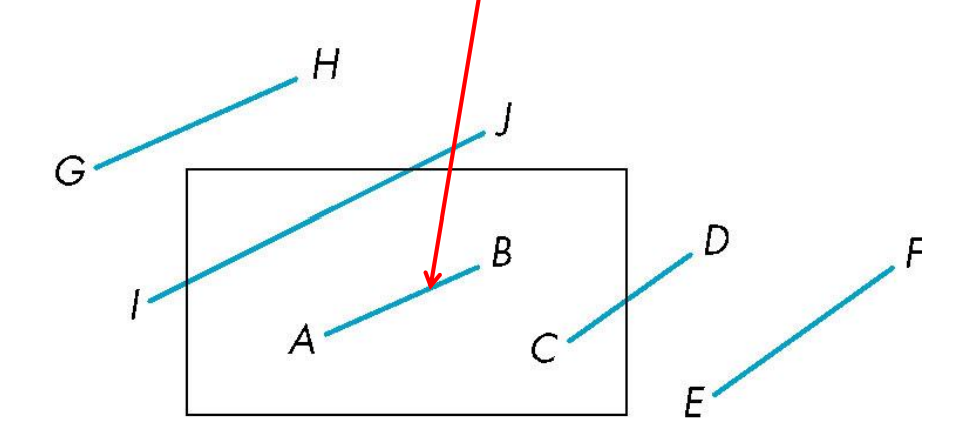
①AB:编码(A) = 编码(B) = 0000,为可接受线段。
②CD:编码(C) = 0000,编码(D) =0010≠0,在编码(D)中的1确定线段与哪条边相交(图中为右边)。如果有一条从点A出发的线段,另一端点的编码中有两个1,那么可能需要进行两次求交点(比如编码K=1010)。
③EF:编码(E) 与 编码(F) 的按位逻辑与= 0010 ≠0,即两个编码中有某一位同时等于1,线段在裁剪窗口的对应同一边界的外侧,拒绝。
④GH和IJ的端点在窗口外,具有相似的编码,不全是零,但逻辑与为0。这个时候可以通过与窗口一条边求交点缩短线段(如何缩短?上下右左),然后计算新端点的编码,重新执行前述算法。
6、在绝大多数应用中,裁剪窗口相对于整个对象数据库而言是比较小的。大多数线段是在窗口的一条边或多条边外面,从而可以基于编码把它们丢弃。当线段需要用多步进行缩短时,代码要被重复执行,这时效率不高。求交点时采用直线的斜截式(显示形式)表示:y=mx+h。我们来看Cohen-Sutherland算法的流程: