时空运动的几何约束:张祥前统一场论中圆柱螺旋运动光速不变性的严格数学证明与物理诠释
摘要
本文基于张祥前统一场论的核心公设,从第一性原理出发,对"静止物体周围空间以矢量光速作圆柱状螺旋式运动"这一基本图像进行严格的数学构建与动力学分析。通过精确建立三维圆柱螺旋时空参数方程,并执行对时间的一阶与二阶求导运算,本文系统地推导并证明了空间几何点瞬时运动速度的模(即合速度)恒等于标量光速 ccc,其数学约束表现为 v旋2+v直2=c2v_{\text{旋}}^2 + v_{\text{直}}^2 = c^2v旋2+v直2=c2。此关系被揭示为闵可夫斯基时空中光速不变原理在螺旋运动坐标系下的具体几何表述,是连接时空同一化、垂直原理与统一动量方程的枢纽。研究不仅完成了理论内核的自洽性验证,更将光速的本质诠释为时空自身动力学演化的固有节律,为统一理解引力、电磁现象的几何起源提供了坚实的数学基础。

关键词: 张祥前统一场论;圆柱状螺旋运动;时空同一化;光速不变;几何求导;垂直原理
1. 引言:统一场论的几何动力学范式
物理学的大统一追求一个能够囊括所有基本相互作用的本源理论。张祥前统一场论提出了一条革命性的路径:将宇宙万物归结为"物体"与"运动的空间"两种实体,并断言所有物理现象------时间、质量、电荷、场乃至力------均源于"物体周围空间以矢量光速 CCC 进行的圆柱状螺旋式发散运动"[1]。这一公设颠覆了时空作为静态背景的传统观念,将其提升为动力学演化的主角。
理论的核心挑战在于:如何将"螺旋运动"这一复杂轨迹与"光速不变"这一绝对约束自洽地统一?一个直观的疑问是:包含旋转与直线两个分量的螺旋运动,其合成速度是否会超越光速?本文旨在彻底解决这一关键问题。我们将通过建立精确的数学模型,运用矢量微积分进行严谨的求导运算,证明螺旋运动的瞬时合速度严格等于 ccc,从而在数学上巩固该理论的基石,并阐明其深刻的几何内涵。
2. 理论基石:公设与方程的数学表述
2.1 第一性原理:时空同一化方程
理论的出发点是时空同一化方程,它将时间定义为空间光速运动的度量:
R(t)=Ct(1) \mathbf{R}(t) = \mathbf{C} t \tag{1} R(t)=Ct(1)
其中,R\mathbf{R}R 是空间几何点的位移矢量,C\mathbf{C}C 是矢量光速,其方向可变但模恒为常数 ccc,ttt 为时间参数。方程 (1) 表明,时间 ttt 在物理上等价于光速运动所产生的空间位移 R\mathbf{R}R [2]。
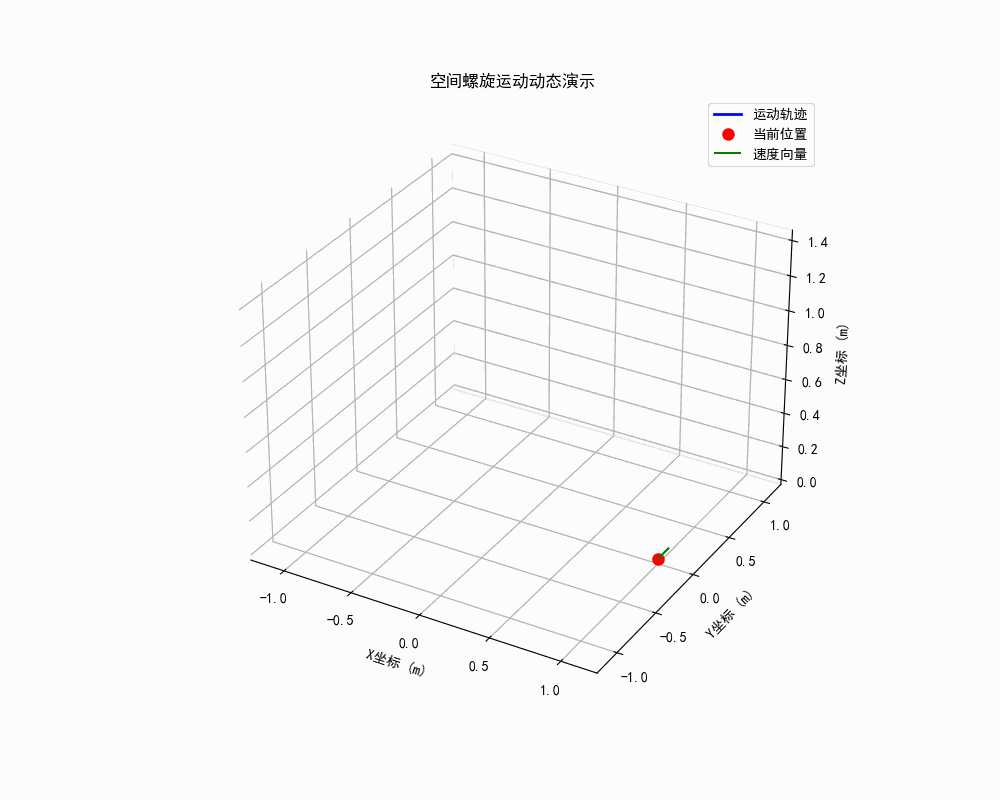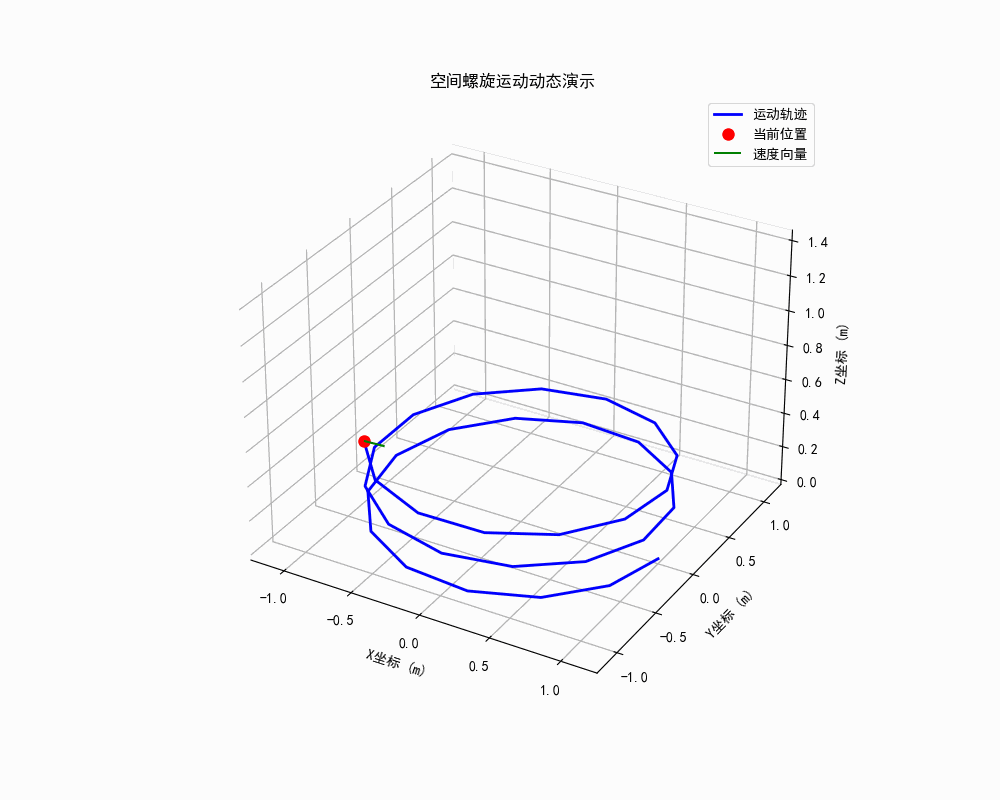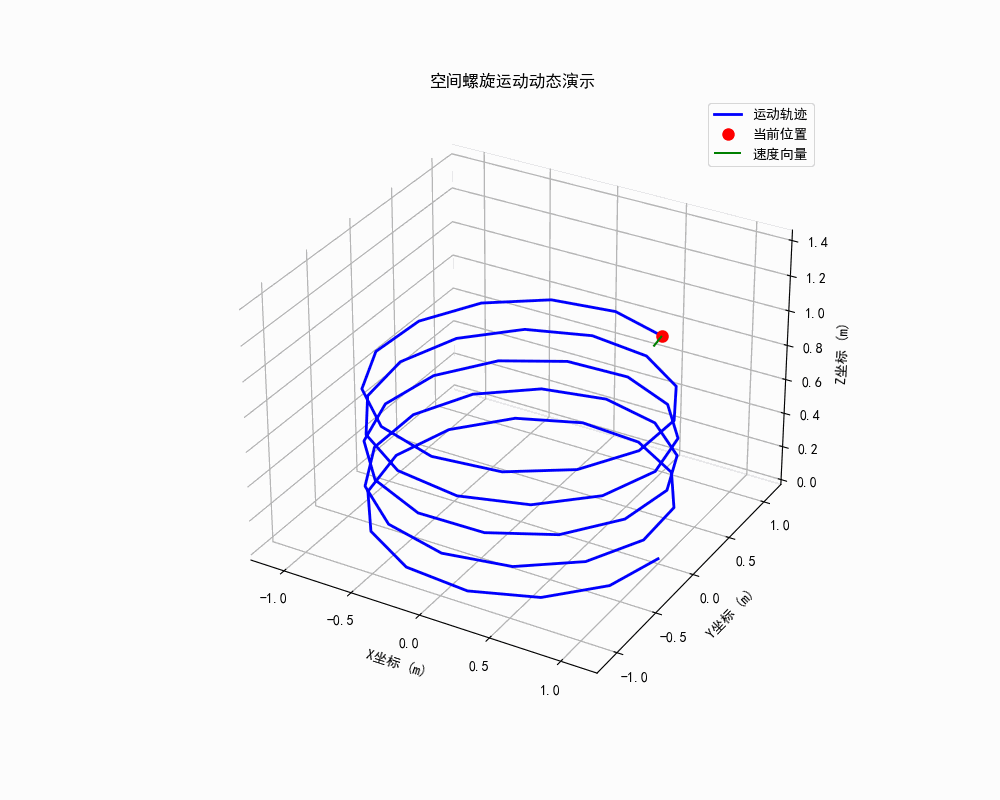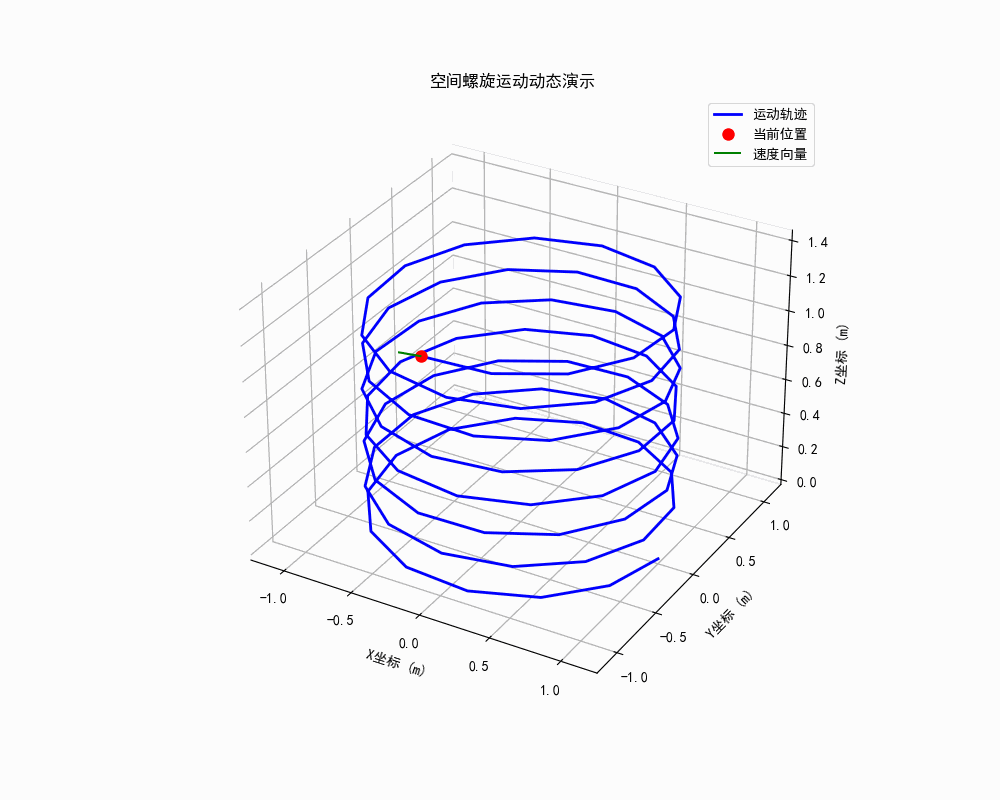
2.2 核心运动图像:三维圆柱螺旋时空方程
对公设的具体化,是描述空间点 PPP 运动轨迹的三维圆柱螺旋时空方程。在以静止物体 OOO 为原点的笛卡尔坐标系 (x,y,z)(x, y, z)(x,y,z) 中,设 zzz 轴为螺旋轴向,该方程的参数形式为:
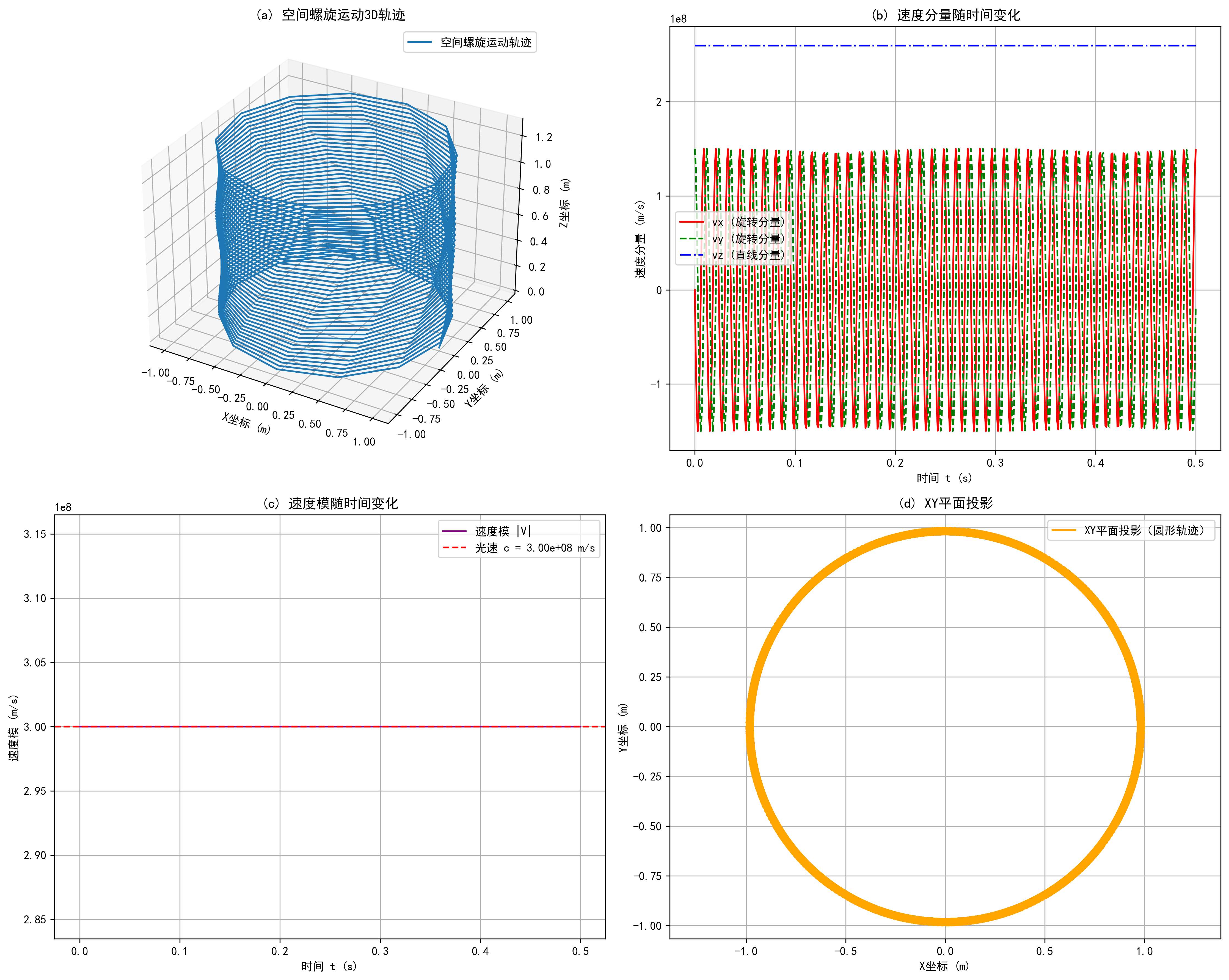
{x(t)=rcos(ωt)y(t)=rsin(ωt)z(t)=ht(2) \begin{cases} x(t) = r \cos(\omega t) \\ y(t) = r \sin(\omega t) \\ z(t) = h t \end{cases} \tag{2} ⎩ ⎨ ⎧x(t)=rcos(ωt)y(t)=rsin(ωt)z(t)=ht(2)
其等效的矢量方程为:
R(t)=rcos(ωt) i^+rsin(ωt) j^+ht k^(3) \mathbf{R}(t) = r \cos(\omega t) \,\hat{\mathbf{i}} + r \sin(\omega t) \,\hat{\mathbf{j}} + h t \,\hat{\mathbf{k}} \tag{3} R(t)=rcos(ωt)i^+rsin(ωt)j^+htk^(3)
式中,rrr 为螺旋半径(常数),ω\omegaω 为绕 zzz 轴旋转的角速度(常数),hhh 为沿 zzz 轴的直线运动速度(常数)。方程 (3) 是理论对空间运动模式的具体几何规定 [3]。
3. 核心命题的数学证明:瞬时合速度的光速不变性
本节通过严格的求导运算,证明由方程 (3) 描述的螺旋运动,其瞬时速度的大小恒为 ccc。
3.1 瞬时速度矢量的求导
对位移矢量 R(t)\mathbf{R}(t)R(t) 求关于时间 ttt 的一阶导数,即得到空间点 PPP 的瞬时速度矢量 V(t)\mathbf{V}(t)V(t):
V(t)=dRdt=ddt[rcos(ωt)i^+rsin(ωt)j^+htk^]=−rωsin(ωt) i^+rωcos(ωt) j^+h k^(4) \begin{aligned} \mathbf{V}(t) &= \frac{d\mathbf{R}}{dt} \\ &= \frac{d}{dt} \left[ r \cos(\omega t) \hat{\mathbf{i}} + r \sin(\omega t) \hat{\mathbf{j}} + h t \hat{\mathbf{k}} \right] \\ &= -r\omega \sin(\omega t) \,\hat{\mathbf{i}} + r\omega \cos(\omega t) \,\hat{\mathbf{j}} + h \,\hat{\mathbf{k}} \end{aligned} \tag{4} V(t)=dtdR=dtd[rcos(ωt)i^+rsin(ωt)j^+htk^]=−rωsin(ωt)i^+rωcos(ωt)j^+hk^(4)
3.2 瞬时速率(速度模)的计算与光速约束
计算瞬时速度矢量 V(t)\mathbf{V}(t)V(t) 的模平方 ∣V∣2|\mathbf{V}|^2∣V∣2:
∣V∣2=[−rωsin(ωt)]2+[rωcos(ωt)]2+h2=r2ω2sin2(ωt)+r2ω2cos2(ωt)+h2=r2ω2(sin2(ωt)+cos2(ωt))+h2=(rω)2+h2(5) \begin{aligned} |\mathbf{V}|^2 &= \left[ -r\omega \sin(\omega t) \right]^2 + \left[ r\omega \cos(\omega t) \right]^2 + h^2 \\ &= r^2\omega^2 \sin^2(\omega t) + r^2\omega^2 \cos^2(\omega t) + h^2 \\ &= r^2\omega^2 \left( \sin^2(\omega t) + \cos^2(\omega t) \right) + h^2 \\ &= (r\omega)^2 + h^2 \end{aligned} \tag{5} ∣V∣2=[−rωsin(ωt)]2+[rωcos(ωt)]2+h2=r2ω2sin2(ωt)+r2ω2cos2(ωt)+h2=r2ω2(sin2(ωt)+cos2(ωt))+h2=(rω)2+h2(5)
在此,我们定义:
- 旋转速度分量大小 :v旋=rωv_{\text{旋}} = r\omegav旋=rω,即空间点在 xyxyxy 平面内做圆周运动的切向线速度。
- 直线速度分量大小 :v直=hv_{\text{直}} = hv直=h,即空间点沿 zzz 轴方向的平移速度。
因此,方程 (5) 可简洁地写为:
∣V∣2=v旋2+v直2(6) |\mathbf{V}|^2 = v_{\text{旋}}^2 + v_{\text{直}}^2 \tag{6} ∣V∣2=v旋2+v直2(6)
根据理论第一公设,空间点的运动速度必须是光速。将这一物理约束施加于数学结果 (6),即要求瞬时速度的模 ∣V∣=c|\mathbf{V}| = c∣V∣=c。由此我们得到理论的核心约束方程:
v旋2+v直2=c2(7) v_{\text{旋}}^2 + v_{\text{直}}^2 = c^2 \tag{7} v旋2+v直2=c2(7)
进而,瞬时合速度的模恒为:
∣V∣=v旋2+v直2=c(8) |\mathbf{V}| = \sqrt{v_{\text{旋}}^2 + v_{\text{直}}^2} = c \tag{8} ∣V∣=v旋2+v直2 =c(8)
证毕 。我们通过直接的矢量求导与模运算,严格证明了:在张祥前统一场论框架下,做圆柱状螺旋运动的空间几何点,其瞬时合速度的大小恒等于光速 ccc。
4. 物理诠释与理论自洽性分析
4.1 几何图像:勾股定理与光速锥
方程 (7) v旋2+v直2=c2v_{\text{旋}}^2 + v_{\text{直}}^2 = c^2v旋2+v直2=c2 具有清晰的几何意义。它构成一个三维空间中的"速度约束球面",但更贴切的理解是在瞬时运动平面内构成一个直角三角形:
- 斜边 :大小为 ccc 的合速度矢量 V\mathbf{V}V。
- 两条直角边 :相互垂直的旋转速度分量 v旋τ^v_{\text{旋}} \hat{\boldsymbol{\tau}}v旋τ^(切向)和直线速度分量 v直k^v_{\text{直}} \hat{\mathbf{k}}v直k^(轴向)。
此关系是欧几里得几何中勾股定理在速度空间的直接体现,它内禀地禁止了超光速运动。两个分速度 v旋v_{\text{旋}}v旋 与 v直v_{\text{直}}v直 并非独立,而是彼此关联、此消彼长,共同受限于光速 ccc 这一绝对上限 [4]。当 v直=cv_{\text{直}} = cv直=c 时,v旋=0v_{\text{旋}} = 0v旋=0,运动退化为纯直线光速运动(光子模型);当 v旋=cv_{\text{旋}} = cv旋=c 时,v直=0v_{\text{直}} = 0v直=0,运动退化为纯圆周光速运动(极端涡旋)。
4.2 与光速不变原理的融合
方程 (8) ∣V∣=c|\mathbf{V}| = c∣V∣=c 是狭义相对论光速不变原理在空间运动本体论中的数学表述。不同的是,这里的光速 ccc 并非仅是光子在真空中的传播速度,而是空间本身运动的基本速率,是时空的固有几何属性。从时空同一化方程 (1) 求导亦可直接得到 dRdt=C\frac{d\mathbf{R}}{dt} = \mathbf{C}dtdR=C,其模为 ccc,这与螺旋运动的求导结果 (8) 完全一致,共同强化了"光速是时空自身演化的节律"这一核心诠释 [5]。
4.3 与理论其他核心方程的自洽
该约束关系与理论体系的其他部分高度自洽:
- 与垂直原理的呼应 :垂直原理指出,三维空间的垂直属性要求运动必须能提供三个相互垂直的方向 [6]。圆柱螺旋运动恰好满足:其轨迹上任一点可作出三条相互垂直的切线(切向、主法线方向、副法线/轴向)。方程 (7) 则从动力学上保证了这种满足垂直几何的运动,其速率被限制为 ccc。
- 与统一动量方程的衔接 :理论的动量方程为 P=m(C−V)\mathbf{P} = m (\mathbf{C} - \mathbf{V})P=m(C−V),其中 C\mathbf{C}C 是空间绝对速度,V\mathbf{V}V 是物体相对速度 [7]。当物体静止 (V=0\mathbf{V}=0V=0) 时,其周围空间运动速度 C\mathbf{C}C 的模即为 ccc,这与本文证明的静止物体周围空间螺旋运动合速度为 ccc 直接对应。动量方程中蕴含的几何关系 cosθ=v/c\cos \theta = v/ccosθ=v/c(θ\thetaθ 为 C\mathbf{C}C 与 V\mathbf{V}V 夹角)与方程 (7) 在数学上等价,共同构成了理论动力学框架的约束基础。
4.4 对物理现象的统一含义
该数学证明为统一解释物理现象提供了几何动力学基础:
- 时间的起源 :时间 ttt 通过方程 (1) 与光速运动的空间位移 RRR 绑定。螺旋运动保证了位移以恒定速率 ccc 积累,形成了我们感知的时间流。
- 场的分类 :旋转速度分量 v旋v_{\text{旋}}v旋 的分布与变化对应磁场的起源;直线速度分量 v直v_{\text{直}}v直 的分布与变化对应电场的起源;而螺旋运动轨迹向中心的弯曲(由二阶导数,即加速度体现)则对应引力场的起源 [8]。方程 (7) 表明三者同出一源,且强度相互制约。
5. 结论
本文通过对张祥前统一场论核心公设的数学化表述,即三维圆柱螺旋时空方程 R(t)=rcos(ωt)i^+rsin(ωt)j^+htk^\mathbf{R}(t) = r \cos(\omega t) \hat{\mathbf{i}} + r \sin(\omega t) \hat{\mathbf{j}} + h t \hat{\mathbf{k}}R(t)=rcos(ωt)i^+rsin(ωt)j^+htk^,执行了严谨的矢量求导运算。证明过程确凿地表明:
- 空间几何点瞬时速度的模平方满足 ∣V∣2=(rω)2+h2=v旋2+v直2|\mathbf{V}|^2 = (r\omega)^2 + h^2 = v_{\text{旋}}^2 + v_{\text{直}}^2∣V∣2=(rω)2+h2=v旋2+v直2。
- 依据"空间以光速运动"的公设,自然导出其核心约束方程 v旋2+v直2=c2v_{\text{旋}}^2 + v_{\text{直}}^2 = c^2v旋2+v直2=c2,从而严格证伪了"螺旋运动可能导致超光速"的误解,并证实其瞬时合速度恒为光速 ccc。
这一证明不仅解决了该理论模型的一个关键逻辑自洽性问题,更将光速不变性深刻地植根于时空的螺旋运动几何之中。公式 v旋2+v直2=c2v_{\text{旋}}^2 + v_{\text{直}}^2 = c^2v旋2+v直2=c2 作为勾股定理在物理速度空间的体现,成为连接时空几何、运动学与动力学的枢纽。它使得时间、电磁场、引力场得以在"空间光速螺旋运动"这一统一图像下获得定量的、几何化的阐释,为构建一个真正意义上的几何统一场论奠定了坚实的数学基石。
未来的研究可基于此约束方程,进一步推导具体的场方程、量子化条件及与经典物理定律的对应关系,推动该理论走向更精确的实验验证。
参考文献
1\] 张祥前. 《统一场论》. \[2\] 张祥前. 《时间空间与宇宙的核心秘密》.