数据结构算法——排序算法解析

1、快排

快速排序：

将子序列划分为两个部分S1、S2，并且满足S1中最大值小于S2中最小值。
这样，在子序列分别递归的排序之后，原序列自然有序。
轴点：左 / 右侧的元素，均不比它更大 / 小。
轴点自然的将序列分为了符合之前条件的两个部分，剩下的部分只需递归完成即可。

template <typename T>
void Vector<T>::quickSort ( Rank lo, Rank hi ) {
if ( hi - lo < 2 ) return; //单元素区间自然有序，否则...
Rank mi = partition ( lo, hi ); //在[lo, hi)内构造轴点
quickSort ( lo, mi ); //对前缀递归排序
quickSort ( mi + 1, hi ); //对后缀递归排序
}
但是，轴点在原始序列中未必存在。轴点存在的必要条件是，轴点在序列中所在的位置必定是其排序后所在的位置（就位）。
在有序序列中，所有元素都是轴点。因此快排就是将所有元素逐个转换为轴点的过程。通过适当的交换，可使任一元素转换为轴点。
轴点的构造：
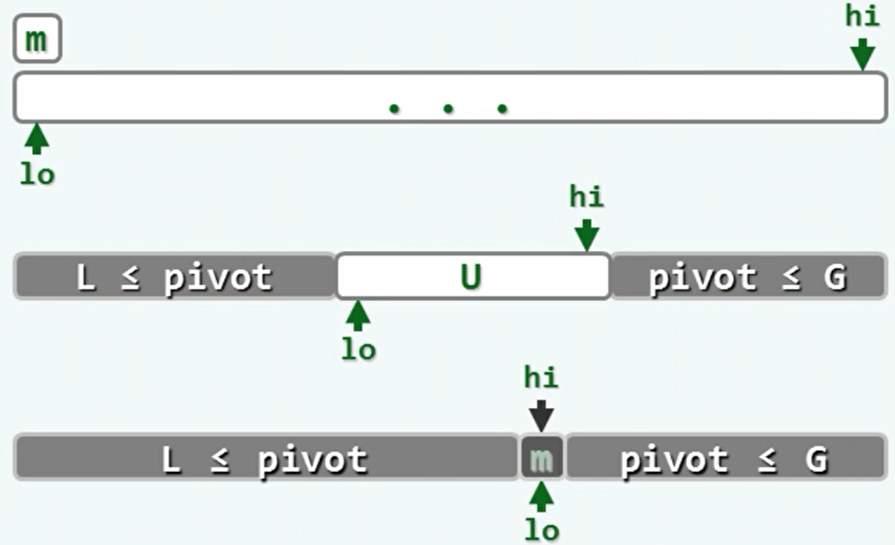
- 以首元素m为轴点为例，使用lo和hi两个指针，将序列分为三部分。L是从前往后的小于等于m的部分，G是从后往前的大于等于m的部分，U是未扫描的部分。lo和hi指向U的边界。
- lo和hi向中间扫描，最终重合的位置就是m作为轴点所在的位置。

具体的，在算法进行的开始，先去除m并备份。这样原来m的位置就空闲了，并由lo指向。
然后hi开始扫描，遇到大于等于m的就越过，遇到小于m的就将其移至lo指向的空闲位置。然后改为lo扫描，hi空闲。
最后扫描完成后，将备份的m移入空闲位置。

时间复杂度最好O(nlog n)，最坏O(n^2)，平均O(nlog n)。

快速排序的变种：

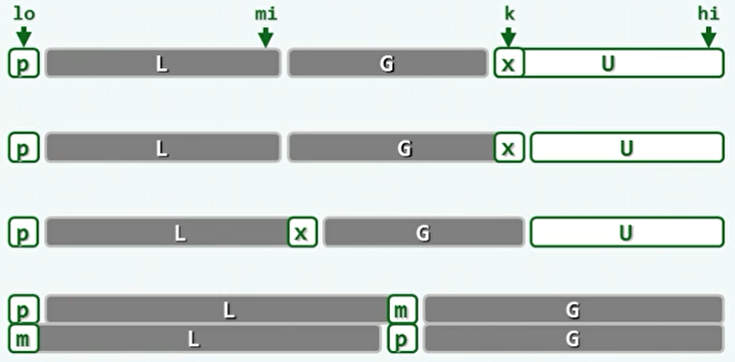
同样的将整个序列分为四部分，只不过待处理部分U在最后端，而P也不需要取出备份。
k指针从头后移，遇到大于等于轴点的元素就只后移，相当于将该元素归入G。遇到小于轴点的元素，则与G中的首元素交换位置，相当于将该元素归入L，然后再后移。
最后U的规模为0时，将位于序列首端的轴点P与L中的最后一个元素交换位置。

复制代码

template <typename T> //轴点构造算法：通过调整元素位置构造区间[lo, hi)的轴点，并返回其秩
Rank Vector<T>::partition ( Rank lo, Rank hi ) { //版本C
   swap ( _elem[lo], _elem[ lo + rand() % ( hi - lo ) ] ); //任选一个元素与首元素交换
   T pivot = _elem[lo]; //以首元素为候选轴点------经以上交换，等效于随机选取
   int mi = lo;
   for ( int k = lo + 1; k < hi; k++ ) //自左向右扫描
      if ( _elem[k] < pivot ) //若当前元素_elem[k]小于pivot，则
         swap ( _elem[++mi], _elem[k] ); //将_elem[k]交换至原mi之后，使L子序列向右扩展
   swap ( _elem[lo], _elem[mi] ); //候选轴点归位
   return mi; //返回轴点的秩
}

2、选取

众数：这里指的是出现次数超过序列长度一半以上的元素。
这种定义下，如果存在众数，则其必然也是中位数。
减而治之：
- 若在向量A的前缀P（P长度为偶数）中，元素x出现的次数恰占半数，则A有众数仅当，对应的后缀A --Р有众数m，且m就是A的众数。
- 若x= m，则在排除前缀P之后，m与其它元素在数量上的差距保持不变。
- 若x ≠ m，则在排除前缀Р之后，m与其它元素在数量上的差距不致缩小。

用一个计数器记录众数的候选者与其他元素的数量差。

template <typename T> T majEleCandidate ( Vector<T> A ) { //选出具备必要条件的众数候选者
T maj; //众数候选者
// 线性扫描：借助计数器c，记录maj与其它元素的数量差额
for ( int c = 0, i = 0; i < A.size(); i++ )
if ( 0 == c ) { //每当c归零，都意味着此时的前缀P可以剪除
maj = A[i]; c = 1; //众数候选者改为新的当前元素
} else //否则
maj == A[i] ? c++ : c--; //相应地更新差额计数器
return maj; //至此，原向量的众数若存在，则只能是maj ------ 尽管反之不然
}
选取的通用算法：
选取的目标是，取出序列中经排序后秩为k的元素。
quickSelect()：
- 借鉴快排的思想，如果轴点的秩恰好为k，则直接返回。
- 如果轴点的秩不是k，但可通过与轴点的秩比较，得出k是在L中还是在G中。

点击链接数据结构算法------排序算法解析阅读原文