【浮点运算性能优化】浮点转定点算法库的多平台通用移植方案与性能评估优化

一、背景

---

出于项目需求，要在一块超低成本的芯片CIU32F003上运行大量浮点数乘除法，同时又需要保证芯片的运行频率达标，为此，必须对浮点数算法进行优化。

二、在什么情况下你会需要浮点转定点算法

---

1、在没有浮点运算单元硬件(FPU等)支持的平台上运行大量浮点计算，只能通过软件来实现性能优化；

2、需要进行大量的浮点数运算以至于拖累了设备的运行效率；

三、本文提供的算法具备的优势

---

1、提供fr_math和TI的IQmath两种算法库以及其移植方案；

2、高效的浮点转定点算法，从而优化浮点数的加减乘除以及其他更复杂的正弦余弦等数学运算；

3、以C语言源代码的方式提供库，没有平台依赖，可在多平台移植，只需要包含头文件并编译即可（我轻松实现了将库移植到没有什么名气的低成本嵌入式平台上，所有若是你需要将其移植到Win/Linux或其他平台应该是更加轻松的）；

4、IQmath算法库有针对TI平台的专门硬件优化，若您已使用TI平台的芯片，建议您根据DSP版本查找和使用相应的IQmath，相较于纯软件的实现它会拥有更高的性能；

5、网络上有文章反馈，部分STM32平台芯片自带的硬件加速支持的float算法速度可能会没有IQmath的纯软件支持效率高。

四、浮点转定点算法原理简介

---

1、数据存储原理

数据以二进制方式在计算机上存储，以int和float为例子，两者通常在32位编译器中都是占4个字节，即32位的。

其中

int的结构为：1位符号位+31位数值位；

float结构为：1位符号位+8位指数位+23位尾数位；

2、数据转换原理

由上述数据结构，我们可以得出将浮点数转换为定点数的公式：

定点数 = 浮点数 × 2^n(n为小数宽)

由于二进制的特性，数据*2可表示为将数据左移1位，移位运算在计算机中需要的算力是较低的，因此，我们需要保留多少位宽作为小数就将float类型数据左移多少位，即可得到转换后的定点数。

例如：浮点数0.002，可以通过左移3位将其表示为定点数2，运算完成后再将结果右移回去，即可转换回浮点数；

同样的，根据我们选择的小数位位宽的大小，小数位宽越大，数据精度越高，但是数据的整体范围会越小，具体的表现可参考IQmath库提供的精度表格：

Type	Integer Bits	Fractional Bits	Min Range	Max Range	Resolution
_iq30	2	30	-2	1.999 999 999	0.000 000 001
_iq29	3	29	-4	3.999 999 998	0.000 000 002
_iq28	4	28	-8	7.999 999 996	0.000 000 004
_iq27	5	27	-16	15.999 999 993	0.000 000 007
_iq26	6	26	-32	31.999 999 985	0.000 000 015
_iq25	7	25	-64	63.999 999 970	0.000 000 030
_iq24	8	24	-128	127.999 999 940	0.000 000 060
_iq23	9	23	-256	255.999 999 881	0.000 000 119
_iq22	10	22	-512	511.999 999 762	0.000 000 238
_iq21	11	21	-1,024	1,023.999 999 523	0.000 000 477
_iq20	12	20	-2,048	2,047.999 999 046	0.000 000 954
_iq19	13	19	-4,096	4,095.999 998 093	0.000 001 907
_iq18	14	18	-8,192	8,191.999 996 185	0.000 003 815
_iq17	15	17	-16,384	16,383.999 992 371	0.000 007 629
_iq16	16	16	-32,768	32,767.999 984 741	0.000 015 259
_iq15	17	15	-65,536	65,535.999 969 483	0.000 030 518
_iq14	18	14	-131,072	131,071.999 938 965	0.000 061 035
_iq13	19	13	-262,144	262,143.999 877 930	0.000 122 070
_iq12	20	12	-524,288	524,287.999 755 859	0.000 244 141
_iq11	21	11	-1,048,576	1,048,575.999 511 720	0.000 488 281
_iq10	22	10	-2,097,152	2,097,151.999 023 440	0.000 976 563
_iq9	23	9	-4,194,304	4,194,303.998 046 880	0.001 953 125
_iq8	24	8	-8,388,608	8,388,607.996 093 750	0.003 906 250
_iq7	25	7	-16,777,216	16,777,215.992 187 500	0.007 812 500
_iq6	26	6	-33,554,432	33,554,431.984 375 000	0.015 625 000
_iq5	27	5	-67,108,864	67,108,863.968 750 000	0.031 250 000
_iq4	28	4	-134,217,728	134,217,727.937 500 000	0.062 500 000
_iq3	29	3	-268,435,456	268,435,455.875 000 000	0.125 000 000
_iq2	30	2	-536,870,912	536,870,911.750 000 000	0.250 000 000
_iq1	31	1	-1,073,741,824	1,073,741,823.500 000 000	0.500 000 000

3、数据乘除法原理

简单理解上述的数据转换原理：

我们将浮点数乘以一个倍数（2^n），从而将小数位的数据放大到了整数位上表示(由此，放大的倍数不够会导致精度的丢失)。

因此我们将两个浮点数转换为定点数后进行乘法，放大的倍数（2^n）也会随之进行乘法运算，我们需要将其进行缩放，以回到原始设定的精度。

3.1乘法案例

假设我们用 Q22 格式（即小数部分占 22 位）：
X f i x e d = X f l o a t × 2 22 X_{fixed} = X_{float} \times 2^{22} Xfixed=Xfloat×222

两个Q22的定点数相乘：
Z = X × Y Z = X \times Y Z=X×Y

实际运算：整数乘法→得到64位结果(32位 × 32位 = 64位 )

结果缩放：两个数都被乘了 2 22 2^{22} 222，再进行乘法，结果相当于乘了 2 44 2^{44} 244，需要将结果缩放回Q22格式，即右移22位：
Z f i x e d = X f i x e d × Y f i x e d 2 22 Z_{fixed} = \frac{X_{fixed} \times Y_{fixed}} {2^{22}} Zfixed=222Xfixed×Yfixed

总结：定点乘法=整数乘法+结果缩放(右移)

3.2除法案例

假设我们用 Q22 格式（即小数部分占 22 位）：

两个Q22的定点数相除：
Z = X Y Z = \frac{X}{Y} Z=YX

结果缩放：两个数都被乘了 2 22 2^{22} 222，再进行除法，会丢失缩放信息，需要将结果缩放回Q22格式，即左移22位：
Z f i x e d = X f i x e d × 2 22 Y f i x e d Z_{fixed} = \frac{X_{fixed} \times {2^{22}}}{Y_{fixed}} Zfixed=YfixedXfixed×222

总结：定点除法=整数除法+预先左移(放大)

五、fr_math与IQmath算法库源码

---

为方便存档，我建立了一个github仓库(https://github.com/zaki-xie/fixedpoint-converter-lib/tree/main)

其中包含了两个库的源码（您在使用时任选其一即可，经过简单测试两者的运算精度是相同的，fr_math的封装更简单效率可能会更高，IQmath进行了更多校验可能会更安全但是效率会相对降低）

同时附上我获取到这两个库的原始开源地址：
fr_math(https://github.com/deftio/fr_math)
IQmath(https://github.com/mikisama/IQmath)

六、fr_math库的源码集成与性能测试

---

1、获取源码

获取fr_math\src文件夹下的所有代码文件

2、将源码添加到项目中

此处提供Keil下的项目配置方法，非常简单，在其他环境中配置是类似的。

将其放置到你项目的源码目录下，此处我放置到了如下路径：

源码目录\fr_math\

将以下库文件添加进项目即可

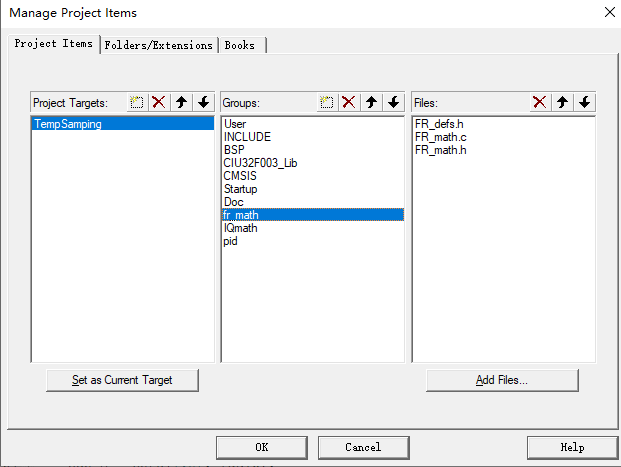
添加include path

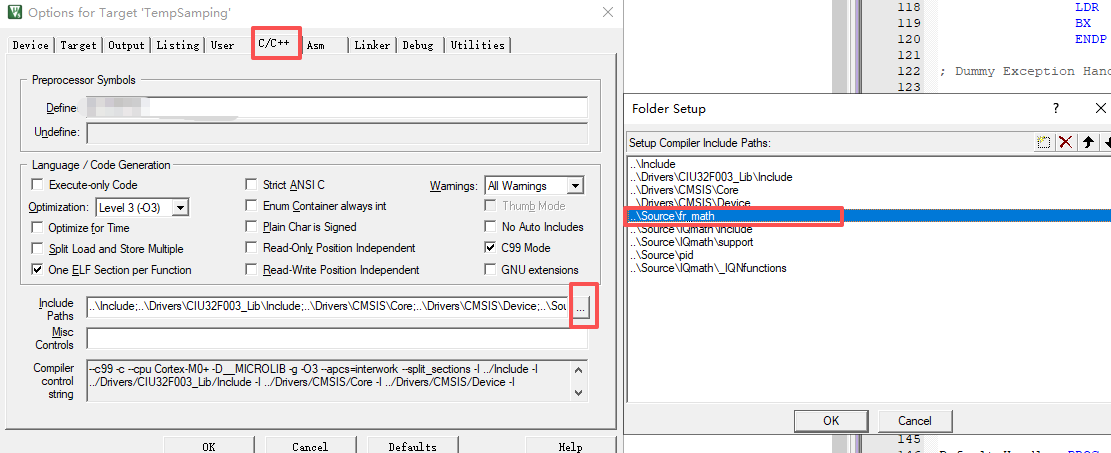
引用头文件

#include "FR_defs.h"
#include "FR_math.h"

如上操作，即可完成将fr_math的源码集成到项目中。

3、参考代码

调用FR内部封装的乘法函数进行1.2*1.11+3.5运算的测试案例，fr_math库的内部函数似乎都固定使用16位小数精度，若使用其他精度进行计算需要注意做额外的缩放以适配你的数据精度。

		/* FR_MATH库调用封装函数方案	*/
		s32 result_s32;
		float result_f;
		//计算A*B + C
		int radix = 22;  // 使用22位小数位
		s32 A = D2FR(1.2f, radix);
		s32 B = D2FR(1.11f, radix);
		s32 C = D2FR(3.5f, radix);
		
		//定点乘法，内部许多函数使用16位小数精度，需要注意
		s32 mul = FR_FixMuls(A, B);
		//由于库中函数默认用16位小数精度，在使用其他精度时需要进行额外的偏移
		result_s32 = mul >> (radix - 16);
		
		//支持不同精度操作的加法
		FR_ADD(result_s32, radix, C, radix);
		
		result_f = FR2D(result_s32, radix);

4、乘法性能测试

由于我是在嵌入式平台上运行，只能用比较麻烦的方式来评估性能；

我配置了一个输出引脚GPIO PB0，默认低电平，当运行fr_math库乘法时将引脚上拉，乘法运算完成后将引脚下拉，而后再添加一个延迟作为下降沿，防止主循环运行过快导致一直上拉，看不出上拉的时长；

使用如下的代码运行后，只需要用示波器测量PB0引脚的上升沿时间，即可评估乘法的效率；

诸位如果在其他更方便的平台运行，直接用定时器即可完成性能的测量。

		int radix = 22;
		s32 A = D2FR(1.2f, radix);
		s32 B = D2FR(1.11f, radix);
		s32 result_s32 = 0;
		s32 mul = 0;
		
		while(1)
		{
			std_gpio_set_pin(GPIOB,GPIO_PIN_0);//引脚上拉
			mul = FR_FixMuls(A, B);
			result_s32 = mul >> (radix - 16);
			std_gpio_reset_pin(GPIOB,GPIO_PIN_0);//引脚下拉
			std_delayus(5);//延迟
		} 

从下图可评估处，运行一次乘法运算(包含乘法和缩放的计算),需要约1.5us不到

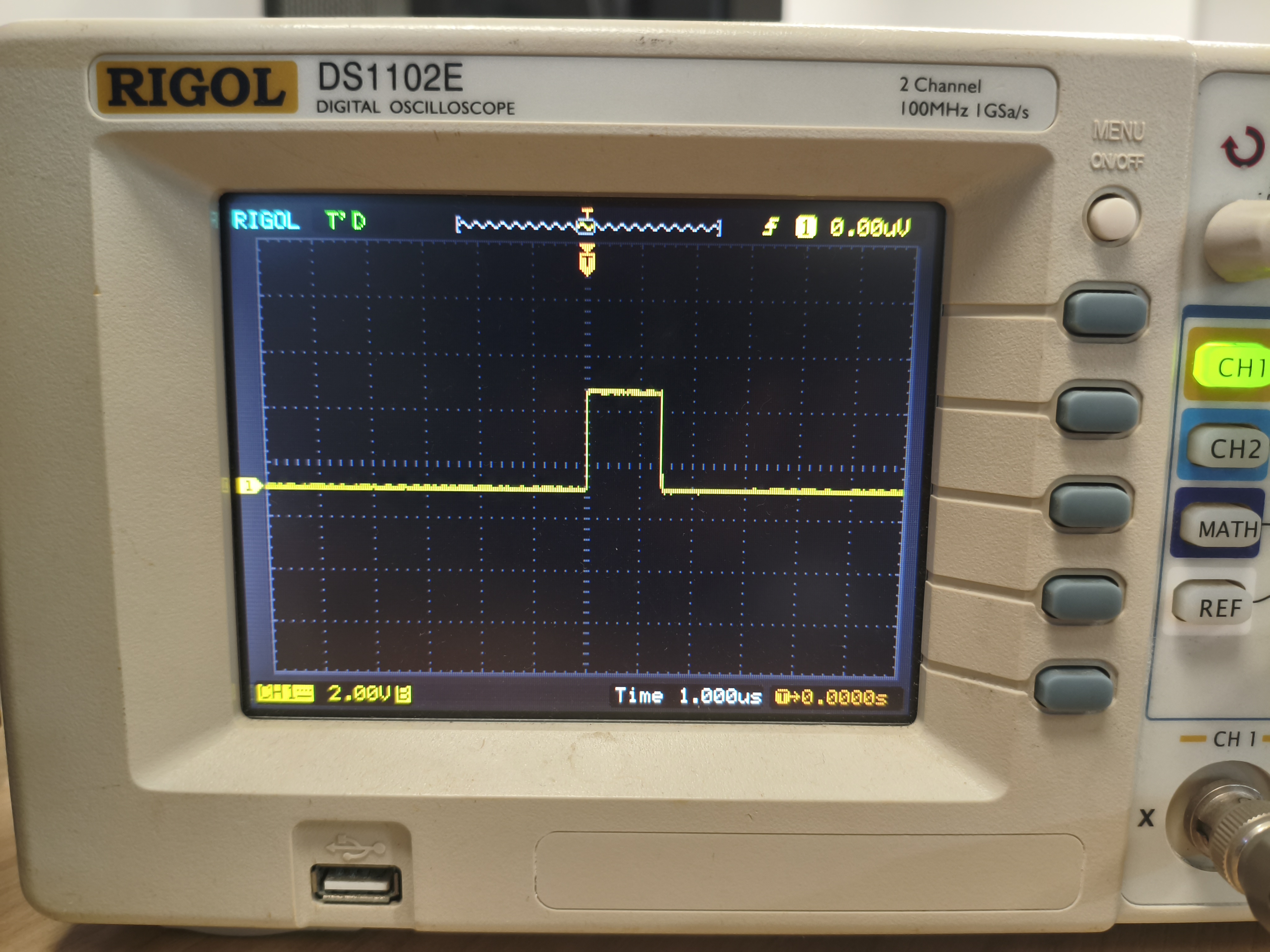
为了更严谨地评估，我们将测试范围拓展到运行100次乘法运算需要消耗多少时间

		int radix = 22;
		s32 A = D2FR(1.2f, radix);
		s32 B = D2FR(1.11f, radix);
		s32 result_s32 = 0;
		s32 mul = 0;
		uint32_t i;
		while(1)
		{
			std_gpio_set_pin(GPIOB,GPIO_PIN_0);//引脚上拉
			for(i = 0;i < 100; i++)
			{
				mul = FR_FixMuls(A, B);
				result_s32 = mul >> (radix - 16);
			}
			std_gpio_reset_pin(GPIOB,GPIO_PIN_0);//引脚下拉
			std_delayus(5);//延迟
		} 

运行100次乘法运算(包含乘法和缩放的计算),需要约150us

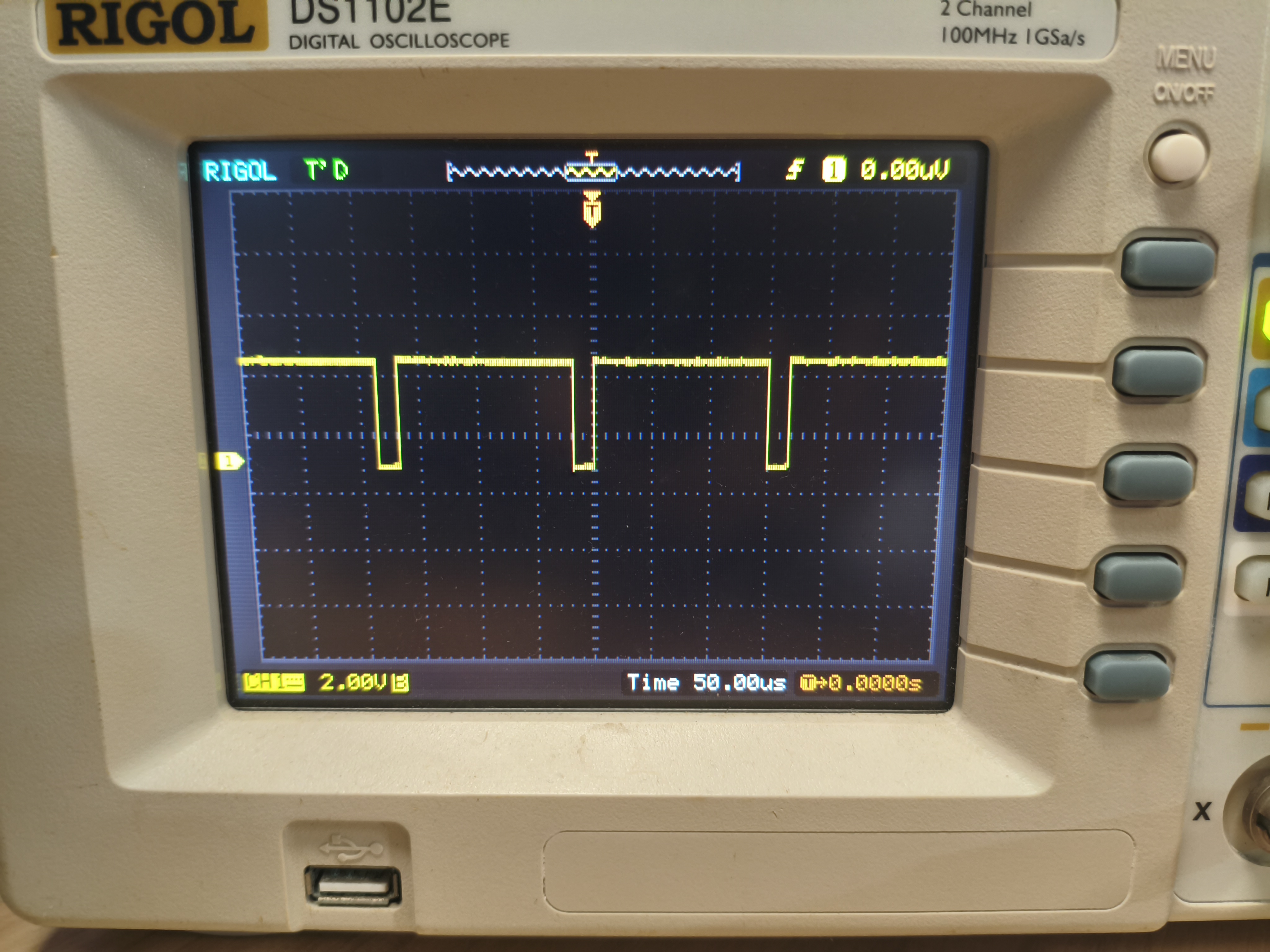
七、IQmath库的源码集成与性能测试

---

1、获取源码

相较于fr_math，IQmath的文件多了很多

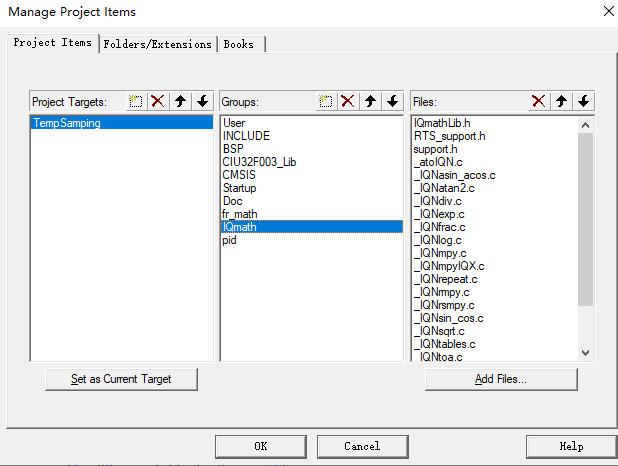
下图三个文件夹中代码都需要获取

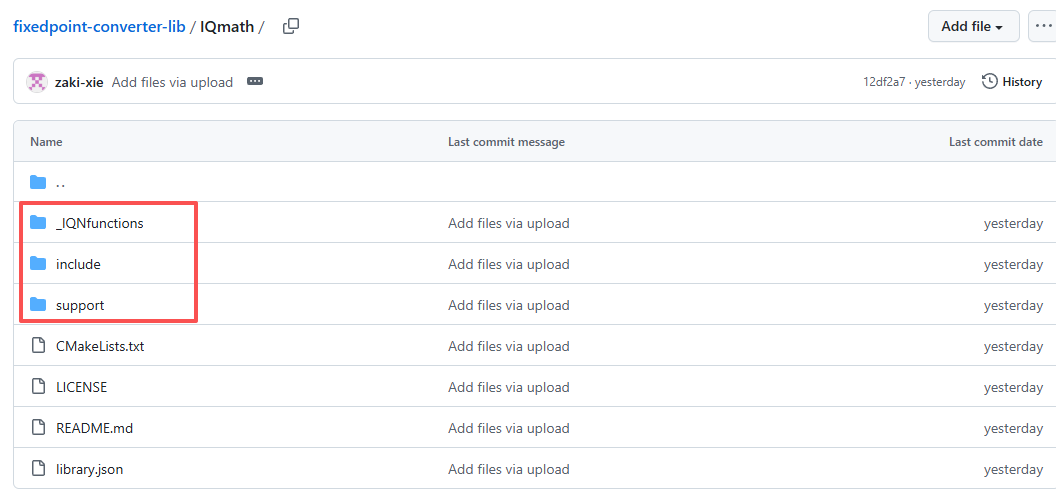
2、将源码添加到项目中

此处提供Keil下的项目配置方法，非常简单，在其他环境中配置是类似的。

将其放置到你项目的源码目录下，此处我放置到了如下路径：

源码目录\IQmath

和fr_math库添加时一样的捕捉，将所有IQmath源码添加到项目中

添加include路径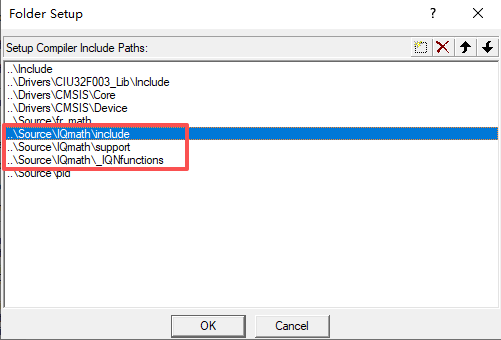

引用头文件

#include "IQmathLib.h"

3、参考代码

计算1.2*1.11+3.5

		_iq22 result_s32;
		float result_f;
		/*IQmath调用封装函数方案 */
		//计算A*B + C
		_iq22 A = _IQ22(1.2f);
		_iq22 B = _IQ22(1.11f);
		_iq22 C = _IQ22(3.5f);
		
		_iq22 mul = _IQ22mpy(A, B);
		result_s32 = mul + C;
		
		result_f = _IQ22toF(result_s32);

4、乘法性能测试

同上方案测试IQmath库乘法运行的性能

		_iq22 A = _IQ22(1.2f);
		_iq22 B = _IQ22(1.11f);
		_iq22 mul = 0;
		
		while(1)
		{
			std_gpio_set_pin(GPIOB,GPIO_PIN_0);//引脚上拉
			mul = _IQ22mpy(A, B);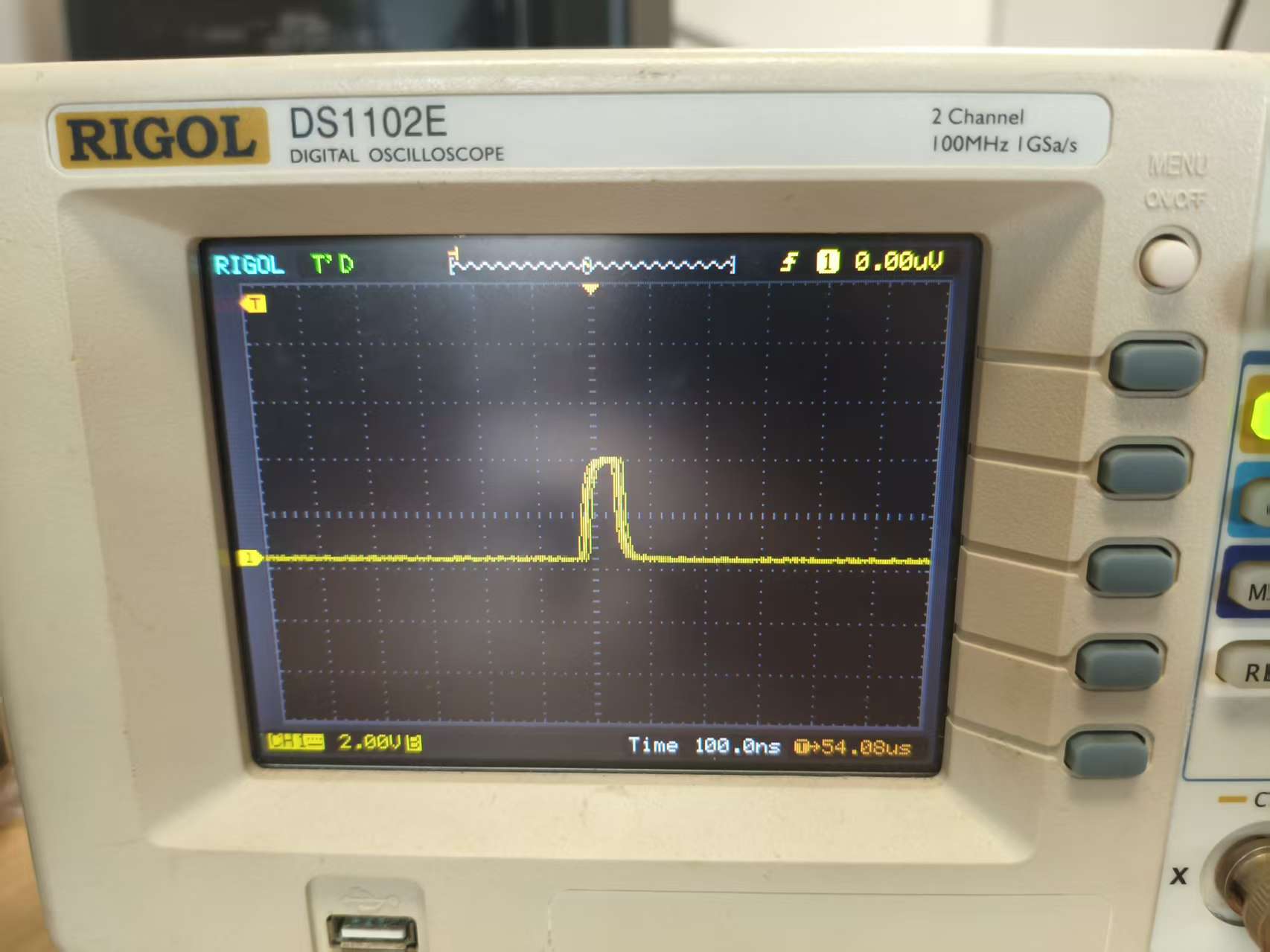![请添加图片描述](https://i-blog.csdnimg.cn/direct/f7995afa474b45b6a37f1e79b5a538ee.jpeg)

			std_gpio_reset_pin(GPIOB,GPIO_PIN_0);//引脚下拉
			std_delayus(5);//延迟
		} 

从下图可评估处，运行一次乘法运算(包含乘法和缩放的计算),需要约2.5us

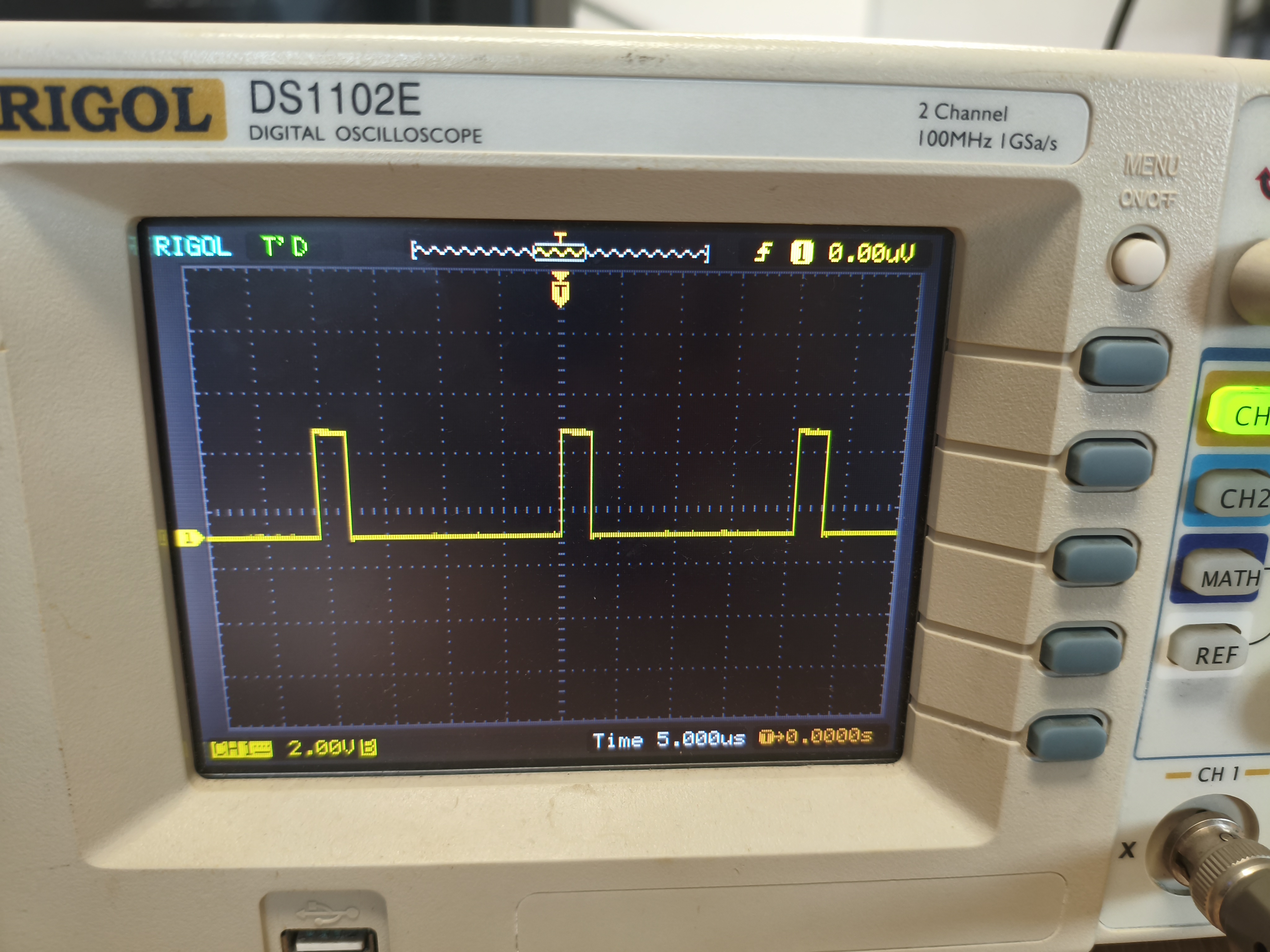
为了更严谨地评估，我们将测试范围拓展到运行100次乘法运算需要消耗多少时间

		_iq22 A = _IQ22(1.2f);
		_iq22 B = _IQ22(1.11f);
		_iq22 mul = 0;
	  	uint32_t i;

		while(1)
		{
			std_gpio_set_pin(GPIOB,GPIO_PIN_0);//引脚上拉
			for(i = 0;i < 100; i++)
			{
				mul = _IQ22mpy(A, B);
			}
			std_gpio_reset_pin(GPIOB,GPIO_PIN_0);//引脚下拉
			std_delayus(5);//延迟
			
		} 

运行100次乘法运算(包含乘法和缩放的计算),需要约260us

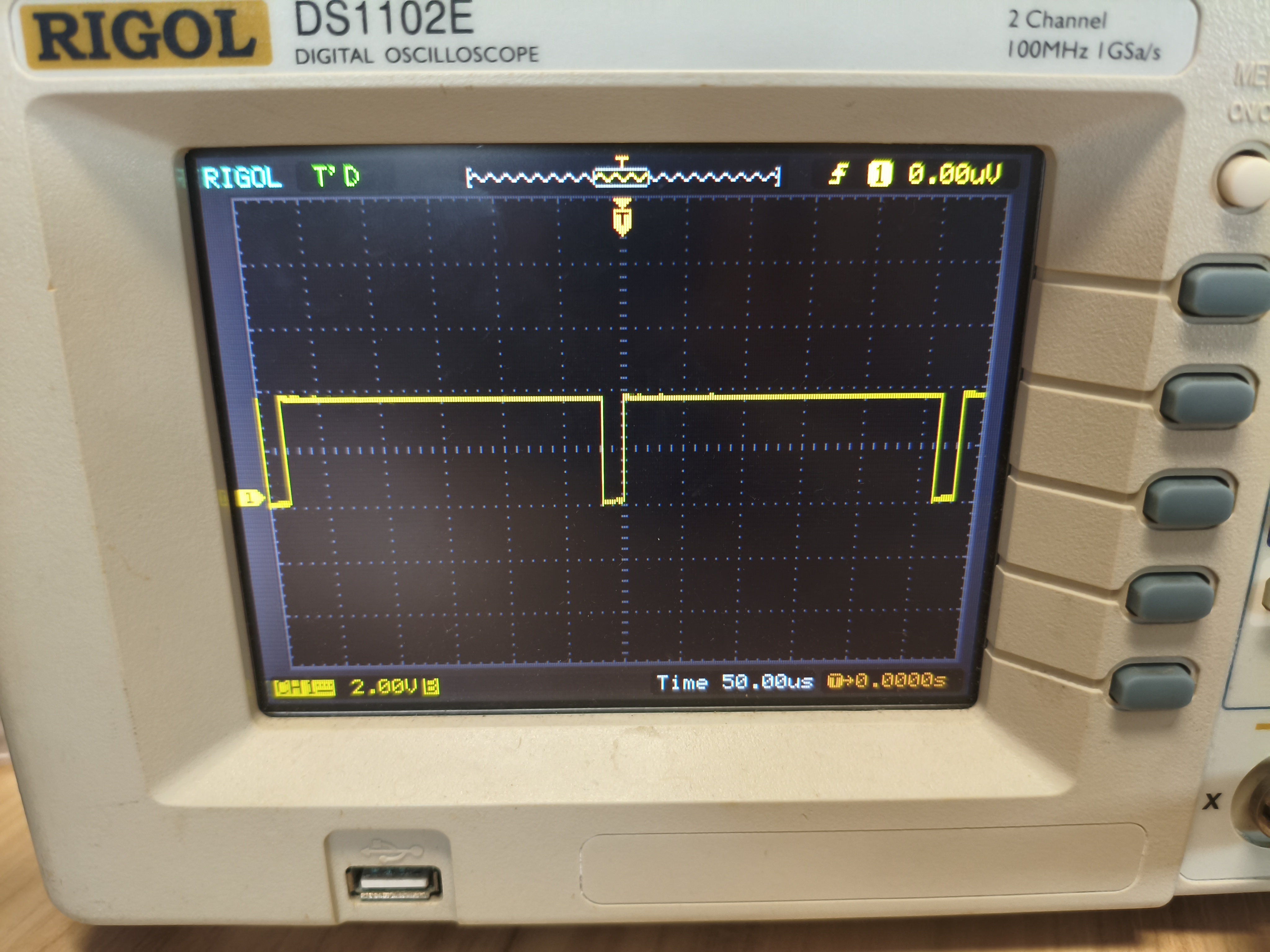
八、原生计算float乘法性能测试

测试单次float乘法所需时间

		float A = 1.2f;
		float B = 1.11f;
		float mul = 0.0f;
	 
		while(1)
		{
			std_gpio_set_pin(GPIOB,GPIO_PIN_0);//引脚上拉
			mul = A * B;
			std_gpio_reset_pin(GPIOB,GPIO_PIN_0);//引脚下拉
			std_delayus(5);//延迟
		} 

运行一次float乘法约需90ns

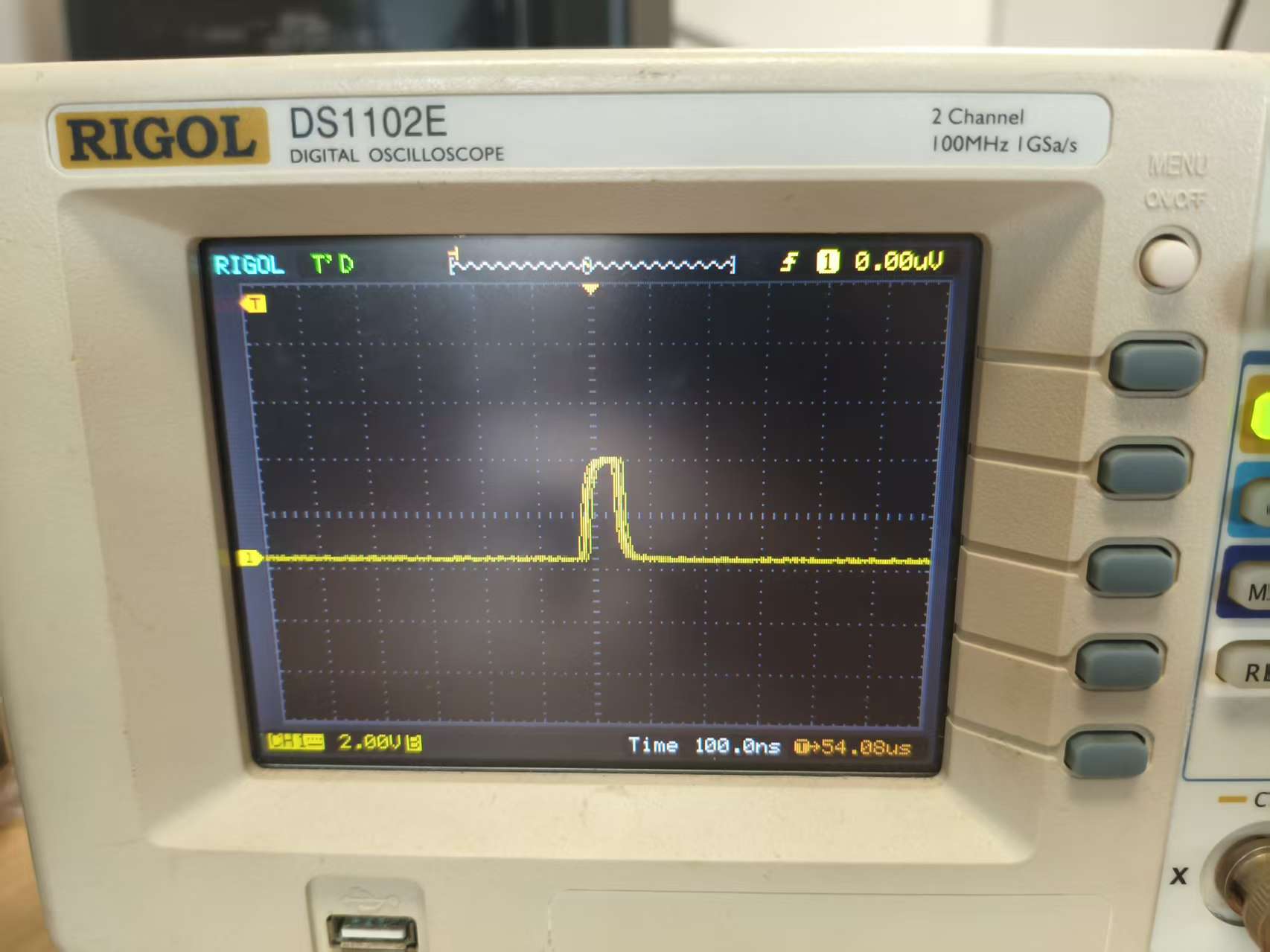
测试范围运行100次乘法运算需要消耗多少时间

		float A = 1.2f;
		float B = 1.11f;
		float mul = 0.0f;
	 	uint32_t i;

		while(1)
		{
			std_gpio_set_pin(GPIOB,GPIO_PIN_0);//引脚上拉
			for(i = 0;i < 100; i++)
			{
				mul = A * B;
			}
			std_gpio_reset_pin(GPIOB,GPIO_PIN_0);//引脚下拉
			std_delayus(5);//延迟
		} 

运行100次乘法运算,需要约12.5us

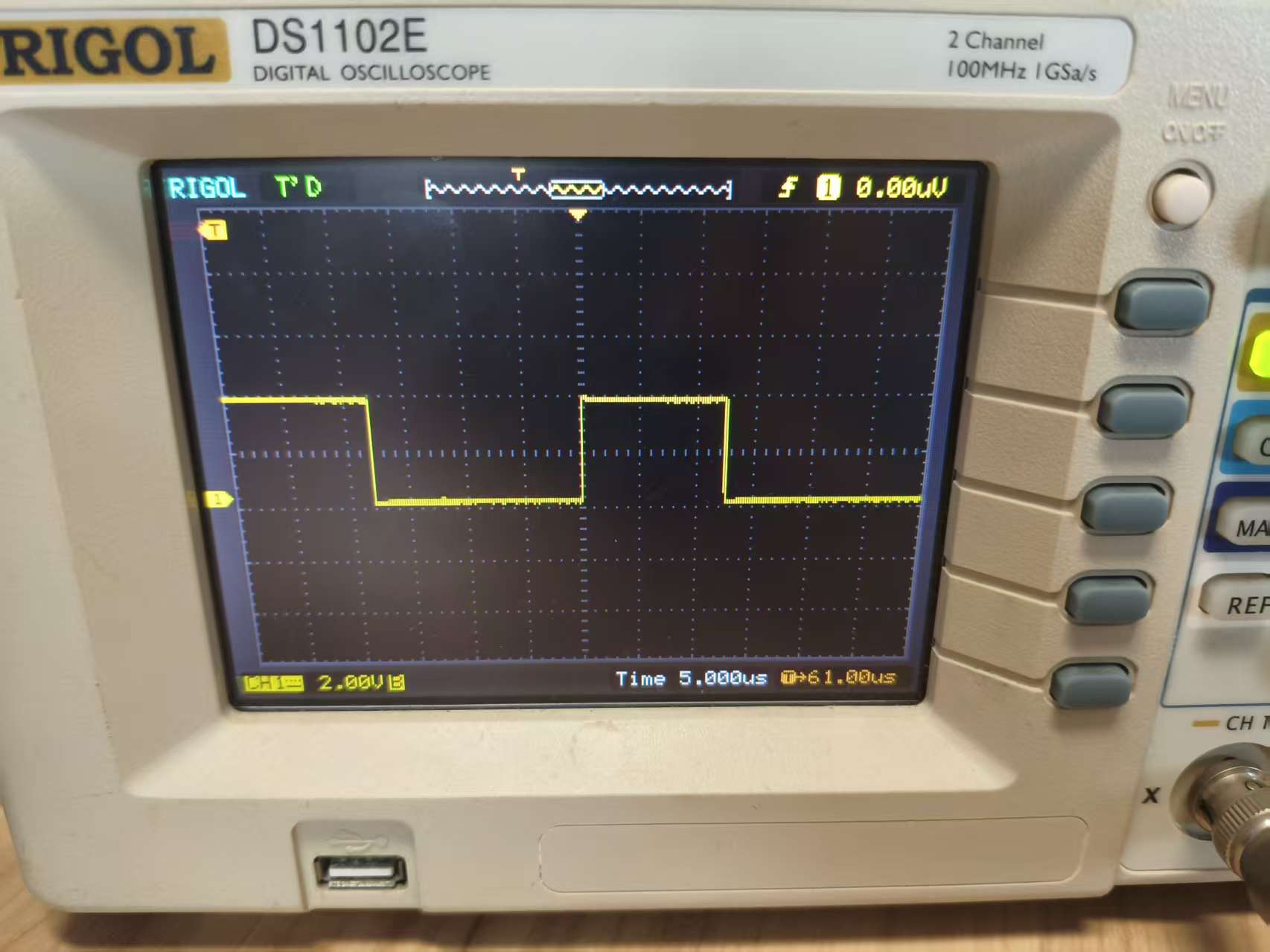
九、性能对比表

平台	CIU32F003
核心	32 位 ARM Cortex-M0+ 微控制器
FPU加速	无
IDE	KEIL
语言	C
代码优化	Level3(-O3)
代码位置	主循环
测试方法	GPIO翻转
[测试环境]

方法/库	单次乘法耗时	100次乘法耗时
FR_math 定点库	< 1.5 µs	150 µs
IQmath 定点库	2.5 µs	260 µs
原生 float 运算	90 ns	12.5 µs
[不同库/方法乘法耗时对比]

十、某保密算法的性能测试对比

平台	CIU32F003
核心	32 位 ARM Cortex-M0+ 微控制器
FPU加速	无
IDE	KEIL
语言	C
代码位置	中断
测试方法	GPIO翻转
[测试环境]

方法/库	O0优化 单次中断算法耗时	O3优化 单次中断算法耗时
FR_math 定点库	\	\
IQmath 定点库	30 us ~ 45us	24 us ~ 35us
原生 float 运算	26 us ~ 39us	24 us ~ 35us
[算法耗时对比]

方法/库	O3优化 单次中断算法耗时
FR_math 定点库	\
IQmath 定点库	14us ~22us
原生 float 运算	21us~31us
[优化后算法耗时对比]

十一、总结

在CIU32F003平台下（无硬件FPU加速支持）：

1、简单的浮点运算中，虽然没有FPU加速，原生的float运算仍能表现出较优性能；

2、执行更复杂的算法运算时，原生float的性能衰减可能更为明显；

3、根据需要执行的算法复杂度，浮点转定点计算的性能可能更有更优，但也有可能不如直接执行原生的float运算，需根据不同场景细分优化；

4、在大批量浮点运算，没有频繁将浮点转回定点的场景下，更推荐使用定点算法；

5、在小批量的浮点运算情况下，原生float性能可能表现更好；