1 题目
给你一个整数数组 nums 。
如果一组数字 (i,j) 满足 nums[i] == nums[j] 且 i < j ,就可以认为这是一组 好数对 。
返回好数对的数目。
示例 1:
输入:nums = [1,2,3,1,1,3]
输出:4
解释:有 4 组好数对,分别是 (0,3), (0,4), (3,4), (2,5) ,下标从 0 开始示例 2:
输入:nums = [1,1,1,1]
输出:6
解释:数组中的每组数字都是好数对示例 3:
输入:nums = [1,2,3]
输出:0提示:
1 <= nums.length <= 1001 <= nums[i] <= 100
2 代码实现
cpp
class Solution {
public:
int numIdenticalPairs(vector<int>& nums) {
int count = 0;
int n = nums.size();
for(int i = 0; i < n ; i ++){
for (int j = n - 1 ; j > i ;j--){
if(nums[i] == nums[j]){
count++;
}
}
}
return count;
}
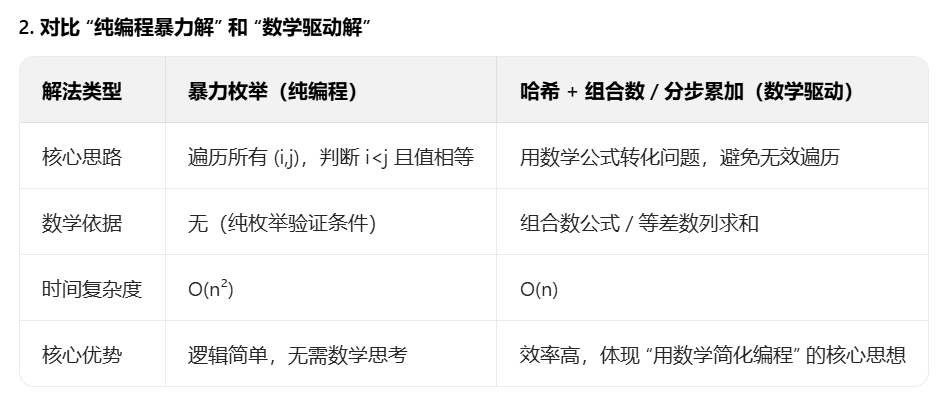
};暴力枚举的做法,通过了,但是我知道这肯定不是好的做法。
好的做法难道是哈希映射吗,怎么做呢?
3 优化实现
优化思路:哈希统计 + 组合数计算

这个思路的时间复杂度是 (O(n))(仅需遍历数组两次:一次统计、一次计算),空间复杂度(O(1))(因为数值范围固定为 1~100,数组大小固定)。
优化代码实现
cpp
class Solution {
public:
int numIdenticalPairs(vector<int>& nums) {
// 用数组代替哈希表(数值范围1~100,索引0不用)
int count[101] = {0};
int res = 0;
// 第一步:统计每个数字出现的次数
for (int num : nums) {
count[num]++;
}
// 第二步:计算每个数字的组合数并累加
for (int cnt : count) {
// 只有出现次数≥2的数字才会产生好数对
if (cnt >= 2) {
res += cnt * (cnt - 1) / 2;
}
}
return res;
}
};代码解释
- 统计次数 :遍历数组
nums,用count[num]记录每个数字num出现的次数(比如示例 1 中,1 出现 3 次、3 出现 2 次、2 出现 1 次); - 计算组合数 :
- 数字 1 出现 3 次:组合数 = \(3×2/2 = 3\)(对应下标 0-3、0-4、3-4);
- 数字 3 出现 2 次:组合数 = \(2×1/2 = 1\)(对应下标 2-5);
- 数字 2 出现 1 次:无组合数;
- 总和 \(3+1=4\),与示例 1 结果一致。
进一步简化(一次遍历)
可以在统计次数的同时直接计算结果,无需二次遍历:
cpp
class Solution {
public:
int numIdenticalPairs(vector<int>& nums) {
int count[101] = {0};
int res = 0;
for (int num : nums) {
// 每新增一个num,能和之前已出现的count[num]个num组成新的好数对
res += count[num]++;
}
return res;
}
};

逻辑说明 :比如数字 1 依次出现,第一次 count[1]=0(无贡献),第二次 count[1]=1(贡献 1),第三次 count[1]=2(贡献 2),总贡献 (0+1+2=3),和组合数公式结果一致。
这种方式既节省空间(无需额外存储),又减少遍历次数,是最优解。
4 题目
给你一个 不包含 任何零的整数数组 nums ,找出自身与对应的负数都在数组中存在的最大正整数 k 。
返回正整数k ,如果不存在这样的整数,返回 -1 。
示例 1:
输入:nums = [-1,2,-3,3]
输出:3
解释:3 是数组中唯一一个满足题目要求的 k 。示例 2:
输入:nums = [-1,10,6,7,-7,1]
输出:7
解释:数组中存在 1 和 7 对应的负数,7 的值更大。示例 3:
输入:nums = [-10,8,6,7,-2,-3]
输出:-1
解释:不存在满足题目要求的 k ,返回 -1 。提示:
1 <= nums.length <= 1000-1000 <= nums[i] <= 1000nums[i] != 0
5 代码实现
cpp
class Solution {
public:
int findMaxK(vector<int>& nums) {
int k = -1 ;
int n = nums.size();
for (int i = 0 ; i < n ; i++ ){
for (int j = n -1 ; j > i ; j--){
if (nums[i] + nums[j] == 0 ){
int current = max(nums[i] , nums[j]);
k = current > k ? current : k;
}
}
}
return k;
}
};通过了,但是充满了bad cases ,看看哪里可以优化一下吧。
一、当前代码的核心问题
1. 逻辑冗余:max(nums[i], nums[j]) 可简化
当 nums[i] + nums[j] = 0 时,两者互为相反数,比如 3 和 -3,max 结果就是正数的那个,直接用 abs(nums[i]) 更简洁,逻辑也更直观。
2. 效率问题:找到符合条件的数后,未及时终止内层循环(非错误,但可优化)
比如数组是 [-3,2,-1,3],当 i=0、j=3 时已经找到 3 和 -3,此时内层循环还会继续检查 j=2、j=1(无意义),可以提前 break 减少遍历次数。
3. 边界场景:数组含 0 时不会误判(当前代码已规避)
因为 0+0=0,但内层循环 j>i 保证了 i≠j,所以单个 0 或多个 0 不会被误判为有效 k,这一点是正确的。
二、修正并优化后的代码
cpp
class Solution {
public:
int findMaxK(vector<int>& nums) {
int k = -1;
int n = nums.size();
for (int i = 0; i < n; i++) {
for (int j = n - 1; j > i; j--) { // 从后往前遍历,j>i避免重复检查
if (nums[i] + nums[j] == 0) {
int current = abs(nums[i]); // 简化max逻辑
if (current > k) {
k = current;
}
break; // 找到当前i对应的最大j,无需继续遍历更小的j
}
}
}
return k;
}
};三、测试用例验证
测试用例 1:常规场景
输入:nums = [-1,2,-3,3]执行过程:
i=0(nums [i]=-1):j 从 3→1,无符合条件的数;i=1(nums [i]=2):j 从 3→2,无符合条件的数;i=2(nums [i]=-3):j=3(nums [j]=3),满足-3+3=0,current=3,k 更新为 3;最终返回3(正确)。
测试用例 2:无有效 k 的场景
输入:nums = [-10,8,6,7,-2,-3]执行过程:所有 i/j 组合都不满足 nums[i]+nums[j]=0,k 保持 -1(正确)。
测试用例 3:多个有效 k 的场景
输入:nums = [-5,5,-3,3,-2,2]执行过程:
i=0(-5)→j=1(5),current=5,k=5;- 后续 i=2(-3)→j=3(3),current=3(小于 5,k 不变);
- i=4(-2)→j=5(2),current=2(小于 5,k 不变);最终返回
5(正确)。
四、进阶优化(时间复杂度从 O (n²)→O (n))
如果想进一步提升效率,推荐用哈希集合(空间换时间),遍历每个正数,检查其相反数是否存在,直接找最大值:
cpp
class Solution {
public:
int findMaxK(vector<int>& nums) {
int k = -1;
unordered_set<int> num_set(nums.begin(), nums.end());
for (int num : nums) {
if (num > 0 && num_set.count(-num)) { // 只检查正数,避免重复判断
k = max(k, num);
}
}
return k;
}
};总结
- 若追求简洁:用
abs(nums[i])替代max(nums[i], nums[j]); - 若追求效率:优先选择哈希集合解法(O (n) 时间复杂度)。