目录
[1. 颜色分类](#1. 颜色分类)
[1.1 解题思路](#1.1 解题思路)
[1.2 代码实现](#1.2 代码实现)
[2. 排序数组](#2. 排序数组)
[2.1 解题思路](#2.1 解题思路)
[2.2 代码实现](#2.2 代码实现)
[3.1 解题思路](#3.1 解题思路)
[3.2 代码实现](#3.2 代码实现)
[4.1 解题思路](#4.1 解题思路)
[4.2 代码实现](#4.2 代码实现)
[5. 排序数组(归并排序)](#5. 排序数组(归并排序))
[5.1 解题思路](#5.1 解题思路)
[5.2 代码实现](#5.2 代码实现)
[6. 交易逆序对的总数](#6. 交易逆序对的总数)
[6.1 解题思路](#6.1 解题思路)
[6.2 代码实现](#6.2 代码实现)
[7. 计算右侧小于当前元素的个数](#7. 计算右侧小于当前元素的个数)
[7.1 解题思路](#7.1 解题思路)
[7.2 代码实现](#7.2 代码实现)
[8. 翻转对](#8. 翻转对)
[8.1 解题思路编辑](#8.1 解题思路编辑)
[8.2 代码实现](#8.2 代码实现)
1. 颜色分类
1.1 解题思路

1.2 代码实现
java
class Solution {
public void sortColors(int[] nums) {
int left = -1;
int right = nums.length;
int i = 0;
while(i < right) {
if(nums[i] == 0) {
swap(nums,++left,i++);
}else if(nums[i] == 1) {
i++;
}else {
swap(nums,--right,i);
}
}
}
public void swap(int[] nums, int i, int j) {
int tmp = nums[i];
nums[i] = nums[j];
nums[j] = tmp;
}
}2. 排序数组
2.1 解题思路

2.2 代码实现
java
class Solution {
public int[] sortArray(int[] nums) {
recursion(nums,0,nums.length-1);
return nums;
}
public void recursion(int[] nums, int l, int r) {
if(l >= r) {
return;
}
//利用数组分三部分来排序
int ran = nums[new Random().nextInt(r-l+1) + l];
int left = l - 1;
int right = r + 1;
int i = l;
while(i < right) {
if(nums[i] < ran) {
swap(nums,++left,i++);
}else if(nums[i] == ran) {
i++;
}else {
swap(nums,--right,i);
}
}
//[l,left] [left+1,right-1] [right,r]
recursion(nums,l,left);
recursion(nums,right,r);
}
public void swap(int[] nums, int i, int j) {
int tmp = nums[i];
nums[i] = nums[j];
nums[j] = tmp;
}
}3.数组中的第K个最大元素
3.1 解题思路
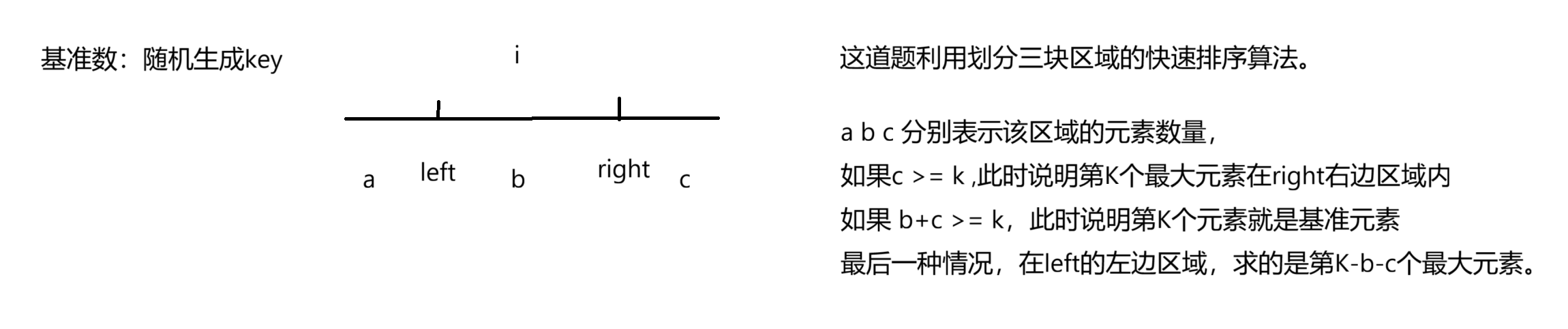
3.2 代码实现
java
class Solution {
public int findKthLargest(int[] nums, int k) {
return quickSort(nums,0,nums.length - 1,k);
}
public int quickSort(int[] nums, int l, int r, int k) {
if(l == r) {
return nums[l];
}
int left = l-1;
int right = r+1;
int i = l;
int ran = nums[new Random().nextInt(r-l+1) + l];
while(i < right) {
if(nums[i] < ran) {
swap(nums,++left,i++);
}else if(nums[i] == ran) {
i++;
}else {
swap(nums,--right,i);
}
}
//进行筛选范围查找
int b = right - left - 1;
int c = r - right + 1;
if(c >= k) {
return quickSort(nums,right,r,k);
}else if(b+c >= k) {
return ran;
}else {
return quickSort(nums,l,left,k-b-c);
}
}
public void swap(int[] nums, int i, int j) {
int tmp = nums[i];
nums[i] = nums[j];
nums[j] = tmp;
}
}4.库存管理3
4.1 解题思路

4.2 代码实现
java
class Solution {
public int[] inventoryManagement(int[] stock, int cnt) {
//把前K小个元素提取到前面
quickSort(stock,0,stock.length-1,cnt);
int[] arr = new int[cnt];
for(int i = 0; i < cnt; i++) {
arr[i] = stock[i];
}
return arr;
}
public void quickSort(int[] stock, int l, int r, int cnt) {
if(l == r) {
return;
}
int left = l - 1;
int right = r + 1;
int i = l;
int ran = stock[new Random().nextInt(r-l+1) + l];
while(i < right) {
if(stock[i] < ran) {
swap(stock,++left,i++);
}else if(stock[i] == ran) {
i++;
}else {
swap(stock,--right,i);
}
}
int a = left - l + 1;
int b = right - left - 1;
if(a > cnt) {
quickSort(stock,l,left,cnt);
}else if(a+b >= cnt) {
return;
}else {
quickSort(stock,right,r,cnt-a-b);
}
}
public void swap(int[] stock, int i, int j) {
int tmp = stock[i];
stock[i] = stock[j];
stock[j] = tmp;
}
}5. 排序数组(归并排序)
5.1 解题思路

5.2 代码实现
java
class Solution {
int[] tmp;
public int[] sortArray(int[] nums) {
tmp = new int[nums.length + 1];
mergeSort(nums,0,nums.length-1);
return nums;
}
public void mergeSort(int[] nums, int left, int right) {
if(left >= right) {
return;
}
int mid = left + (right - left) / 2;
//将左边部分排序
mergeSort(nums,left,mid);
//将右边部分排序
mergeSort(nums,mid+1,right);
//合并两个有序数组
int cur1 = left;
int cur2 = mid + 1;
int k = 0;
while(cur1 <= mid && cur2 <= right) {
tmp[k++] = nums[cur1] > nums[cur2] ? nums[cur2++] : nums[cur1++];
}
//处理数组剩余元素
while(cur1 <= mid) tmp[k++] = nums[cur1++];
while(cur2 <= right) tmp[k++] = nums[cur2++];
//更新原数组
for(int i = left; i <= right; i++) {
nums[i] = tmp[i - left];
}
}
}6. 交易逆序对的总数
6.1 解题思路
利用了归并排序的思路,可以提高效率。
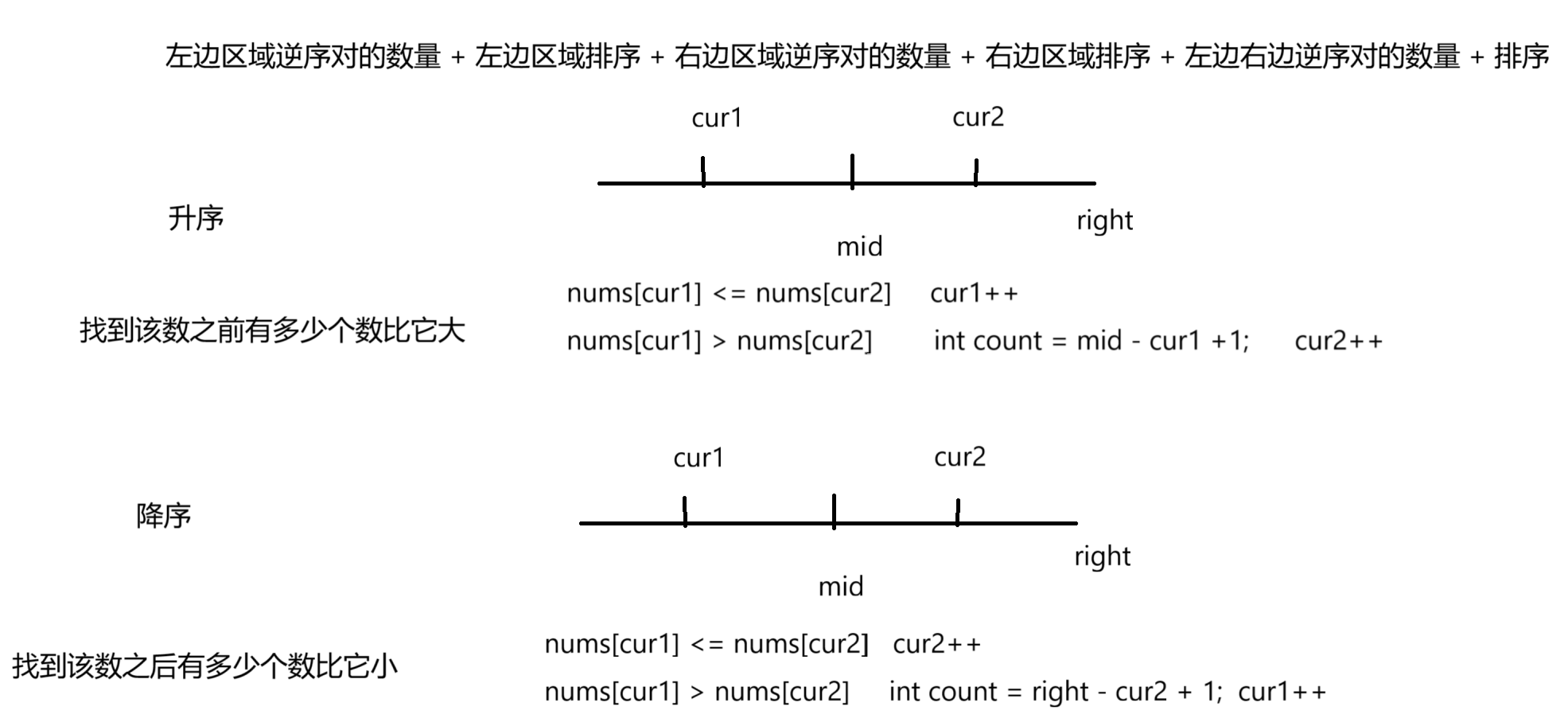
6.2 代码实现
升序代码:
java
class Solution {
int[] tmp;
public int reversePairs(int[] record) {
tmp = new int[record.length];
return mergeSort(record,0,record.length - 1);
}
public int mergeSort(int[] record, int left, int right) {
if(left >= right) {
return 0;
}
int mid = left + (right - left)/ 2;
int leftNum = mergeSort(record, left, mid);
int rightNum = mergeSort(record, mid + 1, right);
int cur1 = left;
int cur2 = mid + 1;
int i = 0;
int count = 0;
while(cur1 <= mid && cur2 <= right) {
if(record[cur1] <= record[cur2]) {
tmp[i++] = record[cur1++];
}else {
count += mid - cur1 + 1;
tmp[i++] = record[cur2++];
}
}
while(cur1 <= mid) tmp[i++] = record[cur1++];
while(cur2 <= right) tmp[i++] = record[cur2++];
for(int k = left; k <= right; k++) {
record[k] = tmp[k - left];
}
return leftNum + rightNum + count;
}
}降序代码:
java
class Solution {
int[] tmp;
public int reversePairs(int[] record) {
int len = record.length;
tmp = new int[len];
return mergeSort(record,0,len-1);
}
public int mergeSort(int[] nums, int left, int right) {
if(left >= right) {
return 0;
}
int mid = left + (right - left) / 2;
int count = 0;
count += mergeSort(nums,left,mid);
count += mergeSort(nums,mid+1,right);
int cur1 = left;
int cur2 = mid + 1;
int i = 0;
while(cur1 <= mid && cur2 <= right) {
if(nums[cur1] <= nums[cur2]) {
tmp[i++] = nums[cur2++];
}else {
count += right - cur2 + 1;
tmp[i++] = nums[cur1++];
}
}
while(cur1 <= mid) tmp[i++] = nums[cur1++];
while(cur2 <= right) tmp[i++] = nums[cur2++];
for(int k = left; k <= right; k++) {
nums[k] = tmp[k - left];
}
return count;
}
}7. 计算右侧小于当前元素的个数
7.1 解题思路
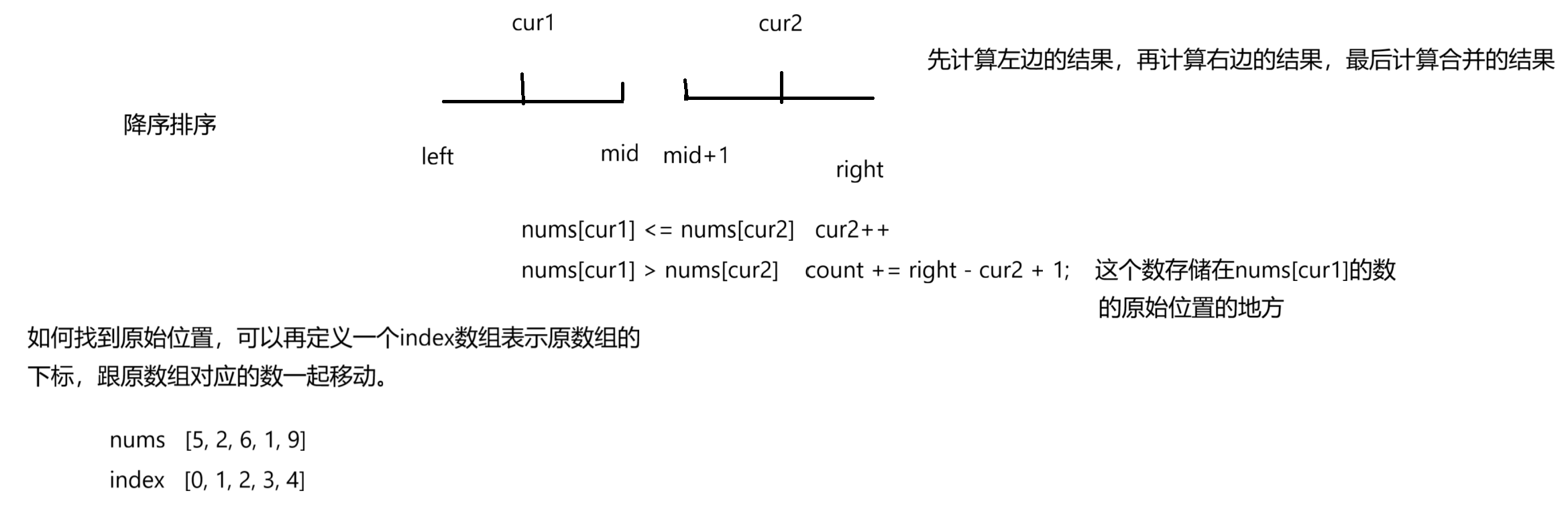
7.2 代码实现
java
class Solution {
//结果数组
int[] ret;
int[] tmpNums;
int[] tmpIndex;
int[] index;
public List<Integer> countSmaller(int[] nums) {
int len = nums.length;
ret = new int[len];
tmpNums = new int[len];
tmpIndex = new int[len];
index = new int[len];
//初始化index数组
for (int i = 0; i < len; i++) {
index[i] = i;
}
mergeSort(nums, 0, len - 1);
List<Integer> list = new ArrayList<>();
for (int x : ret) {
list.add(x);
}
return list;
}
public void mergeSort(int[] nums, int left, int right) {
if (left >= right) {
return;
}
int mid = left + (right - left) / 2;
//处理左右两边的情况。
mergeSort(nums, left, mid);
mergeSort(nums, mid + 1, right);
int cur1 = left;
int cur2 = mid + 1;
int i = 0;
while (cur1 <= mid && cur2 <= right) {
if (nums[cur1] <= nums[cur2]) {
tmpNums[i] = nums[cur2];
tmpIndex[i++] = index[cur2++];
} else {
ret[index[cur1]] += right - cur2 + 1;
tmpNums[i] = nums[cur1];
tmpIndex[i++] = index[cur1++];
}
}
while (cur1 <= mid) {
tmpNums[i] = nums[cur1];
tmpIndex[i++] = index[cur1++];
}
while (cur2 <= right) {
tmpNums[i] = nums[cur2];
tmpIndex[i++] = index[cur2++];
}
for(int k = left; k <= right; k++) {
nums[k] = tmpNums[k - left];
index[k] = tmpIndex[k - left];
}
}
}8. 翻转对
8.1 解题思路
8.2 代码实现
java
class Solution {
int[] tmp;
public int reversePairs(int[] nums) {
int len = nums.length;
tmp = new int[len];
return mergeSort(nums, 0, len - 1);
}
public int mergeSort(int[] nums, int left, int right) {
if(left >= right) {
return 0;
}
int mid = left + (right - left) / 2;
int count = 0;
count += mergeSort(nums, left, mid);
count += mergeSort(nums, mid + 1, right);
int cur1 = left;
int cur2 = mid + 1;
while(cur1 <= mid) {
while(cur2 <= right && nums[cur1] / 2.0 <= nums[cur2]) cur2++;
if(cur2 > right) {
break;
}
count += right - cur2 + 1;
cur1++;
}
cur1 = left;
cur2 = mid + 1;
int i = 0;
while(cur1 <= mid && cur2 <= right) {
if(nums[cur1] <= nums[cur2]) {
tmp[i++] = nums[cur2++];
}else {
tmp[i++] = nums[cur1++];
}
}
while(cur1 <= mid) tmp[i++] = nums[cur1++];
while(cur2 <= right) tmp[i++] = nums[cur2++];
for(int k = left; k <= right; k++) {
nums[k] = tmp[k - left];
}
return count;
}
}