进阶数据结构-AC自动机

Ayanami_Reii2025-12-07 13:24

目录

算法能解决的问题

给定 n n n个模式串, 给定主串 s s s, 非常高的效率检查主串 s s s中是否存在某个模式串

算法原理

AC自动机本质是在Trie树上用KMP算法的思想的结果

假设在Trie 插入如下模式串she, he, say, shr, her

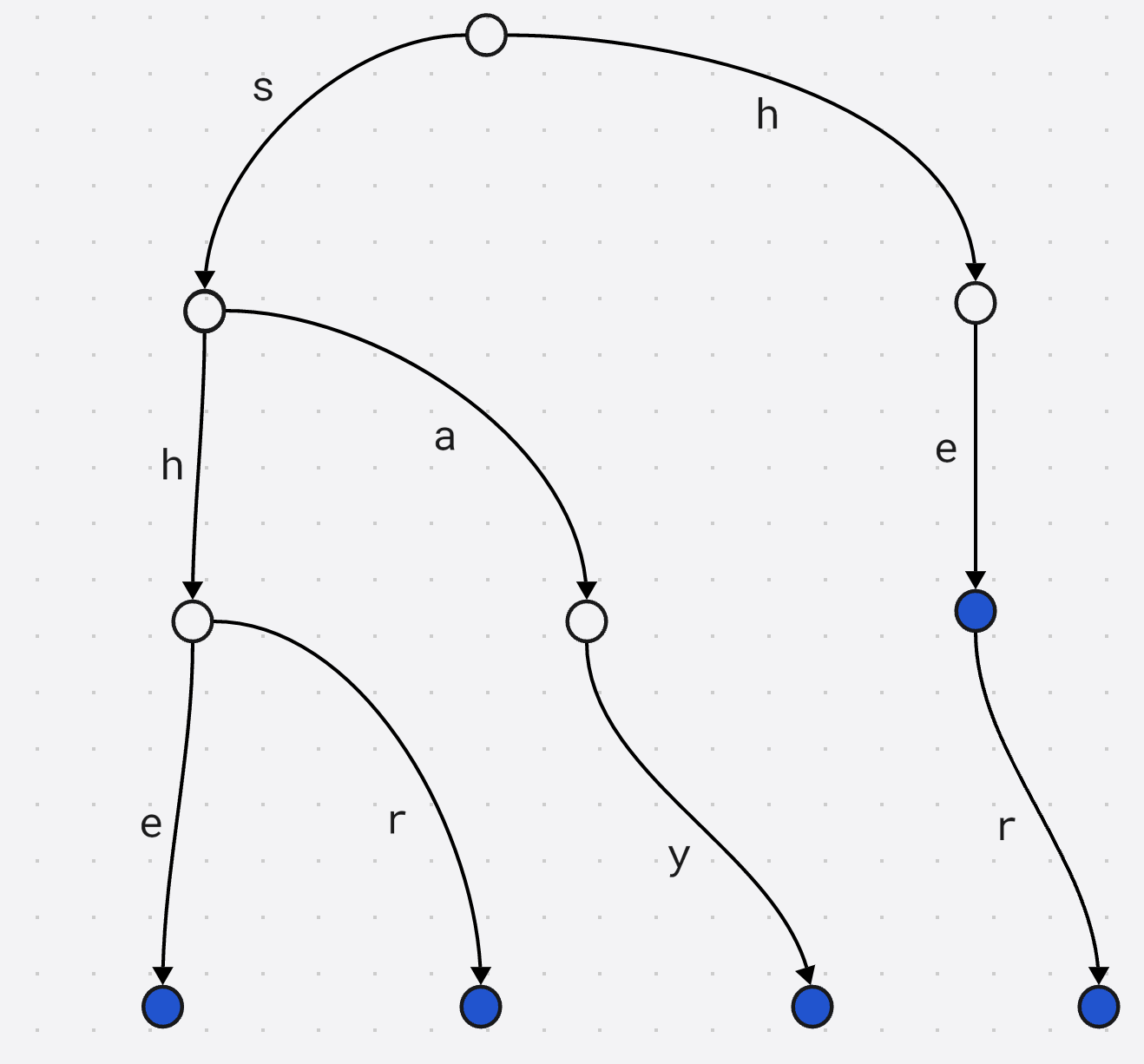
将KMP算法的ne数组类比到AC自动机中

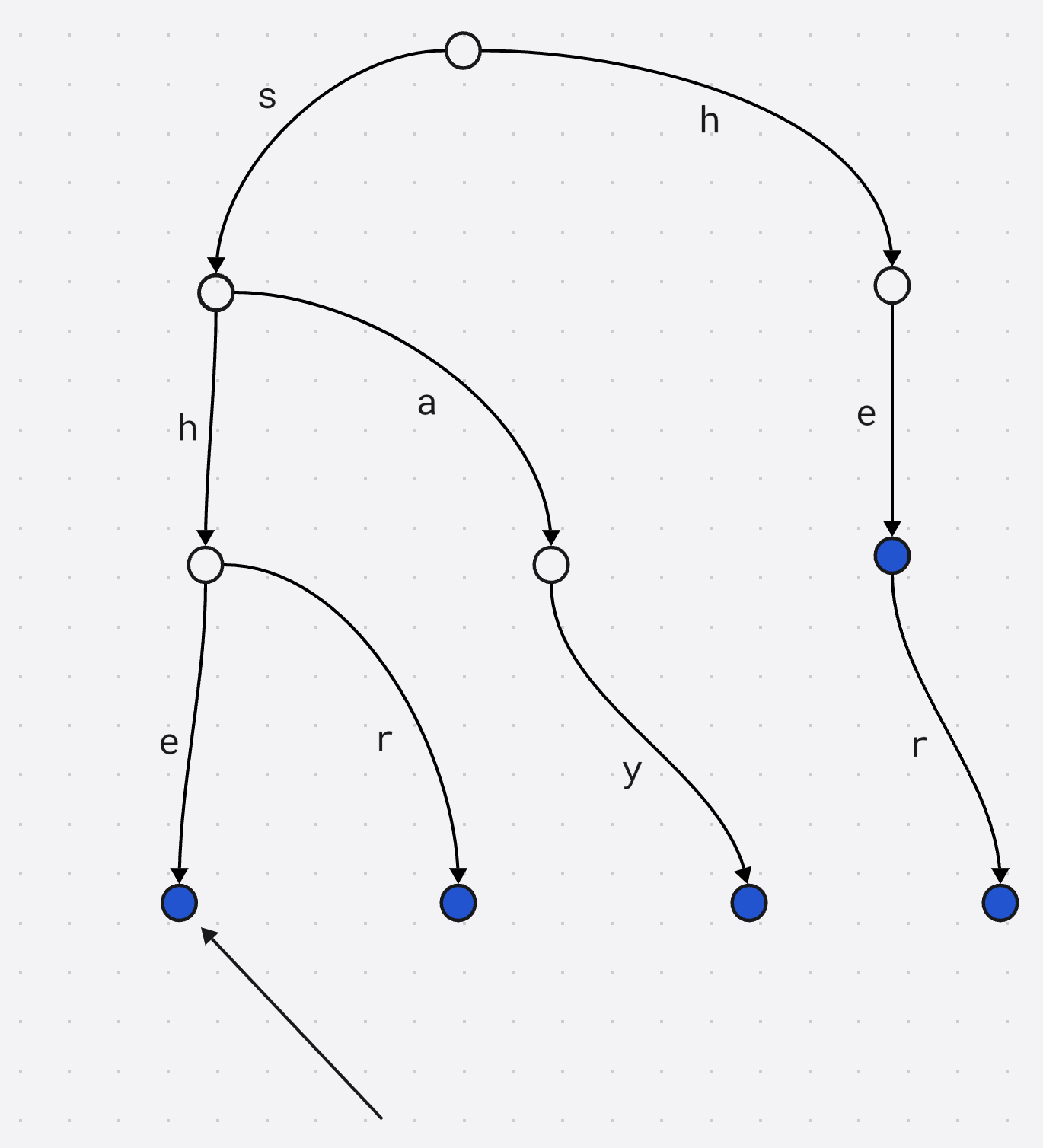
假设考虑当前子串she, 节点 e e e存储的是以 e e e结尾的某个后缀(后缀有e, he), 和某个最长真前缀 匹配的最长前缀的结尾下标

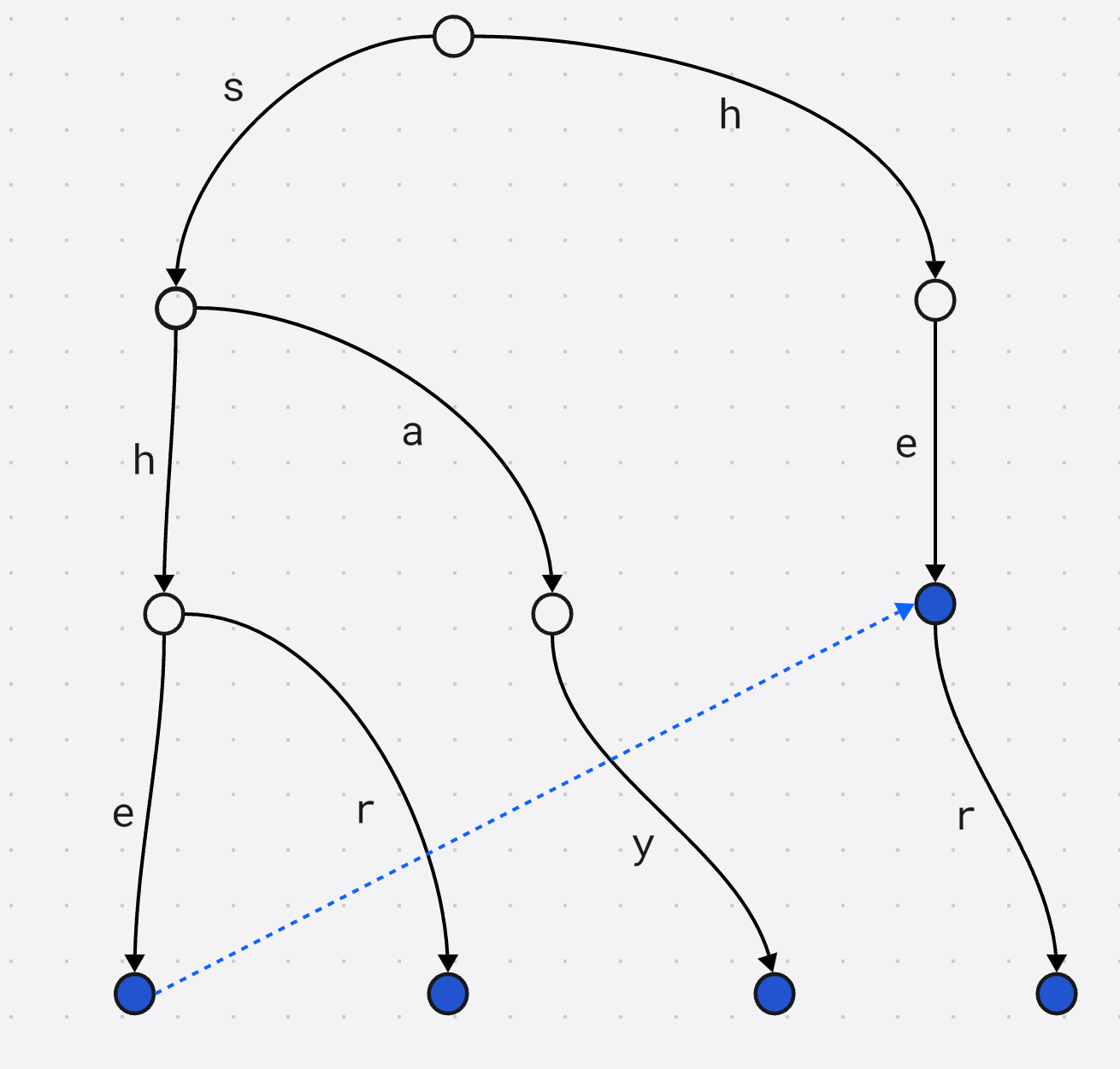
在上述Trie树中, she的最长匹配真前缀 在 h e he he的结尾

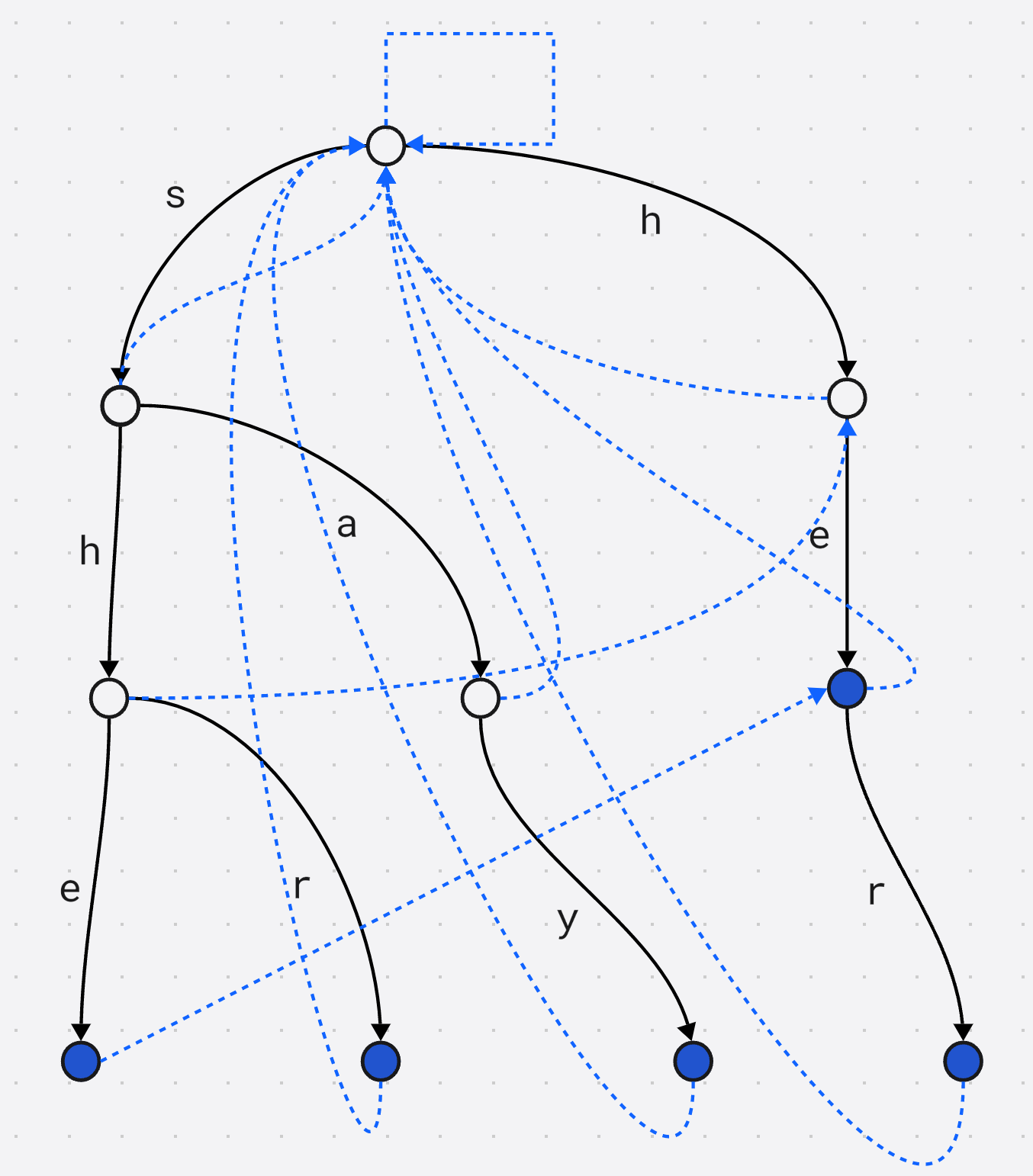
上图是样例构建出AC自动机后的情况

问题就变成了如何计算这些指针 ?

因为KMP算法计算ne数组的过程是根据 [ 0 , i − 1 ] [0, i - 1] [0,i−1]的ne值递推出来的

类比于KMP算法计算ne数组的过程

  • 计算AC自动机的fail数组, 用 b f s bfs bfs搜索 , 将 u u u视为上一层 , 当前层是 t r [ u ] [ i ] tr[u][i] tr[u][i]
  • j = fail[u]就类比于KMP算法的j = ne[i - 1]
  • 然后向前找, 如果失败j = fail[j], 类比到KMP算法, j = ne[j - 1]或者j = ne[j], 两种写法都是对的, 只不过初始下标不同
  • 如果找到了匹配的位置if (tr[j][i]), 那么j = tr[j][i], 类比到KMP算法if (s[j] == s[i]) j++或者if (s[j + 1] == s[i]) j++
  • 然后记录当前fail值, fail[c] = j, 类比于KMP算法ne[i] = j

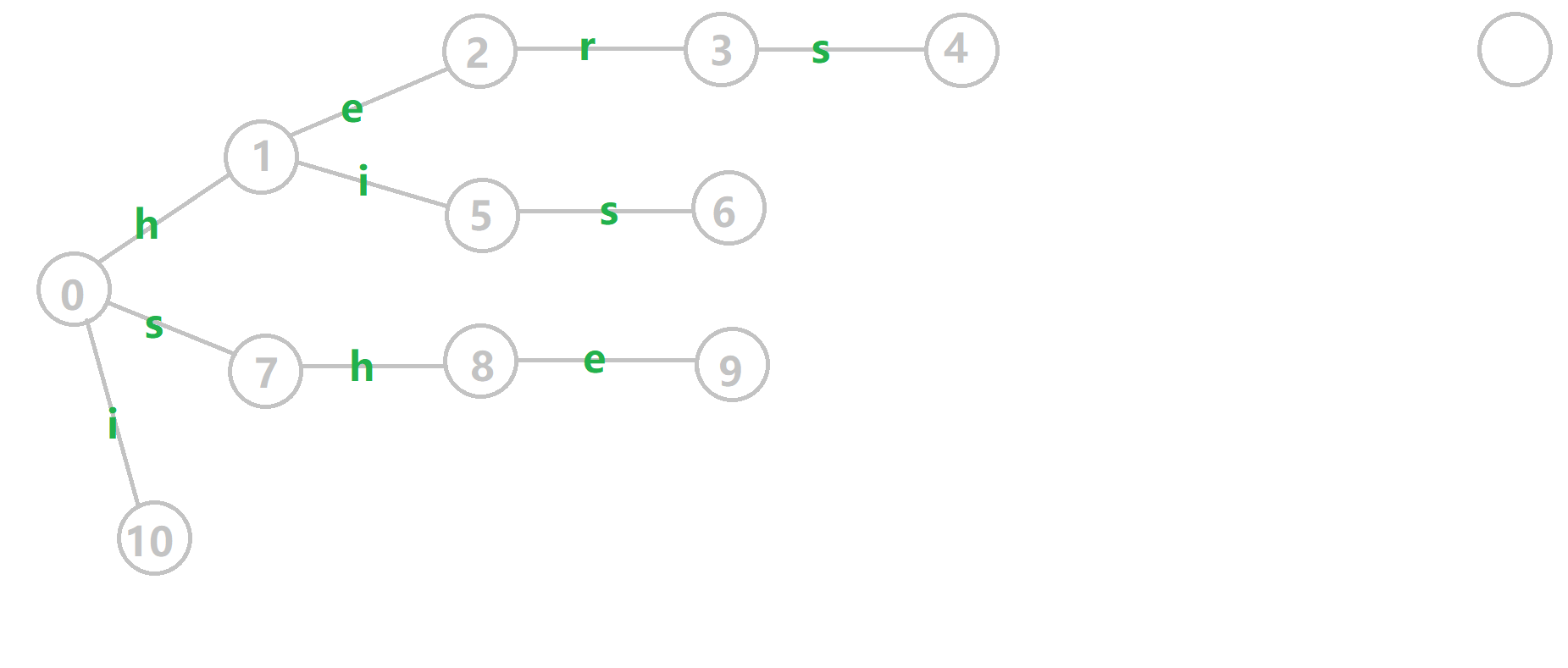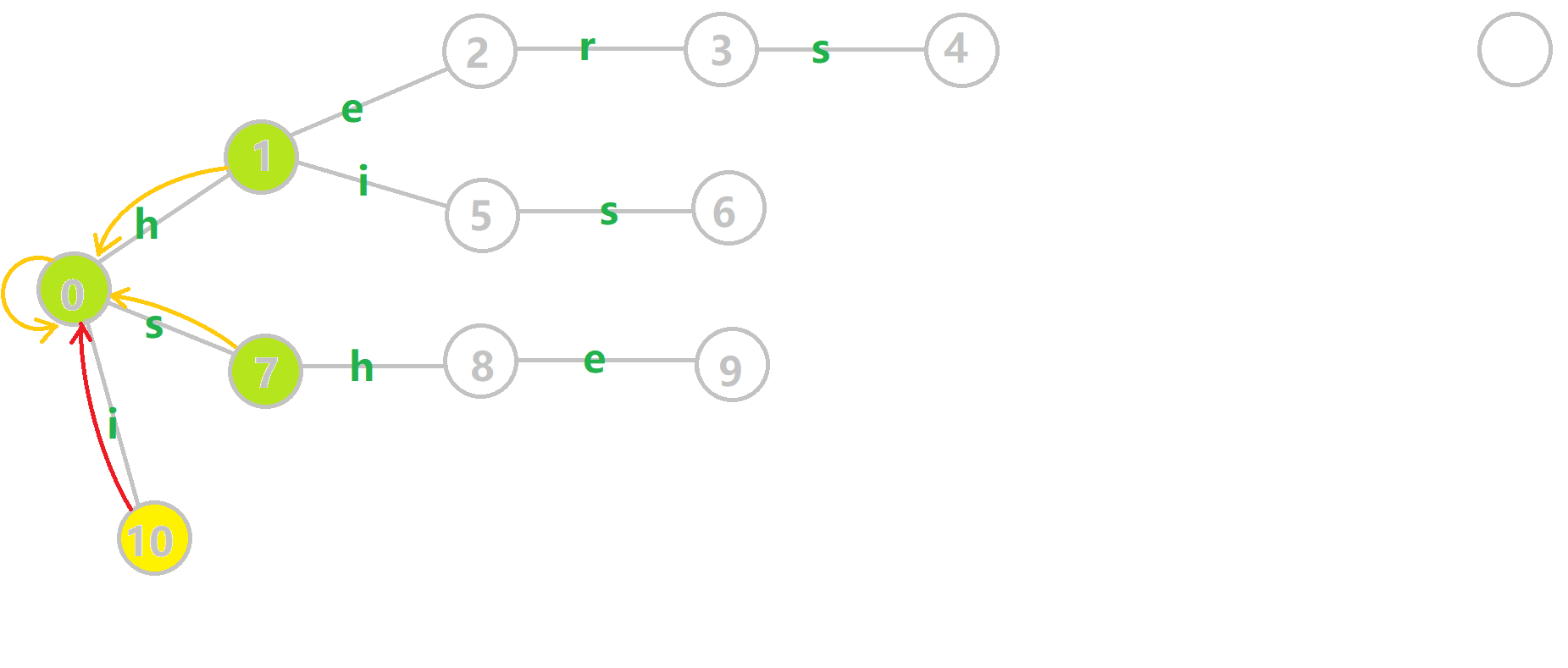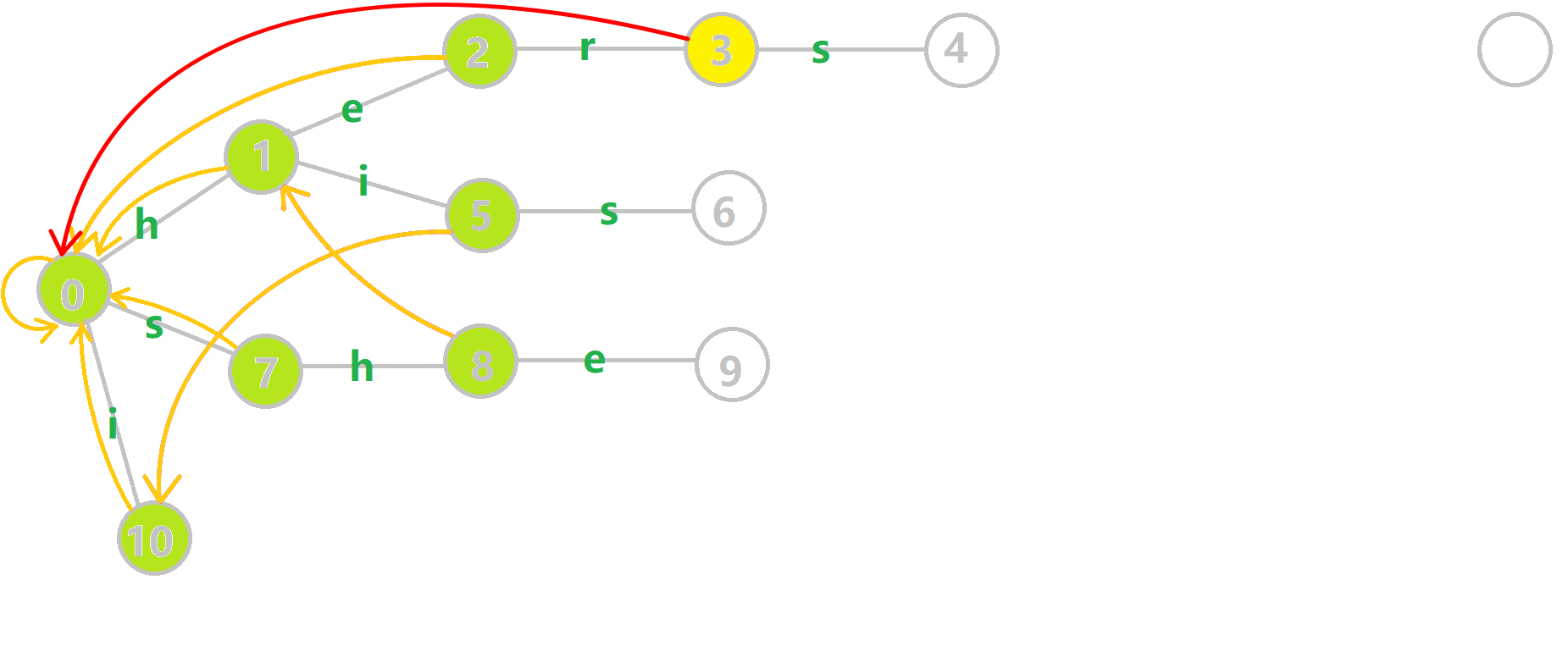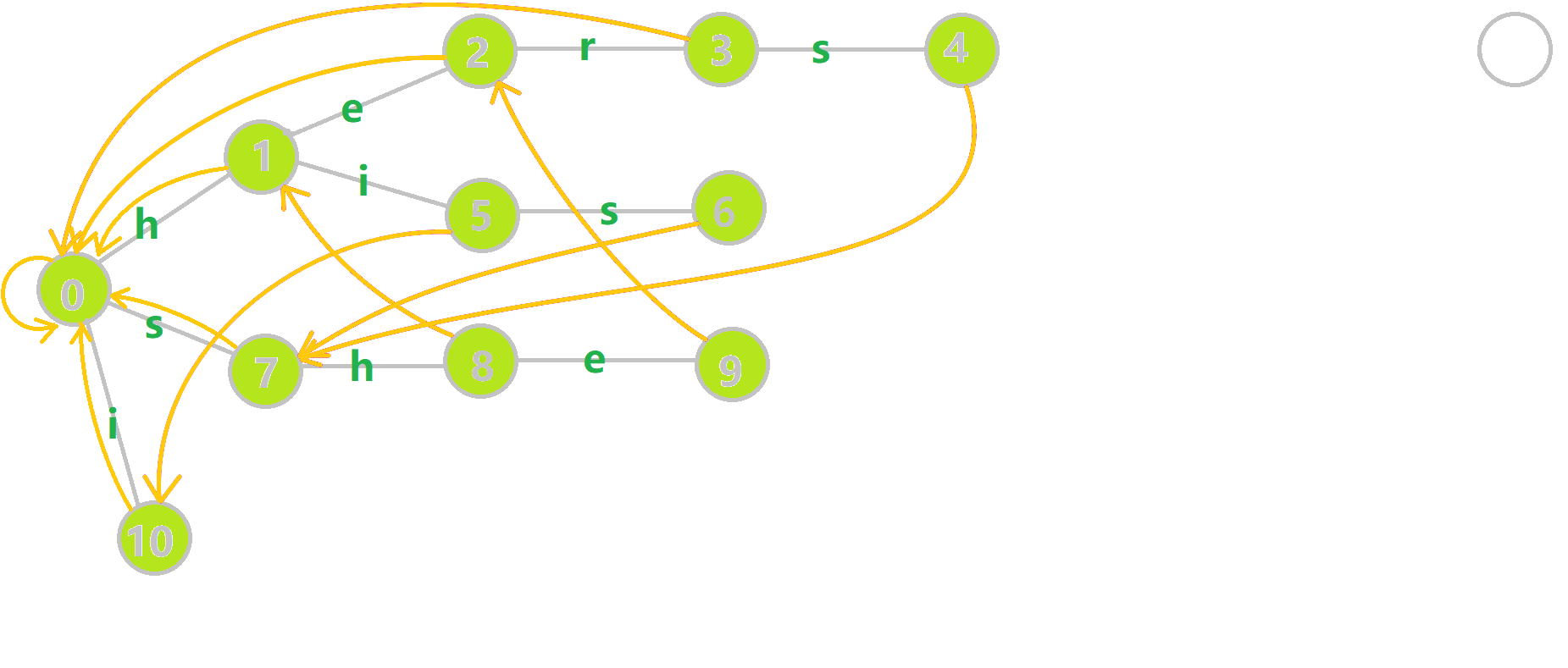
伪代码如下
q是队列, h是队头, t是队尾, tr是Trie树, c是当前位置i, u是上一层位置i - 1, j = fail[u]

因为对于Trie树来说, 节点 0 0 0是根节点, 因此插入的时候是从节点 1 1 1开始的, 因此AC自动机向前寻找fail指针的过程是j = fail[j], 而不是j = fail[j - 1]

cpp 复制代码 
   while (h <= t) {
      // 类比为i - 1
      int u = q[h++];
      for (int i = 0; i < 26; ++i) {
         int c = tr[u][i];
         // j = ne[i - 1]
         int j = fail[u];

         while (j && !tr[j][i]) j = fail[j];
         if (tr[j][i]) j = tr[j][i];
         fail[c] = j;

         q[++t] = c;
      }
   }

类比于KMP算法, AC自动机的匹配方式和构建AC自动机类似

模板代码实现

使用cnt[p]记录如果当前位置的节点编号是单词结尾 , 将该位置 + 1 +1 +1, 因此在统计单次数量的时候, 需要将指针 p p p能到达的字符串都遍历一遍, 具体的来说

假设当前指针指向了she的结尾e, p p p指针需要移动到右上方, 将he的cnt值进行累加, 因为she出现了, he也必定出现

代码实现

cpp 复制代码 
#include <bits/stdc++.h>

using namespace std;

const int N = 1e4 + 10, M = 1e6 + 10, S = 55;

int n;
int tr[N * S][26], idx, cnt[N * S];
int fail[N * S];
int q[N * S], h, t;

void insert(string &s) {
   int p = 0;
   for (int i = 0; s[i]; ++i) {
      int c = s[i] - 'a';
      if (!tr[p][c]) tr[p][c] = ++idx;
      p = tr[p][c];
   }
   cnt[p]++;
}

void build() {
   h = 0, t = -1;
   for (int i = 0; i < 26; ++i) {
      if (tr[0][i]) q[++t] = tr[0][i];
   }

   while (h <= t) {
      int u = q[h++];

      for (int i = 0; i < 26; ++i) {
         int v = tr[u][i];
         if (!v) continue;

         int j = fail[u];
         while (j && !tr[j][i]) j = fail[j];
         if (tr[j][i]) j = tr[j][i];
         fail[v] = j;
         q[++t] = v;
      }
   }
}

void solve() {
   memset(tr, 0, sizeof tr);
   memset(cnt, 0, sizeof cnt);
   memset(fail, 0, sizeof fail);
   idx = 0;

   cin >> n;
   for (int i = 0; i < n; ++i) {
      string p;
      cin >> p;
      insert(p);
   }

   build();

   string s;
   cin >> s;

   int ans = 0, j = 0;

   // 注意在计算主串的时候子节点下标是c = s[i] - 'a';
   for (int i = 0; s[i]; ++i) {
      int c = s[i] - 'a';
      while (j && !tr[j][c]) j = fail[j];
      if (tr[j][c]) j = tr[j][c];
      
      int p = j;
      while (p) {
         ans += cnt[p];
         cnt[p] = 0;
         p = fail[p];
      }
   }

   cout << ans << '\n';
}

int main() {
   ios::sync_with_stdio(false);
   cin.tie(0);

   int T;
   cin >> T;
   while (T--) solve();

   return 0;
}

Trier图

将代码的向前寻找fail指针的过程进行优化, 具体的来说

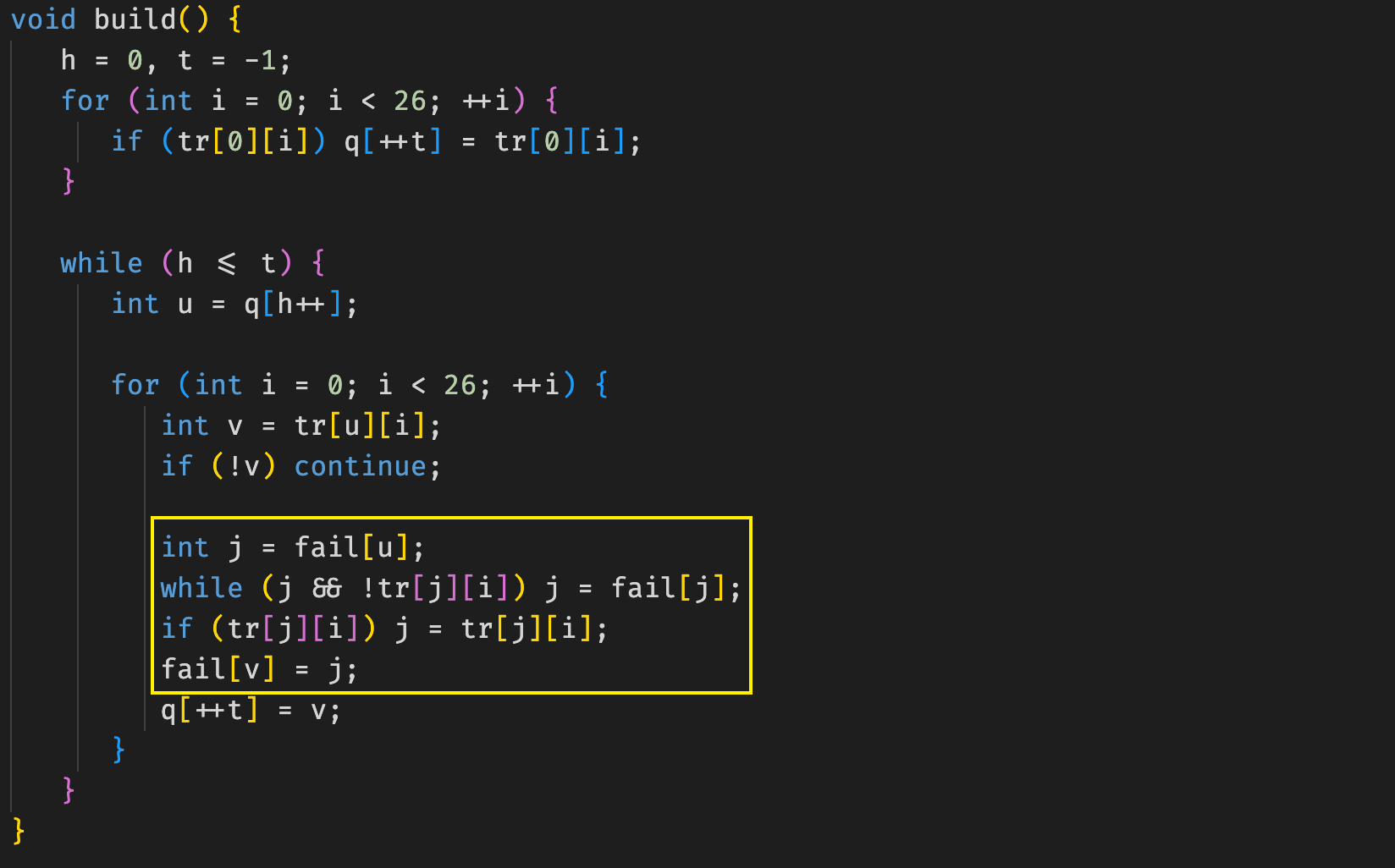
对于当前儿子 v v v

  • 如果当前儿子(是父节点的第 i i i个儿子)不存在, 那么当前儿子节点指向父节点的失败指针的第 i i i个儿子上
  • 如果当前儿子存在, 将当前儿子节点的失败指针指向父节点的失败指针的第 i i i个儿子上 , 然后将当前节点 v v v入队

因为所有的失败指针都指向某个最终节点 , 因此在查询过程中, 可以直接查询 , 具体的来说

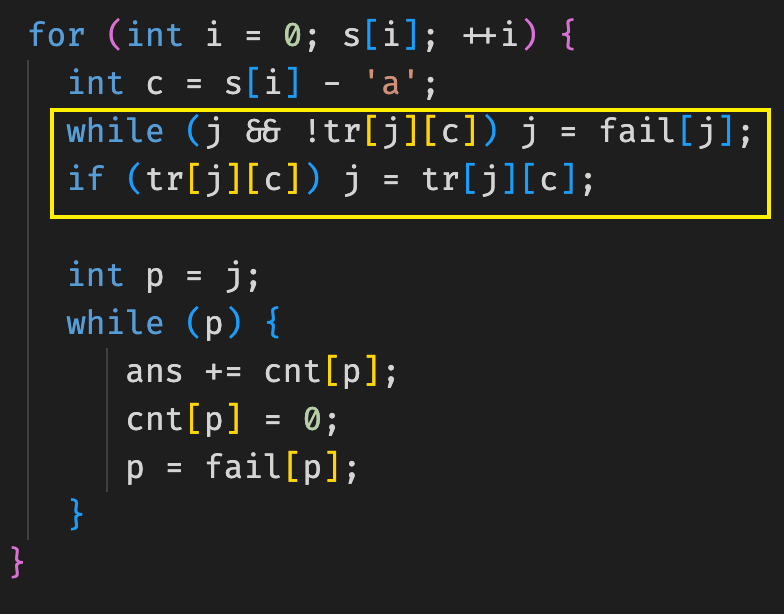
这一部分, 可以直接写成j = tr[j][c]

代码优化后

cpp 复制代码 
#include <bits/stdc++.h>

using namespace std;

const int N = 1e4 + 10, M = 1e6 + 10, S = 55;

int n;
int tr[N * S][26], idx, cnt[N * S];
int fail[N * S];
int q[N * S], h, t;

void insert(string &s) {
   int p = 0;
   for (int i = 0; s[i]; ++i) {
      int c = s[i] - 'a';
      if (!tr[p][c]) tr[p][c] = ++idx;
      p = tr[p][c];
   }
   cnt[p]++;
}

void build() {
   h = 0, t = -1;
   for (int i = 0; i < 26; ++i) {
      if (tr[0][i]) q[++t] = tr[0][i];
   }

   while (h <= t) {
      int u = q[h++];

      for (int i = 0; i < 26; ++i) {
         int v = tr[u][i];
		 
		 if (!v) tr[u][i] = tr[fail[u]][i];
		 else {
			fail[v] = tr[fail[u]][i];
			q[++t] = v;
		 }
      }
   }
}

void solve() {
   memset(tr, 0, sizeof tr);
   memset(cnt, 0, sizeof cnt);
   memset(fail, 0, sizeof fail);
   idx = 0;

   cin >> n;
   for (int i = 0; i < n; ++i) {
      string p;
      cin >> p;
      insert(p);
   }

   build();

   string s;
   cin >> s;

   int ans = 0, j = 0;
   // 注意在计算主串的时候子节点下标是c = s[i] - 'a';
   for (int i = 0; s[i]; ++i) {
      int c = s[i] - 'a';
	  j = tr[j][c];
      
      int p = j;
      while (p) {
         ans += cnt[p];
         cnt[p] = 0;
         p = fail[p];
      }
   }

   cout << ans << '\n';
}

int main() {
   ios::sync_with_stdio(false);
   cin.tie(0);

   int T;
   cin >> T;
   while (T--) solve();

   return 0;
}

例题

定义状态表示 f ( i , j ) f(i, j) f(i,j)表示考虑生成前 i i i个字符, 并且当前指向了AC自动机的第 j j j个位置 , 的所有方案中需要改变的字符数量最少的值

AC自动机朴素写法

cpp 复制代码 
#include <bits/stdc++.h>

using namespace std;

const int N = 55, M = 1010, K = 30, INF = 0x3f3f3f3f;

int T, n, m;
int tr[N * K][4], idx, cnt[N * K];
string s;
int q[N * K], h, t;
int fail[N * K];
int f[M][N * K];

int get(char c) {
	if (c == 'A') return 0;
	else if (c == 'G') return 1;
	else if (c == 'C') return 2;
	else return 3;
}

void insert(string &s) {
	int p = 0;
	for (int i = 0; s[i]; ++i) {
		int t = get(s[i]);
		if (!tr[p][t]) tr[p][t] = ++idx;
		p = tr[p][t];
	}

	cnt[p] = 1;
}

void build() {
	h = 0, t = -1;
	for (int i = 0; i < 4; ++i) {
		if (tr[0][i]) q[++t] = tr[0][i];
	}

	while (h <= t) {
		int u = q[h++];
		for (int i = 0; i < 4; ++i) {
			int v = tr[u][i];
			if (!v) continue;
			int j = fail[u];
			while (j && !tr[j][i]) j = fail[j];
			if (tr[j][i]) j = tr[j][i];
			fail[v] = j;
			q[++t] = v;
		}
	}
}

void solve() {
	memset(tr, 0, sizeof tr);
	memset(cnt, 0, sizeof cnt);
	memset(fail, 0, sizeof fail);
	memset(f, 0x3f, sizeof f);
	idx = 0;
	f[0][0] = 0;

	for (int i = 0; i < n; ++i) {
		string s;
		cin >> s;
		insert(s);
	}

	build();

	cin >> s;
	m = s.size();
	s = ' ' + s;
	
	for (int i = 0; i < m; ++i) {
		for (int j = 0; j <= idx; ++j) {
			for (int k = 0; k < 4; ++k) {
				int cost = get(s[i + 1]) != k;

				int p = j;
				while (p && !tr[p][k]) p = fail[p];
				if (tr[p][k]) p = tr[p][k];
				else p = 0;
				
				// 关键点, 检查在后缀匹配的前缀中是否有某个前缀是致病片段
				int x = p;
				bool flag = true;
				while (x) {
					if (cnt[x]) {
						flag = false;
						break;
					}
					x = fail[x];
				}
				if (flag) f[i + 1][p] = min(f[i + 1][p], f[i][j] + cost);
			}
		}
	}

	int ans = INF;
	for (int i = 0; i <= idx; ++i) ans = min(ans, f[m][i]);
	if (ans == INF) ans = -1;
	
	printf("Case %d: %d\n", ++T, ans);
}


int main() {
   ios::sync_with_stdio(false);
   cin.tie(0);

   while (cin >> n, n) solve();

   return 0;
}

Trie图 + 路径优化写法

如果当前后缀所匹配的某个前缀 有致病片段, 因为是匹配的, 当前后缀也包含那个前缀, 因此当前后缀也有致病片段, 因此可以做cnt[v] |= cnt[fail[v]]这样的优化

cpp 复制代码 
#include <bits/stdc++.h>

using namespace std;

const int N = 55, M = 1010, K = 30, INF = 0x3f3f3f3f;

int T, n, m;
int tr[N * K][4], idx, cnt[N * K];
string s;
int q[N * K], h, t;
int fail[N * K];
int f[M][N * K];

int get(char c) {
	if (c == 'A') return 0;
	else if (c == 'G') return 1;
	else if (c == 'C') return 2;
	else return 3;
}

void insert(string &s) {
	int p = 0;
	for (int i = 0; s[i]; ++i) {
		int t = get(s[i]);
		if (!tr[p][t]) tr[p][t] = ++idx;
		p = tr[p][t];
	}

	cnt[p] = 1;
}

void build() {
	h = 0, t = -1;
	for (int i = 0; i < 4; ++i) {
		if (tr[0][i]) q[++t] = tr[0][i];
	}

	while (h <= t) {
		int u = q[h++];
		for (int i = 0; i < 4; ++i) {
			int v = tr[u][i];
			if (!v) tr[u][i] = tr[fail[u]][i];
			else {
				fail[v] = tr[fail[u]][i];
				// 能够跳转到的某个前缀是否含有致病片段, 如果某个前缀有, 当前位置也有
				cnt[v] |= cnt[fail[v]];
				q[++t] = v;
			}
		}
	}
}

void solve() {
	memset(tr, 0, sizeof tr);
	memset(cnt, 0, sizeof cnt);
	memset(fail, 0, sizeof fail);
	memset(f, 0x3f, sizeof f);
	idx = 0;
	f[0][0] = 0;

	for (int i = 0; i < n; ++i) {
		string s;
		cin >> s;
		insert(s);
	}

	build();

	cin >> s;
	m = s.size();
	s = ' ' + s;
	
	for (int i = 0; i < m; ++i) {
		for (int j = 0; j <= idx; ++j) {
			for (int k = 0; k < 4; ++k) {
				int cost = get(s[i + 1]) != k;
				int p = tr[j][k];
				if (!cnt[p]) f[i + 1][p] = min(f[i + 1][p], f[i][j] + cost);
			}
		}
	}

	int ans = INF;
	for (int i = 0; i <= idx; ++i) ans = min(ans, f[m][i]);
	if (ans == INF) ans = -1;
	
	printf("Case %d: %d\n", ++T, ans);
}


int main() {
   ios::sync_with_stdio(false);
   cin.tie(0);

   while (cin >> n, n) solve();

   return 0;
}
相关推荐
带鱼吃猫5 小时前
数据结构：顺序表与基于动态顺序表的通讯录项目
数据结构·链表
报错小能手5 小时前
数据结构 AVL二叉平衡树
数据结构·算法
l1t5 小时前
利用Duckdb求解Advent of Code 2025第5题 自助餐厅
数据库·sql·mysql·算法·oracle·duckdb·advent of code
List<String> error_P5 小时前
C语言枚举类型
算法·枚举·枚举类型
liu****5 小时前
20.预处理详解
c语言·开发语言·数据结构·c++·算法
努力学算法的蒟蒻5 小时前
day26（12.6）——leetcode面试经典150
算法·leetcode·面试
代码游侠5 小时前
数据结构——哈希表
数据结构·笔记·学习·算法·哈希算法·散列表
FY_20185 小时前
Stable Baselines3中调度函数转换器get_schedule_fn 函数
开发语言·人工智能·python·算法
CoderYanger6 小时前
动态规划算法-子数组、子串系列（数组中连续的一段）：26.环绕字符串中唯一的子字符串
java·算法·leetcode·动态规划·1024程序员节
热门推荐
01GitHub 镜像站点02【超详细教程】手把手教你从微软官网免费下载Windows 10官方原版ISO镜像（2025最新版）03安娜的档案(Anna’s Archive) 镜像网站/国内最新可访问入口（持续更新）04UV安装并设置国内源05智能库存管理的需求预测模型：从业务痛点到落地代码的完整实践06BongoCat - 跨平台键盘猫动画工具07React CVE-2025-55182漏洞排查与修复指南08打造高效订单处理！ZKmall开源商城的统一履约中心架构解析09Linux下V2Ray安装配置指南10本地部署阿里最新开源的Z-Image