从0开始学算法——第八天（堆排序）

TL滕2025-12-07 13:25

写在开头的话

昨天学习完了面试高频的快速排序算法，今天让我们一起来学习一下新的排序方法------堆排序。

第一节

知识点：

（1）堆

堆

堆的定义

堆是一种树形数据结构，它通常被实现为一棵完全二叉树，其中每个节点都有零个或多个子节点。堆具有特殊的性质，即堆属性。根据堆属性，堆可以分为最大堆和最小堆两种类型。

在最大堆中，对于任意节点 x ，其父节点的值大于等于 x 的值；而在最小堆中，对于任意节点 x ，其父节点的值小于等于 x 的值。这种性质保证了堆的根节点是整个堆中的最大或最小值。

图示

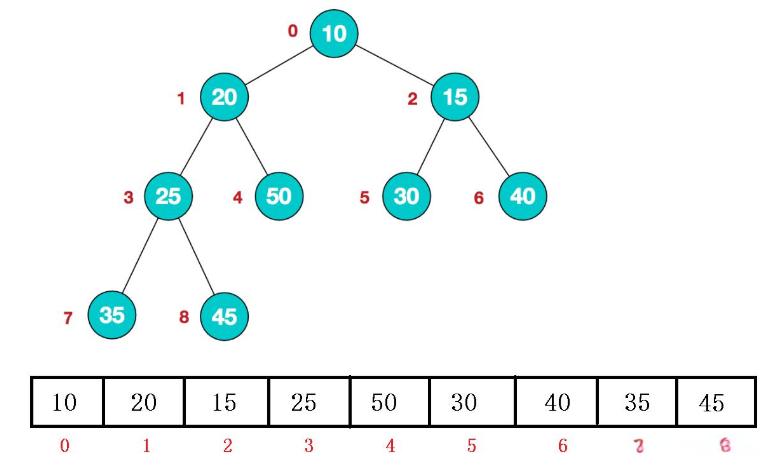
堆常被用于实现优先队列等数据结构，其中最重要的操作包括插入新元素和删除最大或最小元素。这些操作的时间复杂度为 O(log2​n) ，其中n是堆中元素的数量。这是因为堆的结构保证了树的高度是 log2​n级别的，因此插入和删除操作的时间复杂度与树的高度成正比，即 O(log2​n)。

总的来说，堆是一种高效的数据结构，可用于快速查找和操作最大或最小元素，使其在各种应用中都具有广泛的应用价值。

堆的应用场景

堆作为一种高效的数据结构，在许多应用中都有广泛的应用场景。以下是一些常见的堆应用场景：

  • 优先队列：堆常被用于实现优先队列，其中元素按照优先级顺序进行排列。优先队列通常用于任务调度、事件处理等场景，堆能够快速地插入新元素并获取最高优先级的元素。
  • 堆排序：堆排序是一种基于堆的排序算法，通过构建最大堆（或最小堆）来实现排序。堆排序具有 O(nlogn) 的时间复杂度，且不需要额外的空间，因此在某些情况下比其他排序算法更具优势。
  • 图算法 ：在图算法中，堆通常用于实现 Dijkstra 算法和 Prim 算法，用于寻找最短路径和最小生成树。堆可以帮助快速找到当前距离或权重最小的节点，从而优化算法的效率。
  • 调度器和任务管理：堆可以用于实现调度器和任务管理系统，其中任务根据优先级进行排队和执行。例如，在操作系统中，可以使用堆来管理进程的调度顺序。

堆排序的优缺点

优点

  • 高效的插入和删除操作：堆的插入和删除最大或最小元素的操作时间复杂度为O(log n)，其中n是堆中元素的数量。这使得堆非常适合于需要频繁执行这些操作的应用，例如优先队列。

  • 快速获取最大或最小元素：由于堆的特性，根节点始终是最大或最小的元素，因此获取最大或最小元素的操作非常高效，时间复杂度为 O(1)。

    • 堆的性质保证 ：堆的性质保证了根节点始终是最大或最小的元素，这使得堆非常适合于实现一些特定的算法和数据结构，例如堆排序和 Dijkstra 算法。

    • 简单的实现：相对于其他数据结构，如平衡二叉树，堆的实现通常更简单，因为它不需要维护平衡性。

缺点

  • 无法支持快速查找和更新：虽然堆可以快速获取最大或最小元素，但在堆中查找其他元素的效率较低，时间复杂度为 O(n)。此外，对于需要更新元素值的场景，堆的性质可能会导致较大的操作复杂性。

  • 不适合动态数据集合：堆通常用于静态或半静态的数据集合，即在构建堆之后，元素的数量很少发生变化。对于频繁插入和删除元素的动态数据集合，堆的性能可能不如其他数据结构，如平衡二叉搜索树。

  • 不支持有序性质：与平衡二叉搜索树相比，堆不支持对元素的有序访问。尽管堆可以按照最大或最小值的顺序访问元素，但并不保证元素之间的全局有序性。

  • 空间利用率可能较低：在某些情况下，堆可能会浪费一定的空间，特别是在使用数组表示堆时，可能会出现较多的空闲节点。

综上所述，堆是一种高效的数据结构，特别适用于需要频繁插入和删除最大或最小元素的场景，但在某些情况下，其性能和功能可能不如其他数据结构。因此，在选择数据结构时，需要根据具体的应用场景和需求来进行权衡和选择。

堆的实现步骤

初始化: 创建一个空的堆数据结构。在初始化时，可以选择使用数组或者链表来表示堆的结构。

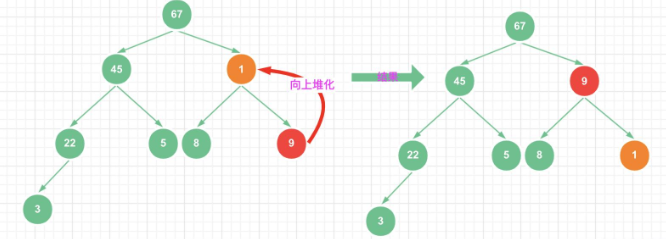
插入元素：当需要向堆中插入新元素时，首先将新元素添加到堆的末尾，然后执行一种称为"上浮"或"上调"的操作，以满足堆的性质。对于最大堆，这意味着将新元素与其父节点进行比较并交换，直到新元素的位置满足最大堆的性质；对于最小堆，则是与父节点比较并交换，直到满足最小堆的性质。

删除最大或最小元素：当需要删除堆中的最大或最小元素时，通常会删除根节点。删除后，为了保持堆的性质，将堆的最后一个元素移到根的位置，然后执行一种称为"下沉"或"下调"的操作，以满足堆的性质。对于最大堆，这意味着将根节点与其子节点中较大的节点进行比较并交换，直到根节点满足最大堆的性质；对于最小堆，则是与较小的子节点比较并交换，直到满足最小堆的性质。

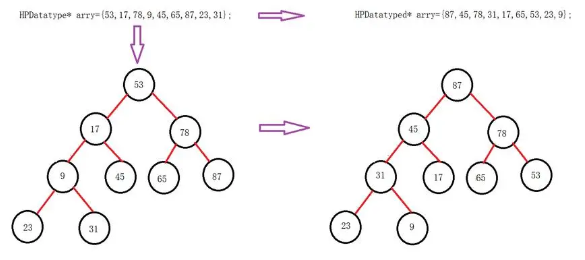
堆的构建：除了单个元素的插入和删除操作外，还可以将一个无序集合转换为堆。这个过程称为堆构建或堆化。一种常见的方法是从集合中的最后一个非叶子节点开始，依次向前进行"下沉"操作，以确保子树满足堆的性质。

其他操作：除了插入和删除操作之外，堆还支持其他一些操作，例如查找最大或最小元素、获取堆顶元素等。这些操作通常也可以在 O(log2​n) 的时间内完成，因为它们涉及到堆的高度。

堆的代码实现

C++代码实现
cpp 复制代码 
#include <iostream>
#include <vector>

using namespace std;

// 最大堆
class MaxHeap {
private:
    vector<int> heap;

    // 上浮操作
    void heapifyUp(int index) {
        // 计算父节点索引
        int parent = (index - 1) / 2;
        // 如果当前节点值大于父节点值，则交换并继续向上比较
        while (index > 0 && heap[index] > heap[parent]) {
            swap(heap[index], heap[parent]);
            index = parent;
            parent = (index - 1) / 2;
        }
    }

    // 下沉操作
    void heapifyDown(int index) {
        // 计算左右子节点索引
        int left = index * 2 + 1;
        int right = index * 2 + 2;
        int largest = index;

        // 找出左右子节点和当前节点中最大的节点
        if (left < heap.size() && heap[left] > heap[largest])
            largest = left;
        if (right < heap.size() && heap[right] > heap[largest])
            largest = right;

        // 如果最大节点不是当前节点，则交换并继续向下比较
        if (largest != index) {
            swap(heap[index], heap[largest]);
            heapifyDown(largest);
        }
    }

public:
    // 插入元素
    void insert(int val) {
        // 将新元素插入堆尾
        heap.push_back(val);
        // 执行上浮操作
        heapifyUp(heap.size() - 1);
    }

    // 删除最大元素
    void deleteMax() {
        if (heap.empty()) return;
        // 将最后一个元素移到堆顶
        heap[0] = heap.back();
        heap.pop_back();
        // 执行下沉操作
        heapifyDown(0);
    }

    // 获取最大元素
    int getMax() {
        if (heap.empty()) return -1; // or throw exception
        return heap[0];
    }
};

int main() {
    MaxHeap maxHeap;
    maxHeap.insert(5);
    maxHeap.insert(10);
    maxHeap.insert(3);
    maxHeap.insert(4);
    maxHeap.insert(5);
    maxHeap.insert(6);
    cout << "最大元素: " << maxHeap.getMax() << endl; // 输出: 10
    maxHeap.deleteMax();
    cout << "删除一个最大值后的最大值为： " << maxHeap.getMax() << endl; // 输出: 6

    return 0;
}
#include <iostream>
#include <vector>

using namespace std;

// 最大堆
class MaxHeap {
private:
    vector<int> heap;

    // 上浮操作
    void heapifyUp(int index) {
        // 计算父节点索引
        int parent = (index - 1) / 2;
        // 如果当前节点值大于父节点值，则交换并继续向上比较
        while (index > 0 && heap[index] > heap[parent]) {
            swap(heap[index], heap[parent]);
            index = parent;
            parent = (index - 1) / 2;
        }
    }

    // 下沉操作
    void heapifyDown(int index) {
        // 计算左右子节点索引
        int left = index * 2 + 1;
        int right = index * 2 + 2;
        int largest = index;

        // 找出左右子节点和当前节点中最大的节点
        if (left < heap.size() && heap[left] > heap[largest])
            largest = left;
        if (right < heap.size() && heap[right] > heap[largest])
            largest = right;

        // 如果最大节点不是当前节点，则交换并继续向下比较
        if (largest != index) {
            swap(heap[index], heap[largest]);
            heapifyDown(largest);
        }
    }

public:
    // 插入元素
    void insert(int val) {
        // 将新元素插入堆尾
        heap.push_back(val);
        // 执行上浮操作
        heapifyUp(heap.size() - 1);
    }

    // 删除最大元素
    void deleteMax() {
        if (heap.empty()) return;
        // 将最后一个元素移到堆顶
        heap[0] = heap.back();
        heap.pop_back();
        // 执行下沉操作
        heapifyDown(0);
    }

    // 获取最大元素
    int getMax() {
        if (heap.empty()) return -1; // or throw exception
        return heap[0];
    }
};

int main() {
    MaxHeap maxHeap;
    maxHeap.insert(5);
    maxHeap.insert(10);
    maxHeap.insert(3);
    maxHeap.insert(4);
    maxHeap.insert(5);
    maxHeap.insert(6);
    cout << "最大元素: " << maxHeap.getMax() << endl; // 输出: 10
    maxHeap.deleteMax();
    cout << "删除一个最大值后的最大值为： " << maxHeap.getMax() << endl; // 输出: 6

    return 0;
}
Java代码实现
java 复制代码 
import java.util.ArrayList;
import java.util.List;

// 最大堆
class MaxHeap {
    private List<Integer> heap;

    public MaxHeap() {
        heap = new ArrayList<>();
    }

    // 上浮操作
    private void heapifyUp(int index) {
        int parent = (index - 1) / 2;
        while (index > 0 && heap.get(index) > heap.get(parent)) {
            // 交换当前节点和父节点
            int temp = heap.get(index);
            heap.set(index, heap.get(parent));
            heap.set(parent, temp);
            // 更新索引
            index = parent;
            parent = (index - 1) / 2;
        }
    }

    // 下沉操作
    private void heapifyDown(int index) {
        int left = index * 2 + 1;
        int right = index * 2 + 2;
        int largest = index;

        // 找出左右子节点和当前节点中最大的节点
        if (left < heap.size() && heap.get(left) > heap.get(largest))
            largest = left;
        if (right < heap.size() && heap.get(right) > heap.get(largest))
            largest = right;

        // 如果最大节点不是当前节点，则交换并继续向下比较
        if (largest != index) {
            int temp = heap.get(index);
            heap.set(index, heap.get(largest));
            heap.set(largest, temp);
            heapifyDown(largest);
        }
    }

    // 插入元素
    public void insert(int val) {
        heap.add(val);
        heapifyUp(heap.size() - 1);
    }

    // 删除最大元素
    public void deleteMax() {
        if (heap.isEmpty()) return;
        heap.set(0, heap.get(heap.size() - 1));
        heap.remove(heap.size() - 1);
        heapifyDown(0);
    }

    // 获取最大元素
    public int getMax() {
        if (heap.isEmpty()) return -1; // or throw exception
        return heap.get(0);
    }
}

public class Main {
    public static void main(String[] args) {
        MaxHeap maxHeap = new MaxHeap();
        maxHeap.insert(5);
        maxHeap.insert(10);
        maxHeap.insert(3);
        maxHeap.insert(4);
        maxHeap.insert(5);
        maxHeap.insert(6);
        System.out.println("最大元素: " + maxHeap.getMax()); // 输出: 10
        maxHeap.deleteMax();
        System.out.println("删除一个最大值后的最大值为： " + maxHeap.getMax()); // 输出: 6
    }
}
Python代码实现
python 复制代码 
class MaxHeap:
    def __init__(self):
        self.heap = []

    # 上浮操作
    def heapify_up(self, index):
        parent = (index - 1) // 2
        while index > 0 and self.heap[index] > self.heap[parent]:
            self.heap[index], self.heap[parent] = self.heap[parent], self.heap[index]
            index = parent
            parent = (index - 1) // 2

    # 下沉操作
    def heapify_down(self, index):
        left = index * 2 + 1
        right = index * 2 + 2
        largest = index

        if left < len(self.heap) and self.heap[left] > self.heap[largest]:
            largest = left
        if right < len(self.heap) and self.heap[right] > self.heap[largest]:
            largest = right

        if largest != index:
            self.heap[index], self.heap[largest] = self.heap[largest], self.heap[index]
            self.heapify_down(largest)

    # 插入元素
    def insert(self, val):
        self.heap.append(val)
        self.heapify_up(len(self.heap) - 1)

    # 删除最大元素
    def delete_max(self):
        if not self.heap:
            return
        self.heap[0] = self.heap[-1]
        self.heap.pop()
        self.heapify_down(0)

    # 获取最大元素
    def get_max(self):
        if not self.heap:
            return -1  # or raise exception
        return self.heap[0]

# 示例用法
max_heap = MaxHeap()
max_heap.insert(5)
max_heap.insert(10)
max_heap.insert(3)
maxHeap.insert(4);
maxHeap.insert(5);
maxHeap.insert(6);
print("最大元素为：", max_heap.get_max())  # 输出: 10
max_heap.delete_max()
print("删除一个最大值后的最大值为：", max_heap.get_max())  # 输出: 6
运行结果

简单总结

在本节中，我们学习了堆的定义，实现的步骤和时间复杂度。通过学习这些堆的实现原理，我们可以对这些堆的理解进一步加深，从而更好的使用这些数据结构。堆作为一种重要的数据结构，在算法和数据结构的学习中具有不可替代的地位，它的学习不仅有助于理解基本的数据结构原理，还能够为解决实际问题提供高效的算法解决方案。

第二节

知识点：

（1）堆的操作过程（2）堆排序的性能分析

堆的操作过程

这里主要介绍各个语言中已经封装好的堆工具使用方法

C++代码

当使用 C++ 进行优先队列的操作时，STL（标准模板库）中提供了 std::priority_queue 类，它是一个模板类，用于实现优先队列的功能。优先队列是一种特殊的队列，其中的元素按照一定的优先级进行排序，优先级高的元素先被取出。

创建优先队列
cpp 复制代码 
#include <iostream>
#include <queue>

int main() {
    // 创建一个整数类型的优先队列，默认为最大堆
    std::priority_queue<int> pq;

    // 插入元素
    pq.push(3);
    pq.push(5);
    pq.push(1);

    // 输出队列中的元素
    while (!pq.empty()) {
        std::cout << pq.top() << " "; // 访问堆顶元素
        pq.pop(); // 弹出堆顶元素
    }
    std::cout << std::endl;

    return 0;
}
运行结果
自定义比较器
cpp 复制代码 
#include <iostream>
#include <queue>

struct Compare {
    bool operator() (const int& a, const int& b) {
        return a > b; // 小顶堆
    }
};

int main() {
    // 创建一个整数类型的小顶堆
    std::priority_queue<int, std::vector<int>, Compare> pq;

    // 插入元素
    pq.push(3);
    pq.push(5);
    pq.push(1);

    // 输出队列中的元素
    while (!pq.empty()) {
        std::cout << pq.top() << " "; // 访问堆顶元素
        pq.pop(); // 弹出堆顶元素
    }
    std::cout << std::endl;

    return 0;
}
运行结果
使用自定义对象

如果需要在优先队列中使用自定义对象，需要重载对象的 < 运算符或者通过自定义比较器来确定优先级。

cpp 复制代码 
#include <iostream>
#include <queue>
#include <string>

struct Person {
    std::string name;
    int age;

    Person(const std::string& n, int a) : name(n), age(a) {}

    bool operator< (const Person& other) const {
        return age < other.age;
    }
};

int main() {
    // 创建一个 Person 类型的优先队列，默认为最大堆
    std::priority_queue<Person> pq;

    // 插入元素
    pq.push(Person("Alice", 25));
    pq.push(Person("Bob", 30));
    pq.push(Person("Charlie", 20));

    // 输出队列中的元素
    while (!pq.empty()) {
        std::cout << pq.top().name << " " << pq.top().age << std::endl;
        pq.pop(); // 弹出堆顶元素
    }

    return 0;
}
运行结果

Java代码

创建优先队列
java 复制代码 
import java.util.PriorityQueue;

public class Main {
    public static void main(String[] args) {
        // 创建一个整数类型的优先队列，默认为最小堆
        PriorityQueue<Integer> pq = new PriorityQueue<>();

        // 插入元素
        pq.offer(3);
        pq.offer(5);
        pq.offer(1);

        // 输出队列中的元素
        while (!pq.isEmpty()) {
            System.out.print(pq.poll() + " "); // 弹出并返回堆顶元素
        }
        System.out.println();
    }
}
运行结果
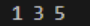
使用自定义比较器

如果需要使用自定义的比较器来确定优先级，可以通过在构造函数中指定 Comparator 来实现。

java 复制代码 
import java.util.PriorityQueue;
import java.util.Comparator;

public class Main {
    public static void main(String[] args) {
        // 创建一个整数类型的大顶堆
        PriorityQueue<Integer> pq = new PriorityQueue<>(Comparator.reverseOrder());

        // 插入元素
        pq.offer(3);
        pq.offer(5);
        pq.offer(1);

        // 输出队列中的元素
        while (!pq.isEmpty()) {
            System.out.print(pq.poll() + " "); // 弹出并返回堆顶元素
        }
        System.out.println();
    }
}
运行结果
使用自定义对象

如果需要在优先队列中使用自定义对象，需要确保对象实现了 Comparable 接口或者提供了自定义的 Comparator。

java 复制代码 
import java.util.PriorityQueue;

public class Main {
    public static void main(String[] args) {
        // 创建一个 Person 类型的优先队列，默认为最小堆
        PriorityQueue<Person> pq = new PriorityQueue<>();

        // 插入元素
        pq.offer(new Person("Alice", 25));
        pq.offer(new Person("Bob", 30));
        pq.offer(new Person("Charlie", 20));

        // 输出队列中的元素
        while (!pq.isEmpty()) {
            Person person = pq.poll();
            System.out.println(person.name + " " + person.age);
        }
    }

    static class Person implements Comparable<Person> {
        String name;
        int age;

        public Person(String name, int age) {
            this.name = name;
            this.age = age;
        }

        @Override
        public int compareTo(Person other) {
            return Integer.compare(this.age, other.age);
        }
    }
}
运行结果

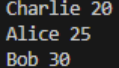
Python代码

创建优先队列
python 复制代码 
import heapq

# 创建一个整数类型的优先队列，默认为最小堆
pq = []

# 插入元素
heapq.heappush(pq, 3)
heapq.heappush(pq, 5)
heapq.heappush(pq, 1)

# 输出队列中的元素
while pq:
    print(heapq.heappop(pq), end=" ") # 弹出并返回堆顶元素
print()
运行结果
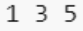
自定义对象

如果需要在优先队列中使用自定义对象，需要确保对象实现了 __lt__() 方法。

python 复制代码 
import heapq

class Person:
    def __init__(self, name, age):
        self.name = name
        self.age = age

    def __lt__(self, other):
        return self.age < other.age

# 创建一个 Person 类型的优先队列，默认为最小堆
pq = []

# 插入元素
heapq.heappush(pq, Person("Alice", 25))
heapq.heappush(pq, Person("Bob", 30))
heapq.heappush(pq, Person("Charlie", 20))

# 输出队列中的元素
while pq:
    person = heapq.heappop(pq)
    print(person.name, person.age)
运行结果

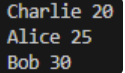
堆排序的性能分析

总的来说，堆排序是一种原地、不稳定、时间复杂度为 O(nlogn) 的排序算法。

时间复杂度

  • 建堆时间复杂度 ：构建堆的时间复杂度为 O(n) ，其中 nn 是待排序数组的长度。因为堆是一个完全二叉树，从最后一个非叶子节点开始向上调整堆的过程只需要 O(n) 的时间复杂度。
  • 排序时间复杂度 ：取出堆顶元素并调整堆的过程需要 O(logn) 的时间复杂度，而总共有 n 次这样的操作，因此排序的时间复杂度为 O(nlogn)。

空间复杂度

堆排序是一种原地排序算法，不需要额外的空间，因此其空间复杂度为 O(1) 。

稳定性

堆排序是一种不稳定的排序算法。因为在构建堆和调整堆的过程中，可能会改变相同元素的相对顺序，从而导致排序后相同元素的顺序发生变化。

简单总结

本节主要实现了堆排序的插入和删除元素操作，并且分析了堆排序为什么是一种原地、不稳定、时间复杂度为 O(nlogn) 的排序算法。

相关推荐
Ayanami_Reii4 小时前
进阶数据结构-AC自动机
数据结构·算法·动态规划·字符串·ac自动机
崇山峻岭之间4 小时前
C++ Prime Plus 学习笔记030
c++·笔记·学习
报错小能手5 小时前
数据结构 AVL二叉平衡树
数据结构·算法
l1t5 小时前
利用Duckdb求解Advent of Code 2025第5题 自助餐厅
数据库·sql·mysql·算法·oracle·duckdb·advent of code
List<String> error_P5 小时前
C语言枚举类型
算法·枚举·枚举类型
liu****5 小时前
20.预处理详解
c语言·开发语言·数据结构·c++·算法
努力学算法的蒟蒻5 小时前
day26（12.6）——leetcode面试经典150
算法·leetcode·面试
代码游侠5 小时前
数据结构——哈希表
数据结构·笔记·学习·算法·哈希算法·散列表
FY_20185 小时前
Stable Baselines3中调度函数转换器get_schedule_fn 函数
开发语言·人工智能·python·算法
热门推荐
01GitHub 镜像站点02【超详细教程】手把手教你从微软官网免费下载Windows 10官方原版ISO镜像（2025最新版）03安娜的档案(Anna’s Archive) 镜像网站/国内最新可访问入口（持续更新）04UV安装并设置国内源05智能库存管理的需求预测模型：从业务痛点到落地代码的完整实践06BongoCat - 跨平台键盘猫动画工具07React CVE-2025-55182漏洞排查与修复指南08打造高效订单处理！ZKmall开源商城的统一履约中心架构解析09Linux下V2Ray安装配置指南10本地部署阿里最新开源的Z-Image