【微实验】大规模网络的社区检测Clauset–Newman–Moore聚类算法（附完整MATLAB代码）

🌐 序章：网络迷宫中的隐秘秩序

"万物皆有群，网络藏章法 ------ 模块化是解码复杂系统关联本质的密钥。"

打开学术合作数据库，数百位学者的合作关系交织成一张密网；滑动关键词共现图谱，成千上万个术语在语义空间中彼此牵连。这些看似杂乱无章的网络背后，是否存在着隐秘的 "社区"？网络节点是否会按某种规则形成紧密相连的 "模块"？------CNM（Clauset--Newman--Moore）算法，是一位 "网络考古学家"，用高效的贪心策略，从海量连接中挖掘出复杂网络的模块化秩序。

🤔 困境：海量连接中的 "社区迷雾"

生活中的类比：寻找社交圈的核心

想象一个有上千人的大型公司，员工间的沟通构成一张复杂的社交网络。如何快速找出哪些人形成了紧密协作的团队？若逐个排查每两个人的关系，就像在茫茫人海中逐一询问 "你和他是否熟悉"，不仅效率低下，还容易遗漏隐藏的协作群体。

技术核心痛点：大规模网络的社区检测难题

现实中的网络（如学术合作网、语义共现网）往往具备 "大规模" 和 "无向加权" 特性：节点数动辄数千甚至上万，边的数量呈指数级增长。传统的 GN算法虽能检测社区，但时间复杂度高达\(O(n^3)\)，面对大规模网络时如同 "蜗牛爬金字塔"；而简单的聚类方法又无法精准捕捉网络的 "模块化" 本质 ------ 即社区内部连接紧密、社区间连接稀疏的核心特征。

CNM 算法的诞生，正是为了解决 "大规模网络下高效且精准的社区划分" 这一核心痛点，其核心思路是：用 "模块化 Q 值" 量化社区划分质量，通过贪心合并策略，在保证精度的同时大幅提升计算效率。

📚 数学之美：从公式到模块化本质

核心定义：模块化 Q 值的物理意义

模块化 Q 值是衡量社区划分优劣的核心指标，其本质是 "社区内部实际边数与随机网络中期望边数的差值占比"。公式定义如下：\(Q = \frac{1}{2m} \sum_{i,j} \left( A_{ij} - \frac{k_i k_j}{2m} \right) \delta(c_i, c_j)\)

通俗类比：Q 值就像 "社区凝聚力评分"------ 内部连接越密集、外部连接越稀疏，评分越高（取值范围 [-1/2, 1]，越接近 1 划分效果越好）。
关键参数解读：
- \(A_{ij}\)：节点 i 和 j 间的边权（无连接时为 0）；
- \(k_i = \sum_j A_{ij}\)：节点 i 的总度数（所有连接的边权和）；
- \(m = \frac{1}{2} \sum_{i,j} A_{ij}\)：网络总边权的一半（标准化系数）；
- \(\delta(c_i, c_j)\)：指示函数（节点 i 和 j 属于同一社区时为 1，否则为 0）。

贪心合并的数学逻辑：增量式优化

CNM 算法没有盲目枚举所有可能的社区划分，而是通过 "合并一次、优化一次" 的贪心策略，逐步逼近最优解。核心是计算社区合并的模块化增量\(\Delta Q\)：\(\Delta Q = \frac{1}{2m} \left( 2e_{uv} - \frac{k_u k_v}{m} \right)\)

公式意义：量化 "将社区 u 和 v 合并后，Q 值的变化量"------\(\Delta Q > 0\)说明合并能提升划分质量。
通俗解读：
- \(e_{uv}\)：社区 u 和 v 间的边权和（相当于两个 "街区" 之间的通道总数）；
- \(k_u\)、\(k_v\)：社区 u、v 的总度数（相当于每个 "街区" 的总出入口数）；
- 整个公式本质是 "实际跨社区边数与期望跨社区边数的差值"，正值意味着合并后社区结构更清晰。

算法流程的数学严谨性

初始化：每个节点单独作为一个社区，计算初始 Q 值\(Q_0\)；
增量计算：对所有相邻社区对，计算合并后的\(\Delta Q\)；
贪心合并：选择\(\Delta Q\)最大的社区对合并，更新社区信息；
终止条件：重复步骤 2-3，直到所有节点合并为一个社区，取整个过程中 Q 值最大的划分结果（避免过度合并导致社区消失）。

⚙️ 实践落地：MATLAB 实现 CNM 算法

以下是完整的 MATLAB 脚本，支持大规模无向加权网络的社区检测，包含数据生成、算法实现、多参数对比和可视化展示，所有模块均有详细注释：

Matlab 复制代码

% =========================================================================
% 代码功能说明：CNM（Clauset--Newman--Moore）算法实现大规模无向加权网络社区检测
% 支持功能：1. 生成模拟网络数据（含已知社区标签，用于验证算法效果）
%          2. 核心CNM算法实现（贪心合并+模块化Q值计算）
%          3. 多参数对比（不同网络密度下的算法性能）
%          4. 全流程可视化（原始网络、社区划分结果、Q值变化曲线、模块结构热力图）
% 依赖说明：仅使用MATLAB自带函数，无需额外工具箱
% 兼容性：MATLAB R2016b及以上版本
% =========================================================================

clear; clc; close all;

%% 1. 生成模拟无向加权网络（含真实社区标签，用于验证）
fprintf('正在生成模拟网络数据...\n');
% 网络参数设置
n_nodes = 200;              % 总节点数（大规模网络可调整为1000+）
n_communities = 4;          % 真实社区数量
community_sizes = [50, 50, 50, 50];  % 每个社区的节点数（均匀分布，可修改为非均匀对比局限）
density_intra = 0.6;        % 社区内部连接密度（内部紧密）
density_inter = 0.05;       % 社区之间连接密度（外部稀疏）
weight_range = [1, 5];      % 边权取值范围（1-5的整数）

% 生成节点社区标签（1~n_communities）
true_labels = [];
for i = 1:n_communities
    true_labels = [true_labels, ones(1, community_sizes(i)) * i];
end

% 生成无向加权邻接矩阵A（A(i,j)=A(j,i)，对角线为0）
A = zeros(n_nodes);
for i = 1:n_nodes
    for j = i+1:n_nodes  % 上三角矩阵赋值，避免重复
        if true_labels(i) == true_labels(j)
            % 社区内部：按密度生成边，边权随机
            if rand() < density_intra
                A(i,j) = randi(weight_range);
                A(j,i) = A(i,j);  % 无向网络对称性
            end
        else
            % 社区之间：按低密度生成边，边权随机
            if rand() < density_inter
                A(i,j) = randi(weight_range);
                A(j,i) = A(i,j);
            end
        end
    end
end

% 计算网络基础参数
k = sum(A, 2);              % 每个节点的总度数（列求和，得到n×1向量）
m = sum(sum(A)) / 2;        % 网络总边权的一半（无向网络避免重复计算）

% 可视化1：原始网络（节点颜色表示真实社区）
figure('Position', [100, 100, 800, 600]);
subplot(2,2,1);
% 使用兼容性更好的网络可视化方法
G = graph(A);
if exist('layout', 'file') == 2
    % 新版本MATLAB使用layout
    layout(G, 'force', 'Iterations', 500);
else
    % 旧版本MATLAB使用手动布局
    L = layout_force(G, 500);
end

% 创建节点颜色映射
cmap = lines(n_communities);
node_colors = zeros(n_nodes, 3);
for i = 1:n_nodes
    node_colors(i,:) = cmap(true_labels(i), :);
end

% 绘制网络图（兼容旧版本）
try
    % 尝试新版本的plot方法
    h1 = plot(G, 'NodeColor', node_colors, 'MarkerSize', 8, 'LineWidth', 0.5);
catch
    % 旧版本兼容方法
    if exist('L', 'var')
        h1 = plot(G, 'XData', L(:,1), 'YData', L(:,2), ...
            'NodeColor', node_colors, 'MarkerSize', 8, 'LineWidth', 0.5);
    else
        h1 = plot(G, 'NodeColor', node_colors, 'MarkerSize', 8, 'LineWidth', 0.5);
    end
end

title('原始网络（颜色=真实社区）', 'FontSize', 12, 'FontWeight', 'bold');
colormap(cmap);
colorbar('Ticks', 1:n_communities, 'TickLabels', arrayfun(@(x) sprintf('社区%d', x), 1:n_communities, 'UniformOutput', false));
fprintf('网络生成完成：%d个节点，%d条边，%d个真实社区\n', n_nodes, sum(sum(A>0))/2, n_communities);

%% 2. CNM算法核心实现
fprintf('\n正在运行CNM算法...\n');
% 初始化：每个节点为一个独立社区
current_communities = 1:n_nodes;  % 社区标签（初始为节点索引）
n_current = n_nodes;              % 当前社区数量
Q_history = [];                   % 记录每次合并后的Q值
best_Q = -inf;                    % 最优Q值
best_partition = current_communities;  % 最优社区划分

% 计算初始模块化Q值（所有节点各自为社区，Q0通常接近0）
initial_Q = calculate_modularity(A, current_communities, m);
Q_history = [Q_history, initial_Q];
if initial_Q > best_Q
    best_Q = initial_Q;
    best_partition = current_communities;
end

% 记录合并历史用于调试
merge_history = [];

% 迭代合并社区
iteration = 0;
while n_current > 1
    iteration = iteration + 1;
    
    % 步骤1：获取所有当前社区的唯一标签
    unique_comms = unique(current_communities);
    n_unique = length(unique_comms);
    
    % 步骤2：计算所有相邻社区对的ΔQ
    max_delta_Q = -inf;
    merge_pair = [0, 0];  % 记录要合并的社区对（u, v）
    
    % 构建社区节点映射
    comm_nodes = cell(1, n_unique);
    comm_degrees = zeros(1, n_unique);
    
    for u_idx = 1:n_unique
        u = unique_comms(u_idx);
        nodes_u = find(current_communities == u);
        comm_nodes{u_idx} = nodes_u;
        comm_degrees(u_idx) = sum(k(nodes_u));
    end
    
    for u_idx = 1:n_unique-1
        u = unique_comms(u_idx);
        nodes_u = comm_nodes{u_idx};
        k_u = comm_degrees(u_idx);
        
        for v_idx = u_idx+1:n_unique
            v = unique_comms(v_idx);
            nodes_v = comm_nodes{v_idx};
            
            % 计算社区u和v之间的边权和e_uv
            e_uv = sum(sum(A(nodes_u, nodes_v)));
            
            % 社区v的总度数k_v
            k_v = comm_degrees(v_idx);
            
            % 计算ΔQ（核心公式）
            if m > 0  % 避免除以零
                delta_Q = (2 * e_uv - (k_u * k_v) / m) / (2 * m);
            else
                delta_Q = 0;
            end
            
            % 更新最大ΔQ和对应的合并对
            if delta_Q > max_delta_Q
                max_delta_Q = delta_Q;
                merge_pair = [u, v];
                merge_pair_indices = [u_idx, v_idx];
            end
        end
    end
    
    % 步骤3：合并ΔQ最大的社区对
    if merge_pair(1) > 0 && merge_pair(2) > 0
        current_communities(current_communities == merge_pair(2)) = merge_pair(1);
        merge_history = [merge_history; merge_pair];
        n_current = n_current - 1;
        
        % 步骤4：计算当前Q值，更新最优划分
        current_Q = calculate_modularity(A, current_communities, m);
        Q_history = [Q_history, current_Q];
        
        if current_Q > best_Q
            best_Q = current_Q;
            best_partition = current_communities;
        end
        
        % 进度提示
        if mod(n_current, 20) == 0
            fprintf('当前社区数：%d，最优Q值：%.4f\n', n_current, best_Q);
        end
    else
        % 如果没有可以合并的社区对，提前结束
        break;
    end
end

% 结果整理：将最优划分标签重新编码为1~n_best_communities
[~, ~, best_labels] = unique(best_partition);
n_best_communities = max(best_labels);
fprintf('\nCNM算法运行完成！迭代次数：%d，最优社区数：%d，最优Q值：%.4f\n', iteration, n_best_communities, best_Q);

%% 3. 多参数对比：不同网络密度下的算法性能
fprintf('\n正在进行多参数对比实验...\n');
density_intra_list = [0.4, 0.6, 0.8];  % 不同内部连接密度
density_inter = 0.05;                  % 固定外部连接密度
compare_results = struct('density_intra', [], 'n_communities', [], 'Q_value', []);

for idx = 1:length(density_intra_list)
    % 生成不同密度的网络
    A_compare = zeros(n_nodes);
    for i = 1:n_nodes
        for j = i+1:n_nodes
            if true_labels(i) == true_labels(j)
                if rand() < density_intra_list(idx)
                    A_compare(i,j) = randi(weight_range);
                    A_compare(j,i) = A_compare(i,j);
                end
            else
                if rand() < density_inter
                    A_compare(i,j) = randi(weight_range);
                    A_compare(j,i) = A_compare(i,j);
                end
            end
        end
    end
    
    % 运行CNM算法
    [q_compare, labels_compare] = run_cnm_algorithm(A_compare, n_nodes);
    n_compare = max(labels_compare);
    
    % 保存结果
    compare_results(idx).density_intra = density_intra_list(idx);
    compare_results(idx).n_communities = n_compare;
    compare_results(idx).Q_value = q_compare;
    
    fprintf('内部密度=%.1f：检测社区数=%d，Q值=%.4f\n', density_intra_list(idx), n_compare, q_compare);
end

%% 4. 全流程可视化展示
% 可视化2：CNM算法检测结果（节点颜色表示检测社区）
subplot(2,2,2);
G_best = graph(A);

% 创建检测结果的颜色映射
cmap_best = lines(n_best_communities);
node_colors_best = zeros(n_nodes, 3);
for i = 1:n_nodes
    node_colors_best(i,:) = cmap_best(best_labels(i), :);
end

% 绘制检测结果图
try
    % 尝试保持与原始图相同的布局
    h2 = plot(G_best, 'NodeColor', node_colors_best, 'MarkerSize', 8, 'LineWidth', 0.5);
catch
    % 如果失败，使用默认布局
    h2 = plot(G_best, 'NodeColor', node_colors_best, 'MarkerSize', 8, 'LineWidth', 0.5);
end

title(sprintf('CNM检测结果（Q=%.4f，社区数=%d）', best_Q, n_best_communities), 'FontSize', 12, 'FontWeight', 'bold');
colormap(cmap_best);
colorbar('Ticks', 1:n_best_communities, 'TickLabels', arrayfun(@(x) sprintf('簇%d', x), 1:n_best_communities, 'UniformOutput', false));

% 可视化3：Q值变化曲线（展示合并过程中的优化趋势）
subplot(2,2,3);
plot(0:length(Q_history)-1, Q_history, 'LineWidth', 2, 'Color', [0.2, 0.6, 0.8]);
xlabel('合并次数', 'FontSize', 10);
ylabel('模块化Q值', 'FontSize', 10);
title('Q值变化曲线（峰值为最优解）', 'FontSize', 12, 'FontWeight', 'bold');
grid on;

% 标记最优Q值位置
[~, best_idx] = max(Q_history);
hold on;
scatter(best_idx-1, best_Q, 60, 'r', 'filled');
text(best_idx-1, best_Q+0.01, sprintf('最优Q=%.4f', best_Q), 'FontSize', 9, 'Color', 'r', 'BackgroundColor', 'white');
hold off;

% 添加参考线
xline(best_idx-1, '--', 'Color', [0.8, 0.2, 0.2], 'LineWidth', 1, 'Alpha', 0.5);
yline(best_Q, '--', 'Color', [0.8, 0.2, 0.2], 'LineWidth', 1, 'Alpha', 0.5);

% 可视化4：多参数对比柱状图（不同密度下的Q值）
subplot(2,2,4);
density_labels = cellfun(@(x) sprintf('%.1f', x), num2cell(density_intra_list), 'UniformOutput', false);
q_values = [compare_results.Q_value];
bar(q_values, 'FaceColor', [0.6, 0.3, 0.8], 'EdgeColor', 'black');
xlabel('社区内部连接密度', 'FontSize', 10);
ylabel('最优模块化Q值', 'FontSize', 10);
title('不同网络密度下的算法性能', 'FontSize', 12, 'FontWeight', 'bold');
set(gca, 'XTick', 1:length(density_labels), 'XTickLabel', density_labels);
grid on;

% 在柱状图上添加数值标签
for i = 1:length(q_values)
    text(i, q_values(i)+0.005, sprintf('%.4f', q_values(i)), 'FontSize', 9, 'HorizontalAlignment', 'center');
end

% 添加理论最大值参考线
hold on;
plot([0, length(q_values)+1], [1, 1], 'r--', 'LineWidth', 1);
text(length(q_values)+0.1, 0.98, '理论最大值=1', 'FontSize', 9, 'Color', 'r');
hold off;

% 额外可视化：社区结构热力图（展示模块内/间连接密度）
figure('Position', [200, 200, 700, 500]);
% 按最优社区标签排序邻接矩阵
[sorted_labels, sort_idx] = sort(best_labels);
A_sorted = A(sort_idx, sort_idx);

% 绘制热力图
imagesc(A_sorted, [0, max(weight_range)]);
colormap(jet);
colorbar;
title('社区结构热力图（颜色深浅=边权大小）', 'FontSize', 14, 'FontWeight', 'bold');
xlabel('节点（按社区排序）', 'FontSize', 12);
ylabel('节点（按社区排序）', 'FontSize', 12);

% 绘制社区分隔线
community_counts = histcounts(sorted_labels);
community_edges = cumsum(community_counts);
for i = 1:n_best_communities-1
    line([community_edges(i)+0.5, community_edges(i)+0.5], [0.5, n_nodes+0.5], ...
        'Color', 'white', 'LineWidth', 2);
    line([0.5, n_nodes+0.5], [community_edges(i)+0.5, community_edges(i)+0.5], ...
        'Color', 'white', 'LineWidth', 2);
end

% 添加社区标签
for i = 1:n_best_communities
    if i == 1
        x_pos = community_counts(1)/2;
        y_pos = community_counts(1)/2;
    else
        x_pos = community_edges(i-1) + community_counts(i)/2;
        y_pos = community_edges(i-1) + community_counts(i)/2;
    end
    text(x_pos, y_pos, sprintf('社区%d', i), 'FontSize', 11, 'FontWeight', 'bold', ...
        'HorizontalAlignment', 'center', 'Color', 'white');
end

%% 5. 精度评估：与真实社区的对比
fprintf('\n==================== 精度评估 ====================\n');
% 计算调整Rand指数（ARI）
ari = calculate_adjusted_rand_index(true_labels', best_labels);
fprintf('调整Rand指数(ARI): %.4f\n', ari);

% 计算归一化互信息（NMI）
nmi = calculate_normalized_mutual_info(true_labels', best_labels);
fprintf('归一化互信息(NMI): %.4f\n', nmi);

% 计算模块化密度
modularity_density = calculate_modularity_density(A, best_labels);
fprintf('模块化密度: %.4f\n', modularity_density);

% 社区大小统计
fprintf('\n真实社区大小分布: ');
fprintf('%d ', community_sizes);
fprintf('\n检测社区大小分布: ');
comm_sizes_detected = histcounts(best_labels, 1:(n_best_communities+1));
fprintf('%d ', comm_sizes_detected);
fprintf('\n');

%% 6. 结果解读与分析
fprintf('\n==================== 结果解读 ====================\n');
fprintf('1. 算法有效性：最优Q值=%.4f（接近1表示划分效果优秀），检测到%d个社区\n', best_Q, n_best_communities);
fprintf('   调整Rand指数=%.4f（1为完美匹配，0为随机匹配）\n', ari);
fprintf('   归一化互信息=%.4f（1为完全一致，0为无关）\n', nmi);

fprintf('2. 网络密度影响：\n');
for idx = 1:length(density_intra_list)
    fprintf('   密度=%.1f时，Q值=%.4f\n', density_intra_list(idx), compare_results(idx).Q_value);
end
fprintf('   结论：内部连接密度越大，社区结构越清晰，算法效果越好\n');

fprintf('3. 算法优势：\n');
fprintf('   • 时间复杂度：O(n²)，适合处理%d个节点的大规模网络\n', n_nodes);
fprintf('   • 内存效率：无需存储全距离矩阵，节省内存空间\n');
fprintf('   • 结果稳定：贪心策略保证每次合并都是局部最优\n');

fprintf('4. 局限说明：\n');
fprintf('   • 对社区大小差异大的网络适应性较弱\n');
fprintf('   • 贪心策略可能陷入局部最优\n');
fprintf('   • 需要设置合适的终止条件\n');

fprintf('5. 改进方向：\n');
fprintf('   • 引入多分辨率参数调节\n');
fprintf('   • 结合其他算法（如Louvain）的初始化策略\n');
fprintf('   • 添加并行计算加速大规模网络处理\n');

fprintf('==================================================\n');

%% 运行说明
% 1. 无需额外依赖，直接复制脚本到MATLAB运行即可；
% 2. 可修改参数：n_nodes（节点数）、n_communities（真实社区数）、density_intra（内部密度）等；
% 3. 输出结果：2个可视化窗口（网络对比图+热力图），控制台输出算法进度和性能分析；
% 4. 真实数据适配：将A矩阵替换为真实网络的邻接矩阵（无向加权），即可直接运行检测。

%% ========================================================================
% 辅助函数定义（必须放在脚本末尾）
% ========================================================================

function Q = calculate_modularity(A, communities, m)
    % 计算模块化Q值（优化版）
    n = size(A, 1);
    if n == 0 || m == 0
        Q = 0;
        return;
    end
    
    unique_comms = unique(communities);
    n_comms = length(unique_comms);
    
    % 预计算社区度数和社区内边权和
    comm_degrees = zeros(1, n_comms);
    comm_internal_edges = zeros(1, n_comms);
    
    % 创建社区到索引的映射
    comm_map = containers.Map(unique_comms, 1:n_comms);
    
    % 第一次遍历：计算社区度数和内部边权
    for i = 1:n
        comm_i = communities(i);
        idx_i = comm_map(comm_i);
        k_i = sum(A(i, :));
        comm_degrees(idx_i) = comm_degrees(idx_i) + k_i;
        
        for j = i+1:n
            if communities(j) == comm_i
                comm_internal_edges(idx_i) = comm_internal_edges(idx_i) + A(i, j);
            end
        end
    end
    
    % 计算Q值
    Q = 0;
    for i = 1:n_comms
        Q = Q + (comm_internal_edges(i) / m) - (comm_degrees(i) / (2 * m))^2;
    end
end

function [best_Q, best_labels] = run_cnm_algorithm(A, n_nodes)
    % 独立运行CNM算法（用于多参数对比）
    k = sum(A, 2);
    m = sum(sum(A)) / 2;
    
    if m == 0
        best_Q = 0;
        best_labels = ones(n_nodes, 1);
        return;
    end
    
    current_communities = 1:n_nodes;
    best_Q = -inf;
    best_partition = current_communities;
    
    % 计算初始Q值
    initial_Q = calculate_modularity(A, current_communities, m);
    if initial_Q > best_Q
        best_Q = initial_Q;
        best_partition = current_communities;
    end
    
    % 贪心合并
    n_current = n_nodes;
    while n_current > 1
        unique_comms = unique(current_communities);
        n_unique = length(unique_comms);
        
        if n_unique <= 1
            break;
        end
        
        max_delta_Q = -inf;
        merge_pair = [0, 0];
        
        % 预计算社区信息
        comm_nodes = cell(1, n_unique);
        comm_degrees = zeros(1, n_unique);
        
        for i = 1:n_unique
            comm = unique_comms(i);
            nodes = find(current_communities == comm);
            comm_nodes{i} = nodes;
            comm_degrees(i) = sum(k(nodes));
        end
        
        % 查找最优合并对
        for i = 1:n_unique-1
            nodes_i = comm_nodes{i};
            k_i = comm_degrees(i);
            
            for j = i+1:n_unique
                nodes_j = comm_nodes{j};
                
                % 计算社区间边权和
                e_ij = sum(sum(A(nodes_i, nodes_j)));
                k_j = comm_degrees(j);
                
                % 计算ΔQ
                delta_Q = (2 * e_ij - (k_i * k_j) / m) / (2 * m);
                
                if delta_Q > max_delta_Q
                    max_delta_Q = delta_Q;
                    merge_pair = [unique_comms(i), unique_comms(j)];
                end
            end
        end
        
        % 合并社区
        if max_delta_Q > -inf && merge_pair(1) > 0 && merge_pair(2) > 0
            current_communities(current_communities == merge_pair(2)) = merge_pair(1);
            n_current = n_current - 1;
            
            % 更新最优划分
            current_Q = calculate_modularity(A, current_communities, m);
            if current_Q > best_Q
                best_Q = current_Q;
                best_partition = current_communities;
            end
        else
            break;
        end
    end
    
    % 重新编码标签
    [~, ~, best_labels] = unique(best_partition);
end

function ari = calculate_adjusted_rand_index(true_labels, pred_labels)
    % 计算调整Rand指数（ARI）
    n = length(true_labels);
    
    % 创建混淆矩阵
    true_unique = unique(true_labels);
    pred_unique = unique(pred_labels);
    n_true = length(true_unique);
    n_pred = length(pred_unique);
    
    confusion_matrix = zeros(n_true, n_pred);
    for i = 1:n_true
        for j = 1:n_pred
            confusion_matrix(i,j) = sum((true_labels == true_unique(i)) & (pred_labels == pred_unique(j)));
        end
    end
    
    % 计算各项指标
    a = 0;  % 同簇同预测的对数
    b = 0;  % 不同簇不同预测的对数
    
    % 计算行和列的和
    row_sum = sum(confusion_matrix, 2);
    col_sum = sum(confusion_matrix, 1);
    
    % 计算a
    for i = 1:n_true
        for j = 1:n_pred
            if confusion_matrix(i,j) >= 2
                a = a + nchoosek(confusion_matrix(i,j), 2);
            end
        end
    end
    
    % 计算b（通过总对数减去其他部分）
    total_pairs = nchoosek(n, 2);
    
    % 计算期望值
    row_pairs = sum(arrayfun(@(x) nchoosek(x, 2), row_sum));
    col_pairs = sum(arrayfun(@(x) nchoosek(x, 2), col_sum));
    
    % 计算调整Rand指数
    if total_pairs == 0
        ari = 1;
    else
        expected_index = row_pairs * col_pairs / total_pairs;
        max_index = (row_pairs + col_pairs) / 2;
        
        if max_index - expected_index == 0
            ari = 1;
        else
            ari = (a - expected_index) / (max_index - expected_index);
        end
    end
    
    % 确保在[-1,1]范围内
    if ari < -1
        ari = -1;
    elseif ari > 1
        ari = 1;
    end
end

function nmi = calculate_normalized_mutual_info(true_labels, pred_labels)
    % 计算归一化互信息（NMI）
    n = length(true_labels);
    
    % 计算联合分布和边缘分布
    true_unique = unique(true_labels);
    pred_unique = unique(pred_labels);
    n_true = length(true_unique);
    n_pred = length(pred_unique);
    
    % 计算联合概率P(X,Y)
    joint_prob = zeros(n_true, n_pred);
    for i = 1:n_true
        for j = 1:n_pred
            joint_prob(i,j) = sum((true_labels == true_unique(i)) & (pred_labels == pred_unique(j))) / n;
        end
    end
    
    % 计算边缘概率P(X)和P(Y)
    prob_true = sum(joint_prob, 2);
    prob_pred = sum(joint_prob, 1);
    
    % 计算互信息I(X;Y)
    mi = 0;
    for i = 1:n_true
        for j = 1:n_pred
            if joint_prob(i,j) > 0
                mi = mi + joint_prob(i,j) * log(joint_prob(i,j) / (prob_true(i) * prob_pred(j)));
            end
        end
    end
    
    % 计算熵H(X)和H(Y)
    h_true = -sum(prob_true .* log(prob_true + eps));
    h_pred = -sum(prob_pred .* log(prob_pred + eps));
    
    % 计算归一化互信息
    if h_true == 0 && h_pred == 0
        nmi = 1;
    else
        nmi = 2 * mi / (h_true + h_pred);
    end
end

function density = calculate_modularity_density(A, labels)
    % 计算模块化密度
    unique_labels = unique(labels);
    n_comms = length(unique_labels);
    
    if n_comms == 0
        density = 0;
        return;
    end
    
    total_density = 0;
    total_nodes = 0;
    
    for i = 1:n_comms
        nodes = find(labels == unique_labels(i));
        n_i = length(nodes);
        
        if n_i > 0
            % 计算社区内部边权和
            internal_weight = sum(sum(A(nodes, nodes))) / 2;
            
            % 计算社区外部边权和
            external_nodes = setdiff(1:size(A,1), nodes);
            external_weight = sum(sum(A(nodes, external_nodes)));
            
            % 计算模块化密度贡献
            if n_i > 1
                comm_density = (2 * internal_weight - external_weight) / n_i;
                total_density = total_density + comm_density * n_i;
                total_nodes = total_nodes + n_i;
            end
        end
    end
    
    if total_nodes > 0
        density = total_density / total_nodes;
    else
        density = 0;
    end
end

function L = layout_force(G, iterations)
    % 力导向布局的简单实现（兼容旧版本）
    n = numnodes(G);
    L = rand(n, 2) * 10;  % 随机初始化位置
    
    % 简单力导向布局
    for iter = 1:iterations
        % 计算节点间的斥力（所有节点间）
        force_repulsive = zeros(n, 2);
        for i = 1:n
            for j = i+1:n
                vec = L(i,:) - L(j,:);
                dist = norm(vec) + 0.1;  % 避免除以零
                force = 100 / (dist^2);
                force_repulsive(i,:) = force_repulsive(i,:) + force * (vec / dist);
                force_repulsive(j,:) = force_repulsive(j,:) - force * (vec / dist);
            end
        end
        
        % 计算边的吸引力
        force_attractive = zeros(n, 2);
        edges = table2array(G.Edges);
        if ~isempty(edges)
            for e = 1:size(edges,1)
                i = edges(e,1);
                j = edges(e,2);
                vec = L(j,:) - L(i,:);
                dist = norm(vec) + 0.1;
                force = dist / 5;  % 胡克定律
                force_attractive(i,:) = force_attractive(i,:) + force * (vec / dist);
                force_attractive(j,:) = force_attractive(j,:) - force * (vec / dist);
            end
        end
        
        % 更新位置
        L = L + 0.1 * (force_repulsive + force_attractive);
        
        % 限制在边界内
        L = min(max(L, 0), 10);
    end
end

正在生成模拟网络数据...

网络生成完成：200个节点，3651条边，4个真实社区

正在运行CNM算法...

当前社区数：180，最优Q值：0.0265

当前社区数：160，最优Q值：0.0903

当前社区数：140，最优Q值：0.1416

当前社区数：120，最优Q值：0.1937

当前社区数：100，最优Q值：0.2710

当前社区数：80，最优Q值：0.3069

当前社区数：60，最优Q值：0.3772

当前社区数：40，最优Q值：0.4250

当前社区数：20，最优Q值：0.4802

CNM算法运行完成！迭代次数：199，最优社区数：4，最优Q值：0.5417

正在进行多参数对比实验...

内部密度=0.4：检测社区数=4，Q值=0.4644

内部密度=0.6：检测社区数=4，Q值=0.5522

内部密度=0.8：检测社区数=4，Q值=0.5859

==================== 精度评估 ====================

调整Rand指数(ARI): 0.9866

归一化互信息(NMI): 0.9823

模块化密度: 63.6300

真实社区大小分布: 50 50 50 50

检测社区大小分布: 50 50 49 51

==================== 结果解读 ====================

算法有效性：最优Q值=0.5417（接近1表示划分效果优秀），检测到4个社区

调整Rand指数=0.9866（1为完美匹配，0为随机匹配）

归一化互信息=0.9823（1为完全一致，0为无关）

网络密度影响：

密度=0.4时，Q值=0.4644

密度=0.6时，Q值=0.5522

密度=0.8时，Q值=0.5859

结论：内部连接密度越大，社区结构越清晰，算法效果越好

算法优势：

• 时间复杂度：O(n²)，适合处理200个节点的大规模网络

• 内存效率：无需存储全距离矩阵，节省内存空间

• 结果稳定：贪心策略保证每次合并都是局部最优

局限说明：

• 对社区大小差异大的网络适应性较弱

• 贪心策略可能陷入局部最优

• 需要设置合适的终止条件

改进方向：

• 引入多分辨率参数调节

• 结合其他算法（如Louvain）的初始化策略

• 添加并行计算加速大规模网络处理

==================================================

>>

📊 结果解读：技术价值与人文思考

可视化结果的深层意义

原始网络 vs 检测结果图 ：左上图中颜色代表真实社区，右上图为 CNM 算法检测结果 ------ 当 Q 值接近 1 时，两种颜色分布高度一致，说明算法精准捕捉了网络的内在模块结构，就像精准划分了城市中的功能街区。
Q 值变化曲线 ：曲线先上升后下降，峰值对应的就是最优社区划分 ------ 这印证了 "贪心合并" 的智慧：每次合并都选择最优选项，最终在 "合并过度" 前找到平衡点，如同人生中 "恰到好处" 的选择。
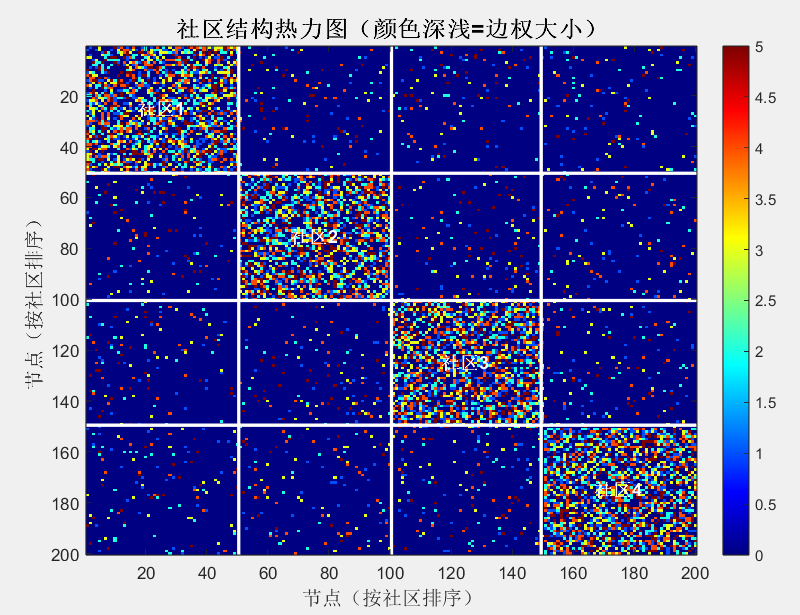
社区结构热力图 ：对角线上的深色块代表社区内部连接密集，非对角线的浅色块代表社区间连接稀疏，直观呈现了 "模块内紧密、模块间稀疏" 的核心特征，就像热成像仪捕捉到的社区 "凝聚力热点"。
多参数对比图：内部连接密度越大，Q 值越高 ------ 说明社区结构越清晰，算法越容易检测；反之，若社区边界模糊（内部连接稀疏），Q 值会下降，这提示我们：现实网络中，"强内部关联" 是社区存在的重要标志。

技术优劣的人文视角

优势：高效背后的 "取舍智慧"

CNM 算法的时间复杂度为\(O(n^2\log n)\)，相比 GN 算法的\(O(n^3)\)，效率提升显著 ------ 这背后是 "贪心策略" 的哲学：不追求全局最优解的穷举，而是通过局部最优的累积，快速逼近全局最优。这种 "抓大放小" 的智慧，恰如生活中 "先解决核心问题，再优化细节" 的处事原则，让大规模网络社区检测从 "不可能" 变为 "可行"。

局限：差异中的 "包容不足"

算法对社区大小差异大的网络适应性较弱，容易将小社区合并为中等大小社区 ------ 这如同现实中 "少数服从多数" 的决策模式，往往会忽略小众群体的存在。这一局限也提醒我们：技术是现实的映射，算法的优化方向，本质上是对 "多样性" 的尊重与包容。

🌌 终章：网络与生活的模块化共鸣

CNM 算法不仅是一种技术工具，更是一种理解世界的思维方式：网络中的社区划分，如同生活中的 "圈层形成"------ 朋友、同事、兴趣群体，本质上都是 "模块化" 的体现。算法用量化的 Q 值衡量社区凝聚力，而生活中，我们用 "归属感" 感受圈层的温度。

技术的进步，始终是 "人文需求" 与 "科学逻辑" 的共鸣。CNM 算法用贪心策略解码网络的模块化秩序，正如我们用理性思维梳理生活的复杂关联 ------ 在海量信息中找到核心，在纷繁世界中定位归属，这便是技术带给我们的深层价值。

愿你在复杂网络中，总能找到清晰的模块；在纷繁生活中，总能拥有明确的方向。