[优选算法专题十一.字符串 ——NO.60~63 最长公共前缀、5最长回文子串、二进制求和、字符串相乘]

题目链接

14. 最长公共前缀

题目描述

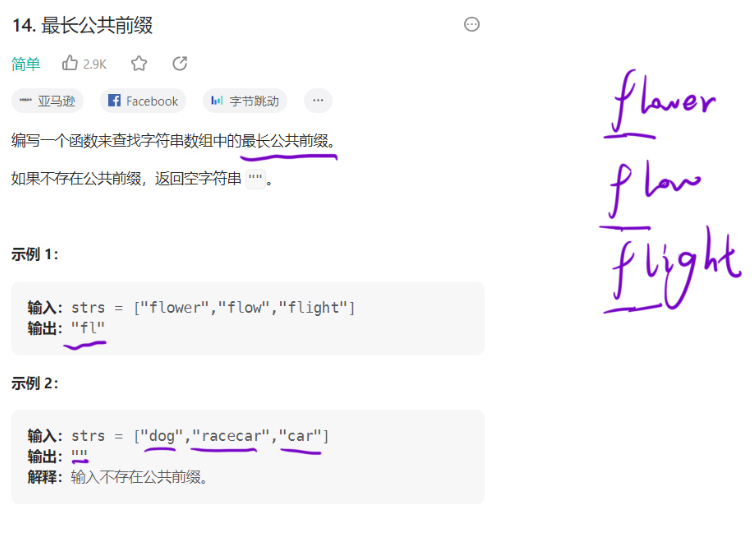
题目解析

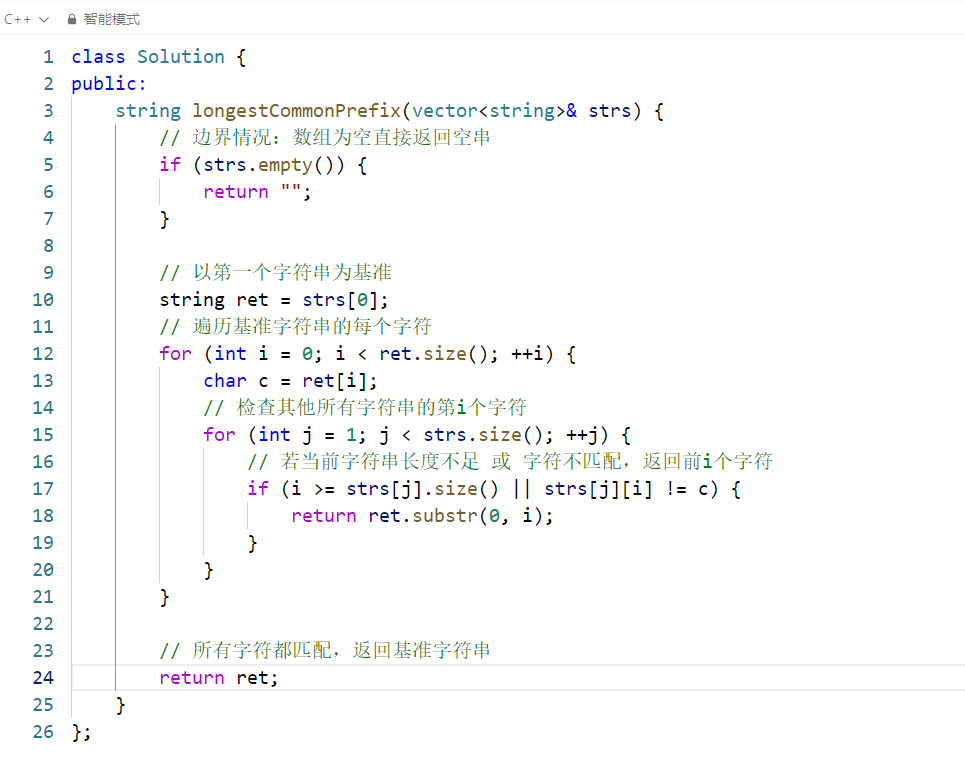
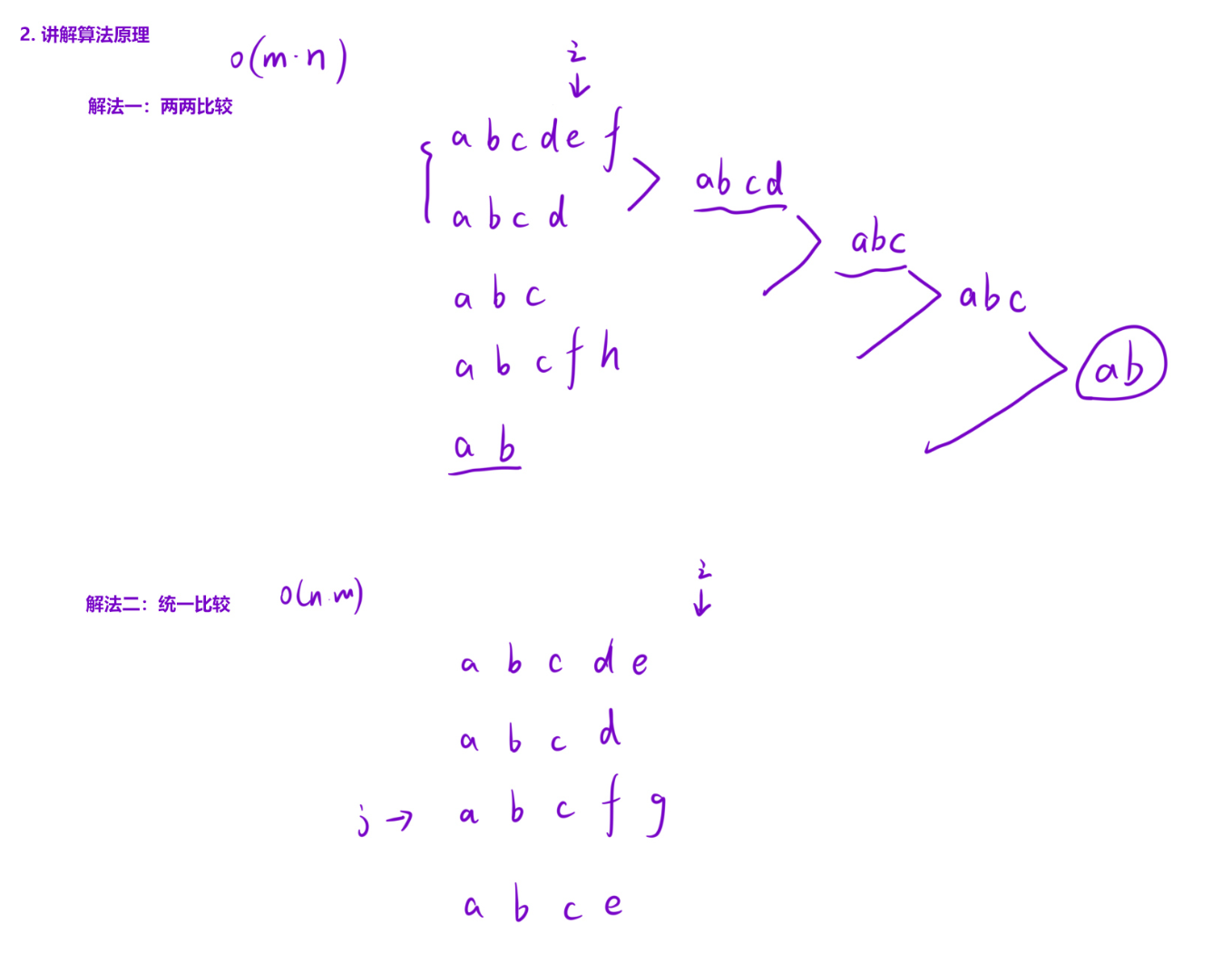
代码整体逻辑解析

该代码的核心思路是以第一个字符串为基准，逐字符校验其他所有字符串的对应位置，一旦发现不匹配或某个字符串长度不足，立即返回已匹配的前缀；若全部匹配完成，则返回基准字符串。

逐行详细解析

cpp 复制代码

class Solution {
public:
    string longestCommonPrefix(vector<string>& strs) {
        // 边界情况：数组为空直接返回空串
        if (strs.empty()) {
            return "";
        }

首先处理边界条件 ：如果输入的字符串数组 strs 为空（比如 strs = []），直接返回空字符串 ""，因为没有任何字符串，自然不存在公共前缀。

cpp 复制代码

        // 以第一个字符串为基准
        string ret = strs[0];

定义结果变量 ret，初始化为数组的第一个字符串。后续所有校验都以这个字符串的字符为 "标准"，因为最长公共前缀必然是第一个字符串的前缀（否则不可能是所有字符串的公共前缀）。

cpp 复制代码

        // 遍历基准字符串的每个字符
        for (int i = 0; i < ret.size(); ++i) {
            char c = ret[i];

外层循环：遍历基准字符串 ret 的每一个字符，i 是字符的索引，c 是当前遍历到的基准字符（比如 ret = "flower" 时，i=0 时 c='f'，i=1 时 c='l'）。

cpp 复制代码

            // 检查其他所有字符串的第i个字符
            for (int j = 1; j < strs.size(); ++j) {

内层循环：遍历数组中除第一个外的所有字符串 （j 从 1 开始），检查每个字符串的第 i 个字符是否和基准字符 c 一致。

cpp 复制代码

                // 若当前字符串长度不足 或 字符不匹配，返回前i个字符
                if (i >= strs[j].size() || strs[j][i] != c) {
                    return ret.substr(0, i);
                }
            }
        }

核心判断逻辑（触发返回的条件） ：
1. i >= strs[j].size()：当前字符串 strs[j] 的长度小于 i+1（比如基准字符串是 "flower"（长度 6），而 strs[j] 是 "flow"（长度 4），当 i=4 时，strs[j] 没有第 4 个字符），说明该字符串的长度已不足以匹配基准字符串的第 i 位，公共前缀只能到第 i 位之前。
2. strs[j][i] != c：当前字符串 strs[j] 的第 i 个字符和基准字符 c 不匹配（比如基准字符是 'o'（i=2），而 strs[j] 是 "flight"，其第 2 位是 'i'），说明公共前缀到第 i 位之前截止。
满足任一条件时，调用 ret.substr(0, i) 返回基准字符串的前 i 个字符（substr(起始索引, 长度)，这里起始索引 0，长度 i，即前 i 个字符）。

cpp 复制代码

        // 所有字符都匹配，返回基准字符串
        return ret;
    }
};

如果外层循环完整执行完毕（即基准字符串的所有字符都在其他字符串的对应位置匹配成功），说明基准字符串本身就是所有字符串的最长公共前缀，直接返回 ret。

关键特性总结

时间复杂度 ：O (m*n)，其中 m 是基准字符串的长度，n 是数组中字符串的数量。最坏情况下需要遍历基准字符串的所有字符，且每个字符都要校验所有其他字符串。
空间复杂度 ：O (1)，仅使用了常数个临时变量（ret、c、i、j），没有额外开辟与输入规模相关的空间。
提前终止：一旦发现不匹配或长度不足，立即返回结果，无需遍历全部字符，优化了实际执行效率。
边界覆盖：处理了 "空数组""单元素数组""字符串长度不一致""完全匹配" 等所有典型场景。

题目链接

5. 最长回文子串

题目描述

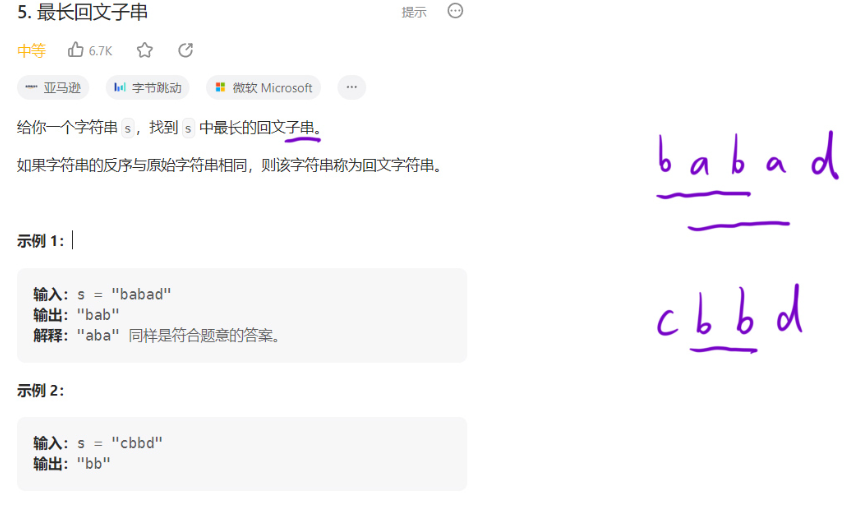
题目解析

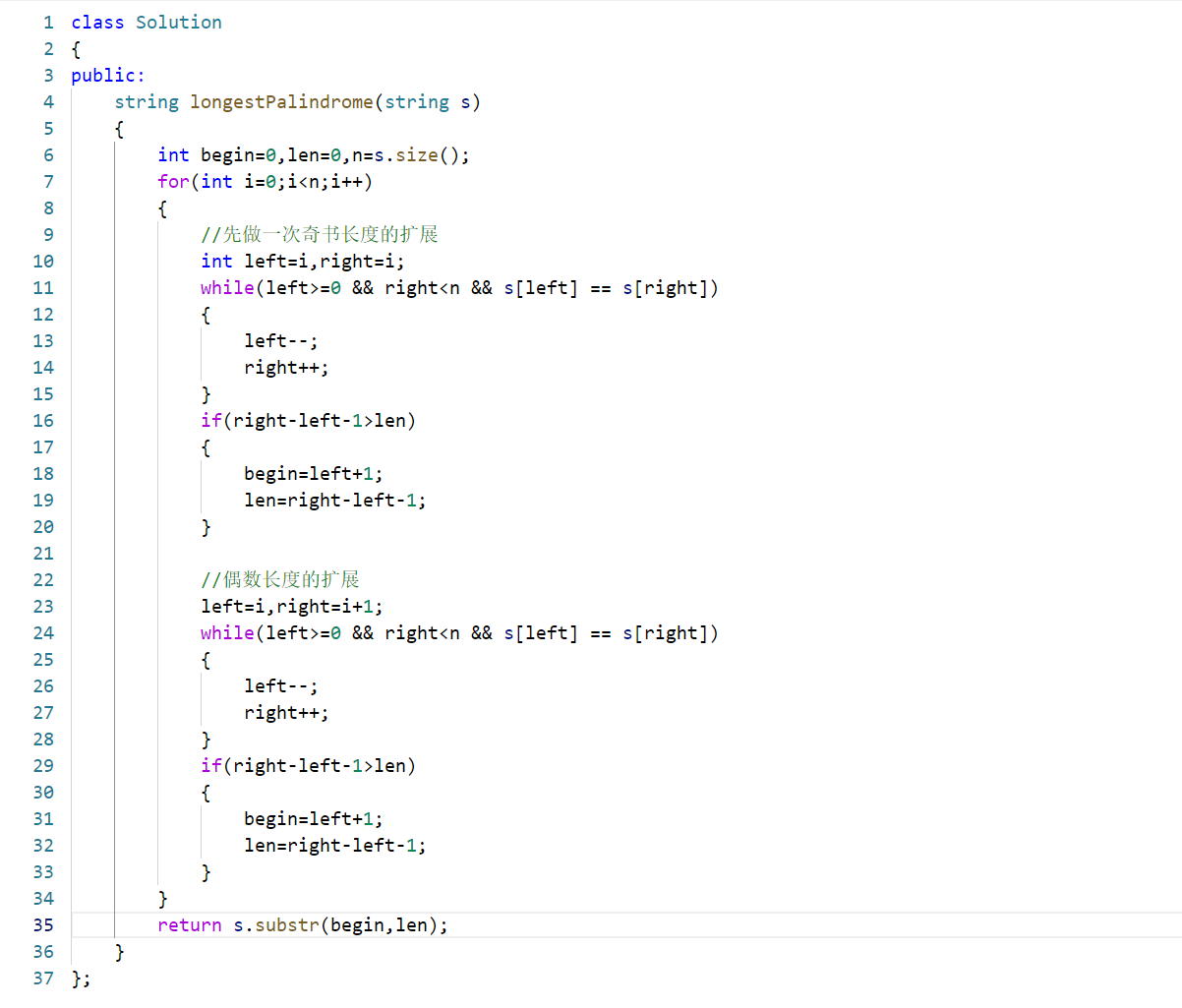
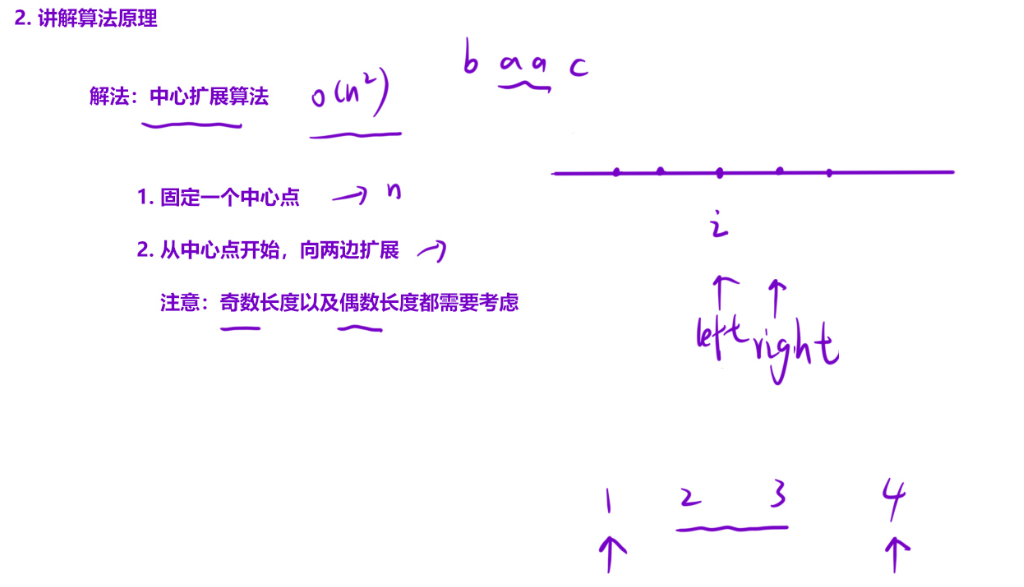
代码整体逻辑解析

该代码采用经典的中心扩展法求解最长回文子串，核心思路是：回文子串的中心有两种形式（奇数长度以单个字符为中心、偶数长度以两个相邻字符为中心），遍历字符串的每个位置，分别以该位置为「奇数中心」、该位置与下一个位置为「偶数中心」向左右扩展，记录每次扩展得到的最长回文子串的起始位置和长度，最终截取结果。

逐行详细解析

cpp 复制代码

class Solution 
{
public:
    string longestPalindrome(string s) 
    {
        int begin=0,len=0,n=s.size();

变量初始化 ：
- begin：记录最长回文子串的起始索引（初始为 0）；
- len：记录最长回文子串的长度（初始为 0，后续会被有效长度覆盖）；
- n：字符串 s 的长度，提前计算避免重复调用 s.size()。

cpp 复制代码

        for(int i=0;i<n;i++)
        {
            //先做一次奇数长度的扩展
            int left=i,right=i;

外层循环遍历字符串的每个位置 i，作为回文中心的起点：
- 首先处理奇数长度的回文 ：将左右指针 left 和 right 都初始化为 i（以单个字符 s[i] 为中心）。

cpp 复制代码

            while(left>=0 && right<n && s[left] == s[right])
            {
                left--;
                right++;
            }

中心扩展逻辑（奇数） ：
- 循环条件：left 不越界（≥0）、right 不越界（<n）、s[left] == s[right]（左右字符相等，满足回文）；
- 每次循环将 left 左移、right 右移，直到不满足回文条件为止。
- 退出循环时，s[left] != s[right]，因此实际的回文子串范围是 [left+1, right-1]。

cpp 复制代码

            if(right-left-1>len)
            {
                begin=left+1;
                len=right-left-1;
            }

更新最长回文信息（奇数） ：
- 计算当前扩展得到的回文长度：right - left - 1（推导：(right-1) - (left+1) + 1 = right - left - 1）；
- 若当前长度大于已记录的 len，说明找到更长的回文，更新 begin 为 left+1（回文起始位置），len 为当前长度。

cpp 复制代码

            //偶数长度的扩展
            left=i,right=i+1;

处理偶数长度的回文 ：将左指针初始化为 i，右指针初始化为 i+1（以两个相邻字符 s[i] 和 s[i+1] 为中心）。

cpp 复制代码

            while(left>=0 && right<n && s[left] == s[right])
            {
                left--;
                right++;
            }

中心扩展逻辑（偶数） ：
- 循环条件与奇数扩展一致：边界合法 + 左右字符相等；
- 同样向两侧扩展，直到不满足回文条件。

cpp 复制代码

            if(right-left-1>len)
            {
                begin=left+1;
                len=right-left-1;
            }
        }

更新最长回文信息（偶数） ：
- 计算当前偶数长度回文的长度（公式同奇数），若更长则更新 begin 和 len。

cpp 复制代码

        return s.substr(begin,len);
    }
};

返回结果 ：
- 调用 s.substr(begin, len) 截取从 begin 开始、长度为 len 的子串，即为最长回文子串。

关键细节补充

1. 长度计算公式推导

退出扩展循环时，left 和 right 是 "越界"/"不匹配" 的位置，因此实际回文的边界是 left+1（左边界）和 right-1（右边界）：

长度 = 右边界 - 左边界 + 1 = (right-1) - (left+1) + 1 = right - left - 1。

2. 初始值的合理性

len 初始为 0：若字符串为空（题目约束 s.length≥1，实际不会触发），返回空串；若字符串非空，第一次扩展（奇数）的长度至少为 1（单个字符），会覆盖初始的 0。
begin 初始为 0：若所有字符都不构成长回文（如 s="abc"），最终会截取 s[0,1]（即第一个字符），符合 "最长回文子串为单个字符" 的逻辑。

复杂度分析

时间复杂度：O (n²)，n 为字符串长度。每个字符最多向两侧扩展 n 次，共 n 个字符，总操作数为 n×n。
空间复杂度 ：O (1)，仅使用 begin、len、left、right 等常数个临时变量，无额外空间开销。

代码优势

逻辑直观：直接拆分奇数 / 偶数两种回文中心，无冗余封装，易于理解；
效率达标：时间复杂度 O (n²) 适配题目约束（n≤1000），实际运行效率高；
边界覆盖：自然处理 "单字符字符串""全相同字符字符串""无长回文（最长为 1）" 等所有场景。

题目链接

67. 二进制求和

题目描述

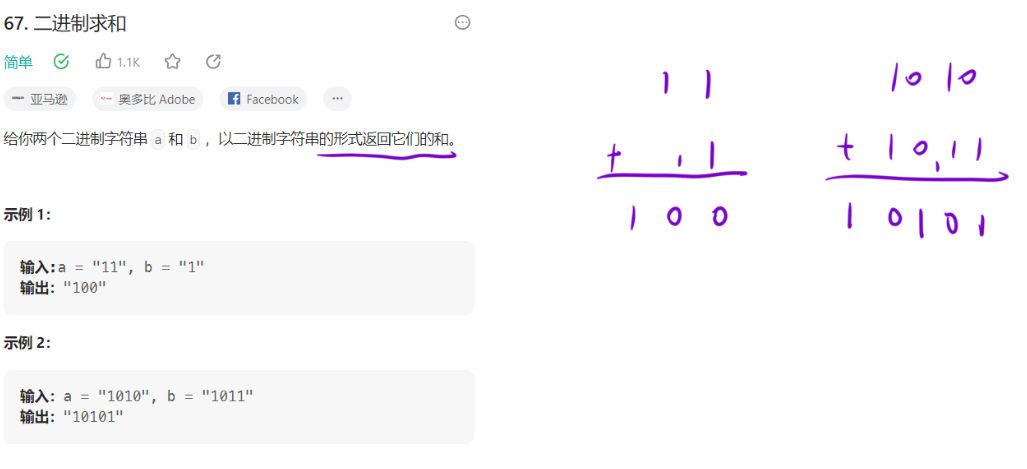
题目解析

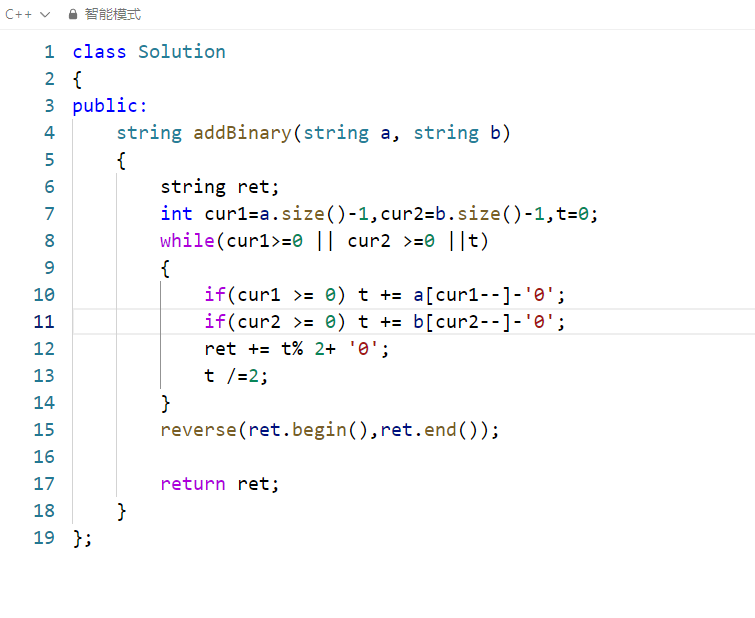
代码整体逻辑解析

该代码实现二进制字符串加法 的核心思路是：模拟手工计算二进制加法的过程------ 从两个二进制字符串的最低位（末尾）开始逐位相加，累加进位值，将每一位的计算结果暂存到结果字符串（逆序），最后反转结果得到正确顺序的二进制和。

整个过程完全贴合二进制加法规则：

每一位的和 = 第一个数的当前位 + 第二个数的当前位 + 上一位的进位；
当前位结果 = 总和 % 2（二进制取余）；
新的进位 = 总和 / 2（二进制整除）；
若所有位遍历完仍有进位，需额外添加进位位。

核心设计思路拆解

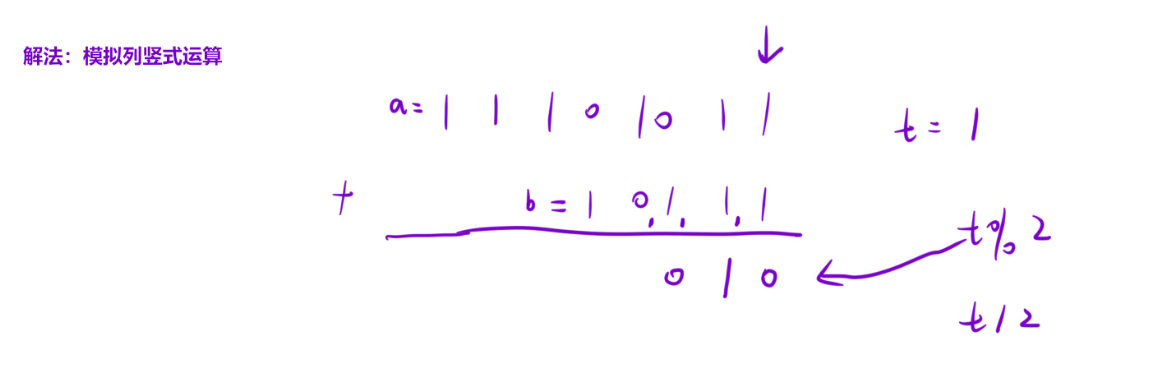
1. 指针与进位初始化

用 cur1/cur2 分别指向两个字符串的最低位（末尾），从后往前遍历（符合手工加法 "从低位到高位" 的习惯）；
用 t 同时存储 "当前位总和 + 进位"，初始为 0（无初始进位）。

2. 循环终止条件

while(cur1>=0 || cur2 >=0 ||t) 覆盖三种必须继续计算的场景：

cur1>=0：字符串 a 还有未计算的位；
cur2>=0：字符串 b 还有未计算的位；
t≠0：所有位计算完但仍有进位（如 a="1"、b="1"，相加后需额外添加进位位 1）。

3. 逐位计算逻辑

字符转整数：a[cur1]-'0'/b[cur2]-'0' 将字符形式的二进制位（'0'/'1'）转为整数（0/1），避免 ASCII 码直接相加的错误；
累加当前位：将 a/b 的当前位（若存在）累加到 t；
计算当前位结果：t%2 得到二进制当前位（0/1），+'0' 转回字符并追加到结果字符串；
更新进位：t/=2 取整除结果，作为下一位的进位（如 t=3 时，进位为 1；t=1 时，进位为 0）。

4. 结果修正

由于计算时从低位到高位存储结果（如 1010+1011=10101，暂存的结果是 10101 的逆序 10101 → 实际过程中先存 1、再 0、再 1、再 0、再 1），因此需要反转字符串得到正确顺序。

复杂度分析

时间复杂度 ：O (max (n,m))，n 和 m 分别为两个字符串的长度。最多遍历 max(n,m)+1 次（含进位位），反转操作的时间为 O (max (n,m))，整体为线性时间。
空间复杂度 ：O (max (n,m))，结果字符串的长度最多为 max(n,m)+1（含进位位），仅使用常数额外变量，空间开销由结果字符串主导。

题目链接

43. 字符串相乘

题目描述

题目解析

字符串相乘算法解析

这个算法的核心思路是模拟手工乘法的计算过程：先不考虑进位完成所有位的相乘累加，再统一处理进位，最后处理前导零并调整结果格式。下面分步骤拆解代码逻辑。

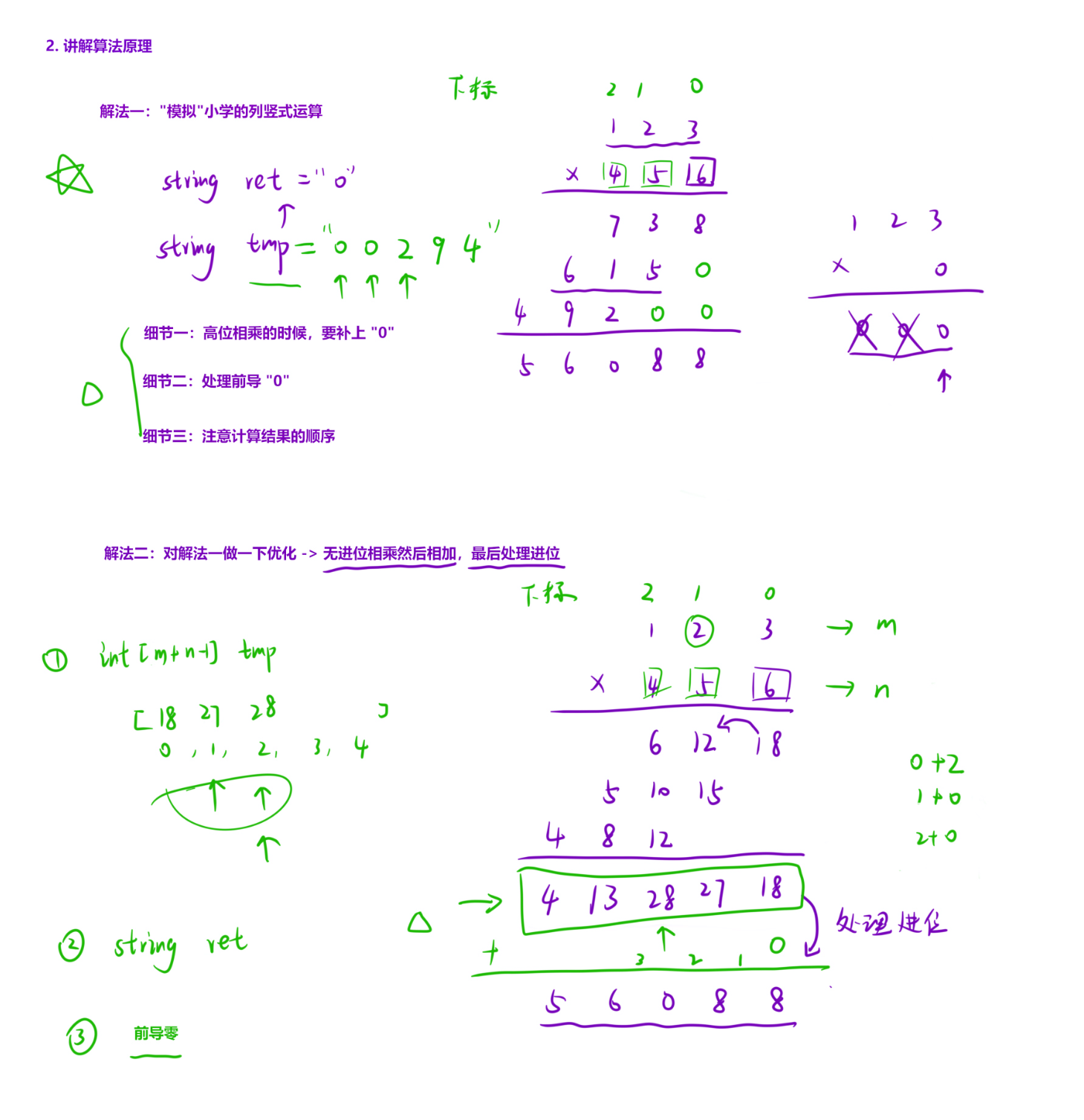
一、核心思路回顾

手工计算两个数相乘的过程：

对应到字符串乘法中：

逆序字符串，让低位（个位、十位）对应索引 0、1，方便按位计算；
无进位相乘：n1[i] × n2[j] 的结果累加到 tmp[i+j]（因为个位 × 个位 = 个位，个位 × 十位 = 十位，对应索引和）；
统一处理进位：遍历累加后的数组，将每一位的余数保留、商进位；
调整格式：去除前导零，逆序还原结果。

二、代码逐行解析

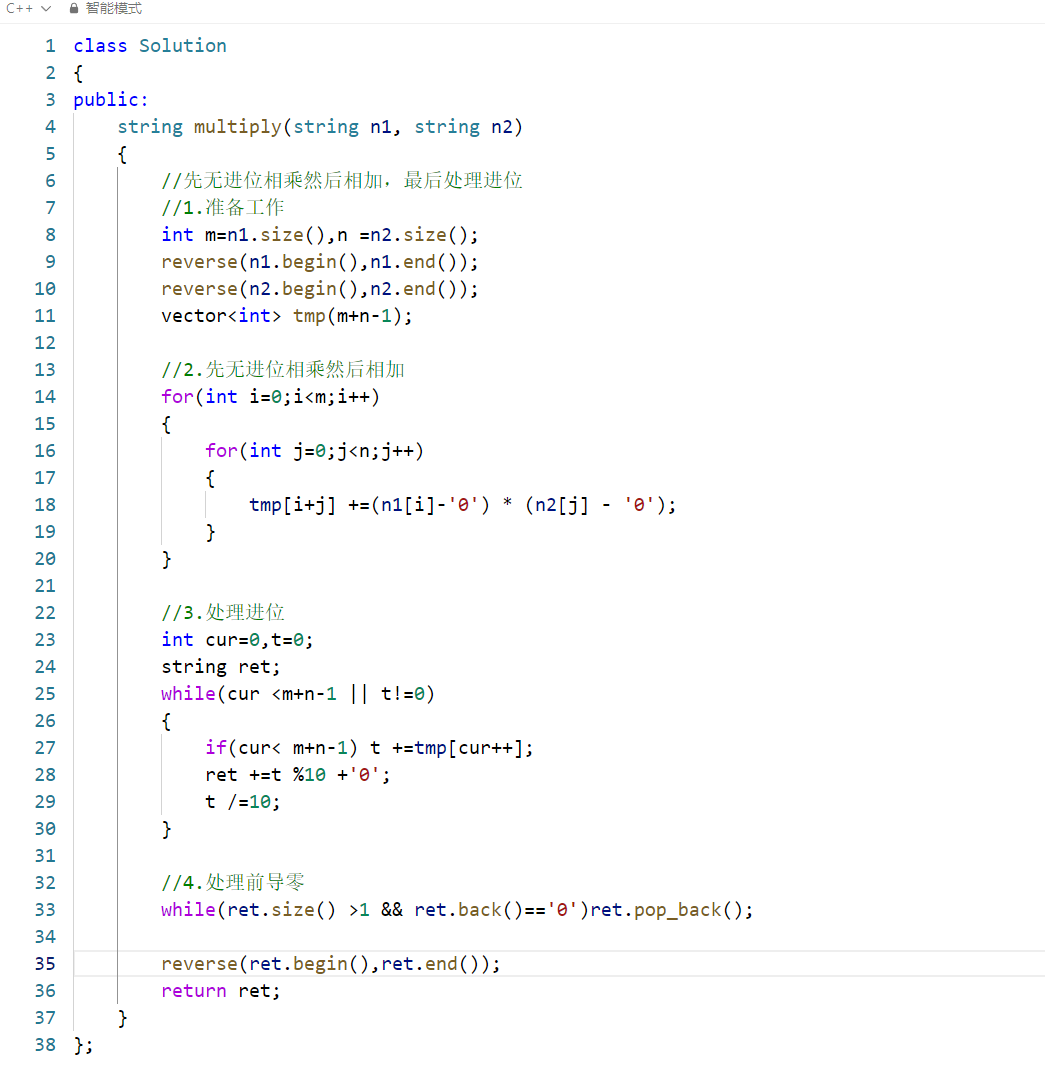
1. 准备工作

cpp 复制代码

int m = n1.size(), n = n2.size();
reverse(n1.begin(), n1.end());
reverse(n2.begin(), n2.end());
vector<int> tmp(m + n - 1);

m/n：分别是两个输入字符串的长度（即数字的位数）；
reverse：将字符串逆序，例如 "123" 逆序为 "321"，让低位（个位）对应索引 0，符合数组从 0 开始的遍历习惯；
tmp 数组：长度为 m+n-1（两个数相乘的最大位数是 m+n，无进位时最多 m+n-1 位），用于存储 "无进位相乘累加" 的结果。

2. 无进位相乘 + 累加

cpp 复制代码

for(int i=0;i<m;i++) {
    for(int j=0;j<n;j++) {
        tmp[i+j] += (n1[i]-'0') * (n2[j] - '0');
    }
}

双层循环遍历两个逆序后的字符串的每一位；
n1[i]-'0'/n2[j]-'0'：将字符转为对应的数字（如 '9'->9）；
tmp[i+j] += ...：核心逻辑 ------
- 例如：n1 的第 i 位（对应 10^i 位） × n2 的第 j 位（对应 10^j 位）= 结果的 10^(i+j) 位，因此累加到tmp[i+j]；
- 无进位：只累加乘积，不处理超过 9 的情况（例如 12 先存在 tmp 里，后续统一进位）。

3. 处理进位

cpp 复制代码

int cur=0,t=0;
string ret;
while(cur <m+n-1 || t!=0) {
    if(cur< m+n-1) t +=tmp[cur++]; // 累加当前位的无进位值
    ret += t %10 +'0'; // 保留个位（余数），转为字符
    t /=10; // 进位（商），留给下一位处理
}

cur：遍历 tmp 数组的指针；t：当前位的总数值（包含上一位的进位）；
循环条件：cur < m+n-1（还有未处理的无进位位）或 t!=0（还有未处理的进位）；
核心操作：
1. 累加当前 tmp 位的值到t；
2. t%10：取个位（最终保留在当前位的数字），转为字符存入结果；
3. t/10：取十位及以上（进位），留给下一位处理；
示例：若t=12，则12%10=2（当前位），12/10=1（进位到下一位）。

4. 处理前导零 + 逆序还原

cpp 复制代码

while(ret.size() >1 && ret.back()=='0') ret.pop_back();
reverse(ret.begin(),ret.end());
return ret;

处理前导零：
- 因为结果是逆序存储 的（个位在前，高位在后），所以ret.back()是结果的最高位；
- 例如：若结果是0005（逆序后是5000），则ret.back()是0，需要循环删除，直到最高位非零或只剩 1 位；
逆序还原：因为之前的结果是 "个位在前、高位在后"，逆序后恢复为 "高位在前、个位在后" 的正常顺序。

四、边界情况处理

其中一个数为 0：例如n1="0", n2="123" → tmp 全 0 → ret="0000" → 处理前导零后只剩 "0"；
两个数都是个位数：例如n1="9", n2="9" → tmp [0]=81 → 进位后 ret="18"（逆序前是 "81"，逆序后 "18"）；
结果有多位进位：例如n1="999", n2="999" → 结果为 "998001"，算法能正确处理连续进位。

五、算法复杂度

时间复杂度：O (m×n)，双层循环遍历两个字符串的每一位，后续处理为线性时间；
空间复杂度：O (m+n)，tmp 数组和结果字符串的长度均为 m+n 级别。

该算法是字符串乘法的经典实现，核心是 "无进位累加 + 统一进位"，避免了逐位处理进位的繁琐，逻辑清晰且效率较高。

[优选算法专题十一.字符串 ——NO.60~63 最长公共前缀、5最长回文子串、 二进制求和 、字符串相乘]

题目链接

14. 最长公共前缀

题目描述

题目解析

代码整体逻辑解析

逐行详细解析

关键特性总结

题目链接

5. 最长回文子串

题目描述

题目解析

代码整体逻辑解析

逐行详细解析

关键细节补充

1. 长度计算公式推导

2. 初始值的合理性

复杂度分析

代码优势

题目链接

67. 二进制求和

题目描述

题目解析

代码整体逻辑解析

核心设计思路拆解

1. 指针与进位初始化

2. 循环终止条件

3. 逐位计算逻辑

4. 结果修正

复杂度分析

题目链接

43. 字符串相乘

题目描述

题目解析

字符串相乘算法解析

一、核心思路回顾

二、代码逐行解析

1. 准备工作

2. 无进位相乘 + 累加

3. 处理进位

4. 处理前导零 + 逆序还原

四、边界情况处理

五、算法复杂度

[优选算法专题十一.字符串 ——NO.60~63 最长公共前缀、5最长回文子串、二进制求和、字符串相乘]