聚类方法（kmeans，DBSCAN，层次聚类，GMM，EM算法）

聚类算法概述

划分式聚类：
- K-Means
- - K值的选择
- K-means++（K++means）
- [Bisecting K-means（Bi-means）](#Bisecting K-means（Bi-means）)
基于密度的聚类：
- [DBSCAN（Density-Based Spatial Clustering of Applications with Noise）](#DBSCAN（Density-Based Spatial Clustering of Applications with Noise）)
- [OPTICS（Ordering Points To Identify the Clustering Structure）](#OPTICS（Ordering Points To Identify the Clustering Structure）)
[层次聚类（Hierarchical Clustering）](#层次聚类（Hierarchical Clustering）)
- - 常用距离定义
  - 簇间距离计算方法比较
高斯混合模型（GMM）
- EM（Expectation‑Maximization）算法
- [高斯混合模型（Gaussian Mixture Model，GMM）](#高斯混合模型（Gaussian Mixture Model，GMM）)

聚类是一种无监督学习方法，旨在将数据划分为具有相似特征的组（簇）。即聚类后同一类的数据尽可能聚集到一起，不同类数据尽量分离。以下是常见聚类算法及其核心思想和步骤：

划分式聚类：

K-Means

核心思想：通过最小化簇内平方误差（SSE）将数据划分为K个簇，每个簇由均值（质心）表示。
算法步骤
1. 随机初始化K个质心。
2. 将每个数据点分配到最近的质心所属簇。
3. 重新计算每个簇的质心（均值）。
4. 重复步骤2-3直到质心不再变化或达到最大迭代次数。
缺点
1. 对初始中心点敏感
2. 容易陷入局部最优
3. 对k值敏感

K值的选择

肘部图：观察不同K值下聚类模型的误差平方和（SSE）变化趋势，寻找拐点作为最佳K值。误差平方和随K值增大而减小，拐点处下降幅度显著减缓，形如手肘。
S S E = ∑ i = 1 k ∑ x ∈ C i ∣ ∣ x − μ i ∣ ∣ 2 SSE = \sum_{i=1}^{k} \sum_{x \in C_i} ||x - \mu_i||^2 SSE=i=1∑kx∈Ci∑∣∣x−μi∣∣2
其中， C i C_{i} Ci为第 i i i类， μ i \mu_{i} μi为 C i C_{i} Ci的类中心

代码实现：

python3 复制代码

from sklearn.cluster import KMeans
import matplotlib.pyplot as plt

sse = []
for k in range(1, 11):
    kmeans = KMeans(n_clusters=k, random_state=42).fit(X)
    sse.append(kmeans.inertia_)

plt.plot(range(1, 11), sse, marker='o')
plt.xlabel('K')
plt.ylabel('SSE')
plt.title('Elbow Method')
plt.show()

轮廓系数：衡量样本与自身簇和其他簇的相似度，取值范围[-1,1]，值越大表示聚类效果越好。最佳K值对应轮廓系数峰值。

轮廓系数计算： s ( i ) = b ( i ) − a ( i ) max ⁡ ( a ( i ) , b ( i ) ) s(i) = \frac{b(i) - a(i)}{\max\big(a(i), b(i)\big)} s(i)=max(a(i),b(i))b(i)−a(i)

其中, a ( i ) a(i) a(i) 是样本 i i i到其所属簇中其他样本的平均距离（反映簇的紧密性）。 b ( i ) b(i) b(i)是样本 i i i到最近的其他簇中样本的平均距离（反映簇间的分离性）。

K-means++（K++means）

核心思想 ：优化初始中心点的选择，减少随机性带来的影响。通过加权概率避免初始中心点过于集中，提升聚类效果和收敛速度。
核心改进 ：

初始中心点选择采用概率分布：第一个中心随机选取，后续中心点选择时，距离已选中心越远的点被选中的概率越高。

若已有中心点集合 C C C，新中心点 x x x的选择概率为：
P ( x ) = D ( x ) 2 ∑ x i ∈ X D ( x i ) 2 P(x) = \frac{D(x)^{2}}{\sum_{x_{i}\in X} D(x_{i})^{2}} P(x)=∑xi∈XD(xi)2D(x)2

其中 D ( x ) D(x) D(x) 是 x x x到最近中心点的距离。

Bisecting K-means（Bi-means）

核心思想：采用自上而下的二分策略：每次选择一个现有簇进行二分（使用K-means），直到达到预设的簇数 ( K )。选择分裂的簇时，通常选取误差平方和（SSE）最大的簇。

算法步骤：

将所有点视为一个簇

当簇的个数小于预设值K时

对每个簇

计算总SSE

在给定的簇上进行k-means聚类（k=2）

计算聚类后的两个簇的SSE总和

选择使SSE最小的簇进行划分（或者是能带来最大SSE降低的簇进行划分，类似于选择增益最大的簇进行划分）

优势：

更适合处理层次化结构的数据，如文档聚类。
相比传统K-means，对初始中心的依赖性更低。

基于密度的聚类：

DBSCAN（Density-Based Spatial Clustering of Applications with Noise）

核心思想：基于密度划分簇，能够发现任意形状的簇并识别噪声点。

算法步骤

定义邻域参数（ ε \varepsilon ε半径和最小点数 M M M）。
从核心点（邻域内点数≥ M M M）出发，扩展形成簇。
将密度可达的点归入同一簇，未被归类的点标记为噪声。

密度可达的含义：核心点邻域中的点，如果也满足其邻域内点数 ≥ M \ge M ≥M，则也是核心点。如果不是核心点，但在核心点的邻域内则称为边界点，否则为噪声

优点：不需要提前设置聚类的个数；对噪声不敏感

缺点：需要提前确定 ε \varepsilon ε-半径和最小点数 M M M；对初值选取敏感; 对密度不均的数据聚合效果不好

DBSCAN中使用了统一的 ε \varepsilon ε值，当数据密度不均匀的时候

较小的 ε \varepsilon ε值，则较稀疏的cluster中的节点密度会小于 M M M，会被认为是边界点而不被用于进一步的扩展；
较大的 ε \varepsilon ε值，则密度较大且离的比较近的cluster容易被划分为同一个cluster，如下图所示。

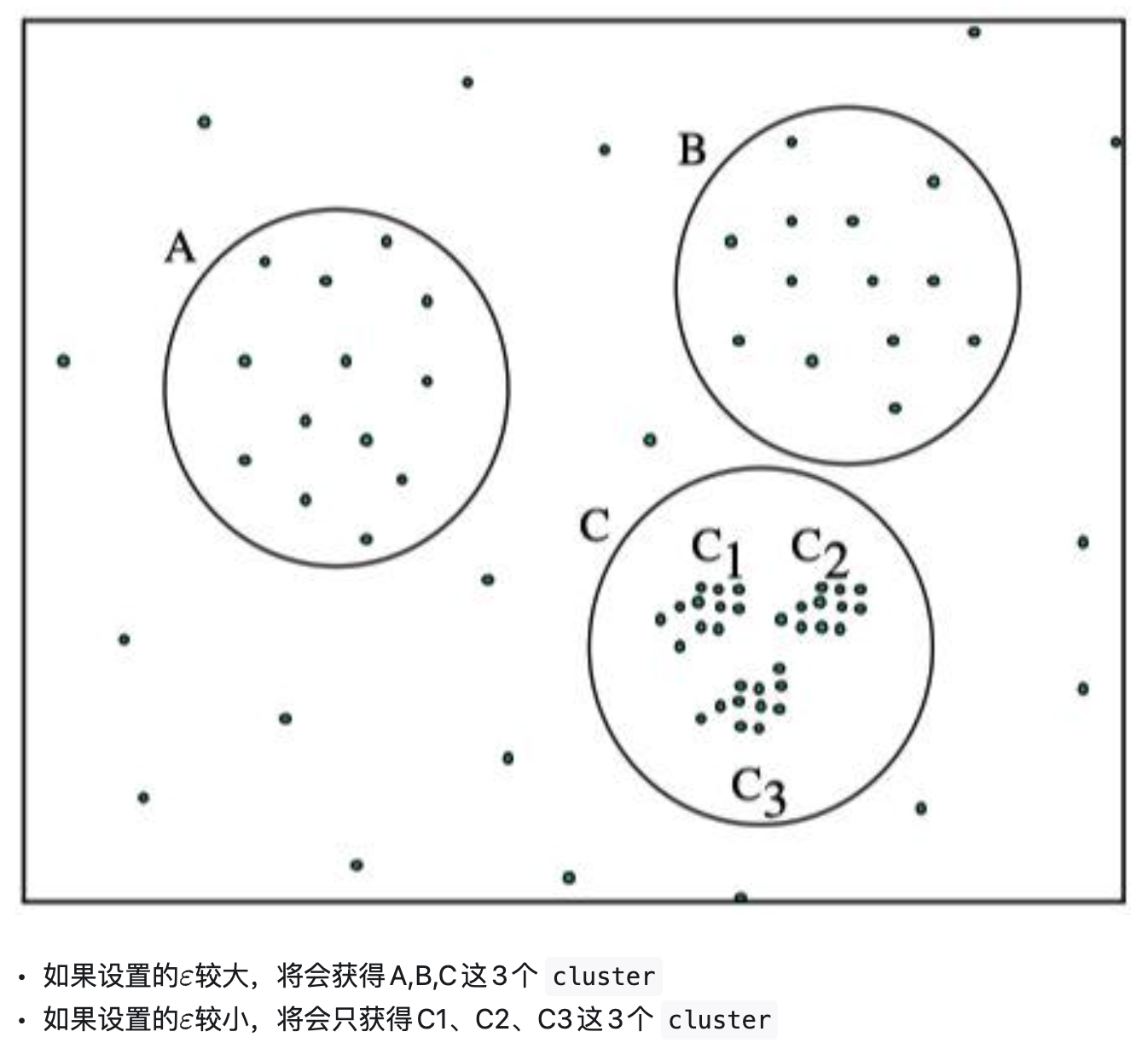
因此考虑合适的 ε \varepsilon ε值，即OPRTICS，解决对输入参数敏感的问题。即选取有限个邻域参数进行聚类，这样就能得到不同邻域参数下的聚类结果。

OPTICS（Ordering Points To Identify the Clustering Structure）

前提知识：

核心距离（Core Distance） ：

对于给定对象 p p p 和邻域半径 ε \varepsilon ε，核心距离是使得 p 成为核心点的最小距离。数学表示为：
C D ( p , ε ) = m i n { r ∣ r ≤ ε , ∣ N r ( p ) ∣ ≥ M i n P t s } CD(p, \varepsilon) = min\{r | r ≤ ε, |N_r(p)| ≥ MinPts\} CD(p,ε)=min{r∣r≤ε,∣Nr(p)∣≥MinPts}

其中： N r ( p ) N_{r}(p) Nr(p) 表示以 p p p 为中心、半径为 r r r 的邻域内包含的点的集合。MinPts 是预设的最小邻居数量阈值。若 ∣ N ε ( p ) ∣ < M i n P t s |N_{\varepsilon}(p)| < MinPts ∣Nε(p)∣<MinPts，则 p p p 非核心点，核心距离为未定义（ ∞ \infty ∞）。
可达距离（Reachability Distance）

对象 q q q 关于核心点 p p p 的可达距离定义为：
R D ( p , q , ε ) = m a x ( C D ( p , ε ) , d ( p , q ) ) RD(p, q, ε) = max(CD(p, ε), d(p, q)) RD(p,q,ε)=max(CD(p,ε),d(p,q))

其中： d ( p , q ) d(p, q) d(p,q)是 p p p 与 q q q 的直接距离（如欧氏距离）。若 p p p 非核心点，可达距离无意义（ ∞ \infty ∞）。
性质：

可达距离 ≥ \ge ≥核心距离。

通过可达距离可构建可达性图（Reachability Plot），直观展示簇结构。

算法通过优先队列处理对象的可达距离，生成有序的输出序列。

核心思想 ：改进DBSCAN，通过可达距离排序处理多密度簇。
算法步骤

计算每个点的核心距离和可达距离。
按可达距离生成排序列表。
基于排序列表和阈值提取簇结构。

具体：

初始化：所有对象标记为未处理，创建空的有序列表和优先队列（按可达距离排序）。
处理对象
1. 从未处理对象中选择一个种子点 p p p，计算其核心距离。若未定义，跳过；否则获取其 ϵ \epsilon ϵ-邻域。
2. 将 p p p加入有序列表，并计算邻域内每个点 q q q的可达距离，更新优先队列。
扩展聚类：从优先队列中提取可达距离最小的 q q q，重复上述步骤，直到队列为空。
生成可达距离图：输出有序列表及对应的可达距离，通过可视化或阈值提取聚类。（按照密度不同将相近密度的点聚合在一起，而不是输出该点所属的具体类别）

insert_list()函数定义如下：

层次聚类（Hierarchical Clustering）

核心思想：通过树状结构（树状图）逐步合并或分裂簇，分为凝聚式（自底向上）和分裂式（自顶向下）。

算法步骤（凝聚式）

将每个数据点视为单独簇。
计算簇间距离（如单链接、全链接、平均链接）。
合并距离最近的两个簇。
重复步骤2-3直到所有点聚为一个簇或达到终止条件。

常用距离定义

距离名称	定义	数学表达式（二维空间）	适用场景
欧氏距离	两点间的直线距离	d = ( x 2 − x 1 ) 2 + ( y 2 − y 1 ) 2 d = \sqrt{(x₂ - x₁)² + (y₂ - y₁)²} d=(x2−x1)2+(y2−y1)2	几何空间、聚类分析
曼哈顿距离	两点在坐标轴上的绝对距离之和	d = ∣ x 2 − x 1 ∣ + ∣ y 2 − y 1 ∣ d= \vert x_{2} - x_{1} \vert +\vert y_{2} - y_{1} \vert d=∣x2−x1∣+∣y2−y1∣	网格路径规划、图像处理
切比雪夫距离	两点各维度坐标差的最大值	d = m a x ( ∣ x 2 − x 1 ∣ , ∣ y 2 − y 1 ∣ ) d=max( \vert x_{2} - x_{1} \vert, \vert y_{2} - y_{1} \vert) d=max(∣x2−x1∣,∣y2−y1∣)	棋盘移动、像素分析
闵可夫斯基距离	欧氏和曼哈顿距离的广义形式（p为参数）	d = ( ∣ x 2 − x 1 ∣ p + ∣ y 2 − y 1 ∣ p ) 1 / p d= \big(\vert x_{2} - x_{1} \vert ^{p}+\vert y_{2} - y_{1} \vert^{p}\big)^{1/p} d=(∣x2−x1∣p+∣y2−y1∣p)1/p	灵活调整距离度量（p=1:曼哈顿；p=2:欧氏）
余弦相似度	通过向量夹角余弦值衡量方向相似性（非严格距离）	c o s θ = x 1 x 2 + y 1 y 2 ( x 1 2 + y 1 2 ) ∗ ( x 2 2 + y 2 2 ) cos\theta =\frac{x_{1}x_{2}+y_{1}y_{2}}{\sqrt{(x_{1}^{2}+y_{1}^{2})}*\sqrt{(x_{2}^{2}+y_{2}^{2})}} cosθ=(x12+y12) ∗(x22+y22) x1x2+y1y2	文本分类、推荐系统
马氏距离	考虑数据协方差结构的标准化距离	d = ( ( x 2 − x 1 ) T Σ − 1 ( x 2 − x 1 ) ) d = \sqrt{((x₂ - x₁)ᵀΣ⁻¹(x₂ - x₁))} d=((x2−x1)TΣ−1(x2−x1)) （ Σ Σ Σ为协方差矩阵）	多元统计、异常检测
汉明距离	两个等长字符串在相同位置不同字符的数量	d = Σ δ ( x i ≠ y i ) d = Σδ(xᵢ ≠ yᵢ) d=Σδ(xi=yi)（ δ δ δ为指示函数）	编码理论、DNA序列比对
杰卡德距离	1减去杰卡德相似系数（集合差异度量）	d = 1 − ∣ A ∩ B ∣ ∣ A ∪ B ∣ d=1-\frac{\vert A\cap B\vert }{\vert A\cup B\vert} d=1−∣A∪B∣∣A∩B∣	集合相似度、推荐系统

闵可夫斯基距离 是通用形式，通过调整参数p可衍生其他距离。
余弦相似度 通常用于方向相似性，需转换为1 - cosθ作为距离度量。
马氏距离对数据分布敏感，适用于非独立同分布数据。

簇间距离计算方法比较

以下表格总结了单链接、全链接、平均链接三种常见的簇间距离计算方法，包括计算公式、优缺点及适用场景：

方法	计算公式	优点	缺点	适用场景
单链接	D ( A , B ) = min ⁡ a ∈ A , b ∈ B d ( a , b ) D(A,B) = \min_{a \in A, b \in B} d(a,b) D(A,B)=mina∈A,b∈Bd(a,b)	能发现非球形簇；对噪声敏感度低	易形成链式簇（Chaining Effect）	细长或不规则形状的簇
全链接	D ( A , B ) = max ⁡ a ∈ A , b ∈ B d ( a , b ) D(A,B) = \max_{a \in A, b \in B} d(a,b) D(A,B)=maxa∈A,b∈Bd(a,b)	生成的簇更紧凑，避免链式效应	对噪声和离群点敏感	球形或紧凑簇
平均链接	D ( A , B ) = 1 ∣ A ∣ ∗ ∣ B ∣ ∑ a ∈ A ∑ b ∈ B d ( a , b ) D(A,B) = \frac{1}{\vert A\vert* \vert B\vert} \sum_{a \in A} \sum_{b \in B} d(a,b) D(A,B)=∣A∣∗∣B∣1∑a∈A∑b∈Bd(a,b)	平衡单链接和全链接的特性	计算复杂度较高	通用场景，尤其是中等规模数据集

高斯混合模型（GMM）

核心思想：假设数据由多个高斯分布混合生成，通过EM算法估计参数。

算法步骤

初始化高斯分布的参数（均值、协方差、权重）。
E步：计算每个点属于各高斯分布的后验概率。
M步：更新高斯分布的参数以最大化似然函数。
重复E-M步骤直到收敛。

EM（Expectation‑Maximization）算法

问题背景

在许多无监督学习任务中，模型的 完整数据 包含可观测变量 (X) 与 隐变量 (Z)。直接对观测数据求极大似然往往难以解析，因为似然函数涉及对隐变量的积分或求和。
算法框架

EM 通过交替进行两步迭代来间接优化参数 (\theta)：
- E 步（Expectation） ：在当前参数 θ ( t ) \theta^{(t)} θ(t) 下，计算隐变量的后验分布 p ( Z ∣ X , θ ( t ) ) p(Z|X,\theta^{(t)}) p(Z∣X,θ(t))，并求出 对数似然的条件期望
  Q ( θ ∣ θ ( t ) ) = E Z ∣ X , θ ( t ) ⁣ [ log ⁡ p ( X , Z ∣ θ ) ] . Q(\theta|\theta^{(t)}) = \mathbb{E}_{Z\mid X,\theta^{(t)}}\!\big[\log p(X,Z|\theta)\big]. Q(θ∣θ(t))=EZ∣X,θ(t)[logp(X,Z∣θ)].
- M 步（Maximization） ：最大化上式得到新的参数
  θ ( t + 1 ) = arg ⁡ max ⁡ θ Q ( θ ∣ θ ( t ) ) . \theta^{(t+1)} = \arg\max_{\theta} Q(\theta|\theta^{(t)}). θ(t+1)=argθmaxQ(θ∣θ(t)).
  迭代过程保证对数似然单调不减，最终收敛到局部极大值。
适用范围
- 参数中出现 缺失/隐变量（如聚类标签、混合模型的成分指示、隐马尔可夫模型的状态序列）。
- 需要 极大似然估计 或 最大后验估计 的生成模型。

高斯混合模型（Gaussian Mixture Model，GMM）

模型假设

GMM 认为观测数据由 K K K 个多元正态分布 的线性混合生成：
p ( x ) = ∑ k = 1 K π k N ( x ∣ μ k , Σ k ) , p(x)=\sum_{k=1}^{K}\pi_k\;\mathcal{N}(x|\mu_k,\Sigma_k), p(x)=k=1∑KπkN(x∣μk,Σk),

其中 π k \pi_k πk 为混合权重（满足 ∑ k π k = 1 \sum_k\pi_k=1 ∑kπk=1， μ k , Σ k \mu_k,\Sigma_k μk,Σk 分别是第 (k) 个高斯分量的均值向量和协方差矩阵。
参数估计

由于每个样本的 分量指示变量（即它属于哪一个高斯）是不可观测的，GMM 的参数估计天然适用 EM：
- E 步 ：计算每个样本属于第 k k k 个分量的后验概率（软分配）
  γ i k = p ( z i = k ∣ x i , θ ( t ) ) = π k ( t ) N ( x i ∣ μ k ( t ) , Σ k ( t ) ) ∑ j = 1 K π j ( t ) N ( x i ∣ μ j ( t ) , Σ j ( t ) ) . \gamma_{ik}=p(z_i=k|x_i,\theta^{(t)})= \frac{\pi_k^{(t)}\mathcal{N}(x_i|\mu_k^{(t)},\Sigma_k^{(t)})} {\sum_{j=1}^{K}\pi_j^{(t)}\mathcal{N}(x_i|\mu_j^{(t)},\Sigma_j^{(t)})}. γik=p(zi=k∣xi,θ(t))=∑j=1Kπj(t)N(xi∣μj(t),Σj(t))πk(t)N(xi∣μk(t),Σk(t)).
- M 步 ：依据软分配更新参数
  π k ( t + 1 ) = 1 N ∑ i γ i k , μ k ( t + 1 ) = ∑ i γ i k x i ∑ i γ i k , Σ k ( t + 1 ) = ∑ i γ i k ( x i − μ k ( t + 1 ) ) ( x i − μ k ( t + 1 ) ) ⊤ ∑ i γ i k . \pi_k^{(t+1)}=\frac{1}{N}\sum_i\gamma_{ik},\quad \mu_k^{(t+1)}=\frac{\sum_i\gamma_{ik}x_i}{\sum_i\gamma_{ik}},\quad \Sigma_k^{(t+1)}=\frac{\sum_i\gamma_{ik}(x_i-\mu_k^{(t+1)})(x_i-\mu_k^{(t+1)})^\top}{\sum_i\gamma_{ik}}. πk(t+1)=N1i∑γik,μk(t+1)=∑iγik∑iγikxi,Σk(t+1)=∑iγik∑iγik(xi−μk(t+1))(xi−μk(t+1))⊤.
迭代直至对数似然收敛。
软聚类特性

与硬聚类（如 K‑Means）不同，GMM 为每个样本提供 属于每个簇的概率 ，能够处理 非球形、椭圆形 的簇结构，适用于 高维、复杂分布 的数据。

适用场景 :

场景	典型算法	说明
聚类	GMM + EM	需要捕捉簇的形状、大小不等或有重叠的情况（如图像分割、用户行为分群）[[5]]
密度估计	GMM	用于生成式模型、异常检测、概率预测等
隐马尔可夫模型（HMM）参数学习	EM（Baum‑Welch）	隐状态不可观测，使用 EM 迭代估计转移/发射概率[[6]]
混合朴素贝叶斯、因子分析等生成模型	EM	同样属于"隐变量"框架，EM 为通用求解器[[7]]
文本主题模型（LDA）	变分 EM / 采样 EM	隐主题是未标记的变量，使用 EM 近似求解

优点:

通用性强：只要模型可以写出完整数据的似然，就能套用 EM；对混合模型、隐马尔可夫模型、因子分析等均适用。
软分配：在 GMM 中提供每个样本的概率归属，能够表达不确定性，提升聚类质量。
单调收敛：每一步对数似然必不下降，保证算法的数值稳定性。
理论支撑：基于 Jensen 不等式的推导，使其在统计学上有严谨的证明

缺点与局限：

局部最优 ：EM 只保证收敛到 局部极大值，对多峰似然函数极易陷入次优解，需要多次随机初始化或使用模型选择技巧来缓解[[12]]。
计算成本 ：每次迭代都要计算所有样本对所有混合分量的后验概率，时间复杂度为 (O(NK D^2))（(D) 为特征维度），在大规模或高维数据上会显得昂贵[[13]]。
对初始值敏感 ：不同的初始均值、协方差或混合权重会导致截然不同的收敛结果，实际使用时常配合 K‑Means 或 层次聚类 进行预初始化
模型选择困难 ：需要手动指定混合分量数 K K K；若选错会导致欠拟合或过拟合。常用 BIC/AIC 、交叉验证或 非参数贝叶斯（如 Dirichlet Process GMM）来辅助选择
对噪声/离群点敏感 ：异常点会显著影响均值和协方差的估计，导致聚类质量下降；可通过 对角协方差 、稀疏协方差 或 鲁棒混合模型 进行改进

ref：常用聚类算法

mita大模型生成