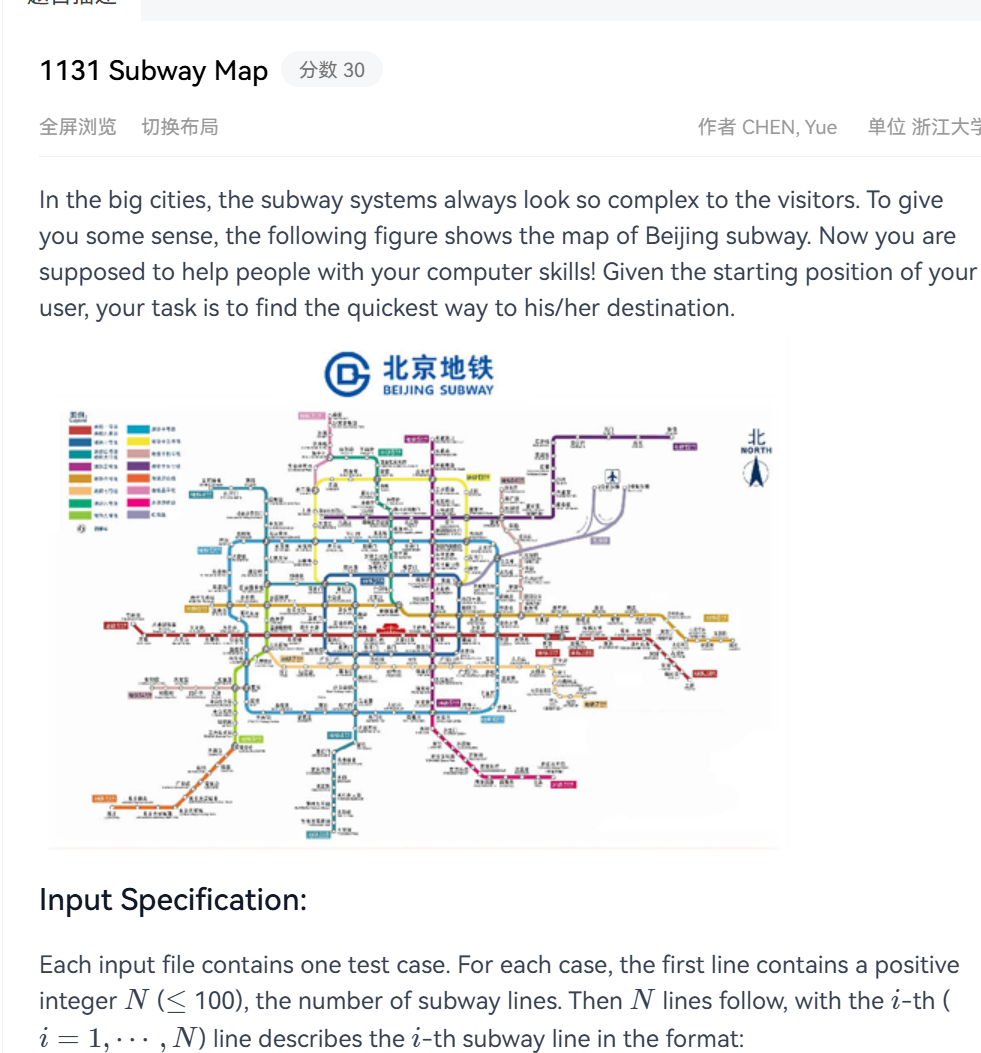


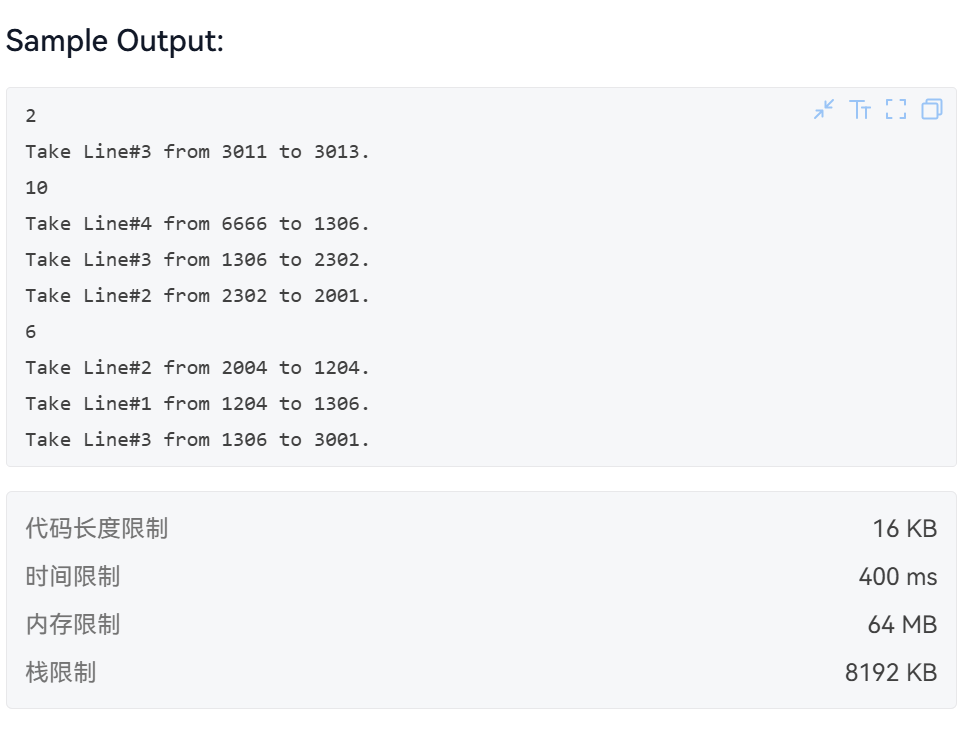
这一题的大意是给出了一个地铁站的线路图,让我们找从某一个站点出发到另外一个站点的最短距离,并且换乘次数最少。
找最短距离直接用dijkstra即可,是容易的,这一题的难点在于如何找最少的换乘次数,我刚开始用的是堆优化的dijkstra+dfs来找到每一条路径然后再从中找出最少的换乘次数,这样写很麻烦,我没有写出来如何找最少的换乘次数。
之后我借鉴了y总的思路,在建图的时候进行处理优化即可做出来。
如何进行优化呢?
我们知道这一题需要多次换乘,我们很难用代码来写某一站的时候确定换乘哪一个线路,因为一个站可以换乘多个线路。
我们可以选择在建图的时候多建些边,什么样呢?
原本:

现在:

我们在原来的基础上,对每一条线路,建任意两个站直达的边,这样我们就可以避免讨论换乘点了。
这一点是很巧妙的
剩下的就是用dijkstra来找最短路径了,需要注意的是在普通的堆优化的dijkstra的基础上增加了一个条件就是:
当最短路径相同时,优先通过站数少的,即有些最短路径可能相同,但可以直达的直接选择直达就好。
实际上这个条件就是让我们当在同一条路径上选择可以直达的(因为我们在建图的过程中,在每一条线路上都已经对每一个点都进行了建直达的边 )。
最后我们用一个字符串来保存在一条线路上的信息,把所有这样的信息放入字符串数组中最后输出结果即可。
完整代码如下:
cpp
#include <iostream>
#include <limits.h>
#include <cstring>
#include <queue>
#include <unordered_map>
#include <algorithm>
#include <cmath>
#include <vector>
#include <map>
using namespace std;
int N;
int M;
int head[10005];
int dist[10005];
bool flag[10005];
typedef pair<int,int> pii;
int cnt[10005];
priority_queue<pii,vector<pii>,greater<pii>> q;
struct node
{
int w;
int next;
int to;
int line;
}e[1000005];
int cut;
int pre[10005];
string info[10005];
void add(int x,int y,int w,int line)
{
e[cut].w=w;
e[cut].line=line;
e[cut].to=y;
e[cut].next=head[x];
head[x]=cut;
cut++;
}
string getnumber(int x)
{
string s=to_string(x);
while(s.size()<4)
{
s='0'+s;
}
return s;
}
void dijkstra(int s,int end)
{
memset(dist,0x3f,sizeof(dist));
memset(flag,0,sizeof(flag));
memset(cnt,0x3f,sizeof(cnt));
dist[s]=0;
cnt[s]=0;
q.push({dist[s],s});
while(!q.empty())
{
pii z=q.top();
q.pop();
int u=z.second;
if(flag[u]==0)
{
flag[u]=1;
for(int i=head[u];i!=-1;i=e[i].next)
{
int v=e[i].to;
if(flag[v]==0&&dist[v]>dist[u]+e[i].w)
{
dist[v]=dist[u]+e[i].w;
cnt[v]=cnt[u]+1;
pre[v]=u;
info[v]="Take Line#"+to_string(e[i].line)+" from "+getnumber(u)+" to "+getnumber(v)+".";
q.push({dist[v],v});
}
else if(dist[v]==dist[u]+e[i].w)
{
if(cnt[v]>cnt[u]+1)
{
cnt[v]=cnt[u]+1;
pre[v]=u;
info[v]="Take Line#"+to_string(e[i].line)+" from "+getnumber(u)+" to "+getnumber(v)+".";
}
}
}
}
else
{
continue;
}
}
cout<<dist[end]<<endl;
vector<string> ans;
for(int i=end;i!=s;i=pre[i])
{
ans.push_back(info[i]);
}
for(int i=ans.size()-1;i>=0;i--)
{
cout<<ans[i]<<endl;
}
}
int main()
{
//ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
cin>>N;
memset(head,-1,sizeof(head));
for(int i=0;i<N;i++)
{
cin>>M;
vector<int> stop;
for(int j=0;j<M;j++)
{
int x;
cin>>x;
stop.push_back(x);
}
for(int j=0;j<M;j++)
{
for(int k=0;k<j;k++)
{
//判断这两个点的距离也就是w这个权值
//注意可能有环,所以我们需要分情况讨论
int w= INT_MAX;
if(stop[0]==stop[M-1])
{
//有环
//找正反两条路的最小路
w=min(j-k,k-0+M-1-j);
}
else
{
//无环
w=j-k;
}
int line=i+1;
add(stop[k],stop[j],w,line);
add(stop[j],stop[k],w,line);
}
}
}
//这样就建好了图了
int m;
cin>>m;
for(int i=0;i<m;i++)
{
int start;
int end;
cin>>start>>end;
//cout<<"1"<<endl;
dijkstra(start,end);
}
return 0;
} 时间复杂度 点是10^4 边是10^6 ,边为什么是10^6呢 因为在一条线路上 原本能够建边的是10^2 ,又因为 在一条线路上任意两个点要建直达边, 故再乘上 10^2 ⇒ 10^4 ,而有N条路线 ,也即 10^4*10 ^ 2 ⇒ 10^6
dijkstra算法的时间复杂度大致为 O(10^6log10 ^ 4)⇒ k次询问 k=10 故总的时间复杂度为 10 ^ 7log10^4 是小于10^8的