【IQA技术专题】多维度注意力IQA：MANIQA

多维度注意力IQA：MANIQA（2022 CVPR）

• 专题介绍
• 一、研究背景
• 二、MANIQA方法
• • [2.1 Transposed Attention Block](#2.1 Transposed Attention Block)
  • [2.2 Scale Swin Transformer Block](#2.2 Scale Swin Transformer Block)
  • [2.3 Patch-weighted Quality Prediction](#2.3 Patch-weighted Quality Prediction)
• 三、实验
• 四、总结

本文将围绕《MANIQA: Multi-dimension Attention Network for No-Reference Image Quality Assessment》展开完整解析。

论文提出了多维度注意力网络（MANIQA） 用于无参考图像质量评估（NR-IQA），旨在解决现有方法在 GAN 生成失真图像上评估性能不足的问题。该模型以ViT 为特征提取器，通过转置注意力块（TAB） 增强通道间全局交互、尺度 Swin Transformer 块（SSTB） 强化斑块间局部交互，并采用斑块加权双分支预测结构输出最终质量分数。实验表明，MANIQA 在 LIVE、TID2013 等 4 个标准数据集上大幅超越现有最优方法，且在NTIRE 2022 NR-IQA 挑战赛中排名第一，展现出优异的泛化能力和对 GAN 失真图像的评估效果。参考资料如下：

1\]. [代码地址](https://github.com/IIGROUP/MANIQA) \[2\]. [论文地址](https://arxiv.org/abs/2204.08958) 论文整体结构思维导图如下：  *** ** * ** *** ## 专题介绍 图像质量评价（Image Quality Assessment, IQA）是图像处理、计算机视觉和多媒体通信等领域的关键技术之一。IQA不仅被用于学术研究，更在影像相关行业内实现了完整的商业化应用，涉及影视、智能手机、专业相机、安防监控、工业质检、医疗影像等。IQA与图像如影随形，其重要程度可见一斑。 但随着算法侧的能力不断突破，AIGC技术发展火热，早期的IQA或已无法准确评估新技术的能力。另一方面，千行百业中各类应用对图像质量的需求也存在差异和变化，旧标准也面临着适应性不足的挑战。 本专题旨在梳理和跟进IQA技术发展内容和趋势，为读者分享有价值、有意思的IQA。希望能够为底层视觉领域内的研究者和从业者提供一些参考和思路。 **系列文章如下：** 【1】🔥[IQA综述](https://blog.csdn.net/PixelMind/article/details/148371087) 【2】[PSNR\&SSIM](https://blog.csdn.net/PixelMind/article/details/147858875) 【3】[Q-Insight](https://blog.csdn.net/PixelMind/article/details/148935226) 【4】[VSI](https://blog.csdn.net/PixelMind/article/details/149152551) 【5】[LPIPS](https://blog.csdn.net/PixelMind/article/details/147992773) 【6】[DISTS](https://blog.csdn.net/PixelMind/article/details/148381735) 【7】[Q-align](https://blog.csdn.net/PixelMind/article/details/149183278) 【8】[GMSD](https://blog.csdn.net/PixelMind/article/details/149484709) 【9】[NIQE](https://blog.csdn.net/PixelMind/article/details/150401693) 【10】[MUSIQ](https://blog.csdn.net/PixelMind/article/details/150401665) 【11】[CDI](https://blog.csdn.net/PixelMind/article/details/150148000) 【12】[Q-BENCH](https://blog.csdn.net/PixelMind/article/details/154284846) 【13】[Q-Instruct](https://blog.csdn.net/PixelMind/article/details/154292308) 【14】[A-Fine](https://blog.csdn.net/PixelMind/article/details/154604419) *** ** * ** *** ## 一、研究背景 原始高质量图像在采集、压缩、传输及 GAN 修复过程中易失真，低质量图像会影响用户体验（如社交媒体）和关键系统运行（如自动驾驶），准确的感知质量评估具有重要实用价值。 现有方法局限有以下几个： 1. 传统 NR-IQA 方法分为基于自然场景统计（NSS）和深度学习两类，但前者难以建模真实世界复杂失真，后者在 GAN 生成失真图像上表现不足。 2. GAN 修复图像常含 "逼真但不真实" 的纹理，人类视觉系统（HVS）与机器视觉的认知差异导致现有模型评估不准确。 为此论文提出 MANIQA 模型，强化通道与空间维度的多尺度交互，提升对 GAN 失真图像的质量评估性能。 ## 二、MANIQA方法 论文整体结构如下所示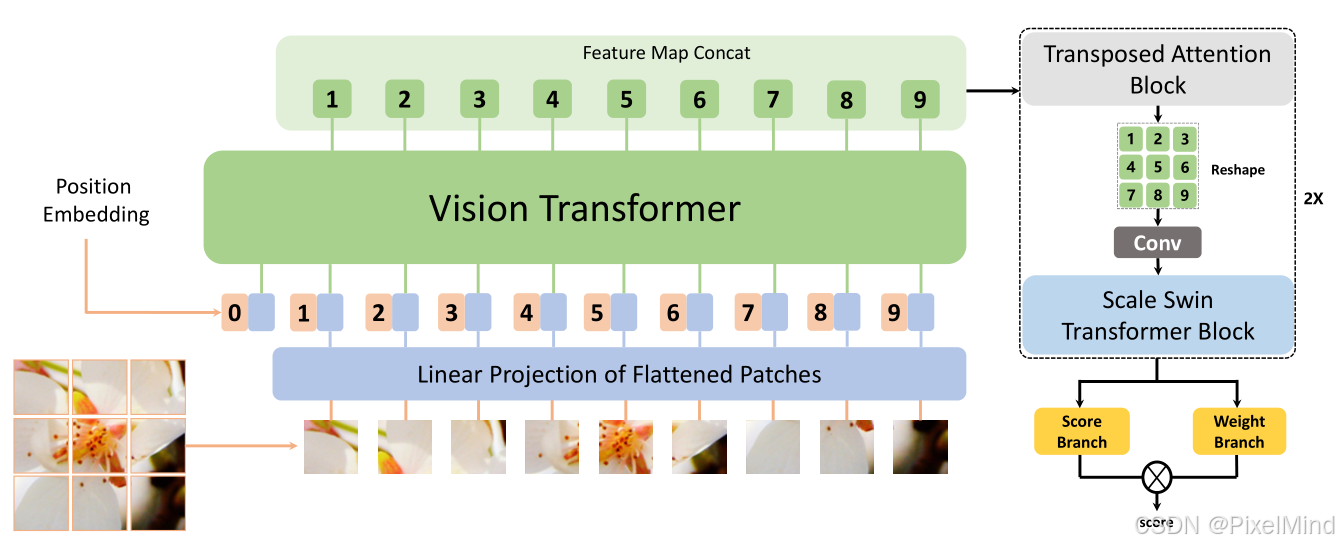：  大致的推理流程如下： 1. 输入图像分块与线性投影：首先follow VIT网络的结构，将图像划分为固定大小的不重叠斑块（Patch），以一个\[3, 224, 224\]的输入图像为例，patch_size设置为8的情况下，可得到(224/8)×(224/8)=28×28=784个patch，每个patch的维度是3*8* 8=768，会经过一个线性投影，得到斑块特征序列，Shape 为 \[784, 768\]，对应于图中的Linear Projection of Flattened Patches，公式如下所示： x p = Linear ( Flatten ( I p ) ) , p = 1 , 2 , ... , N \\bm{x}_p = \\text{Linear}(\\text{Flatten}(\\bm{I}_p)), \\quad p = 1,2,\\dots,N xp=Linear(Flatten(Ip)),p=1,2,...,N其中： I p ∈ R 3 × 8 × 8 \\bm{I}_p \\in \\mathbb{R}\^{3 \\times 8 \\times 8} Ip∈R3×8×8 为第 p p p 个图像斑块， N = ( H / 8 ) × ( W / 8 ) N = (H/8) \\times (W/8) N=(H/8)×(W/8) 为总斑块数（输入 224 × 224 224 \\times 224 224×224 时 N = 784 N=784 N=784）， x p ∈ R D \\bm{x}_p \\in \\mathbb{R}\^{D} xp∈RD 为投影后的斑块特征（ D = 768 D=768 D=768 对应 ViT-B/8）， Flatten ( ⋅ ) \\text{Flatten}(\\cdot) Flatten(⋅) 为展平操作， Linear ( ⋅ ) \\text{Linear}(\\cdot) Linear(⋅) 为线性层。 后续需要加入一个位置嵌入（Position Embedding）（Shape：\[1, 768\]），最终输入 ViT 的特征序列 Shape 为 \[785, 768\]（784 个斑块 + 1 个位置嵌入），0号通常是用于分类的token，这个过程在[MUSIQ](https://blog.csdn.net/PixelMind/article/details/150401665)中有讲解。公式如下所示： X in = \[ x cls ; x 1 , x 2 , ... , x N \] ∈ R ( N + 1 ) × D \\bm{X}_{\\text{in}} = \\left\[ \\bm{x}_{\\text{cls}}; \\bm{x}_1, \\bm{x}_2, \\dots, \\bm{x}_N \\right\] \\in \\mathbb{R}\^{(N+1) \\times D} Xin=\[xcls;x1,x2,...,xN\]∈R(N+1)×D其中 x cls ∈ R 1 × D \\bm{x}_{\\text{cls}} \\in \\mathbb{R}\^{1 \\times D} xcls∈R1×D 为类别嵌入（位置嵌入）。 2. ViT 特征提取与多特征拼接：将上述特征序列输入 Vision Transformer（ViT-B/8），经过 12 层 Transformer Block 的计算后，输出各层的特征图，选取 ViT 的第 7\~10 层输出特征（共 4 层），将这些层的斑块特征（排除位置嵌入）进行拼接，单一层的斑块特征 Shape：\[784, 768\]，拼接后 Shape：\[784, 768×4\] = \[784, 3072\]。公式如下所示： X concat = Concat ( X 7 , X 8 , X 9 , X 10 ) ∈ R N × 4 D \\bm{X}_{\\text{concat}} = \\text{Concat}\\left( \\bm{X}_7, \\bm{X}_8, \\bm{X}_9, \\bm{X}_{10} \\right) \\in \\mathbb{R}\^{N \\times 4D} Xconcat=Concat(X7,X8,X9,X10)∈RN×4D其中 X l ∈ R N × D \\bm{X}_l \\in \\mathbb{R}\^{N \\times D} Xl∈RN×D 为 ViT 第 l l l 层的斑块特征（剔除 x cls \\bm{x}_{\\text{cls}} xcls）， Concat ( ⋅ ) \\text{Concat}(\\cdot) Concat(⋅) 为通道维度拼接操作， 4 D = 3072 4D=3072 4D=3072。 3. 转置注意力块（Transposed Attention Block）的通道全局交互：在通道维度上执行自注意力机制（TAB 的核心），建模不同通道间的全局依赖关系，Reshape成原始空间的形状，最后通过 1×1 卷积层将通道数从 3072 压缩至 768，输出 Shape 为 \[768, 28, 28\]。 4. 尺度 Swin Transformer 块（Scale Swin Transformer Block）的空间局部交互：将 TAB 输出的特征图（Shape：\[768, 28, 28\]）输入SSTB，在空间维度上执行局部窗口注意力（窗口大小通常为 4×4），同时引入 "尺度因子 α" 稳定训练，增强斑块间的局部交互。SSTB 输出的特征图 Shape 仍为 \[768, 28, 28\]（空间维度保持 28×28，通道维度 768）。 5. 双分支预测与分数融合：权重分支（Weight Branch）：将 SSTB 输出的特征图通过全连接层，预测每个斑块的 "重要性权重"，Shape 为 \[784, 1\]（784 个斑块，每个对应 1 个权重值）。分数分支（Score Branch）：同理，通过另一个全连接层预测每个斑块的 "质量分数"，Shape 为 \[784, 1\]。将权重分支与分数分支的输出进行逐元素相乘（哈达玛积），得到每个斑块的 "加权质量分数"，再对所有斑块的分数求和，最终输出整个图像的质量分数（标量）。 接下来将分模块进行讲解。 ### 2.1 Transposed Attention Block 如下图所示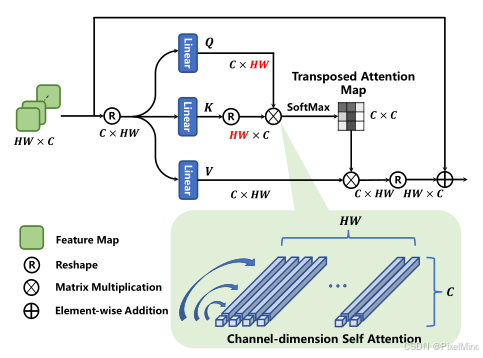：  它的计算过程可以用下式表示： F reshape = Reshape ( X concat ) ∈ R 4 D × H p × W p \\bm{F}_{\\text{reshape}} = \\text{Reshape}(\\bm{X}_{\\text{concat}}) \\in \\mathbb{R}\^{4D \\times H_p \\times W_p} Freshape=Reshape(Xconcat)∈R4D×Hp×Wp A ch = Softmax ( F reshape ⋅ F reshape ⊤ 4 D ) ∈ R 4 D × 4 D \\bm{A}_{\\text{ch}} = \\text{Softmax}\\left( \\frac{\\bm{F}_{\\text{reshape}} \\cdot \\bm{F}_{\\text{reshape}}\^\\top}{\\sqrt{4D}} \\right) \\in \\mathbb{R}\^{4D \\times 4D} Ach=Softmax(4D Freshape⋅Freshape⊤)∈R4D×4D F tab = A ch ⋅ F reshape ∈ R 4 D × H p × W p \\bm{F}_{\\text{tab}} = \\bm{A}_{\\text{ch}} \\cdot \\bm{F}_{\\text{reshape}} \\in \\mathbb{R}\^{4D \\times H_p \\times W_p} Ftab=Ach⋅Freshape∈R4D×Hp×Wp 其中 H p = W p = 28 H_p = W_p = 28 Hp=Wp=28（对应 224 / 8 224/8 224/8) ， ⋅ \\cdot ⋅ 为矩阵乘法， 4 D \\sqrt{4D} 4D 为缩放因子， Softmax ( ⋅ ) \\text{Softmax}(\\cdot) Softmax(⋅) 沿行维度计算， Conv 1 × 1 ( ⋅ ) \\text{Conv}_{1 \\times 1}(\\cdot) Conv1×1(⋅) 为 1×1 卷积，将通道数从 4 D 4D 4D 降至 D = 768 D=768 D=768。对照计算公式，我们可以发现它就是一个通道级别的自注意力机制，相当空间注意力计算量要小很多。 另外经过Transposed Attention Block处理后的特征还需要降维，用下式表示： F tab降维 = Conv 1 × 1 ( F tab ) ∈ R D × H p × W p \\bm{F}_{\\text{tab降维}} = \\text{Conv}_{1 \\times 1}(\\bm{F}_{\\text{tab}}) \\in \\mathbb{R}\^{D \\times H_p \\times W_p} Ftab降维=Conv1×1(Ftab)∈RD×Hp×Wp其中 Conv 1 × 1 ( ⋅ ) \\text{Conv}_{1 \\times 1}(\\cdot) Conv1×1(⋅) 为 1×1 卷积，将通道数从 4 D 4D 4D 降至 D = 768 D=768 D=768。 ### 2.2 Scale Swin Transformer Block 结构如下所示，SSTB的输入是降维后的输出结果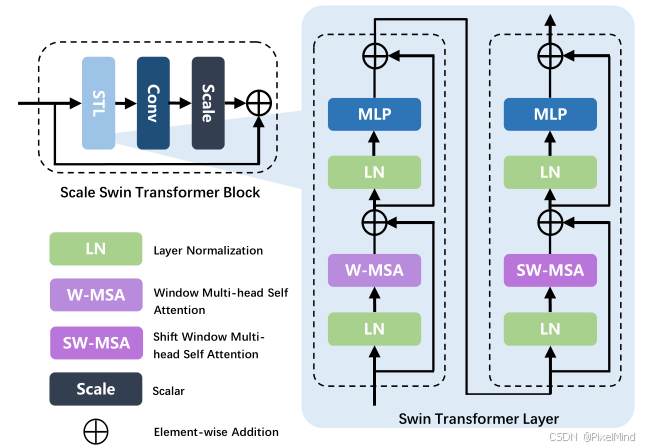：  计算过程如下式所示： F sstb = F tab降维 + α ⋅ SwinBlock ( F tab降维 ) \\bm{F}_{\\text{sstb}} = \\bm{F}_{\\text{tab降维}} + \\alpha \\cdot \\text{SwinBlock}(\\bm{F}_{\\text{tab降维}}) Fsstb=Ftab降维+α⋅SwinBlock(Ftab降维)其中 α ∈ \[ 0.1 , 0.2 \] \\alpha \\in \[0.1, 0.2\] α∈\[0.1,0.2\] 为尺度因子（实验最优值 0.1）， SwinBlock ( ⋅ ) \\text{SwinBlock}(\\cdot) SwinBlock(⋅) 为 Swin Transformer 基础块（含窗口注意力、MLP），输出 F sstb ∈ R D × H p × W p \\bm{F}_{\\text{sstb}} \\in \\mathbb{R}\^{D \\times H_p \\times W_p} Fsstb∈RD×Hp×Wp。其中STL的计算过程如右图所示：使用了Swin transformer中的window-MSA和shift window-MSA。 可以发现，相比较原始的swin块，添加了scale来控制STL的输出，作者认为其可以稳定训练过程且增强平移等变性。 ### 2.3 Patch-weighted Quality Prediction 结构如下所示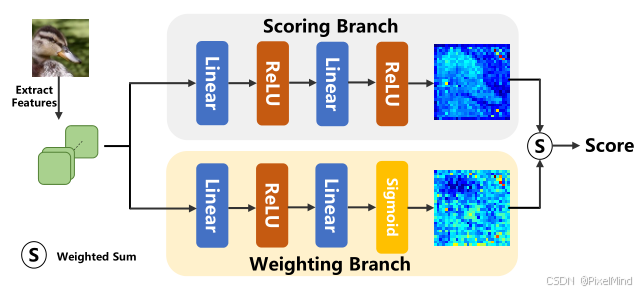：  公式表示如下： W = FC 1 ( Flatten ( F sstb ) ) ∈ R N × 1 \\bm{W} = \\text{FC}_1\\left( \\text{Flatten}(\\bm{F}_{\\text{sstb}}) \\right) \\in \\mathbb{R}\^{N \\times 1} W=FC1(Flatten(Fsstb))∈RN×1 S = FC 2 ( Flatten ( F sstb ) ) ∈ R N × 1 \\bm{S} = \\text{FC}_2\\left( \\text{Flatten}(\\bm{F}_{\\text{sstb}}) \\right) \\in \\mathbb{R}\^{N \\times 1} S=FC2(Flatten(Fsstb))∈RN×1 S weighted = W ⊙ S ∈ R N × 1 \\bm{S}_{\\text{weighted}} = \\bm{W} \\odot \\bm{S} \\in \\mathbb{R}\^{N \\times 1} Sweighted=W⊙S∈RN×1其中 FC 1 ( ⋅ ) \\text{FC}_1(\\cdot) FC1(⋅) 为全连接层（输出维度 1）， W \\bm{W} W 为每个斑块的重要性权重。 FC 2 ( ⋅ ) \\text{FC}_2(\\cdot) FC2(⋅) 为另一全连接层， S \\bm{S} S 为每个斑块的质量分数。 ⊙ \\odot ⊙ 为哈达玛积（逐元素相乘）。 可见预测分数前会有两个独立分支，对每个patch进行weight和分数的独立预测，最后再将他们合并，相当于给他们的分数分配重要性权重。 最终的分数计算得来， Q = 1 N ∑ p = 1 N S weighted , p Q = \\frac{1}{N} \\sum_{p=1}\^N \\bm{S}_{\\text{weighted}, p} Q=N1p=1∑NSweighted,p其中 S weighted , p \\bm{S}_{\\text{weighted}, p} Sweighted,p 为第 p p p 个斑块的加权分数， Q ∈ \[ 0 , 1 \] Q \\in \[0, 1\] Q∈\[0,1\] 为最终质量分数（越高表示图像质量越好）。 损失函数作者采用了MSE的损失，公式如下： L = 1 B ∑ i = 1 B ( Q i − Q \^ i ) 2 \\mathcal{L} = \\frac{1}{B} \\sum_{i=1}\^B (Q_i - \\hat{Q}_i)\^2 L=B1i=1∑B(Qi−Q\^i)2其中 B B B 为批次大小， Q i Q_i Qi 为模型预测分数， Q \^ i \\hat{Q}_i Q\^i 为人类主观评分（归一化至 \[ 0 , 1 \] \[0,1\] \[0,1\]）。 ## 三、实验 **定量实验**如下所示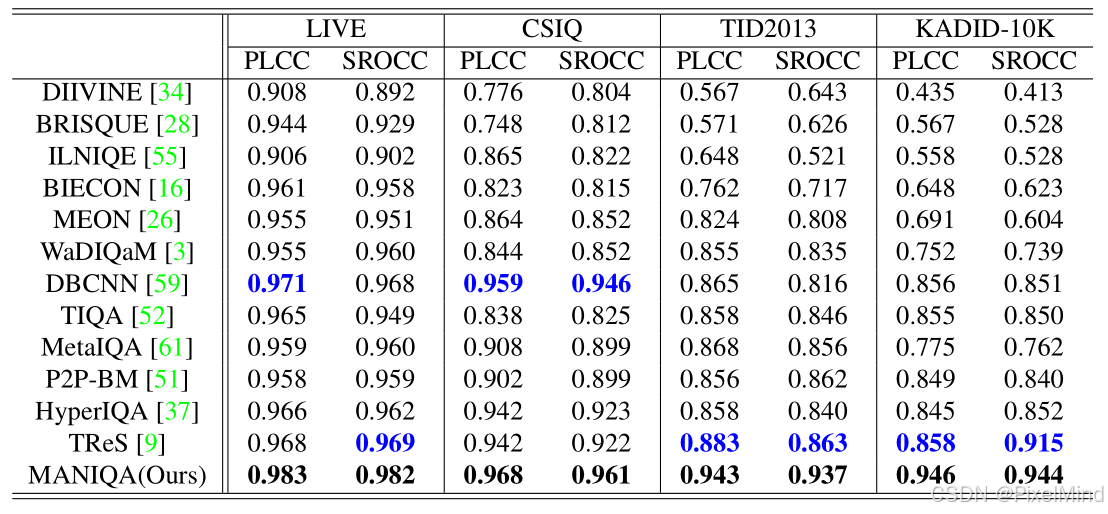：  MANIQA 在传统失真数据集上的预测结果与人类主观评分一致性显著高于现有方法。KADID这类大规模多样化失真数据集上，MANIQA 的性能优势进一步扩大（PLCC 提升 0.088）。 在NTIRE比赛上的实验如下。 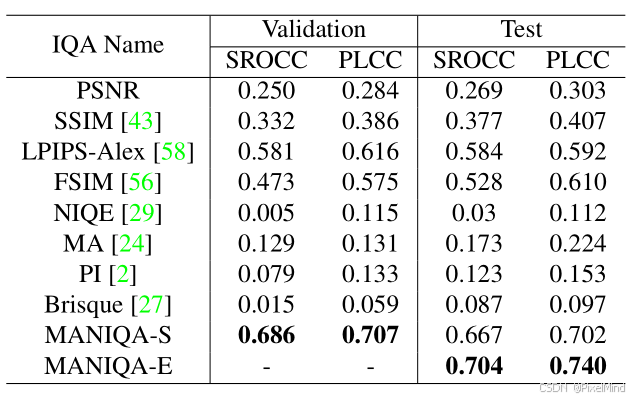 MANIQA-S（单模型）已达到挑战赛领先水平，验证了 MANIQA 对 GAN 失真图像的评估能力。MANIQA-E（集成模型）在挑战赛中排名第一，是当前 GAN 失真图像质量评估的最优方法之一。 **消融实验**如下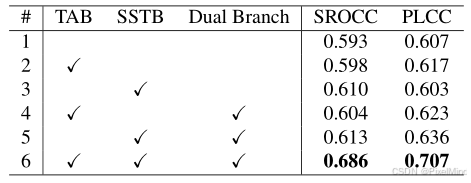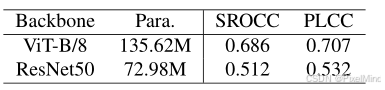：   可以得到以下结论： 1. 无 TAB + 无 SSTB + 单分支：多维度注意力（TAB+SSTB）和双分支结构是性能提升的核心模块。 2. 有 TAB + 无 SSTB + 单分支：转置注意力块（TAB）有效增强了通道全局交互，SROCC/PLCC 各提升 0.05。 3. 有 TAB + 有 SSTB + 单分支 ：尺度 Swin 块（SSTB）进一步强化空间局部交互，SROCC 再提升 0.017。 4. 有 TAB + 有 SSTB + 双分支：双分支加权融合平衡了显著区域与高质量区域，PLCC 提升 0.023。 5. ResNet50 骨干（替代 ViT）：ViT 的长距离依赖建模能力远优于 CNN，是 MANIQA 高性能的基础，对应于第2个表格。 另外两个是关于权重图和预测结果的定性实验图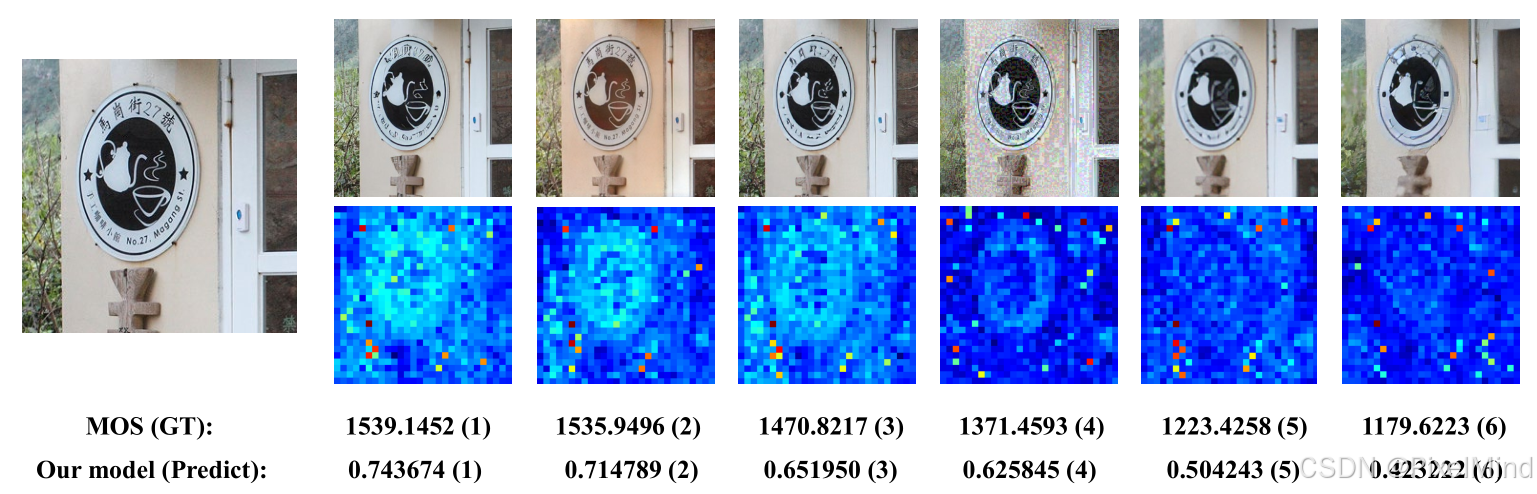：  左侧是原始质量图像，右侧是失真图像。MOS 代表真实的人类主观评分。括号中的数字表示该失真图像在本图所有失真图像中的排名。失真图像下方是斑块权重图。可以看到MANIQA跟人类的打分很接近，且对于正常的图像，权重图会集中于质量高的区域，否则会较为平均。 下图作者用了一些图像分析了输出的两个分支结果，这些结果都存在gan的瑕疵纹理：  可以看到，斑块权重图聚焦于人类视觉中值得关注的显著目标区域，而斑块分数图更关注视觉体验更佳的区域。当人类观察一幅图像时，正是图像中的主体本身极大地影响着我们的感知。因此，这些区域在图中被赋予了较高的权重。然而，高质量区域并不总是位于这些包含重要语义信息的区域中。由于显著区域与高质量区域存在不一致性，最终加权图需同时依赖斑块权重图和分数图来生成。我们认为，双分支结构能够抑制高权重斑块的过度影响，从而降低模型过拟合的风险。 ## 四、总结 文章引入多维度（通道全局 + 空间局部）注意力交互能有效提升 NR-IQA 性能，尤其适用于 GAN 失真图像的评估。未来的优化方向可能是细分 GAN 失真类型（如愉悦虚假纹理、不愉悦虚假纹理），进一步优化模型对特定失真的适应性。 *** ** * ** *** **感谢阅读，欢迎留言或私信，一起探讨和交流，如果对你有帮助的话，也希望可以给博主点一个关注，谢谢。**