文章目录
- 前言
- 一.开放定址法概念
- 二.开放定址法的基本原理
- 三.线性探测法(插入、查找操作)
- 四.平方探测法(插入、查找操作)
- 五.双散列法(插入、查找操作)
- 六.伪随机序列法(插入、查找操作)
- 七.删除元素
- 八.知识回顾与重要考点
- 九.拓展:"探测覆盖率"
- 结论
前言
摘要:本文系统介绍了开放定址法的四种常用冲突处理方法。开放定址法通过探测序列(线性探测、平方探测、双散列、伪随机序列)为冲突元素寻找空闲位置。文中详细阐述了每种方法的原理、公式及操作步骤,并通过具体示例演示了插入、查找和删除过程。特别强调删除操作需采用逻辑删除标记,避免截断探测路径。这些方法在处理散列表冲突时各具特点,为数据存储和检索提供了有效解决方案.
一.开放定址法概念
- 开放定址法:如果发生"冲突",就给新元素找另一个空闲位置。
- 例:某散列表的长度为13,散列函数 H(key)=key%13。依次将数据元素 19、14、23、1 插入散列表

- 2这个地址既可以用于存储这个地址所对应的同义词,也可以用于存储这个地址的非同义词
为什么叫"开放定址"?------一个散列地址,既对同义词开放,也对非同义词开放。
二.开放定址法的基本原理
1.基本原理
- 当这个初始散列地址发生冲突的时候,我们需要设计一个探测序列去寻找下一个空闲的位置
2.公式
- 发生第i次冲突时的散列地址( H i H_i Hi): H i = ( H ( k e y ) + d i ) % m Hi=(H(key)+di)\%m Hi=(H(key)+di)%m
其中 H ( k e y ) H(key) H(key)表示初始散列地址, d i d_i di表示探测序列的第i个偏移量,m表示散列表的表长
3.四种常用方法构造探测序列 d i d_i di
1.内容
- 线性探测法(探测序列/增量序列) d i = 0 , 1 , 2 , 3 , ... , m − 1 d_{i}=0,1,2,3,...,m-1 di=0,1,2,3,...,m−1
- 平方探测法(二次探测法) d i = 0 2 , 1 2 , − 1 2 , 2 2 , − 2 2 , ... , k 2 , − k 2 。其中 k ≤ m / 2 d_{i}=0^{2},1^{2},-1^{2},2^{2},-2^{2},\dotsc ,k^{2},-k^{2}。其中k≤m/2 di=02,12,−12,22,−22,...,k2,−k2。其中k≤m/2
- 双散列法 d 1 = i ✖ ® h a s h 2 ( k e y ) 。其中 h a s h 2 ( k e y ) 是另一散列函数 d_{1}=i✖️hash_{2}(key)。其中 hash_{2}(key) 是另一散列函数 d1=i✖R◯hash2(key)。其中hash2(key)是另一散列函数
- 伪随机序列法 d i 是一个伪随机序列,如 d = 0 , 5 , 3 , 11 , . . . d_{i}是一个伪随机序列,如d=0,5,3,11,... di是一个伪随机序列,如d=0,5,3,11,...
2.区别与联系
- 每一个探测序列的 d 0 d_0 d0这个元素都等于0
- 每一个探测序列的下标i最大值不超过m-1,因为散列表的总长只有m,因此当我们的探测范围就是0~m-1
三.线性探测法(插入、查找操作)
1.具体例子
- 例:长度为13的散列表状态如下图所示,散列函数 H ( K e y ) = k e y % 13 H(Key)=key\% 13 H(Key)=key%13,采用线性探测法解决冲突。分析:插入元素1、查找元素1的过程
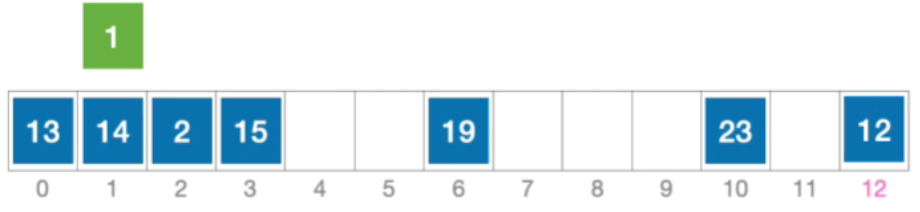
- 初始散列地址H₀=1%13=1,发生冲突(第1次),那这就是他的初始散列地址显然发生了冲突
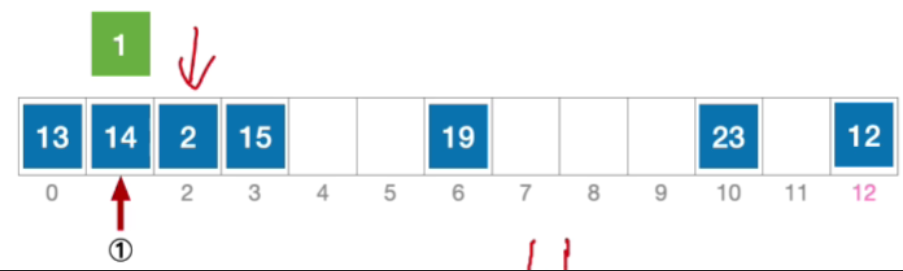
- 由于采用了线性探测法,所以初始的这个位置发生冲突之后应该探测初始位置往右偏移一个单位
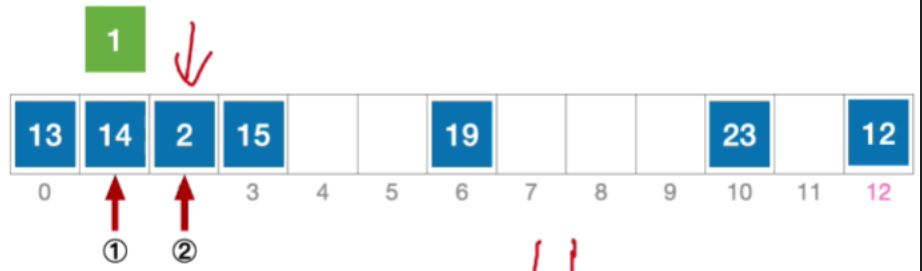
- 这个位置依然冲突,接下来应该探测初始地址加2,也就是3
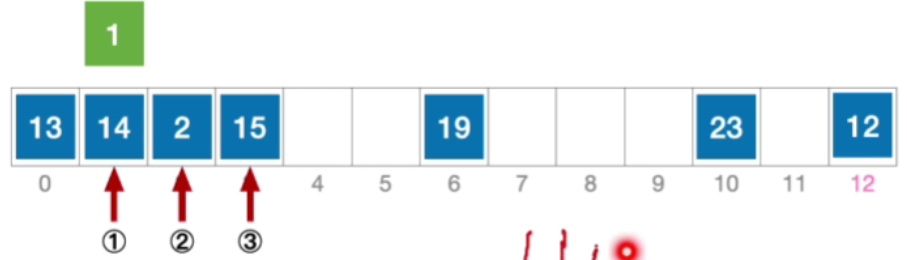
- 这个地址依然冲突,所以接下来应该探测初始地址加3,也就是4
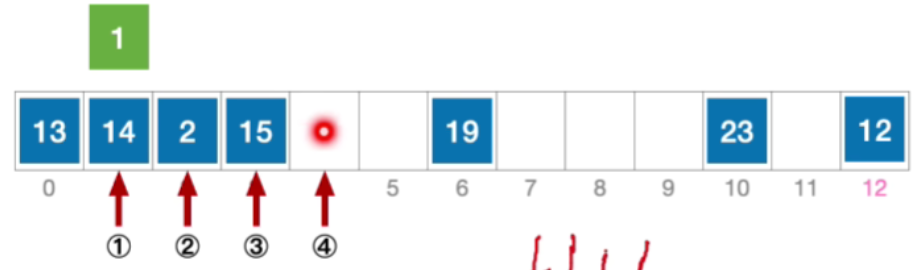
- 这个地址没有发生冲突,那我们就可以把元素1插入到这个位置
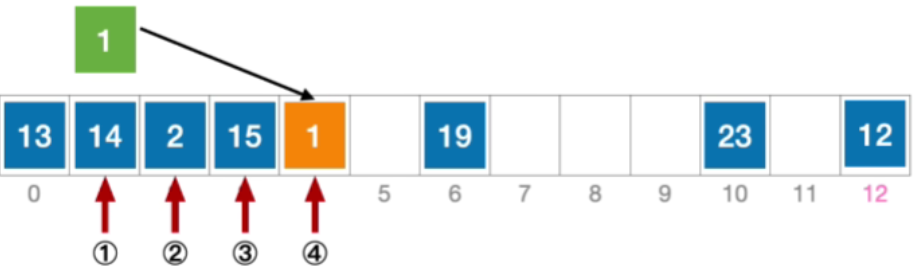
- 公式化描述: 初始散列地址 H 0 = 1 % 13 = 1 , 发生冲突(第 1 次) H 1 = ( 1 + 1 ) % 13 = 2 ,发生冲突(第 2 次) H 2 = ( 1 + 2 ) % 13 = 3 ,发生冲突(第 3 次) H 3 = ( 1 + 3 ) % 13 = 4 ,未发生冲突,插入位置# 4 \begin{aligned}&初始散列地址 H_{0}=1\% 13=1,发生冲突(第1次)\\ &H_{1}=(1+1)\%13=2,发生冲突(第2次)\\ &H_{2}=(1+2)\%13=3,发生冲突(第3次)\\ &H_{3}=(1+3)\%13=4,未发生冲突,插入位置 \text{\#}4\end{aligned} 初始散列地址H0=1%13=1,发生冲突(第1次)H1=(1+1)%13=2,发生冲突(第2次)H2=(1+2)%13=3,发生冲突(第3次)H3=(1+3)%13=4,未发生冲突,插入位置#4
注:查找操作原理类似,根据探测序列依次对比各存储单元内的关键字。
若探测到目标关键字,则查找成功。
若探测到空单元,则查找失败。
四.平方探测法(插入、查找操作)
1.具体例子
- 例:长度为13的散列表状态如下图所示,散列函数H(Key)=key%13,采用平方探测法解决冲突。分析:插入元素1、查找元素1的过程
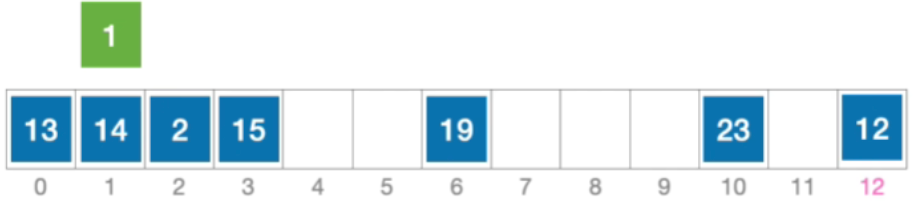
- 初始散列地址H₀=1%13=1,发生冲突(第1次)
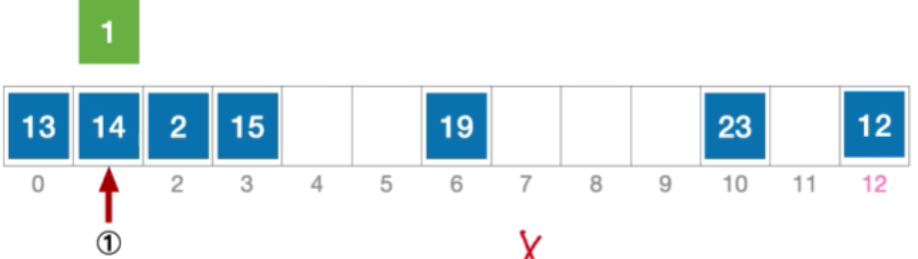
- 接下来探测初始地址加 1 2 1^2 12的位置,也就是2,依然冲突
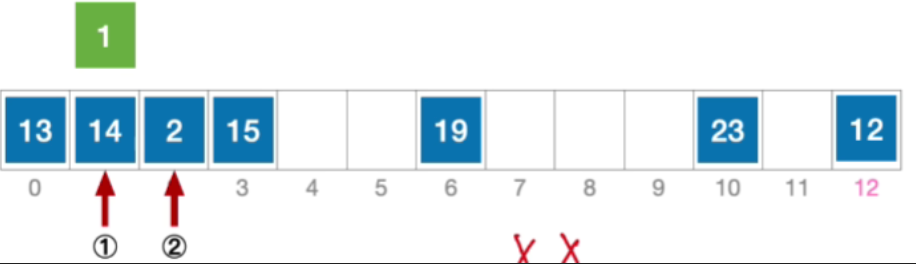
- 接下来探测初始地址加 − 1 2 -1^2 −12的位置,也就是0,依然冲突
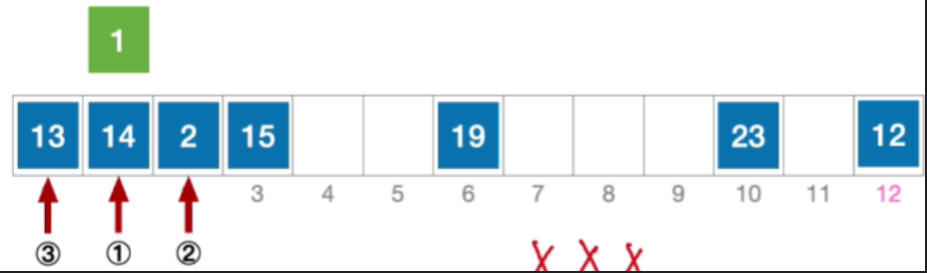
- 接下来探测初始地址加 2 2 2^2 22的位置,也就是5,没有冲突
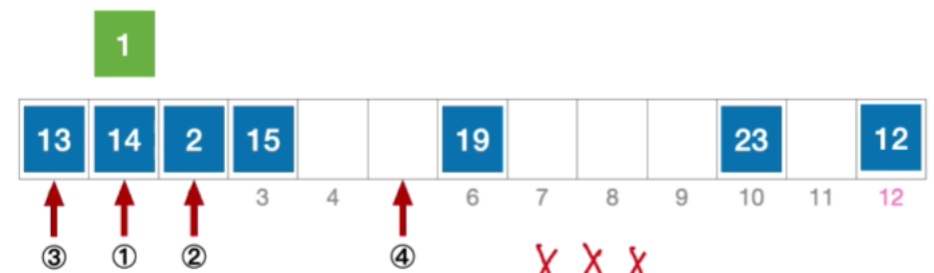
- 插入元素1
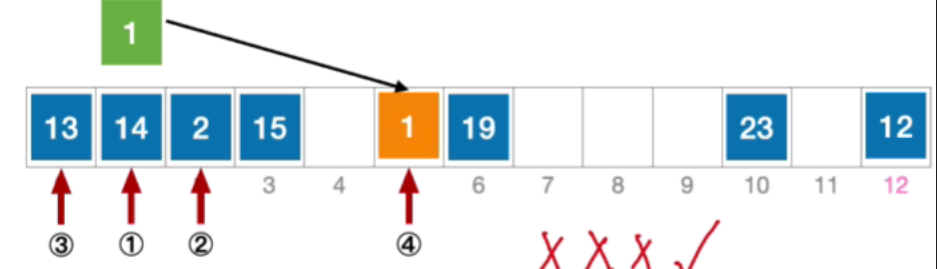
- 公式化描述 初始散列地址 H 0 = 1 % 13 = 1 , 发生冲突(第 1 次) H 1 = ( 1 + 1 2 ) % 13 = 2 ,发生冲突(第 2 次) H 2 = ( 1 + − 1 2 ) % 13 = 0 ,发生冲突(第 3 次) H 3 = ( 1 + 2 2 ) % 13 = 5 ,未发生冲突,插入位置# 5 \begin{aligned}&初始散列地址 H_{0}=1\% 13=1,发生冲突(第1次)\\ &H_{1}=(1+1^2)\%13=2,发生冲突(第2次)\\ &H_{2}=(1+-1^2)\%13=0,发生冲突(第3次)\\ &H_{3}=(1+2^2)\%13=5,未发生冲突,插入位置 \text{\#}5\end{aligned} 初始散列地址H0=1%13=1,发生冲突(第1次)H1=(1+12)%13=2,发生冲突(第2次)H2=(1+−12)%13=0,发生冲突(第3次)H3=(1+22)%13=5,未发生冲突,插入位置#5
注:查找操作原理类似,根据探测序列依次对比各存储单元内的关键字。
若探测到目标关键字,则查找成功。
若探测到空单元,则查找失败。
五.双散列法(插入、查找操作)
- 例:长度为13的散列表状态如下图所示,散列函数H(key)=key% 13,采用双散列法解决冲突,假设hash_{2}(key)=13-(key% 13)。分析:插入元素1、查找元素1的过程
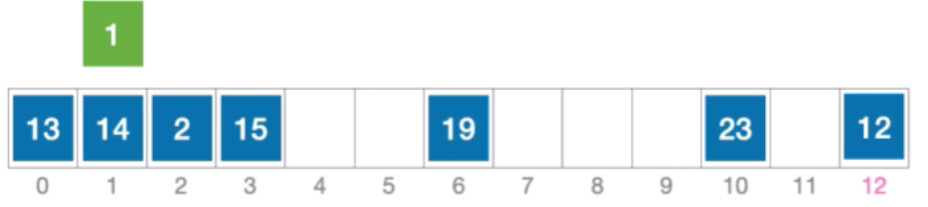
- 初始散列地址H₀=1%13=1,发生冲突(第1次),发生冲突
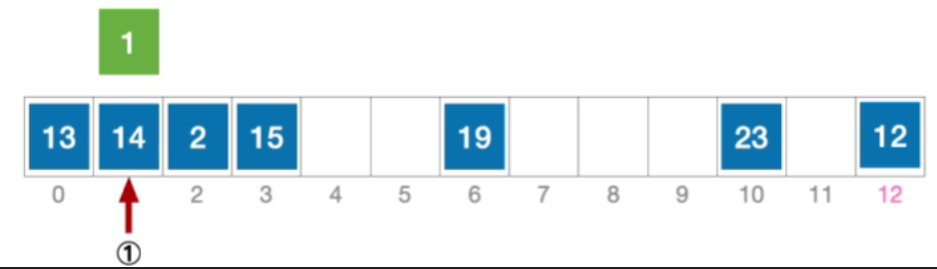
- 那发生冲突之后,后一个地址的确定取决于第二个散列函数,算出来的值 h a s h 2 ( k e y ) = 13 − ( k e y % 13 ) = 12 hash_2(key)=13-(key\%13)=12 hash2(key)=13−(key%13)=12,所以 H 1 = ( 1 + 1 ∗ 12 ) % 13 = 0 ,发生冲突(第 2 次) H_{1}=(1+1*12)\%13=0,发生冲突(第2次) H1=(1+1∗12)%13=0,发生冲突(第2次)
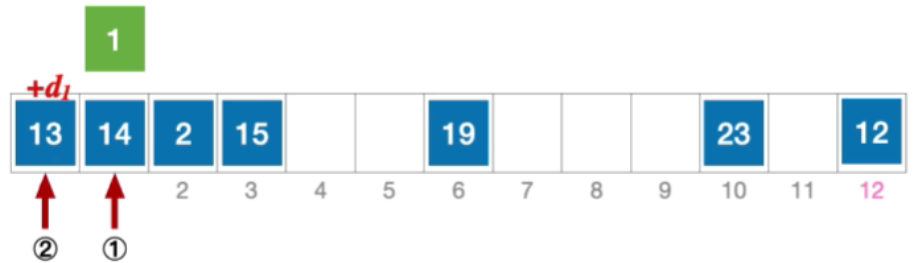
- 所以计算后一个应该探测的位置, H 2 = ( 1 + 2 ∗ 12 ) % 13 = 12 ,发生冲突 ( 第 3 次 ) H_{2}=(1+2*12)\% 13=12,发生冲突(第3次) H2=(1+2∗12)%13=12,发生冲突(第3次)
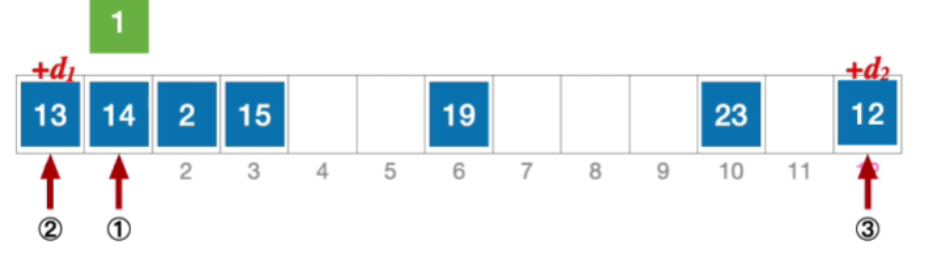
- H 3 = ( 1 + 3 ∗ 12 ) % 13 = 11 , 未发生冲突,插入位置 # 11 H_{3}=(1+3*12)\% 13=11,未发生冲突,插入位置\#11 H3=(1+3∗12)%13=11,未发生冲突,插入位置#11
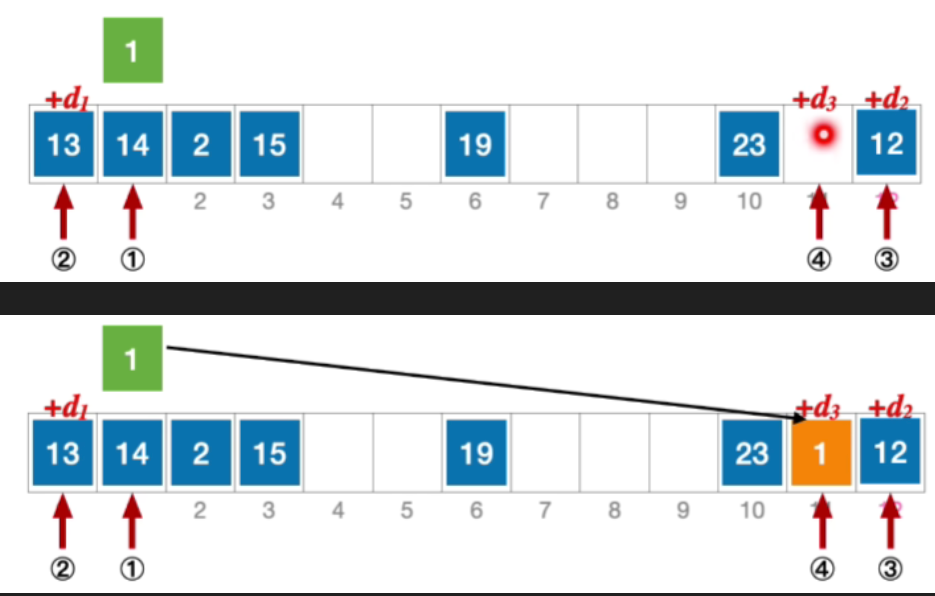
- 公式化描述 初始散列地址 H 0 = 1 % 13 = 1 , 发生冲突(第 1 次) 由于 k e y = 1 , h a s h 2 ( k e y ) = 13 − ( k e y % 13 ) = 12 H 1 = ( 1 + 12 ) % 13 = 0 ,发生冲突(第 2 次) H 2 = ( 1 + 12 ) % 13 = 12 ,发生冲突(第 3 次) H 3 = ( 1 + 12 ) % 13 = 11 ,未发生冲突,插入位置# 11 \begin{aligned}&初始散列地址 H_{0}=1\% 13=1,发生冲突(第1次)\\ &由于key=1,hash2(key)=13-(key\%13)=12\\&H_{1}=(1+12)\%13=0,发生冲突(第2次)\\ &H_{2}=(1+12)\%13=12,发生冲突(第3次)\\ &H_{3}=(1+12)\%13=11,未发生冲突,插入位置 \text{\#}11\end{aligned} 初始散列地址H0=1%13=1,发生冲突(第1次)由于key=1,hash2(key)=13−(key%13)=12H1=(1+12)%13=0,发生冲突(第2次)H2=(1+12)%13=12,发生冲突(第3次)H3=(1+12)%13=11,未发生冲突,插入位置#11
注:查找操作原理类似,根据探测序列依次对比各存储单元内的关键字。
若探测到目标关键字,则查找成功。
若探测到空单元,则查找失败。
六.伪随机序列法(插入、查找操作)
- 例:长度为13的散列表状态如下图所示,散列函数H(Key)=key%13,采用伪随机序列法解决冲突,假设伪随机序列 d i = 0 , 5 , 3 , 11 , ... d_{i}=0,5,3,11,\dotsc di=0,5,3,11,...,其中d_{i}表示第i次发生冲突时的增量。分析:插入元素1、查找元素1的过程
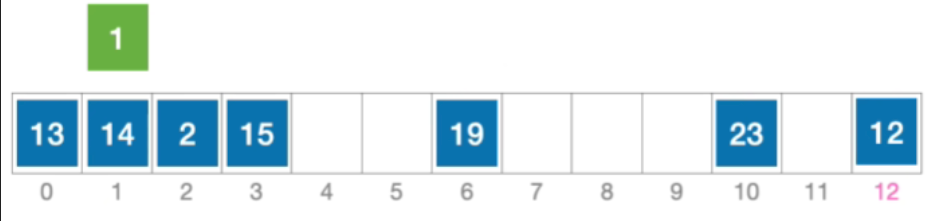
- 初始散列地址H₀=1%13=1,发生冲突(第1次)
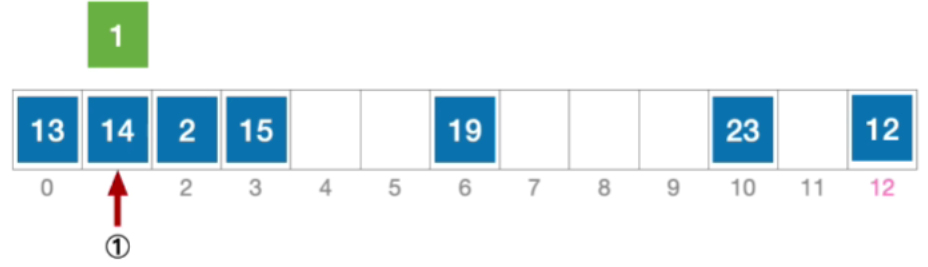
- 接下来应该探测往右偏移5个单位的位置,也就是6,发生冲突
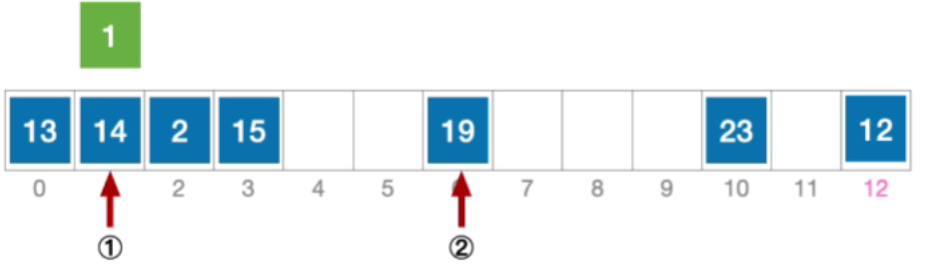
- 接下来应该探测往右偏移3的位置,也就是4,发现是空,因此插入1
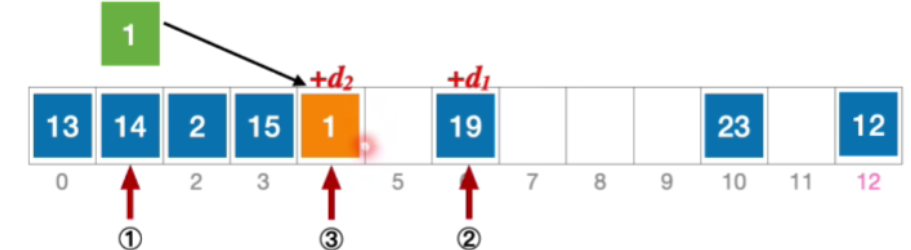
- 表达式描述 初始散列地址 H 0 = 1 % 13 = 1 , 发生冲突(第 1 次) H 1 = ( 1 + 5 ) % 13 = 6 ,发生冲突(第 2 次) H 2 = ( 1 + 3 ) % 13 = 4 ,未发生冲突,插入位置# 4 \begin{aligned}&初始散列地址 H_{0}=1\% 13=1,发生冲突(第1次)\\ &H_{1}=(1+5)\%13=6,发生冲突(第2次)\\ &H_{2}=(1+3)\%13=4,未发生冲突,插入位置 \text{\#}4\end{aligned} 初始散列地址H0=1%13=1,发生冲突(第1次)H1=(1+5)%13=6,发生冲突(第2次)H2=(1+3)%13=4,未发生冲突,插入位置#4
注:查找操作原理类似,根据探测序列依次对比各存储单元内的关键字。
若探测到目标关键字,则查找成功。
若探测到空单元,则查找失败。
七.删除元素
注:题目一定会说明具体是采用哪种探测序列(线性探测法、平方探测法、双散列法、伪随机序列法)
1.思路
- 先根据散列函数算出散列地址,并对比关键字是否匹配。若匹配,则"查找成功"
- 若关键字不匹配,则根据"探测序列"对比下一个地址的关键字,直到"查找成功"或"查找失败"
- 若"查找成功",则删除找到的元素
2.注意可能会踩的坑
1.注意
- 采用"开放定址法"时,删除元素不能简单地将被删元素的空间置为空,否则将截断在它之后的探测路径,可以做一个"已删除"标记,进行逻辑删除。
2.具体例子
- 例:长度为13的散列表状态如下图所示,散列函数 H(key)=key% 13,采用线性探测法解决冲突。

错误示范:删除元素15后查找元素1
- 计算元素15 的初始散列地址=15%13=2。对比位置#2,关键字不等于15;
- 根据线性探测法的探测序列,继续对比位置#3,关键字等于15;
- 删除元素15,清空位置#3
- 计算元素1的初始散列地址=1%13=1。对比位置#1,关键字不等于1;
- 根据线性探测法的探测序列,继续对比位置#2,关键字不等于1;
- 根据线性探测法的探测序列,继续对比位置#3,探测到空单元,查找失败。
- 分析:事实上1这个元素是在后一个位置,这就导致了错误
- 正确示范:

- 计算元素15 的初始散列地址=15%13=2。对比位置#2,关键字不等于15;
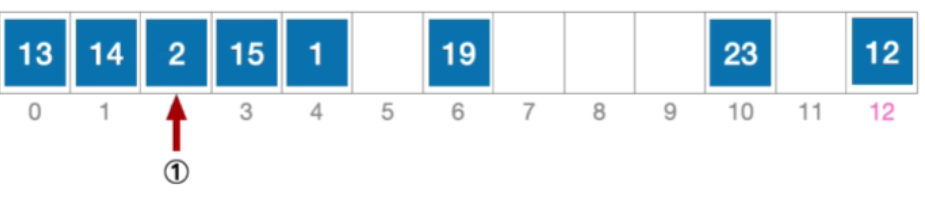
- 根据线性探测法的探测序列,继续对比位置#3,关键字等于15,逻辑删除元素15,将位置#3标记为"已删除"
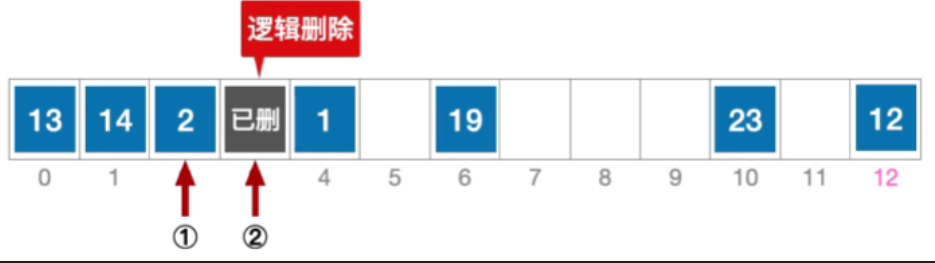
注:无论线性探测法、平方探测法、双散列法、伪随机序列法原理都一样。删除元素时,只能逻辑删除
注:新元素也可以插入到已被"逻辑删除"的地址
3.缺点
-
带来的问题:查找效率低下,散列表看起来很满,实则很空。

-
解决方法:可以不定期整理散列表内的数据。

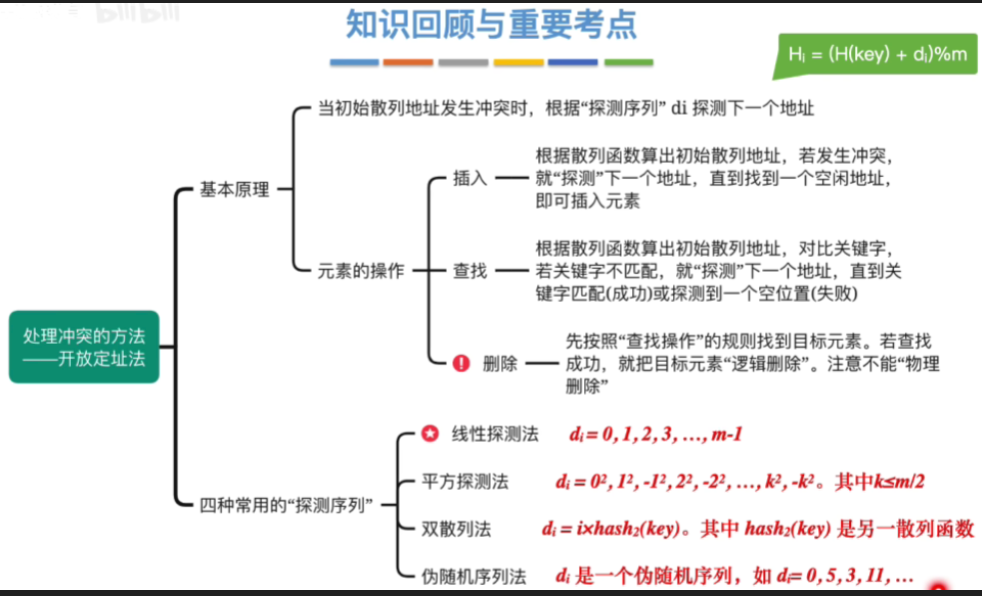
八.知识回顾与重要考点
九.拓展:"探测覆盖率"
1.概念
- 发生冲突的时候,我们介绍的这四种探测序列是否能够顺利地探测到散列表当中的每一个位置
2.线性探测法
1.结论
- 理想情况下,若散列表表长=m,则最多发生n-1次冲突即可"探测"完整个散列表。
- 采用线性探测法 ,一定可以探测到散列表的每个位置只要散列表中有空闲位置,就一定可以插入成功
2.具体例子
- 假设初始地址等于5,并且发生冲突

- 后一个位置会探测到6,这个位置还冲突
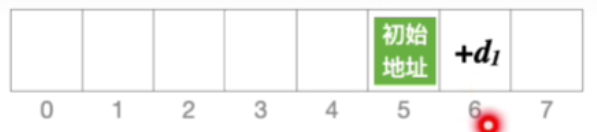
- 后一个位置就探测到7
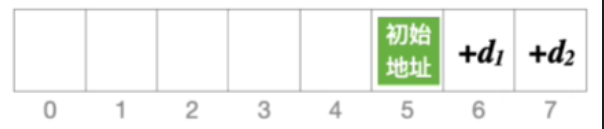
- 再往后是01234
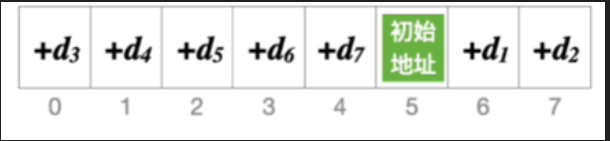
- 所有地址均被探测
3.平方探测法
1.结论
- 若散列表长度n是一个可以表示成4j+3的素数(如7、11、19),平方探测法就能探测到所有位置
- 采用平方探测法 ,至少可以探测到散列表中一半的位置,这意味着,即便散列表中有空闲位置,也未必能插入成功
2.具体例子
1.不能探测所有位置
- 假设初始地址为5且表长等于8且发生冲突
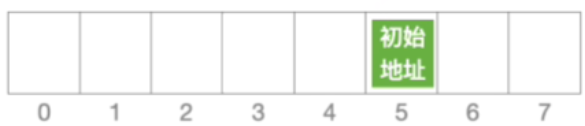
- 接下来应该是这样的

- 只探测了5641这几个地址,不能探测到所有位置
2.可以探测所有位置
- 假设初始地址为5且表长等于7且发生冲突
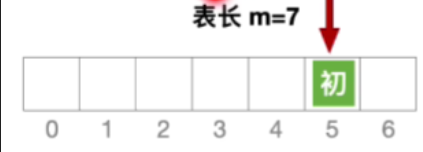
- 过程如下

- 可以找到所有的位置
4.双散列法
1.结论
- 双散列法未必能探测到散列表的所有位置。
- 双散列法的探测覆盖率取决于第二个散列函数hash(key)设计的是否合理。
- 若hash(key)计算得到的值与散列表表长m互质,就能保证双散列发可以探测所有单元
- 双散列法常用套路:令表长m本身就是质数,hash(key)=m-(key%m),此时无论key值是多少, h a s h 2 ( k e y ) hash_2(key) hash2(key)和m一定互质
2.具体例子
1.不能探测到所有地址
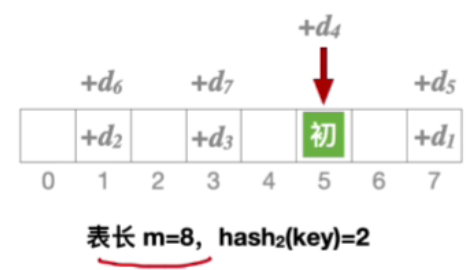
2.能探测到所有地址
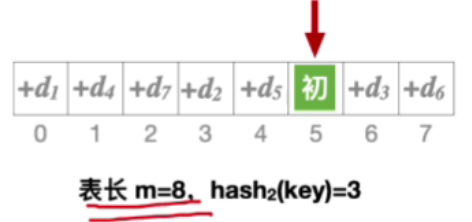
5.伪随机序列法
1.结论
- 采用伪随机序列法,是否能探测到散列表中全部位置,取决于伪随机序列的设计是否合理
2.具体例子
1.不能探测到所有地址
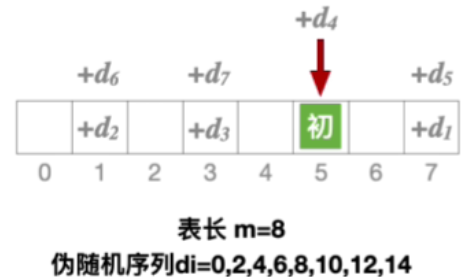
2.能探测到所有地址
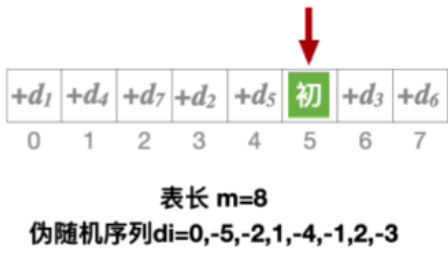
6.总结
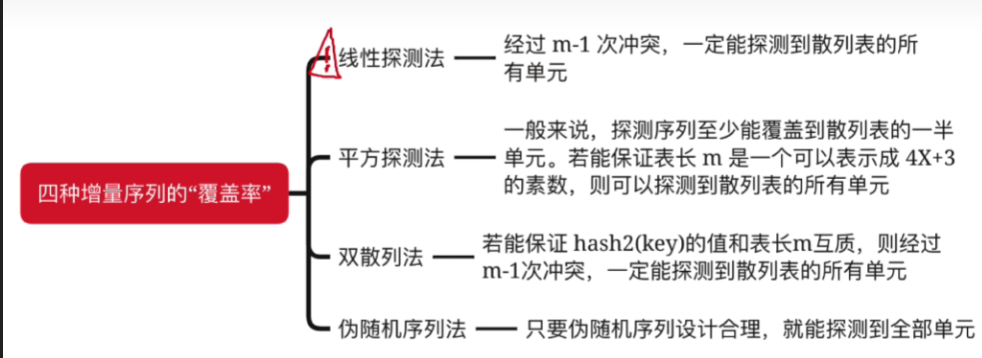
结论
二更😉,最近事情都忙完了,后面基本不会停更了
如果想查看更多章节,请点击:一、数据结构专栏导航页