红黑树底层原理拆解

文章目录

- 引言：红黑树的噩梦
- 核心心法：降维打击
- - [1. 颜色代表什么？](#1. 颜色代表什么？)
- 节点映射图解
- - [1. 2-节点 (存 1 个数) -> 黑色节点](#1. 2-节点 (存 1 个数) -> 黑色节点)
  - [2. 3-节点 (存 2 个数) -> 一黑一红](#2. 3-节点 (存 2 个数) -> 一黑一红)
  - [3. 4-节点 (存 3 个数) -> 黑父带俩红子](#3. 4-节点 (存 3 个数) -> 黑父带俩红子)
- 秒解红黑树的"魔法规则"
- - 规则一：不能有两个连续的红节点
  - 规则二：从根到叶子的黑色节点数必须相同
- 重新理解旋转与变色
- - [1. 变色 (Color Flip) = 节点分裂 (Split)](#1. 变色 (Color Flip) = 节点分裂 (Split))
  - [2. 旋转 (Rotation) = 内部归位](#2. 旋转 (Rotation) = 内部归位)
- 总结
- - References

引言：红黑树的噩梦

对于每一位 C++ 学习者来说，红黑树 (Red-Black Tree) 都是一道必须要跨过的坎。

打开《算法导论》或各种教材，你会被那一堆毫无感情的规则淹没：

节点是红色或黑色。
根是黑色。
所有叶子（NIL）是黑色。
每个红色节点必须有两个黑色的子节点（不能有两个连续红节点）。
从任一节点到其每个叶子的所有简单路径都包含相同数目的黑色节点（黑高平衡）。

最折磨人的还在后面：插入要看叔叔的脸色（红还是黑？），删除要看兄弟甚至兄弟的侄子。左旋、右旋、变色......当你费尽心力死记硬背下来，过两个月去面试，发现脑子里只剩下一团浆糊。

为什么这些规则这么奇怪？为什么要规定"不能双红"？为什么只算"黑高"？

其实，红黑树的规则并非凭空捏造。如果你觉得它晦涩难懂，是因为你只看到了它的**"二叉树形态"**。今天，我们换一个"上帝视角"，通过 2-3-4 树 来彻底解构红黑树。

核心心法：降维打击

一句话道破天机：

红黑树本质上是 2-3-4 树（一种 B 树）的二叉树实现。

2-3-4 树是一种绝对平衡的树，它的所有叶子节点永远在同一层。但为了在计算机中更方便地实现（利用现有的二叉搜索树逻辑），我们将 2-3-4 树的节点"拆解"成了二叉树的样子。

1. 颜色代表什么？

在红黑树中，颜色不仅仅是涂装，它代表了物理连接方式：

黑色节点：代表 2-3-4 树中的**"硬连接"**（垂直生长），表示树的高度真的增加了一层。
红色节点：代表 2-3-4 树中的**"胶水"**（水平连接）。红色节点并不独立，它和它的黑色父节点在逻辑上属于同一个 2-3-4 大节点。

如上图所示，一个简单的 2-3-4 树节点直接对应一个红黑树的黑色节点。

节点映射图解

让我们看看 2-3-4 树的三种节点是如何映射成红黑树结构的。一旦理解了这个，后续规则不攻自破。

1. 2-节点 (存 1 个数) -> 黑色节点

这是最基础的情况。2-3-4 树里的一个独立节点，直接对应红黑树里的一个黑色节点。

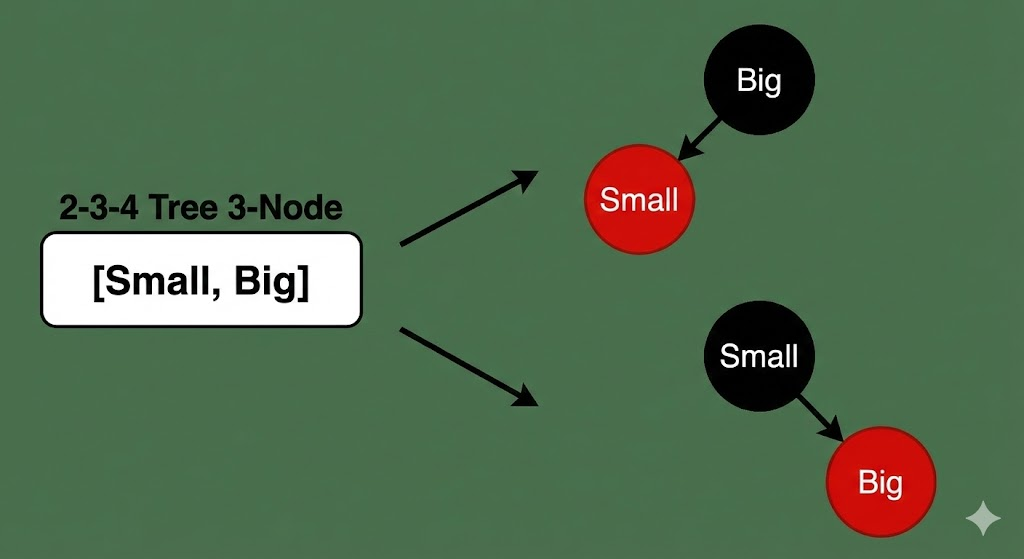
2. 3-节点 (存 2 个数) -> 一黑一红

在 2-3-4 树中，我们允许两个数 [Small, Big] 挤在一个节点里。

但在二叉树中，一个位置只能坐一个人。怎么办？上下坐！

我们可以把 Big 染黑放在上面，把 Small 染红挂在左边。
也可以把 Small 染黑放在上面，把 Big 染红挂在右边。

这就是为什么红黑树里会有"左倾"或"右倾"的概念。虽然它们在二叉树里是父子关系，但在 2-3-4 树眼里，它们是平起平坐的"室友"。

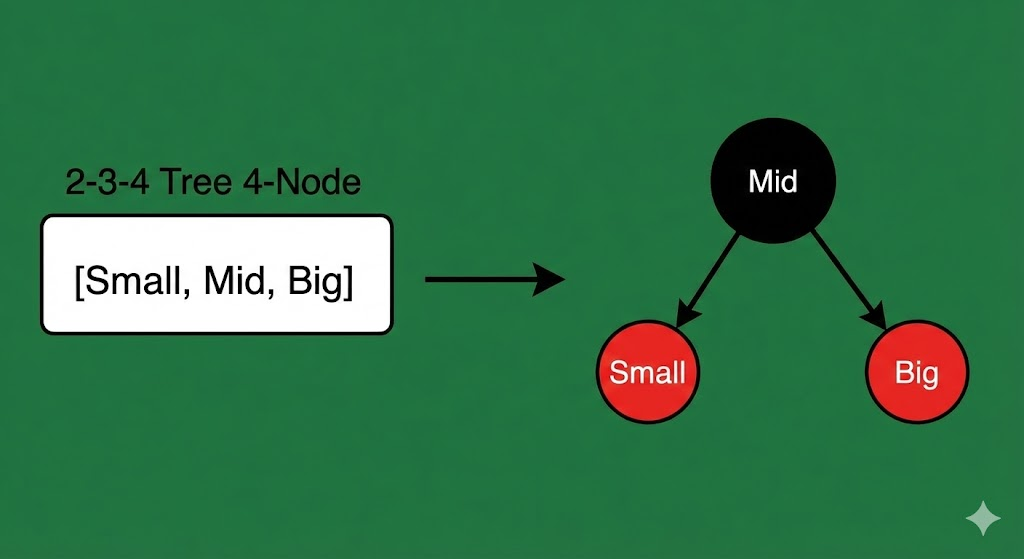
3. 4-节点 (存 3 个数) -> 黑父带俩红子

这是 2-3-4 树中容量最大的节点 [Small, Mid, Big]。

映射到红黑树，就是把中间的 Mid 顶上去做黑色父节点，两边的 Small 和 Big 做红色子节点。

秒解红黑树的"魔法规则"

建立了映射关系后，我们再回头看那些死记硬背的规则，你会发现它们全是废话。

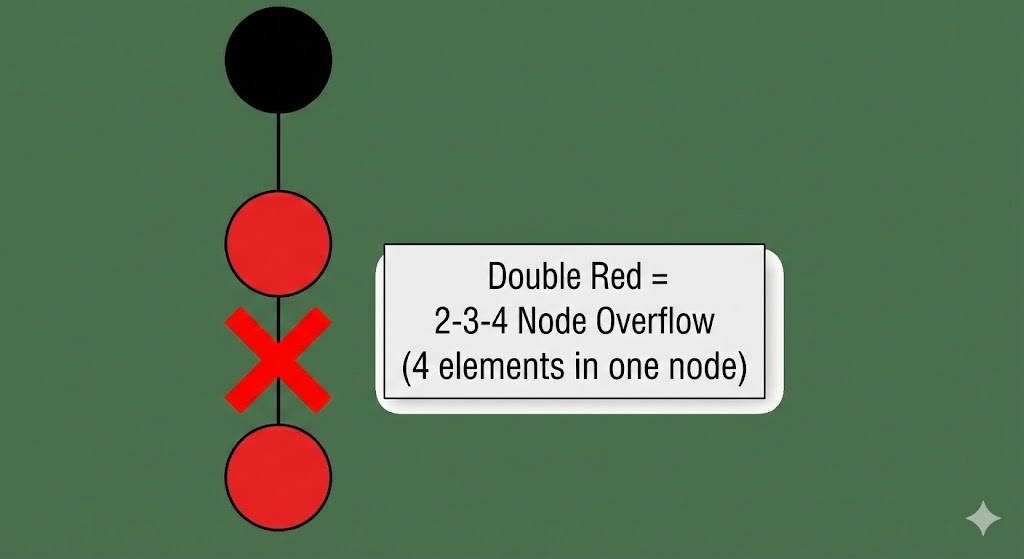
规则一：不能有两个连续的红节点

疑问：为什么？
上帝视角 ：红色代表"水平融合"。如果你有 黑 -> 红 -> 红，这意味着你想把 3 个元素融合在那个黑色节点里（算上黑色节点自己，一共 4 个元素）。

然而，2-3-4 树规定一个节点最多只能存 3 个数（即 4-节点）。

结论：双红 = 2-3-4 节点溢出（Overflow）。 必须进行分裂操作。

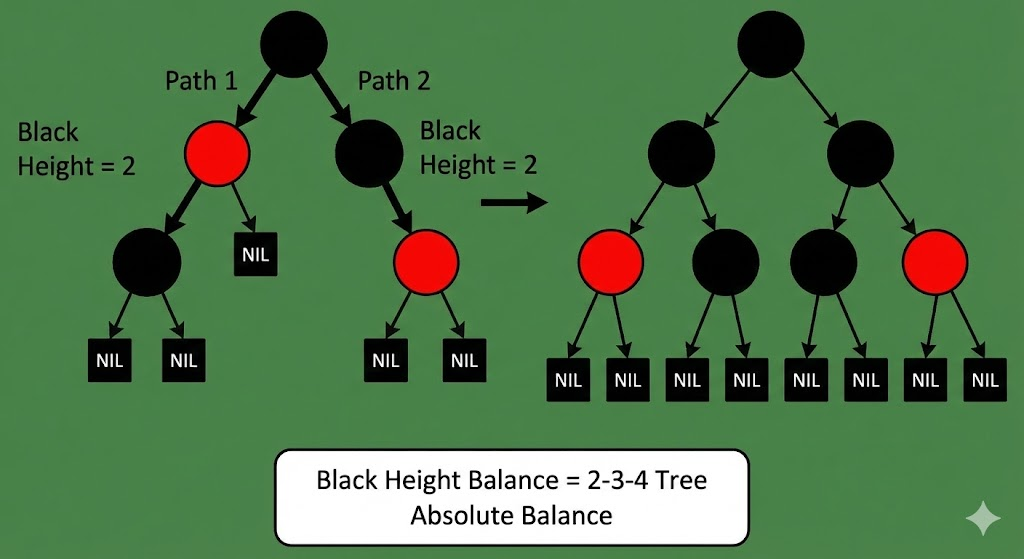
规则二：从根到叶子的黑色节点数必须相同

疑问：为什么不算红色？
上帝视角 ：2-3-4 树作为 B 树的一种，它是绝对平衡的，所有叶子都在同一层。

在映射过程中，只有黑色边代表向下一层，红色边只是在节点内部横向折叠。如果我们忽略红色节点（把它们压扁回父节点里），剩下的黑色骨架就是那棵绝对平衡的 2-3-4 树。

结论：黑高平衡 = 2-3-4 树的绝对平衡性。

重新理解旋转与变色

当你写代码遇到需要调整树结构时，不要去背代码，想一想你在操作 2-3-4 树。

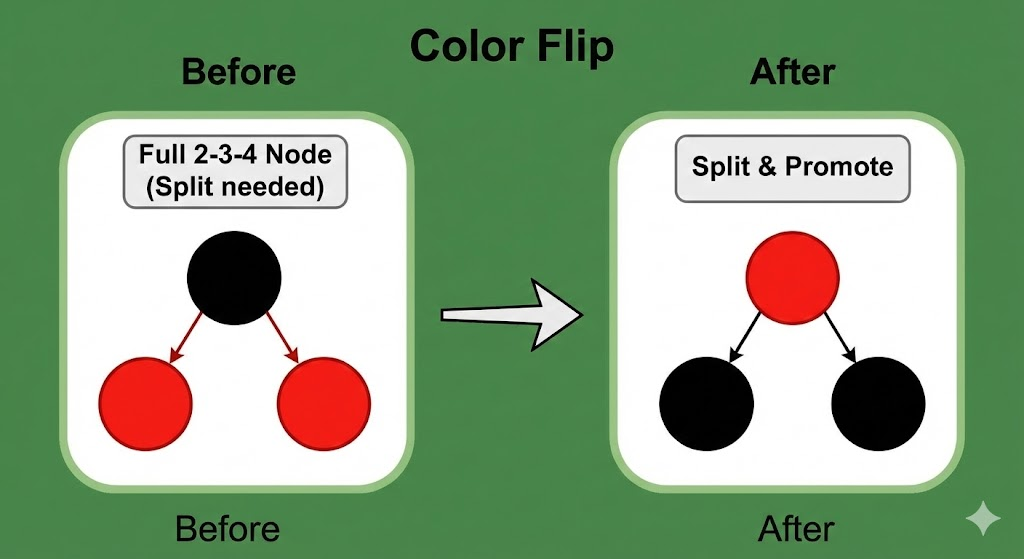
1. 变色 (Color Flip) = 节点分裂 (Split)

当你插入一个新节点，发现父节点是红，叔叔也是红。

这对应什么场景？
父亲红 + 叔叔红 = 爷爷节点（黑）已经挂了两个红色儿子。

这意味着爷爷对应的 2-3-4 节点里已经有 [左红, 爷黑, 右红] 三个元素了，这是一个满载的 4-节点。

现在你还要往里插？爆了！

2-3-4 树操作逻辑：遇到节点满载，会把中间元素（爷爷）向上进位，两边元素分裂。
红黑树操作：爷爷变红（向上进位，去粘它的父节点），父亲和叔叔变黑（独立门户）。

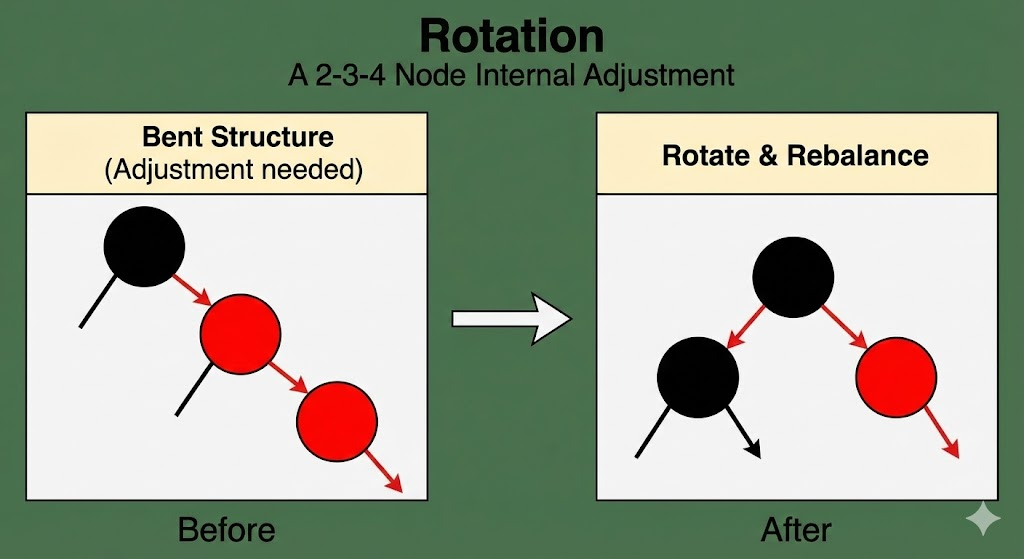
2. 旋转 (Rotation) = 内部归位

当你插入一个新节点，父节点红，叔叔是黑（或不存在）。

这对应什么场景？

这意味着当前的 2-3-4 节点还没满（还能塞），但是你的插入位置让这个节点在二叉树下的形态歪了。比如出现了"直线型"双红，或者"折线型"双红。

操作逻辑 ：旋转就是把这个歪掉的形状"掰正"，让它重新变成一个标准的 黑父 + 红子 的形态（即合法的 3-节点）。

总结

学习数据结构，最忌讳陷入代码细节的泥潭。

对于红黑树：

新手看到的是 LeftRotate(node) 和 node->color = RED。
高手看到的是 2-3-4 树的分裂（Split）与合并（Merge）。

下次面试被问到红黑树时，试着在脑海里画一棵 2-3-4 树。你不仅能轻松推导出所有规则，还能给面试官讲讲这背后的数学同构之美------这才是真正的"内功"。

References

Algorithms, 4th Edition by Robert Sedgewick and Kevin Wayne (关于红黑树与 2-3 树同构的经典论述)
Introduction to Algorithms (CLRS) (关于 B 树性质的论述)