克莱姆法则（Cramer's Rule）
克莱姆法则是求解 n 阶线性方程组 的重要方法，核心是通过行列式判断方程组解的存在性、唯一性，并直接用行列式表示解。以下是完整且步骤清晰的证明过程：
一、前置定义与前提条件
1. 4 阶线性方程组的标准形式
设 4 阶线性方程组为：
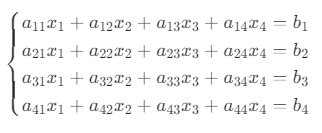
其中：
是未知数；
2. 关键行列式定义
- 系数行列式：由方程组系数构成的 4 阶行列式，记为 D：
- 替换行列式 ：将 D 的第 j 列（系数
3. 前提假设
克莱姆法则的适用条件：系数行列式 。
二、克莱姆法则的结论
若 n 阶线性方程组的系数行列式 ，则方程组有且仅有唯一解：
三、证明过程（分 3 步：存在性→唯一性→解的形式）
步骤 1：证明 "解的存在性"------ 验证 满足方程组
我们需要验证：满足原方程组的每一个方程。
需验证：对任意 i=1,2,3,4（对应 4 个方程），均有
两边同乘 D，等价于证明：
第一步：展开替换行列式
将 按第 j 列展开（第 j 列是
），根据 4 阶行列式按列展开法则：
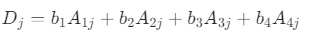
其中 是 D 中
的代数余子式（注：
的第 j 列代数余子式与 D 的第 j 列代数余子式完全相同，因为划去第 k 行第 j 列后，剩余元素与 D 一致）
代入等式 (1) 左边
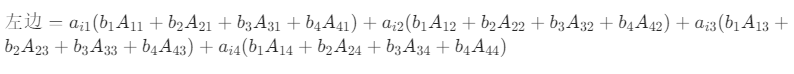
交换求和顺序（先对 j 求和，再对 k 求和）：
左边=
第三步：利用行列式展开性质化简
根据 4 阶行列式的核心性质：
- 当 k=i 时，
- 当
因此，等式 (2) 中仅 k=i 的项非零，其余项为 0：
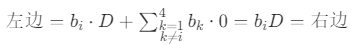
故 满足第 i 个方程，由 i 的任意性，该解满足所有 4 个方程，"存在性" 得证。
四、特殊情况：齐次线性方程组
若原方程组的常数项全为 0（即 b1=b2=⋯=bn=0），则：
- 替换行列式
- 若
推论：齐次线性方程组有非零解的充要条件是其系数行列式 D=0。
五、证明总结
克莱姆法则的证明核心依赖 行列式的按行 / 列展开性质（代数余子式的正交性）：
- 构造候选解
- 利用齐次方程组的性质证明解唯一（唯一性）；
- 结合前两步，确定唯一解的形式。
该法则的意义在于：当 时，直接通过行列式给出解的表达式，无需高斯消元，且明确了 "行列式非零" 与 "解唯一" 的等价关系。