第k个最小元素
问题描述：
给定一个数组（无序），输出该数组中第k个最小元素，即按从小到大排序的第k个元素。
很简单的可以想到，先排序后输出，这样最小时间复杂度为，能不能用分治解决呢？
我们可以任选数组中的一个元素，将比这个元素小的元素放进一个数组，比这个元素大的元素放进另一个数组
以4、7、8、2、1、9数组为例，我们想求其中第3小的元素：假设选中7，那么从头开始比较：
4比7小，8比7大，2、1比7小，9比7大
得到数组L：【4、2、1】；数组R：【8、9】通过这种方法，我们将大问题分解成了两个小问题，L.length=3，R.length=2
由于想求其中第3小的元素，由于3<=L.length，所以第3小的元素一定在L中，再使用相同的方法：任选L中的任意一个元素，分为两个数组，如此递归下去。
如果想求其中第5小的元素，由于5>L.length，所以第5小的元素一定在R中，再使用相同的方法：任选R中的任意一个元素，分为两个数组，如此递归下去。
如果想求其中第4小的元素，由于4恰好等于L.length+1，所以第4小的元素恰好就是选择的这个元素，递归结束。这种情况，就可以作为递归出口。
简单总结一下算法
- 选枢轴：从数组 A 中选一个元素 A_i作为 "枢轴（pivot）"；
- 初始化集合：创建两个集合 S_+（存比 A_i大的元素）、S_-（存比 A_i小的元素）；
- 遍历划分 ：遍历数组中每个元素 A_j：
- 若 A_j > A_i，将 A_j 加入 S_+；
- 否则 A_j <= A_i，将 A_j 加入 S_-；
- 判断递归方向 ：
- 若 |S_-| = k-1：说明 A_i 正好是第 k 小元素（因为 S_- 就有k-1个比它小的元素），直接返回 A_i；
- 若 |S_-| > k-1：第 k 小元素在 S_- 中，递归调用 {SELECT}(S_-, k)；
- 若 |S_-| < k-1：第 k 小元素在 S_+ 中，调整 k 为 k - |S_-| - 1（因为 S_- 有 |S_-| 个元素，A_i是第 |S_-|+1小，所以要在 S_+ 中找 "第 k - (|S_-|+1) 小" 的元素），递归调用 {SELECT}(S_+, k - |S_-| - 1)。
现在只有一个问题：
如何选择枢轴
我们先来看两个极端情况：
- 每次都选最大（小）的元素 ：这样其实和分治（一）中提到的不均匀分解的归并排序一样，子问题的规模每次只会下降1；
- 每次都选最中间的元素：这样每次都是均分，问题的规模指数级下降；
回忆一下之前的主定理：
上一篇文章中提到，a和b似乎指的都是把原问题分为几部分，难道a和b不应该相等吗？这里就会解释这个问题。
每次都选最大（小）元素 ：递归式：，时间复杂度为
（这里由于a=b=1，log以1为底，1的对数是没有意义的，直接套用递归式就可以得到n个
相加，所以时间复杂度是
）
每次都选最中间元素 ：递归式：，时间复杂度为
（这里a=1，b=2，d=1，即第三种情况，这里就出现了我们所说的，a和b不相等的情况，原因在于我们虽然把子问题分解成了两个，但并不对两个子问题都进行继续分解，而是只选其一）
从这两种极端情况可以看出，枢轴的选择对算法影响非常大，最坏的情况甚至会退化到不如先排序后选择，而最好的情况是线性的。
下面我们证明，即使不选择最好的枢轴（红色），只需选择次好（即中间的一个范围内的所有元素，绿色），该算法的时间复杂度仍然是线性的。
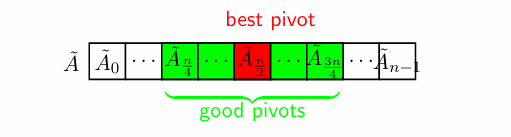
每次选近中心元素 （存在固定比例，使得比枢轴大 / 小的元素数≥
，如
- 子问题规模同样指数级减小
- 递归式：
，展开后时间复杂度仍为
由主定理，是可求出范围的，事实上，
只要不大于1，该算法的时间复杂度都是线性的，即只要不是每次都选到最小或最大，该算法的时间复杂度都是线性的。证明如下：
三种枢轴的选择方法
1、中位数的中位数
这种方法是好理解的，它通过 "分组求中位数→递归求中位数的中位数" 选择枢轴，确保枢轴是 "近中心元素"（至少 30% 的元素大于 / 小于枢轴），是确定性线性时间的枢轴选择方法。
步骤如下：
- 分组：将数组按 5 个元素一组划分（分组大小为 5 是算法稳定性的关键，7 个及以上也有效，3 个则退化为 O (n log n)）；
- 求组中位数：对每组排序，取中位数（共得到⌈n/5⌉个组中位数）；
- 递归求中位数的中位数：对组中位数构成的新数组，递归调用 SELECT 算法求其中位数，该中位数即为最终枢轴 M；
- 划分数组：以 M 为枢轴，将原数组划分为 S⁻（小于 M）和 S⁺（大于 M），进入对应子问题递归。
来看一个例子：
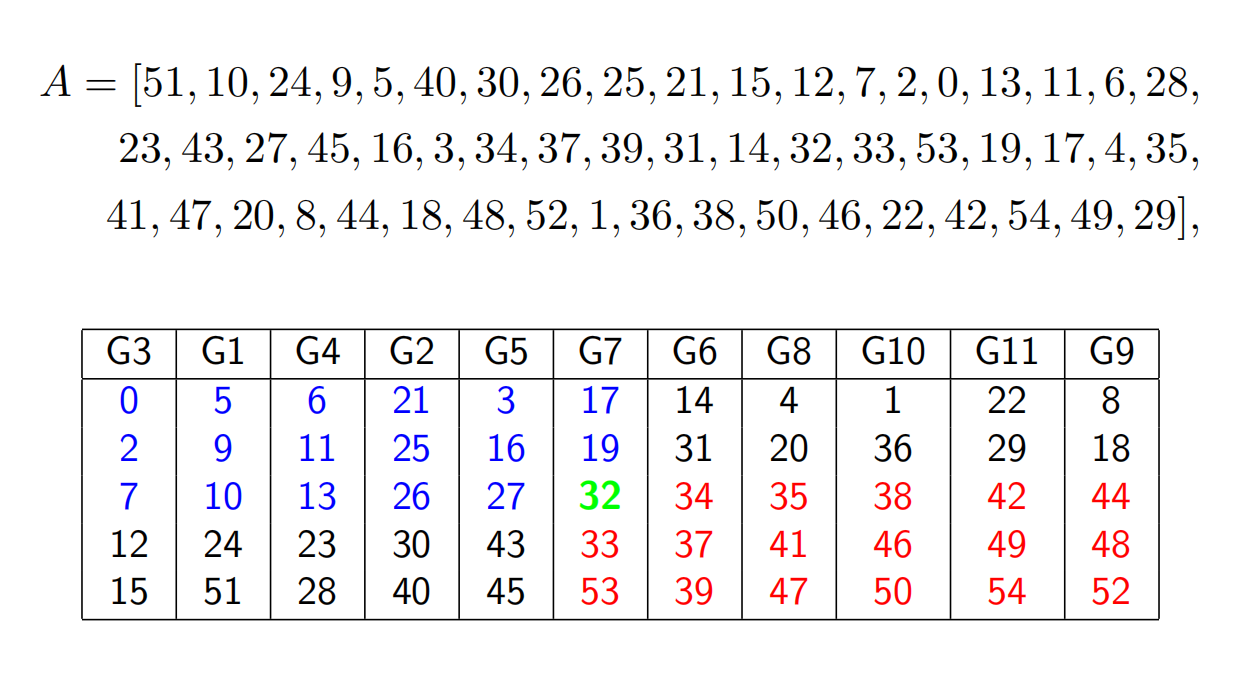
这种策略，枢轴 M 能保证至少个元素大于 M、
元素小于 M，子问题规模最大为
，确保指数级减小。我们刚刚提到，7个及以上为一组也可以有这样的效果，但3个一组不行，这同样也可以用主定理证明，不再赘述。
2、随机选择------QUICKSELECT
从数组中均匀随机选择一个元素作为枢轴，无需预处理，是实践中最常用的次好枢轴选择方法。这和快排非常类似。（实际上，第k个最小元素这个问题和快排是高度相似的)
步骤如下：
- 随机选枢轴：无预处理，直接从数组中随机抽取一个元素 Ai 作为枢轴；
- 划分数组：将元素分为 S⁻（小于 Ai）和 S⁺（大于 Ai）；
- 递归子问题：根据 k 与 | S⁻| 的关系，递归处理 S⁻或 S⁺（仅需处理一个子问题）。
我们之前证明次好枢轴也能让该算法的时间复杂度是线性的 时提到，只要＜1即可，也就是随机选择可以实现线性时间复杂度的原因。当然，严谨的证明比较复杂，涉及概率论的知识，不再赘述。
3、Floyd-Rivest 算法
该算法实际上是对SELECT的改进，并不单纯的选择枢轴
通过随机抽样 + 区间估计 选择两个枢轴 u 和 v，将数组划分为 "小于 u""介于 u-v 之间""大于 v" 三部分，仅对中间子集递归，是兼顾效率与稳定性的优化方法。核心在于：若随机样本的规模足够大，样本会是整体集合的良好代表，样本的中位数是 "整体集合中位数" 的无偏估计，因此可以通过样本确定一个小区间，该区间以极高概率包含整体集合的中位数。
步骤如下：
- 抽取随机样本：从原数组A中抽取一个小的随机样本S（允许重复抽样）；
- 选双枢轴u,v：递归调用 Floyd-Rivest 算法，从样本S中选出两个枢轴u和v，使得区间[u,v]以高概率包含A的第k小元素；
- 划分数组为三部分 ：将A 分为三个不相交的子集：
- L：所有小于u的元素；
- M：所有介于u和v之间的元素；
- H：所有大于v的元素；
- 优化划分的比较顺序 ：根据k与
- 递归求解：在L/M/H中选择对应的子集，递归执行算法，最终找到第k小元素。
这个算法其实和随机枢轴的SELECT差不多，只不过它把子问题划分了三类，而且应用了一些概率的知识。介绍这种算法，主要是为了引出一种快速寻找中位数的算法------LAZYSELECTMEDIAN。
LAZYSELECTMEDIAN 算法
这是专门用于找中位数的简化变体，步骤如下：
- 抽取随机样本：从A中随机抽取r个元素，得到样本S；
- 从样本选双枢轴u,v ：
- 排序样本S；
- 选u为S的
- 划分数组为三部分：与 Floyd-Rivest 一致，分为L（<u）、M（u、v之间）、H（>v）；
- 检查M的约束（核心步骤） ：确保M同时满足两个条件：
- 包含中位数 ：
- 规模适中 ：
- 包含中位数 ：
- 输出中位数 ：排序M，返回M中第
看一个例子理解一下
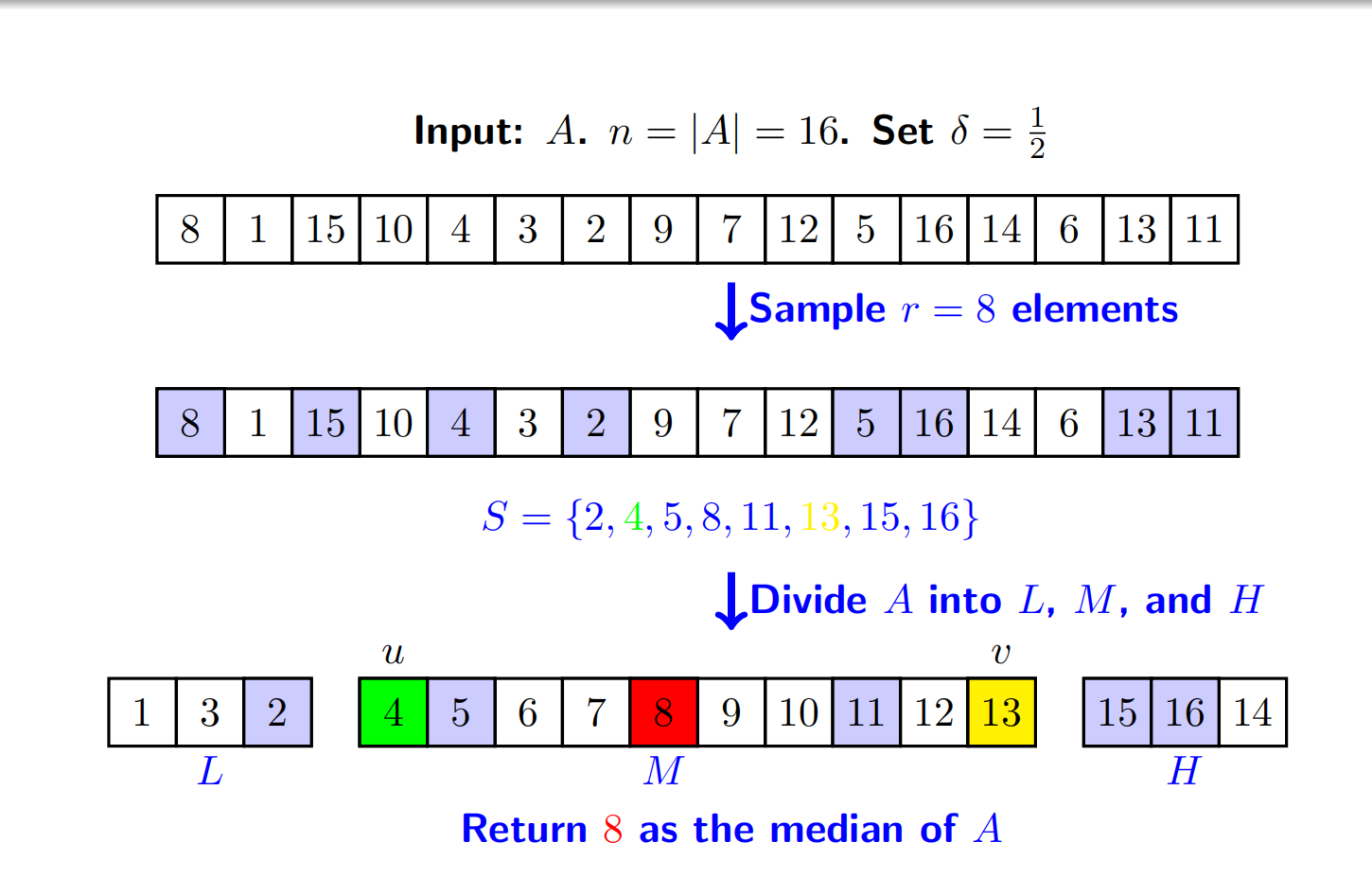
- 输入数组：A = [8,1,15,10,4,3,2,9,7,12,5,16,14,6,13,11]；
- 抽取随机样本：从A中抽样r=8个元素，得到样本S = {2,4,5,8,11,13,15,16\}；
- 选双枢轴u,v ：根据
- 划分数组为L/M/H ：
- L：小于u=4的元素[1,3,2]；
- M：介于4和13之间的元素[4,5,6,7,8,9,10,11,12,13]；
- H：大于v=13的元素[15,16,14]；
- 输出中位数 ：排序M后，取M中第
要注意，选择双枢轴之后是对原样本A进行划分，不是S。
这个过程是很明确的，可能有些疑问：
1、M中包含中位数的概率有多高
2、有没有一种可能，**M的约束（即包含中位数和规模适中）**一直无法满足，导致算法死循环？
只有理论上有这种可能，毕竟概率为0的事件也可能发生。事实上可以通过计算证明，这种算法**单次通过（不重新抽样）的概率极高，而且M包含中位数的概率也非常高。**不过证明过程仍然需要用到概率论的知识，课件上有，再此不再赘述。
相较于之前的两种方式，由于对样本进行的抽样，且下降速度更快，Floyd-Rivest 算法更加适用于大量数据。
分治的后面还有大数乘法、矩阵乘法、最近点对问题（CLOSESTPAIR problem）三个问题。我印象中老师上课讲了矩阵乘法，其余两个应该是没讲吧（？），后续有时间会继续研究。下面可能先补DP的内容