线代第二章矩阵第一课：矩阵的概念

矩阵的概念

矩阵是线性代数的核心工具之一，是由数（或其他代数对象）按矩形排列形成的数表，广泛应用于线性方程组求解、线性变换表示、数据分析等领域。

一、矩阵的定义

由 个数 排成的 m 行 n 列 的矩形数表，称为 m×n 矩阵，记作：

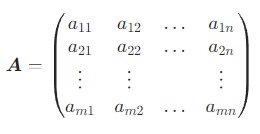
​​​也可简记为 或

核心术语说明

1. 元素 ：数表中的每个数 称为矩阵的元素，下标 i 表示行标 （第 i 行），下标 j 表示列标（第 j 列）。
2. 行与列 ：横向的数为行 ，共 m 行；纵向的数为列，共 n 列。

二、矩阵的常见分类

1. 按行数和列数分类

• 方阵 ：若 m=n，则称 A 为 n 阶方阵（行数 = 列数）。
• 例如 2 阶方阵： ； 3 阶方阵：。
• 行矩阵 ：若 m=1，则称 A 为 行矩阵 （只有 1 行），也叫行向量，例如。
• 列矩阵 ：若 n=1，则称 A 为 列矩阵 （只有 1 列），也叫列向量，例如 。

2. 按元素性质分类

• 零矩阵 ：所有元素都为 0 的矩阵，记作 ，例如 。
• 对角矩阵 ：n 阶方阵中，除主对角线 （从左上到右下的元素 ）外，其余元素都为 0，记作 A=diag()，例如：
• 单位矩阵 ：主对角线元素全为 1 的对角矩阵，记作 ，例如 3 阶单位矩阵：

单位矩阵的核心性质：对任意 m×n 矩阵 A，有 。

• 三角矩阵
• 下三角矩阵：主对角线上方元素全为 0 的 n 阶方阵，例如：

​​​

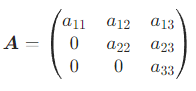
• 上三角矩阵：主对角线下方元素全为 0 的 n 阶方阵，例如：

​​​

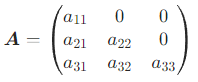
3. 按特殊性质分类

• 对称矩阵 ：n 阶方阵满足（即 ， 为 A 的转置矩阵），例如：
• 反对称矩阵 ：n 阶方阵满足 （即 ），其主对角线元素全为 0，例如：

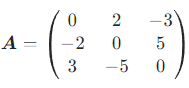
三、矩阵与行列式的区别

矩阵和行列式是线性代数中两个易混淆的概念，核心区别如下：

特征	矩阵	行列式
本质	矩形数表（无值）	数表对应的一个数值
形状	m×n 任意矩形	必须是 n×n 方阵
符号	用圆括号 () 或方括号 \[\]	用竖线 ∣∣
运算规则	有加法、数乘、乘法等运算	是一个数，遵循数的运算规则

内容来源-B站宋浩老师