【算法基础篇】（二十九）路径类线性 DP 保姆级教程：从矩阵到迷宫，覆盖 4 道经典题 + 优化神技

---

目录

前言

[一、路径类 DP 核心逻辑：用 "位置" 定义状态，用 "方向" 推导转移](#一、路径类 DP 核心逻辑：用 “位置” 定义状态，用 “方向” 推导转移)

[1.1 路径类 DP 的本质：位置即状态，移动即转移](#1.1 路径类 DP 的本质：位置即状态，移动即转移)

[1.2 路径类 DP 解题四步曲（通用模板）](#1.2 路径类 DP 解题四步曲（通用模板）)

第一步：明确定义状态（最关键）

第二步：推导状态转移方程（核心逻辑）

第三步：初始化（避免逻辑漏洞）

第四步：确定填表顺序（保证正确性）

[1.3 路径类 DP 的两大优化方向](#1.3 路径类 DP 的两大优化方向)

[二、经典例题实战：从基础到进阶，吃透路径类 DP](#二、经典例题实战：从基础到进阶，吃透路径类 DP)

[例题 1：数字三角形（洛谷 P1216）------ 路径类 DP 入门题](#例题 1：数字三角形（洛谷 P1216）—— 路径类 DP 入门题)

题目描述：从金字塔顶端到低端的最大路径和

思路拆解（四步曲套用）

第一步：定义状态

第二步：推导状态转移方程

第三步：初始化

第四步：填表顺序

代码实现（基础版：二维数组）

[优化：滚动数组（空间从 O (r²)→O (r)）](#优化：滚动数组（空间从 O (r²)→O (r)）)

优化解析

[例题 2：矩阵的最小路径和（牛客 DP11）------ 路径类 DP 的 "导航基础题"](#例题 2：矩阵的最小路径和（牛客 DP11）—— 路径类 DP 的 “导航基础题”)

题目描述：从左上角到右下角的最小代价

思路拆解（四步曲套用）

第一步：定义状态

第二步：推导状态转移方程

第三步：初始化

第四步：填表顺序

[代码实现（基础版：二维数组 + 边界优化）](#代码实现（基础版：二维数组 + 边界优化）)

[代码解析：为什么用 "无穷大" 初始化？](#代码解析：为什么用 “无穷大” 初始化？)

[优化：滚动数组（空间 O (nm)→O (m)）](#优化：滚动数组（空间 O (nm)→O (m)）)

优化解析

[例题 3："木" 迷雾森林（牛客网）------ 路径类 DP 的 "障碍迷宫题"](#例题 3：“木” 迷雾森林（牛客网）—— 路径类 DP 的 “障碍迷宫题”)

题目描述：从左下角到右上角的路径计数

思路拆解（四步曲套用）

第一步：定义状态

第二步：推导状态转移方程

第三步：初始化

第四步：填表顺序

代码实现（基础版：二维数组）

代码解析：为什么用scanf而不是cin？

[优化：滚动数组（空间 O (mn)→O (n)）](#优化：滚动数组（空间 O (mn)→O (n)）)

优化解析

[例题 4：过河卒（洛谷 P1002）------ 路径类 DP 的 "障碍 + 特殊约束题"](#例题 4：过河卒（洛谷 P1002）—— 路径类 DP 的 “障碍 + 特殊约束题”)

题目描述：卒避马的路径计数

思路拆解（四步曲套用）

第一步：定义状态

第二步：推导状态转移方程

第三步：初始化

第四步：填表顺序

[代码实现（基础版：二维数组 + 控制点标记）](#代码实现（基础版：二维数组 + 控制点标记）)

[代码解析：为什么用long long？](#代码解析：为什么用long long？)

[优化：边界统一处理（避免单独初始化第一行 / 列）](#优化：边界统一处理（避免单独初始化第一行 / 列）)

优化解析

[三、路径类 DP 通用解题模板总结](#三、路径类 DP 通用解题模板总结)

[1. 问题分析](#1. 问题分析)

[2. 状态定义](#2. 状态定义)

[3. 转移方程推导](#3. 转移方程推导)

[4. 初始化](#4. 初始化)

[5. 填表顺序](#5. 填表顺序)

[6. 优化技巧](#6. 优化技巧)

总结

---

前言

如果你玩过《推箱子》这类游戏，一定对 "规划路径" 不陌生 ------ 从起点到终点，每一步都要考虑方向、障碍、收益，最终找到最优路线。而算法世界里的 "路径类线性 DP"，本质就是解决这类 "地图导航" 问题的利器。

作为线性 DP 的重要分支，路径类 DP 的核心特点是状态与 "位置" 强绑定 ------ 无论是二维矩阵的(i,j)坐标，还是环形地图的特殊点位，状态定义都离不开 "当前走到哪了"，状态转移则围绕 "下一步能往哪走" 展开。

相比于基础线性 DP（如最大子段和），路径类 DP 更贴近 "场景化问题"，比如求最小路径和、统计可行路径数、避开障碍找最优解等。但只要掌握 "位置定义状态，方向推导转移" 的核心逻辑，就能轻松拿下这类题。

今天这篇文章，就带大家从 "入门到精通" 吃透路径类线性 DP：从最经典的 "数字三角形" 入手，到矩阵最小路径和、迷雾森林迷宫、过河卒避马难题，每道题都拆解清楚 "状态设计→转移推导→代码实现→优化技巧"，最后再总结通用解题模板。哪怕你是刚接触 DP 的新手，跟着步骤走也能完全掌握！下面就让我们正式开始吧！

---

一、路径类 DP 核心逻辑：用 "位置" 定义状态，用 "方向" 推导转移

在正式讲例题前，我们先搞懂路径类 DP 的 "底层逻辑"------ 为什么它能解决地图路径问题？核心思路是什么？

1.1 路径类 DP 的本质：位置即状态，移动即转移

路径类 DP 的核心是把 "当前所在位置" 作为状态的核心要素 ，比如在二维矩阵中，用**dp[i][j]**表示 "走到第 i 行第 j 列时的某种目标值（如路径和、方案数）"。而状态转移的本质，就是 "从当前位置能到达的下一个位置，如何继承当前状态的信息"。

举个简单例子：如果只能向右或向下走，那么走到(i,j)的前一步，只能是(i-1,j)（从上方下来）或(i,j-1)（从左方过来）。这种 "移动方向限制"，直接决定了状态转移方程的推导逻辑。

1.2 路径类 DP 解题四步曲（通用模板）

和所有线性 DP 一样，路径类 DP 也有固定的解题流程，记住这四步，90% 的题都能套用：

第一步：明确定义状态（最关键）

用dp[i][j]表示"走到位置(i,j)时的目标值"，目标值根据题目需求确定：

• 求最小 / 最大路径和 ：dp[i][j] = 走到(i,j)的最小 / 最大路径和；
• 求可行路径数 ：dp[i][j] = 走到(i,j)的不同路径总数；
• 求特殊约束路径 ：dp[i][j] = 走到(i,j)且满足某条件（如不经过障碍）的目标值。

第二步：推导状态转移方程（核心逻辑）

根据 "允许的移动方向" 和 "题目目标" 推导：

• 方向限制：比如只能向右 / 向下 / 向上 / 向左，或多方向结合；
• 目标限制：比如求最小和就取前序状态的最小值，求方案数就累加前序状态的方案数；
• 特殊约束 ：比如遇到障碍时dp[i][j] = 0（不可达），遇到特殊点时跳过。

第三步：初始化（避免逻辑漏洞）

路径类 DP 的初始化通常围绕 "起点" 和 "边界"：

• 起点初始化 ：比如起点(1,1)的**dp[1][1] = 起点本身的值（路径和）或 1（方案数）**；
• 边界初始化 ：比如第一行只能从左向右走，所以dp[1][j] = dp[1][j-1] + a[1][j]（路径和）；第一列只能从上向下走，同理。

第四步：确定填表顺序（保证正确性）

填表顺序必须满足 "计算当前状态时，依赖的前序状态已计算完成"：

• 若只能向右 / 向下：从左到右、从上到下填表；
• 若只能向上 / 向右：从下到上、从左到右填表；
• 若有环形或多方向：需特殊处理（如倍增数组），但基础路径类 DP 很少涉及。

1.3 路径类 DP 的两大优化方向

路径类 DP 的优化主要集中在 "空间" 上，因为二维dp数组在矩阵规模较大时（如1e3×1e3）会占用较多内存，常见优化技巧有：

1. 滚动数组优化 ：若**dp[i][j]**只依赖上一行（i-1）或同一行的前半部分（j-1），可用一维数组替代二维数组，空间复杂度从O(nm)降至O(m)；
2. 边界压缩：将矩阵的无效区域（如障碍、越界位置）提前处理，减少不必要的计算。

二、经典例题实战：从基础到进阶，吃透路径类 DP

接下来我们通过 4 道经典例题，一步步套用 "解题四步曲"，从简单到复杂，彻底掌握路径类 DP 的逻辑。每道题都会详细拆解思路，附上完整代码和优化版本，确保你能看懂、会用、能举一反三。

例题 1：数字三角形（洛谷 P1216）------ 路径类 DP 入门题

题目描述：从金字塔顶端到低端的最大路径和

给定一个r行的数字三角形（金字塔形状），每次只能走到左下方或右下方的点，求从顶端走到低端任意位置的路径上，数字和的最大值。

输入：第一行是行数r（1≤r≤1000），后面r行是数字三角形的每一行（每个数字 0~100）；

输出：最大路径和。

示例输入：

5
7
3 8
8 1 0
2 7 4 4
4 5 2 6 5

示例输出：30（路径：7→3→8→7→5）

思路拆解（四步曲套用）

第一步：定义状态

数字三角形是二维结构，且路径方向固定（左下 / 右下），因此定义：dp[i][j] = 从顶端(1,1)走到第i行第j列时的最大路径和。

目标是求第r行所有**dp[r][j]**中的最大值（因为可以走到低端任意位置）。

第二步：推导状态转移方程

走到(i,j)的前一步只有两种可能：

1. 从上方(i-1,j)走下来（因为(i-1,j)的右下方是(i,j)）；
2. 从左上方(i-1,j-1)走下来（因为(i-1,j-1)的右下方是(i,j)）。

因此，dp[i][j] = 两种前序状态的最大值 + 当前位置的数字，即：dp[i][j] = max(dp[i-1][j], dp[i-1][j-1]) + a[i][j]

这里**a[i][j]**表示第i行第j列的数字。

第三步：初始化

• 顶端初始化：dp[1][1] = a[1][1]（起点只有一个，路径和就是自身）；
• 边界处理：第i行有i个数字，j的范围是1~i。对于j=1（每行第一个元素），只能从(i-1,1)走下来，所以dp[i][1] = dp[i-1][1] + a[i][1]；对于j=i（每行最后一个元素），只能从(i-1,i-1)走下来，所以dp[i][i] = dp[i-1][i-1] + a[i][i]。

第四步：填表顺序

从第 2 行开始，每行从左到右填表（因为dp[i][j]依赖dp[i-1][j]和dp[i-1][j-1]，上一行已计算完成）。

代码实现（基础版：二维数组）

#include <iostream>
#include <algorithm>
using namespace std;

const int N = 1010; // 因为r最大1000，数组开1010足够
int r;
int a[N][N]; // 存储数字三角形
int dp[N][N]; // dp[i][j]：走到(i,j)的最大路径和

int main() {
    cin >> r;
    // 读取数字三角形（注意：第i行有i个元素）
    for (int i = 1; i <= r; i++) {
        for (int j = 1; j <= i; j++) {
            cin >> a[i][j];
        }
    }

    // 初始化：顶端
    dp[1][1] = a[1][1];

    // 填表：从第2行到第r行
    for (int i = 2; i <= r; i++) {
        // 处理每行第一个元素（j=1）
        dp[i][1] = dp[i-1][1] + a[i][1];
        // 处理每行中间元素（2<=j<=i-1）
        for (int j = 2; j < i; j++) {
            dp[i][j] = max(dp[i-1][j], dp[i-1][j-1]) + a[i][j];
        }
        // 处理每行最后一个元素（j=i）
        dp[i][i] = dp[i-1][i-1] + a[i][i];
    }

    // 找第r行的最大值
    int max_sum = 0;
    for (int j = 1; j <= r; j++) {
        max_sum = max(max_sum, dp[r][j]);
    }

    cout << max_sum << endl;
    return 0;
}

优化：滚动数组（空间从 O (r²)→O (r)）

观察状态转移方程：**dp[i][j]只依赖上一行（i-1）的j和j-1位置，不需要存储所有行的dp值。因此可以用一维数组dp[j]**替代二维数组，通过 "从右向左" 填表避免覆盖前序状态。

优化后代码：

#include <iostream>
#include <algorithm>
using namespace std;

const int N = 1010;
int r;
int a[N][N];
int dp[N]; // 一维数组：dp[j]表示当前行第j列的最大路径和

int main() {
    cin >> r;
    for (int i = 1; i <= r; i++) {
        for (int j = 1; j <= i; j++) {
            cin >> a[i][j];
        }
    }

    // 初始化：第一行
    dp[1] = a[1][1];

    // 填表：从第2行开始，每行从右向左填
    for (int i = 2; i <= r; i++) {
        // 从右向左：避免dp[j-1]被覆盖（如果从左向右，dp[j]会覆盖dp[j-1]，影响后续计算）
        for (int j = i; j >= 1; j--) {
            if (j == 1) {
                // 每行第一个元素：只能从上方下来
                dp[j] = dp[j] + a[i][j];
            } else if (j == i) {
                // 每行最后一个元素：只能从左上方下来
                dp[j] = dp[j-1] + a[i][j];
            } else {
                // 中间元素：取上一行j和j-1的最大值
                dp[j] = max(dp[j], dp[j-1]) + a[i][j];
            }
        }
    }

    // 找最大值
    int max_sum = 0;
    for (int j = 1; j <= r; j++) {
        max_sum = max(max_sum, dp[j]);
    }

    cout << max_sum << endl;
    return 0;
}

优化解析

为什么要 "从右向左" 填表？因为一维数组**dp[j]**存储的是上一行的状态：

• 如果从左向右填，计算dp[j]时会覆盖dp[j-1]，而后续计算dp[j+1]需要上一行的dp[j]（已被覆盖），导致错误；
• 从右向左填时，dp[j]依赖的dp[j]（上一行的j）和dp[j-1]（上一行的j-1）都还没被覆盖，计算正确。

这种优化在矩阵规模较大时（如1e3×1e3）效果明显，能节省大量内存。

例题 2：矩阵的最小路径和（牛客 DP11）------ 路径类 DP 的 "导航基础题"

题目链接：https://www.nowcoder.com/practice/38ae72379d42471db1c537914b06d48e?tpId=230&tqId=39755&ru=/exam/o

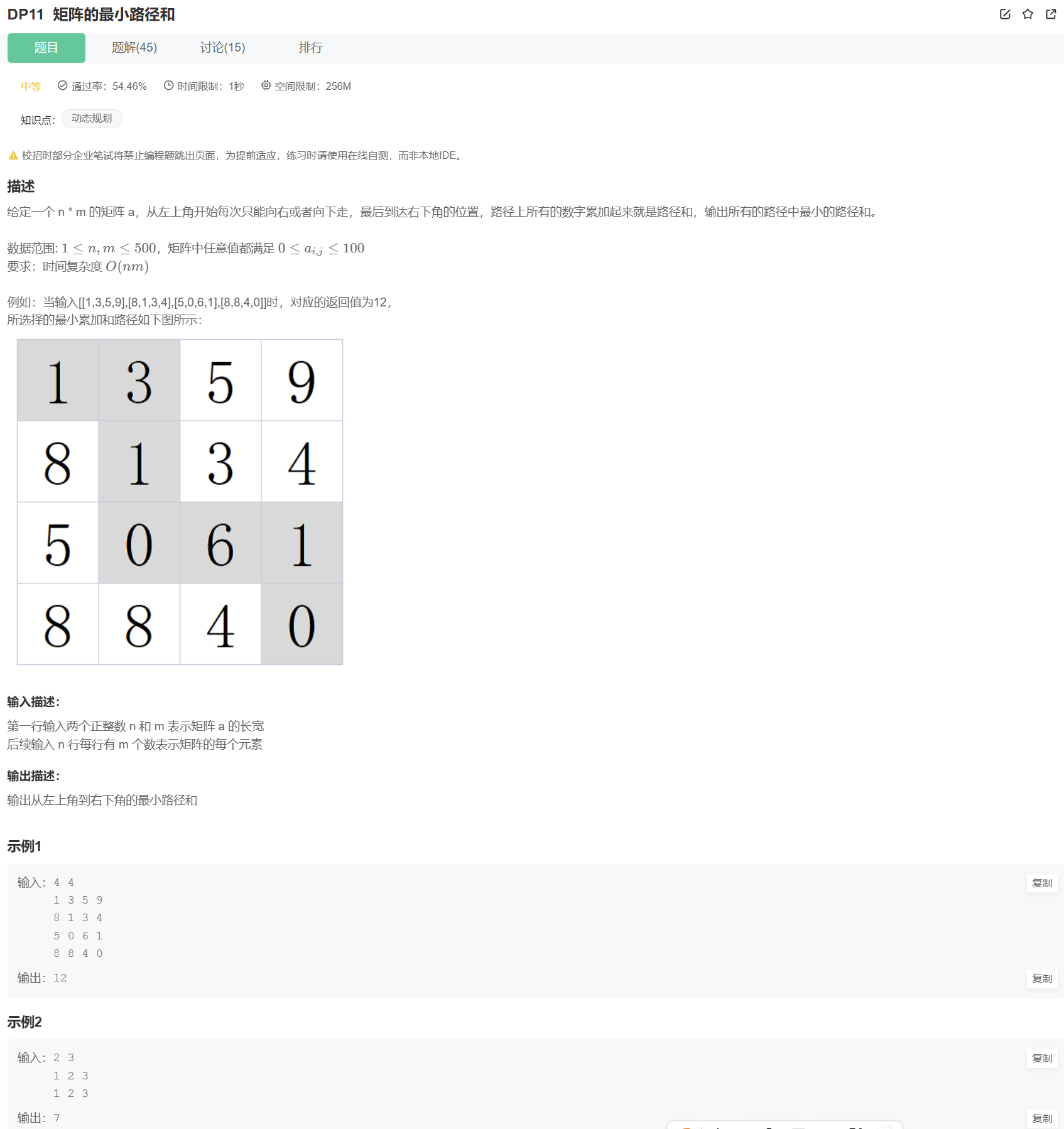
题目描述：从左上角到右下角的最小代价

给定一个n×m的矩阵，每次只能向右或向下走，求从左上角(1,1)到右下角(n,m)的路径上，所有数字的和的最小值。

输入：第一行是n和m（1≤n,m≤500），后面n行是矩阵元素（0≤a [i][j]≤100）；

输出：最小路径和。

示例输入：

4 4
1 3 5 9
8 1 3 4
5 0 6 1
8 8 4 0

示例输出：12（路径：1→3→1→0→6→1→0）

思路拆解（四步曲套用）

第一步：定义状态

矩阵路径问题，目标是 "最小路径和"，因此定义：dp[i][j] = 从(1,1)走到(i,j)的最小路径和。

目标是dp[n][m]（因为必须走到右下角）。

第二步：推导状态转移方程

只能向右或向下走，所以走到(i,j)的前一步只有两种可能：

1. 从上方(i-1,j)向下走：路径和 = dp[i-1][j] + a[i][j]；
2. 从左方(i,j-1)向右走：路径和 = dp[i][j-1] + a[i][j]。

要找最小值，因此转移方程：dp[i][j] = min(dp[i-1][j], dp[i][j-1]) + a[i][j]

第三步：初始化

需要处理第一行和第一列（边界）：

• 第一行：只能从左向右走，所以dp[1][j] = dp[1][j-1] + a[1][j]（比如dp[1][2] = dp[1][1] + a[1][2]，dp[1][3] = dp[1][2] + a[1][3]）；
• 第一列：只能从上向下走，所以dp[i][1] = dp[i-1][1] + a[i][1]；
• 起点：dp[1][1] = a[1][1]（初始状态）。

但这里有个小技巧：为了避免边界判断（比如i=1或j=1时的特殊处理），可以将dp数组的规模扩大一行一列（dp[0..n][0..m]），并将dp[0][1]或dp[1][0]初始化为 0，其他无效位置初始化为无穷大（0x3f3f3f3f），这样可以统一转移方程。

第四步：填表顺序

从左到右、从上到下（因为dp[i][j]依赖dp[i-1][j]（上一行已算完）和dp[i][j-1]（同一行左边已算完））。

代码实现（基础版：二维数组 + 边界优化）

#include <iostream>
#include <cstring> // 用于memset
#include <algorithm>
using namespace std;

const int N = 510; // n和m最大500，开510足够
int n, m;
int a[N][N]; // 存储矩阵
int dp[N][N]; // dp[i][j]：走到(i,j)的最小路径和

int main() {
    cin >> n >> m;
    // 读取矩阵
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= m; j++) {
            cin >> a[i][j];
        }
    }

    // 初始化：将dp数组填充为无穷大，避免无效状态干扰
    memset(dp, 0x3f, sizeof(dp));
    // 起点的前序状态：dp[0][1] = 0（或dp[1][0] = 0），保证dp[1][1]计算正确
    dp[0][1] = 0;

    // 填表：从左到右，从上到下
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= m; j++) {
            // 统一转移方程：不需要判断边界（因为dp[0][j]和dp[i][0]都是无穷大，不影响min结果）
            dp[i][j] = min(dp[i-1][j], dp[i][j-1]) + a[i][j];
        }
    }

    // 输出右下角的最小路径和
    cout << dp[n][m] << endl;
    return 0;
}

代码解析：为什么用 "无穷大" 初始化？

• 无效状态（如dp[0][j]、dp[i][0]）表示**"无法到达的位置"** ，它们的路径和应该是无穷大；
• 当计算第一行dp[1][j]时，dp[i-1][j] = dp[0][j] = 无穷大，所以min(无穷大, dp[1][j-1])会自动取dp[1][j-1]，符合 "第一行只能从左向右" 的逻辑；
• 同理，第一列dp[i][1]会自动取dp[i-1][1]，符合 "第一列只能从上向下" 的逻辑；
• 这种方式避免了单独写if (i==1)或if (j==1)的判断，代码更简洁。

优化：滚动数组（空间 O (nm)→O (m)）

观察转移方程：dp[i][j]只依赖上一行的dp[i-1][j]和同一行的dp[i][j-1]，因此可用一维数组**dp[j]**存储，每次更新时覆盖上一行的状态。

优化后代码：

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;

const int N = 510;
int n, m;
int a[N][N];
int dp[N]; // 一维数组：dp[j]表示当前行第j列的最小路径和

int main() {
    cin >> n >> m;
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= m; j++) {
            cin >> a[i][j];
        }
    }

    // 初始化：无穷大
    memset(dp, 0x3f, sizeof(dp));
    // 起点的前序状态：dp[0] = 0（因为第一行第一个元素dp[1] = min(dp[0], dp[0]) + a[1][1] = 0 + a[1][1]）
    dp[0] = 0;

    // 填表：逐行处理，每行从左到右
    for (int i = 1; i <= n; i++) {
        // 处理当前行的第一个元素（j=1）：只能从上一行的j=1下来
        dp[1] = dp[1] + a[i][1];
        // 处理当前行的其他元素（j>=2）
        for (int j = 2; j <= m; j++) {
            // dp[j]（上一行的j）和dp[j-1]（当前行的j-1）取min，加上当前元素
            dp[j] = min(dp[j], dp[j-1]) + a[i][j];
        }
    }

    cout << dp[m] << endl;
    return 0;
}

优化解析

• 逐行处理时，dp[j]初始存储的是上一行的dp[j]（即dp[i-1][j]）；
• 处理当前行j=1时，只能从上一行j=1下来，所以dp[1] = dp[1]（上一行） + a[i][1]；
• 处理j>=2时，dp[j] = min (上一行的dp[j]（未被覆盖）, 当前行的dp[j-1]（已计算）) + a [i][j]，逻辑正确；
• 空间从O(nm)降至O(m)，对于n=1e3、m=1e3的矩阵，内存占用从 1e6 降到 1e3，效果显著。

例题 3："木" 迷雾森林（牛客网）------ 路径类 DP 的 "障碍迷宫题"

题目链接：https://ac.nowcoder.com/acm/problem/53675

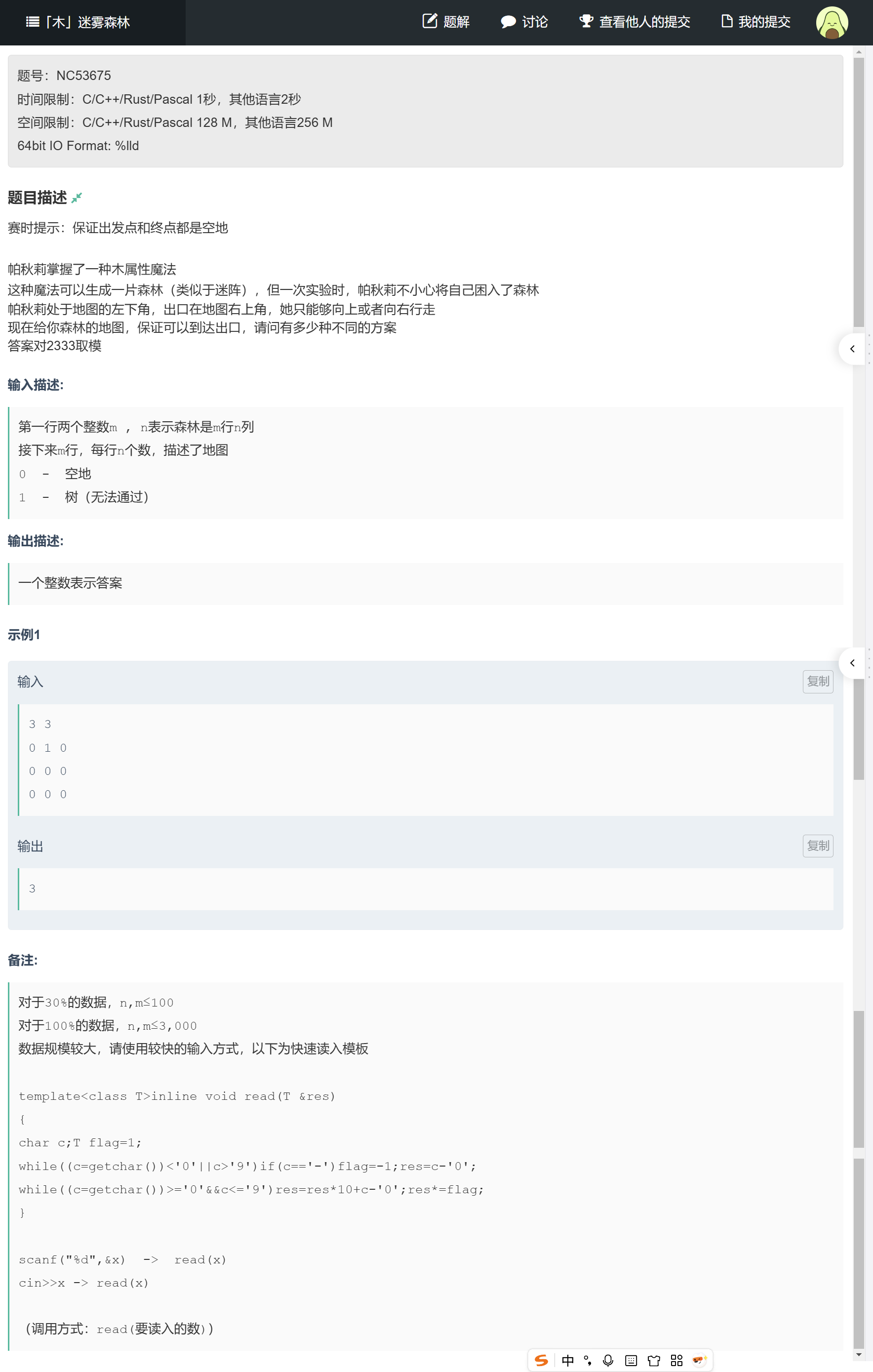
题目描述：从左下角到右上角的路径计数

帕秋莉被困在m行n列的森林迷宫里，起点在左下角(m,1)，出口在右上角(1,n)，每次只能向上或向右走。迷宫中有 "树"（标记为 1），无法通过；"空地"（标记为 0）可通过。求从起点到出口的不同路径数，结果对 2333 取模。

输入：第一行是m和n（1≤m,n≤3000），后面m行是迷宫矩阵（0 或 1）；

输出：路径数（对 2333 取模）。

示例输入：

3 3
0 1 0
0 0 0
0 0 0

示例输出：3（路径：(3,1)→(3,2)→(3,3)→(2,3)→(1,3)；(3,1)→(2,1)→(2,2)→(2,3)→(1,3)；(3,1)→(2,1)→(1,1)→(1,2)→(1,3)）

思路拆解（四步曲套用）

第一步：定义状态

迷宫路径计数问题，且有障碍，因此定义：dp[i][j] = 从起点(m,1)走到(i,j)的不同路径数（dp[i][j] = 0表示不可达）。

目标是dp[1][n]（出口位置）。

第二步：推导状态转移方程

只能向上或向右走，且只有空地（a[i][j] = 0）才能走：

1. 若**a[i][j] = 1**（树）：dp[i][j] = 0（不可达）；
2. 若**a[i][j] = 0** （空地）：走到(i,j)的前一步是(i+1,j)（从下方上来）或(i,j-1)（从左方过来），因此路径数是两者之和：dp[i][j] = (dp[i+1][j] + dp[i][j-1]) % 2333

第三步：初始化

起点是(m,1)（左下角），因此：

• dp[m][1] = 1（起点本身有 1 种路径：原地不动）；
• 为了避免边界判断（比如i=m时i+1越界，j=1时j-1越界），可以在矩阵下方加一行（i=m+1），左侧加一列（j=0），并将dp[m+1][1] = 0（下方无路径）、dp[m][0] = 0（左侧无路径），但更简单的方式是直接初始化dp[m][0] = 1（让dp[m][1] = dp[m+1][1]（0） + dp[m][0]（1） = 1）。

第四步：填表顺序

因为只能向上或向右走，且起点在(m,1)（下方），所以需要 "从下到上、从左到右" 填表：

• 从下到上：保证计算dp[i][j]时，dp[i+1][j]（下方）已计算；
• 从左到右：保证计算dp[i][j]时，dp[i][j-1]（左侧）已计算。

代码实现（基础版：二维数组）

#include <iostream>
using namespace std;

const int N = 3010; // m和n最大3000，开3010足够
const int MOD = 2333;
int m, n;
int a[N][N]; // 迷宫矩阵（1：树，0：空地）
int dp[N][N]; // dp[i][j]：走到(i,j)的路径数

int main() {
    // 读取输入（注意：题目中迷宫的行是m行，列是n列）
    scanf("%d%d", &m, &n); // 用scanf更快，避免超时
    for (int i = 1; i <= m; i++) {
        for (int j = 1; j <= n; j++) {
            scanf("%d", &a[i][j]);
        }
    }

    // 初始化：起点(m,1)的左侧dp[m][0] = 1，保证dp[m][1] = dp[m+1][1]（0） + dp[m][0]（1） = 1
    dp[m][0] = 1;

    // 填表：从下到上（i从m到1），从左到右（j从1到n）
    for (int i = m; i >= 1; i--) {
        for (int j = 1; j <= n; j++) {
            // 如果是树，路径数为0
            if (a[i][j] == 1) {
                dp[i][j] = 0;
            } else {
                // 路径数 = 下方路径数 + 左侧路径数（取模）
                dp[i][j] = (dp[i+1][j] + dp[i][j-1]) % MOD;
            }
        }
    }

    // 输出出口(1,n)的路径数
    printf("%d\n", dp[1][n]);
    return 0;
}

代码解析：为什么用scanf而不是cin？

因为m和n最大 3000，矩阵规模是3000×3000 = 9e6，cin默认速度较慢，可能导致超时；scanf速度更快，能避免超时问题（实际编程中，遇到大数据量时建议用scanf/printf）。

优化：滚动数组（空间 O (mn)→O (n)）

观察转移方程：dp[i][j]只依赖下方dp[i+1][j]（上一行的j）和左侧dp[i][j-1]（当前行的j-1），因此可用一维数组**dp[j]**存储，每次从下到上更新时，覆盖上一行的状态。

优化后代码：

#include <iostream>
using namespace std;

const int N = 3010;
const int MOD = 2333;
int m, n;
int a[N][N];
int dp[N]; // 一维数组：dp[j]表示当前行第j列的路径数

int main() {
    scanf("%d%d", &m, &n);
    for (int i = 1; i <= m; i++) {
        for (int j = 1; j <= n; j++) {
            scanf("%d", &a[i][j]);
        }
    }

    // 初始化：起点(m,1)的左侧dp[0] = 1
    dp[0] = 1;

    // 填表：从下到上（i从m到1），每行从左到右
    for (int i = m; i >= 1; i--) {
        // 处理当前行的第一个元素（j=1）
        if (a[i][1] == 1) {
            dp[1] = 0;
        } else {
            // 只能从下方（上一行的dp[1]）过来
            dp[1] = dp[1] % MOD;
        }

        // 处理当前行的其他元素（j>=2）
        for (int j = 2; j <= n; j++) {
            if (a[i][j] == 1) {
                dp[j] = 0;
            } else {
                // dp[j]（上一行的j，即下方路径数） + dp[j-1]（当前行的j-1，即左侧路径数）
                dp[j] = (dp[j] + dp[j-1]) % MOD;
            }
        }
    }

    printf("%d\n", dp[n]);
    return 0;
}

优化解析

• 从下到上处理每行时，dp[j]初始存储的是下一行（i+1）的dp[j]（即下方路径数）；
• 处理当前行j=1时，只能从下方过来，所以dp[1] = 下一行的dp[1]（若为树则置 0）；
• 处理j>=2时，dp[j] = 下一行的dp[j]（下方） + 当前行的dp[j-1]（左侧），取模后更新；
• 空间从O(mn)降至O(n)，对于m=3e3、n=3e3的矩阵，内存占用从 9e6 降到 3e3，极大节省资源。

例题 4：过河卒（洛谷 P1002）------ 路径类 DP 的 "障碍 + 特殊约束题"

题目链接：https://www.luogu.com.cn/problem/P1002

题目描述：卒避马的路径计数

棋盘上A点（0,0）有一个过河卒，要走到B点（n,m），每次只能向下或向右走。棋盘上C点（x,y）有一匹马，马所在的点和马跳跃一步可达的点（共 9 个点）是 "控制点"，卒不能经过。求卒从A到B的不同路径数。

输入：一行四个整数n, m, x, y（1≤n,m≤20，0≤x,y≤20）；

输出：路径数。

示例输入：

6 6 3 3

示例输出：6（马在 (3,3)，控制点覆盖周围 8 个点，卒需绕路走）

思路拆解（四步曲套用）

第一步：定义状态

卒的路径计数问题，且有 "马的控制点" 障碍，因此定义：dp[i][j] = 从(0,0)走到(i,j)的不同路径数（若(i,j)是控制点或越界，dp[i][j] = 0）。

目标是dp[n][m]。

第二步：推导状态转移方程

只能向下或向右走，且(i,j)必须不是控制点：

1. 若(i,j)是控制点：dp[i][j] = 0；
2. 若(i,j)不是控制点：走到(i,j)的前一步是(i-1,j)（上方）或(i,j-1)（左侧），因此路径数是两者之和：dp[i][j] = dp[i-1][j] + dp[i][j-1]

第三步：初始化

• 起点(0,0) ：若不是控制点，dp[0][0] = 1；若被马控制（比如马在 (0,0)），dp[0][0] = 0；
• 边界处理 ：第一行（i=0）只能从左向右走，若(0,j)不是控制点，dp[0][j] = dp[0][j-1]；第一列（j=0）只能从上向下走，若(0,j)不是控制点，dp[i][0] = dp[i-1][0]；
• 马的控制点：需要先标记出所有控制点（马的位置(x,y) + 马跳一步的 8 个位置：(x±2,y±1)、(x±1,y±2)）。

第四步：填表顺序

从左到右、从上到下（因为dp[i][j]依赖dp[i-1][j]（上一行）和dp[i][j-1]（左侧））。

代码实现（基础版：二维数组 + 控制点标记）

#include <iostream>
#include <cmath> // 用于abs函数
using namespace std;

typedef long long LL; // 路径数可能很大，用long long避免溢出
const int N = 25; // n和m最大20，开25足够
int n, m, x, y;
LL dp[N][N]; // dp[i][j]：走到(i,j)的路径数

// 判断(i,j)是否是马的控制点
bool is_control(int i, int j) {
    // 马的位置：(x,y)
    if (i == x && j == y) return true;
    // 马跳一步的8个位置：dx和dy的组合是(±2,±1)、(±1,±2)
    int dx = abs(i - x);
    int dy = abs(j - y);
    return (dx == 2 && dy == 1) || (dx == 1 && dy == 2);
}

int main() {
    cin >> n >> m >> x >> y;

    // 初始化：起点(0,0)
    if (!is_control(0, 0)) {
        dp[0][0] = 1;
    } else {
        dp[0][0] = 0;
    }

    // 初始化第一行（i=0，j从1到m）
    for (int j = 1; j <= m; j++) {
        if (!is_control(0, j)) {
            dp[0][j] = dp[0][j-1]; // 只能从左向右
        } else {
            dp[0][j] = 0;
        }
    }

    // 初始化第一列（j=0，i从1到n）
    for (int i = 1; i <= n; i++) {
        if (!is_control(i, 0)) {
            dp[i][0] = dp[i-1][0]; // 只能从上向下
        } else {
            dp[i][0] = 0;
        }
    }

    // 填表：从左到右，从上到下
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= m; j++) {
            if (is_control(i, j)) {
                dp[i][j] = 0;
            } else {
                dp[i][j] = dp[i-1][j] + dp[i][j-1];
            }
        }
    }

    cout << dp[n][m] << endl;
    return 0;
}

代码解析：为什么用long long？

当n和m为 20 时，最大路径数是C(40,20) ≈ 137846528820，远超int的最大值（约 2e9），因此必须用long long存储，避免溢出。

优化：边界统一处理（避免单独初始化第一行 / 列）

和 "矩阵最小路径和" 类似，我们可以将dp数组的规模扩大一行一列（dp[0..n+1][0..m+1]），并将dp[1][0] = 1（起点(0,0)对应dp[1][1]），这样可以统一转移方程，不需要单独初始化第一行和第一列。

优化后代码：

#include <iostream>
#include <cmath>
using namespace std;

typedef long long LL;
const int N = 25;
int n, m, x, y;
LL dp[N][N];

bool is_control(int i, int j) {
    // 注意：这里i和j是扩大后的坐标，需要减1对应原坐标
    i--; j--;
    if (i == x && j == y) return true;
    int dx = abs(i - x);
    int dy = abs(j - y);
    return (dx == 2 && dy == 1) || (dx == 1 && dy == 2);
}

int main() {
    cin >> n >> m >> x >> y;

    // 扩大坐标：原(0,0)对应(1,1)，dp[1][0] = 1（前序状态）
    dp[1][0] = 1;

    // 填表：从左到右，从上到下（i从1到n+1，j从1到m+1）
    for (int i = 1; i <= n+1; i++) {
        for (int j = 1; j <= m+1; j++) {
            // 跳过起点的前序状态（i=1,j=0已处理）
            if (i == 1 && j == 0) continue;
            // 判断当前扩大后的坐标是否是控制点
            if (is_control(i, j)) {
                dp[i][j] = 0;
            } else {
                // 统一转移方程：dp[i-1][j]（上方） + dp[i][j-1]（左侧）
                dp[i][j] = dp[i-1][j] + dp[i][j-1];
            }
        }
    }

    // 原(n,m)对应扩大后的(n+1,m+1)
    cout << dp[n+1][m+1] << endl;
    return 0;
}

优化解析

• 扩大坐标后，原坐标(i,j)对应新坐标(i+1,j+1)，这样可以避免i=0或j=0时的越界判断；
• dp[1][0] = 1：保证新坐标(1,1)（原(0,0)）的路径数为dp[0][1]（0） + dp[1][0]（1） = 1；
• 统一转移方程后，不需要单独初始化第一行和第一列，代码更简洁。

三、路径类 DP 通用解题模板总结

通过以上 4 道例题，我们可以总结出路径类 DP 的通用解题模板，以后遇到这类题，直接套用即可：

1. 问题分析

• 确定地图结构：是二维矩阵、三角形、还是迷宫？
• 确定移动方向：只能向右 / 向下 / 向上 / 向左，或多方向？
• 确定目标：求最小 / 最大路径和、路径数，还是带约束的路径？
• 确定障碍：是否有不可达区域（如树、马的控制点）？

2. 状态定义

• 二维状态：dp[i][j] = 走到(i,j)的目标值（路径和 / 路径数）；
• 一维状态（优化后）：dp[j] = 当前行第j列的目标值。

3. 转移方程推导

• 无障碍 + 单方向（右 / 下）：dp[i][j] = min/max/sum(dp[i-1][j], dp[i][j-1]) + 权重（如矩阵元素）；
• 有障碍：先判断(i,j)是否可达，可达则按无障碍推导，不可达则dp[i][j] = 0（计数）或无穷大（最值）；
• 多方向（上 / 右）：调整填表顺序（如从下到上），确保依赖的前序状态已计算。

4. 初始化

• 起点初始化 ：dp[起点坐标] = 1（计数）或起点权重（路径和）；
• 边界初始化：第一行 / 列按移动方向单独初始化，或扩大数组规模统一处理；
• 障碍初始化：标记所有不可达区域，初始化为 0 或无穷大。

5. 填表顺序

• 右 / 下方向：从左到右、从上到下；
• 上 / 右方向：从下到上、从左到右；
• 优化版（一维数组）：根据依赖关系确定遍历方向（如从右向左避免覆盖）。

6. 优化技巧

• 空间优化：用一维数组替代二维数组（滚动数组），空间复杂度从O(nm)降至O(m)；
• 时间优化：提前标记障碍，避免填表时重复判断；用scanf/printf处理大数据量；
• 边界优化：扩大数组规模，统一转移方程，避免单独处理第一行 / 列。

---

总结

路径类 DP 作为线性 DP 的重要分支，本质是 "用位置定义状态，用方向推导转移"。它的难点不在于逻辑复杂，而在于 "状态设计的合理性" 和 "边界处理的严谨性"------ 比如如何定义dp[i][j]才能让转移方程自然成立，如何处理障碍和越界避免逻辑漏洞。

最后，给大家一个小建议：刷题时不要急于看题解，先尝试自己套用 "四步曲"------ 先定义状态，再推导转移方程，最后写代码验证。遇到错误时，先检查状态定义是否合理，再看转移方程是否覆盖所有情况，最后排查边界和填表顺序。

路径类 DP 是后续学习更复杂 DP（如区间 DP、树形 DP）的基础，打好这个基础，后面的学习会事半功倍。希望这篇 5000 字的保姆级教程，能帮你彻底吃透路径类线性 DP，在算法路上更上一层楼！