回溯算法专题(九)：棋盘上的巅峰对决——经典「N 皇后」问题

哈喽各位，我是前端小L。

欢迎来到我们的回溯算法专题第九篇！

这就是传说中的 N 皇后问题。

规则很简单：在一个 N x N 的棋盘上放置 N 个皇后，使得它们不能互相攻击。

皇后攻击范围：同一行、同一列、同一条斜线（45度或135度）。

这就意味着：每一行、每一列、每一条斜线上，最多只能有一个皇后。

力扣 51. N 皇后

https://leetcode.cn/problems/n-queens/

题目分析：

输入：整数 n。
目标：返回所有合法的 N 皇后摆放方案。
输出：用 '.' 表示空，'Q' 表示皇后。

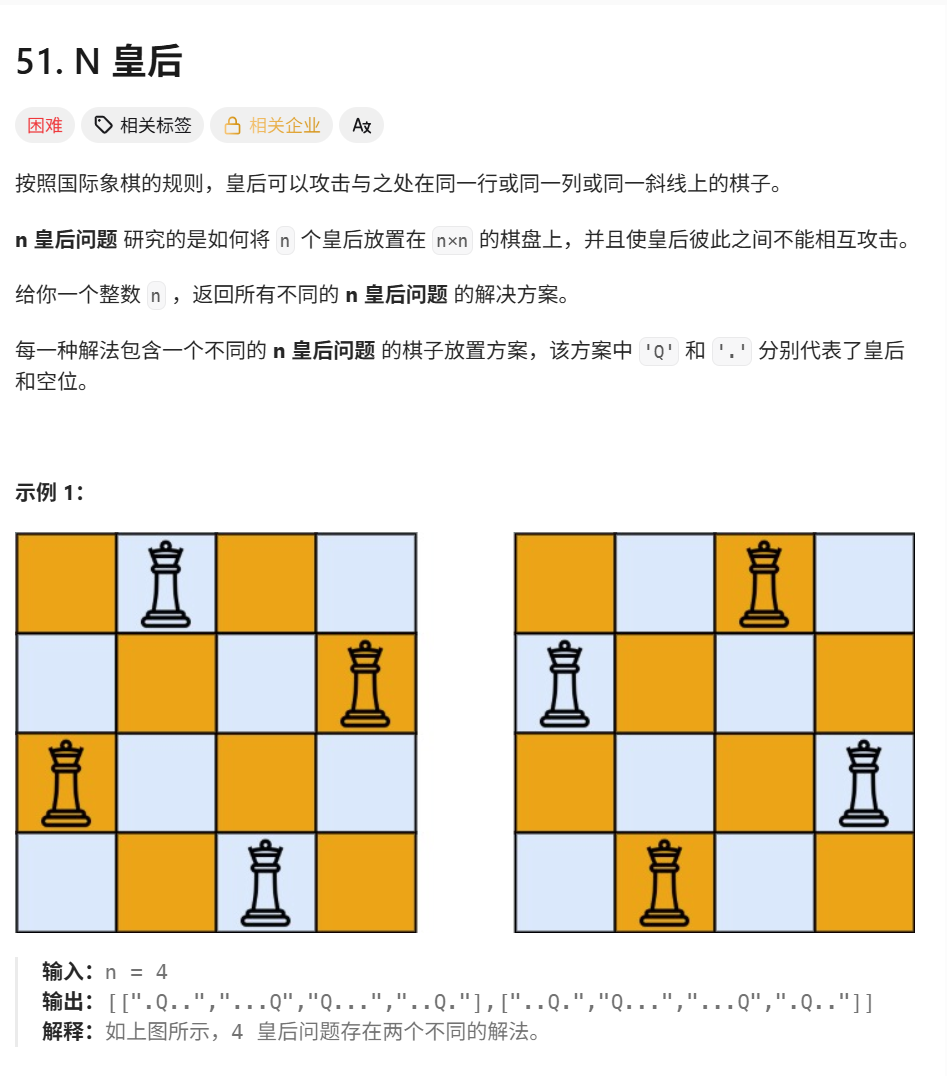
例子： n = 4

方案1：
复制代码
```
.Q..
...Q
Q...
..Q.
```
方案2：
复制代码
```
..Q.
Q...
...Q
.Q..
```

核心思维：把二维降维打击

虽然是二维棋盘，但我们不需要在每一个格子都做"放或不放"的决策（那是 $2\^{N\^2}$ 复杂度，爆炸了）。

利用规则："每一行只能有一个皇后"。

这直接把决策树简化了：

树的深度 ：第 row 层决策，负责在第 row 行放置皇后。
树的分支 ：在当前行，我有 N 列可以选择。

isValid 的几何判定

当我们尝试在 (row, col) 放置皇后时，我们需要检查它是否安全。

因为我们是从上往下（row 从 0 到 N-1）放的，所以下面的行还没放，不用管。我们只需要检查**"上半区"**：

正上方 (列) ：col 这一列有没有皇后？
左上方 (45度) ：(row-1, col-1), (row-2, col-2)... 有没有皇后？
右上方 (135度) ：(row-1, col+1), (row-2, col+2)... 有没有皇后？
(不需要检查同一行，因为我们每行只放一个，放完就进递归下一行了)

算法流程

初始化棋盘：
- vector<string> board(n, string(n, '.'))。
backtrack(row)：
- Base Case ：如果 row == n，说明 0 到 n-1 行都放好了，收集结果，返回。
- 遍历列 ：for col 从 0 到 n-1：
  - 检查合法性 ：isValid(row, col, board)。
  - 做选择 ：board[row][col] = 'Q'。
  - 递归：backtrack(row + 1)。
  - 撤销选择 ：board[row][col] = '.'。
isValid 函数实现细节：
- 只需要写三个 for 循环（或 while），分别向上、向左上、向右上扫描即可。

代码实现 (C++)

C++

复制代码

#include <vector>
#include <string>

using namespace std;

class Solution {
private:
    vector<vector<string>> res;

    // 检查在 (row, col) 放置皇后是否合法
    bool isValid(int row, int col, vector<string>& board, int n) {
        // 1. 检查正上方（列）
        for (int i = 0; i < row; ++i) {
            if (board[i][col] == 'Q') {
                return false;
            }
        }

        // 2. 检查左上方 (45度对角线)
        for (int i = row - 1, j = col - 1; i >= 0 && j >= 0; --i, --j) {
            if (board[i][j] == 'Q') {
                return false;
            }
        }

        // 3. 检查右上方 (135度对角线)
        for (int i = row - 1, j = col + 1; i >= 0 && j < n; --i, ++j) {
            if (board[i][j] == 'Q') {
                return false;
            }
        }

        // 不需要检查当前行，因为我们每行只放一个
        return true;
    }

    void backtrack(int n, int row, vector<string>& board) {
        // Base Case: 放到第 n 行（下标 n），说明 0~(n-1) 行都放好了
        if (row == n) {
            res.push_back(board);
            return;
        }

        // 尝试当前行的每一列
        for (int col = 0; col < n; ++col) {
            if (isValid(row, col, board, n)) {
                // 做选择
                board[row][col] = 'Q';
                
                // 进入下一行
                backtrack(n, row + 1, board);
                
                // 撤销选择
                board[row][col] = '.';
            }
        }
    }

public:
    vector<vector<string>> solveNQueens(int n) {
        res.clear();
        // 初始化空棋盘
        vector<string> board(n, string(n, '.'));
        
        backtrack(n, 0, board);
        
        return res;
    }
};

进阶优化：空间换时间

isValid 函数每次都要扫描棋盘，时间复杂度是 $O(N)$ 。有没有 $O(1)$ 的检查方法？

当然有！我们可以用三个布尔数组（或哈希表）来记录哪些列、哪些斜线被占用了。

cols[col]: 记录第 col 列是否占用。
diag1: 记录左上-右下斜线。
- 规律：同一条该方向斜线上的格子，row - col 是常数。
diag2: 记录右上-左下斜线。
- 规律：同一条该方向斜线上的格子，row + col 是常数。

这样 isValid 就变成了查表操作。虽然这道题 N 很小（N<=9），优化不明显，但这是一个很好的思维扩展。

深度复杂度分析

时间复杂度：O(N!)
- 第一行有 N 种选法，第二行最多 N-1 种，第三行 N-2 种...
- 实际上由于斜线限制，分支数远小于 N，但上限依然是阶乘级。
空间复杂度：O(N^2)
- 存储棋盘的空间。递归栈深度为 N。

总结：回溯的"格局"打开了

今天这道题，让我们从一维的"选数"，跨越到了二维的"布局"。

N 皇后问题的核心在于**"约束传播"**：你在第一行放下的一个棋子，会像发射激光一样，封锁住后面所有行的某些位置。

回溯算法在这里展现了它最强大的一面：在复杂的约束网中，自动寻找那条唯一的（或所有的）生路。

下一篇，我们将挑战回溯算法的终极应用，也是比 N 皇后更难、更贴近生活的棋盘游戏------解数独。

N 皇后是一行放一个，数独是每个格子都要填，而且有行、列、九宫格三重限制。

准备好迎接**"二维回溯"**的完全体了吗？

下期见！