文章目录
前言
摘要:本文详细介绍了希尔排序算法的实现原理和性能分析。文章首先阐述了希尔排序通过分组插入排序逐步逼近全局有序的核心思想,给出了具体实现步骤和代码示例。在性能分析部分,指出其空间复杂度为O(1),时间复杂度取决于增量序列选择,最坏情况下为O(n²),平均可达O(n^1.3)。最后总结了希尔排序不稳定、仅适用于顺序表的特点,并提供了知识要点回顾。全文通过图示和代码示例直观展示了希尔排序的分组排序过程,对理解这一经典排序算法具有重要参考价值。
一.思路
1.总体思想
- 对于直接插入排序的时间复杂度,有以下规律:
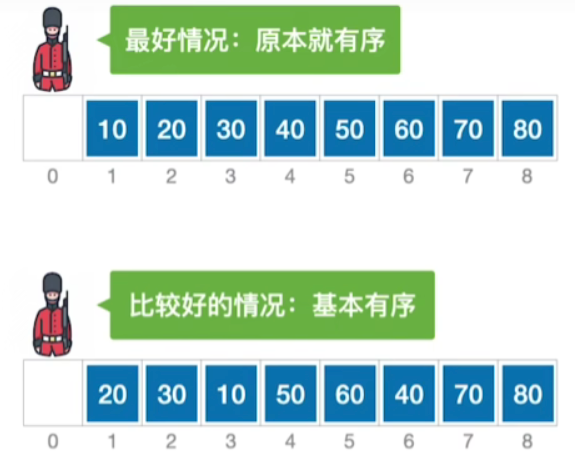
- 因此希尔排序是通过插入排序先追求表中元素部分有序,再逐渐逼近全局有序
2.实现思路
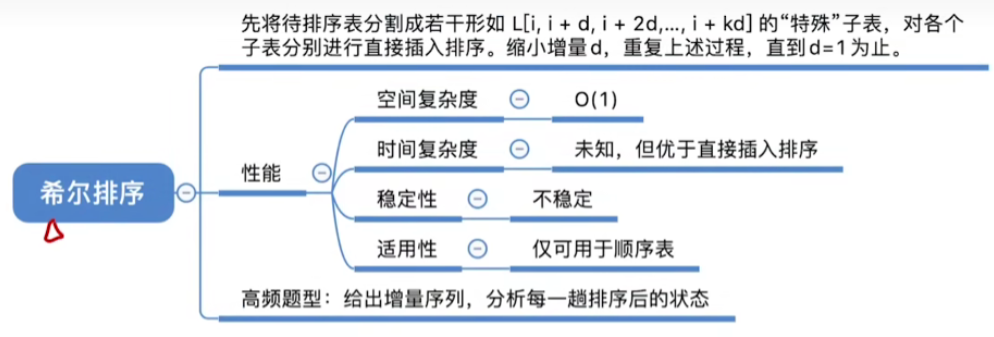
- 先将待排序表分割成若干形如 L [ i , i + d , i + 2 d , . . . , i + k d ] L[i,i+d,i+2d,...,i+kd] L[i,i+d,i+2d,...,i+kd]的"特殊"子表,对各个子表分别进行直接插入排序。缩小增量d,重复上述过程,直到d=1为止。
- 希尔本人建议:每次将增量缩小一半
3.具体例子
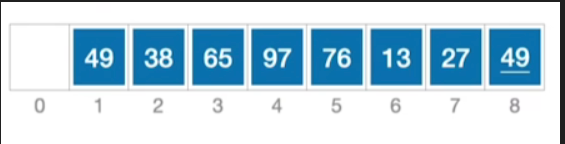
-
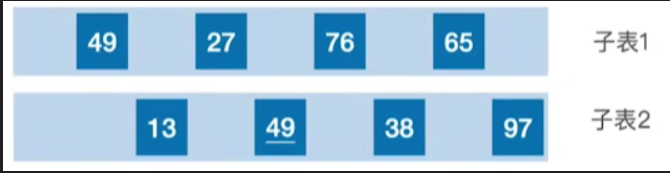
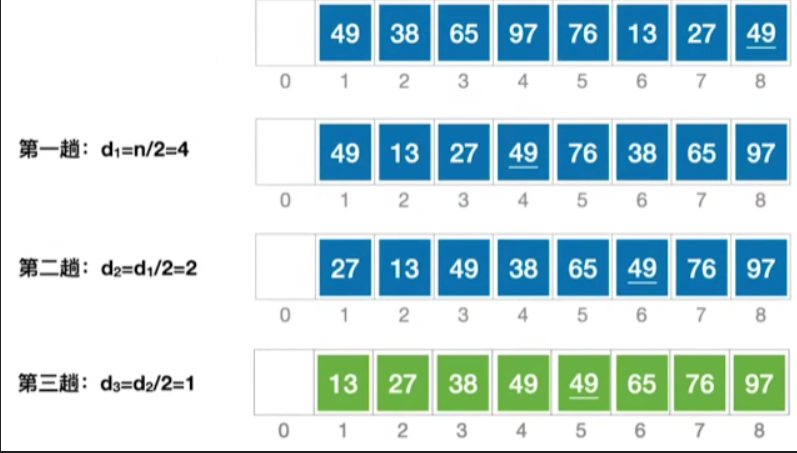
假设我们第一趟的排序,设定这个增量 d 1 = n / 2 = 4 d_1 = n / 2 = 4 d1=n/2=4,所有的相距距离为d的这些元素我们都会把它看作是属于同一个子表的元素,如:49和76;38和13,列出所有子表如下:
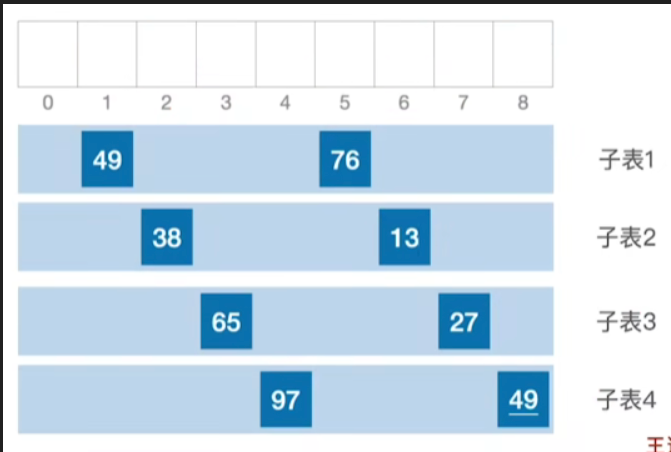
-
对各个子表分别进行直接插入排序
- 子表1:元素本就有序,直接插入排序元素顺序不变

- 子表2:38>13,因此,进行直接插入排序后,相当于交换两个元素的位置

- 子表3:65>27,直接插入排序后,相当于交换两个元素的位置

- 子表4:97>49,直接插入排序后,相当于交换两个元素的位置

- 子表1:元素本就有序,直接插入排序元素顺序不变
-
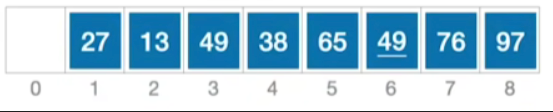
至此完成第一趟的排序,此时数组中各个元素的位置如下
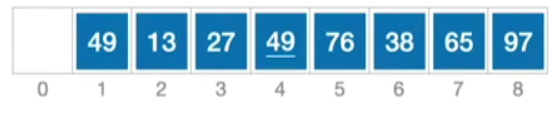
-
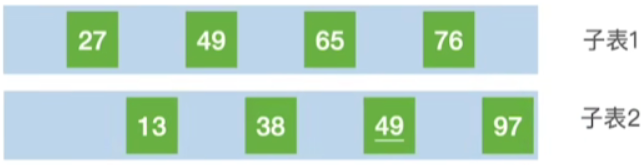
第二趟的处理我们会缩小这个增量d的值, d 2 = d 1 / 2 = 2 d_2 = d_1 / 2 = 2 d2=d1/2=2,因此第二趟的处理当中,我们会把相距距离为2的那些元素划分为同一个子表,如:49,27,76和65为同一个子表
-
分别对这几个子表进行插入排序
-
经过调整后表中元素如下
-
接下来再缩小d的值, d 3 = d 2 / 2 = 1 d_3 = d_2 / 2 = 1 d3=d2/2=1,此时相当与对整个数组进行插入排序.(整个表已呈现出"基本有序 ",对整体再进行一次"直接插入排序",由此可降低直接插入排序的时间复杂度)

-
总体过程如下:
二.具体算法代码实现
c
// 希尔排序
void ShellSort(int A[], int n) {
int d, i, j;
// A[0] 只是暂存单元,不是哨兵,当 j<=0 时,插入位置已到
for(d=n; d>=1; d=d/2) // 步长变化
for(i=d+1; i<n; i++i)
if(A[i]<A[i-d]) // 需将 A[i] 插入有序增量子表
A[0]=A[i]; // 暂存在 A[0]
for(j=i-d; j>0 && A[0]<A[j]; j=-d)
A[j+d]=A[j]; // 记录后移,查找插入的位置
A[j+d]=A[0]; // 插入
}// 1f
}- 初始时i指向的是d+1,也就是76(子表的第二个元素),这是因为在直接插入排序中元素是从数组的第二个元素开始检查是否需要插入

- 当遇到需要插入的元素时
- 需要先将其暂存到0号地址,然后将元素移动到i或者说j+d这个位置,如13

- 接下来满足j-d小于0的条件,因此跳出循环,将13插入到新位置
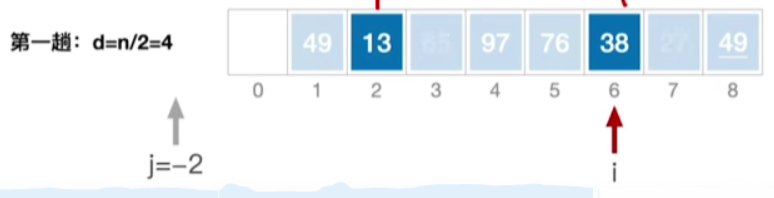
- 需要先将其暂存到0号地址,然后将元素移动到i或者说j+d这个位置,如13
- 值得注意的是:这里的算法思路在处理第二趟的元素时和我们的之直接插入排序略有不同
- i= d + 1 = 3
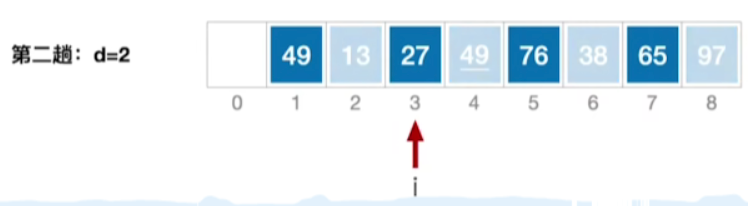
- 27 < 49,因此直接插入排序

- 按照我们之前的逻辑,接下来我们应处理的是i+d也是是5这个地址的元素,但是在这里的实现代码中,是直接执行的i++,这就使得我们处理的并不是当前子表的下一个元素,而是另外一个子表的第二个元素

- 49 > 13,无需调整,接下来还是i++,这就又切换到了之前处理的那个子表,只不过处理的是之前那个子表的第三个元素
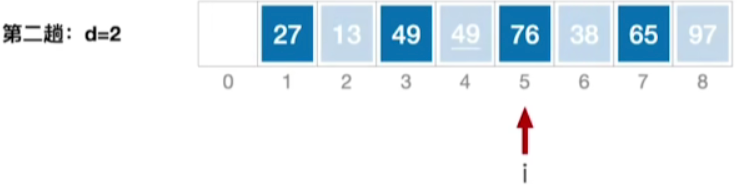
- 接下来的步骤也是类似,不再赘述
- i= d + 1 = 3
三.算法性能分析
1.空间复杂度
- O(1)
2.时间复杂度
- 采用不同的增量序列的时候,我们排序的趟数会受到影响,同时在每一趟排序当中各个元素的对比次数和移动次数也都会受到影响
- 时间复杂度:和增量序列d₁,d₂,d₃...的选择有关,目前无法用数学手段证明确切的时间复杂度最坏时间复杂度为O(n²),当n在某个范围内时,可达 O ( n 1.3 ) O(n^{1.3}) O(n1.3)
3.稳定性

- 不稳定
4.适用性
- 仅适用于顺序表,不适用于链表
四.知识回顾与重要考点
结语
六更😉
如果想查看更多章节,请点击:一、数据结构专栏导航页