平面图形的面积
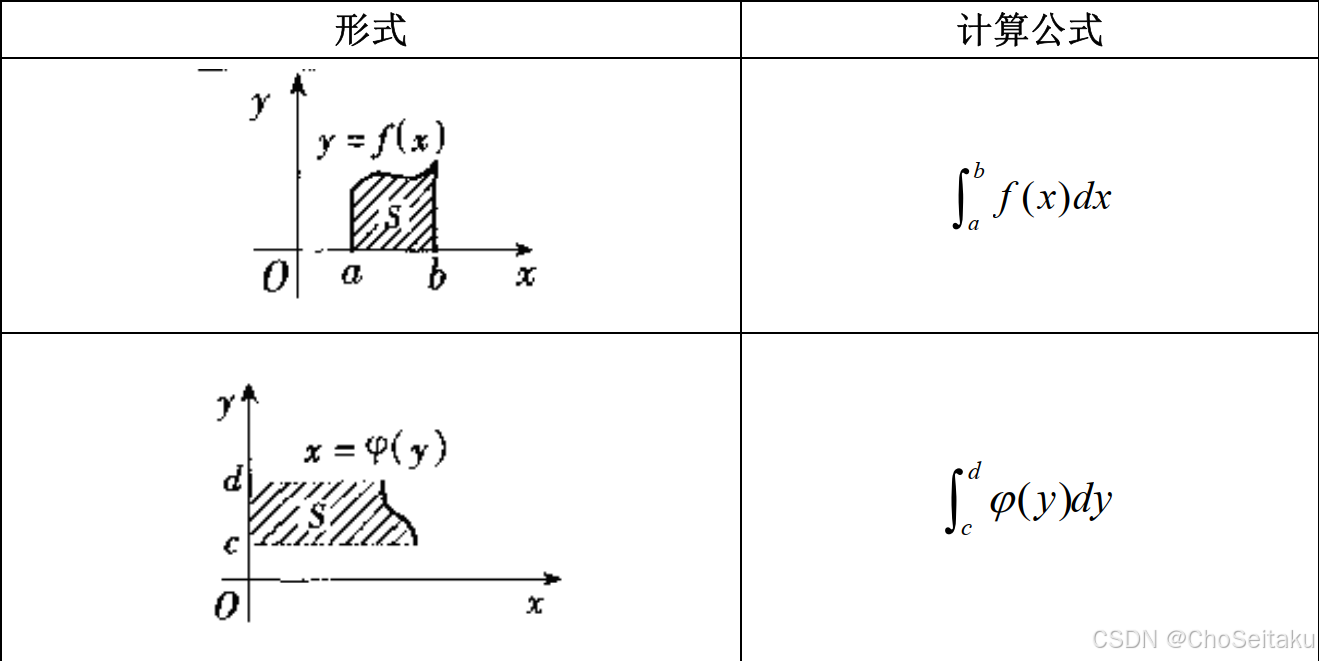
直角坐标系下平面图形的面积

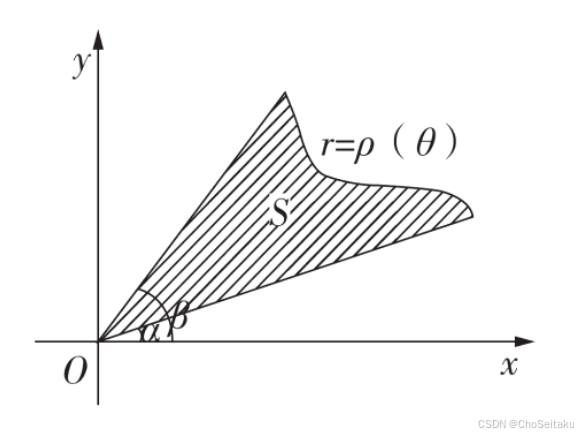
极坐标系下平面图形的面积
在极坐标系下,由直线θ=α和θ=β和曲线r=ρ(θ)所围图形的面积为S=12∫αβρ2(θ)dθ. \begin{aligned} &\text{在极坐标系下,由直线} \theta = \alpha \text{和} \theta = \beta \text{和} \\ &\text{曲线} r = \rho(\theta) \text{所围图形的面积为} \\ \\ &S = \frac{1}{2}\int_{\alpha}^{\beta} \rho^2(\theta)d\theta. \end{aligned} 在极坐标系下,由直线θ=α和θ=β和曲线r=ρ(θ)所围图形的面积为S=21∫αβρ2(θ)dθ.
参数方程下平面图形的面积
【小结】(1)曲线{x=x(t)y=y(t)与直线x=a,x=b所围成的阴影部分的面积S=∫x−1(a)x−1(b)y(t)x′(t)dt. \begin{aligned} &\text{【小结】(1)曲线} \begin{cases} x = x(t) \\ y = y(t) \end{cases} \text{与直线} x=a,x=b \text{所围成的阴影部分的面积} \\ &S = \int_{x^{-1}(a)}^{x^{-1}(b)} y(t)x'(t)dt . \end{aligned} 【小结】(1)曲线{x=x(t)y=y(t)与直线x=a,x=b所围成的阴影部分的面积S=∫x−1(a)x−1(b)y(t)x′(t)dt.
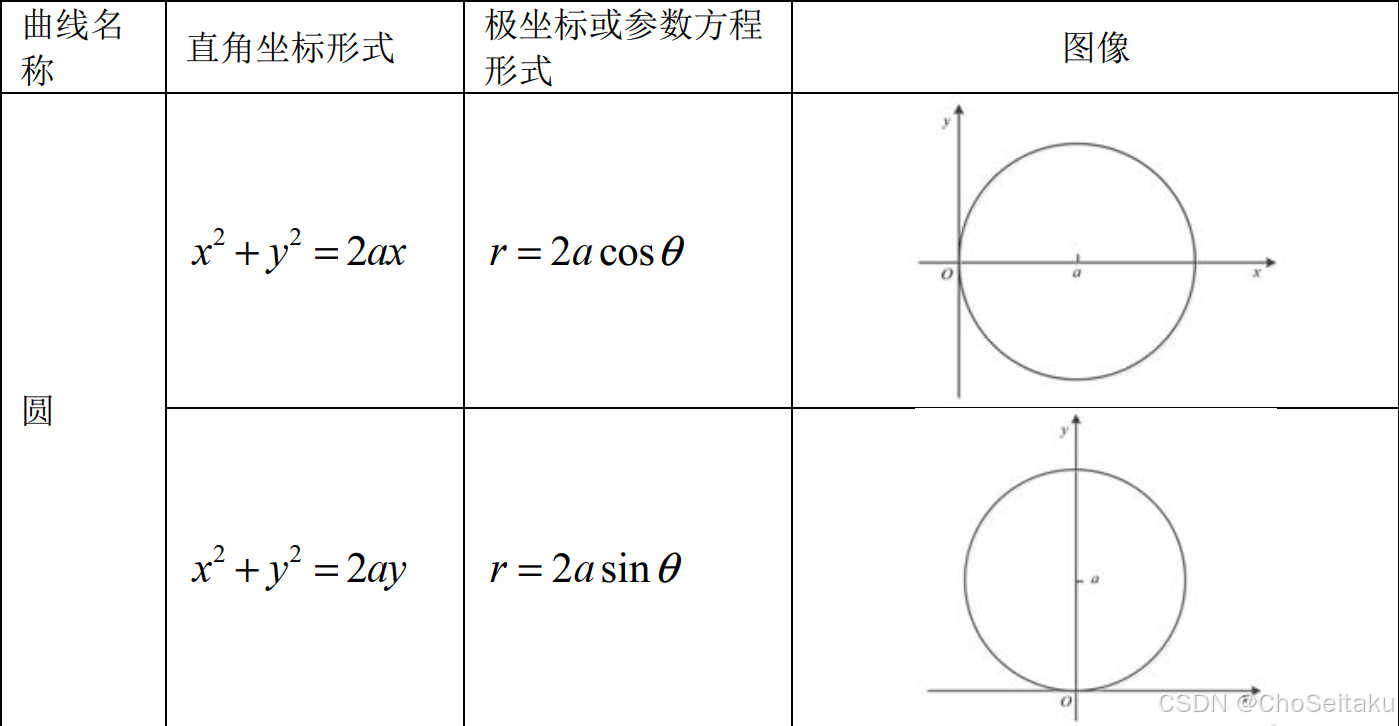
常见曲线的极坐标方程及其图像
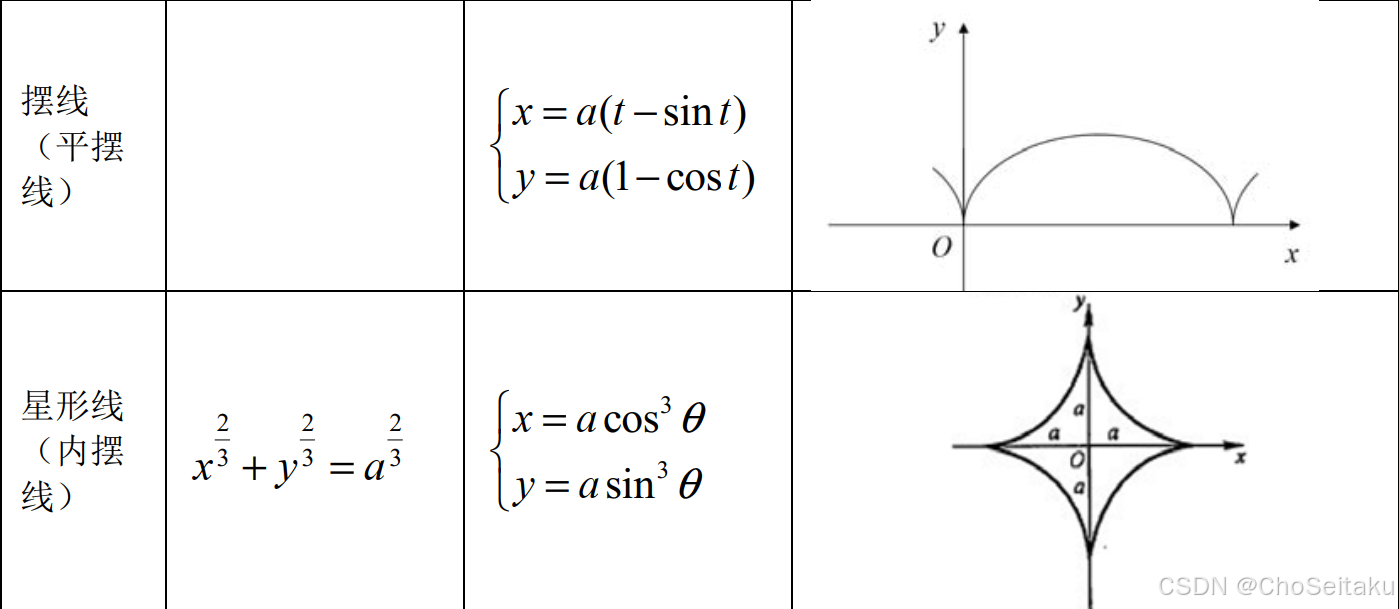
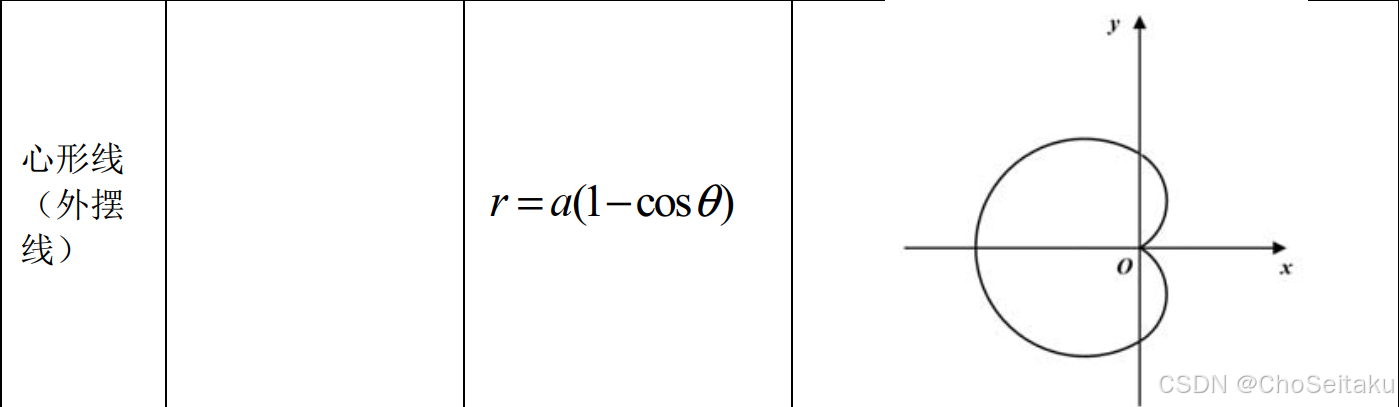
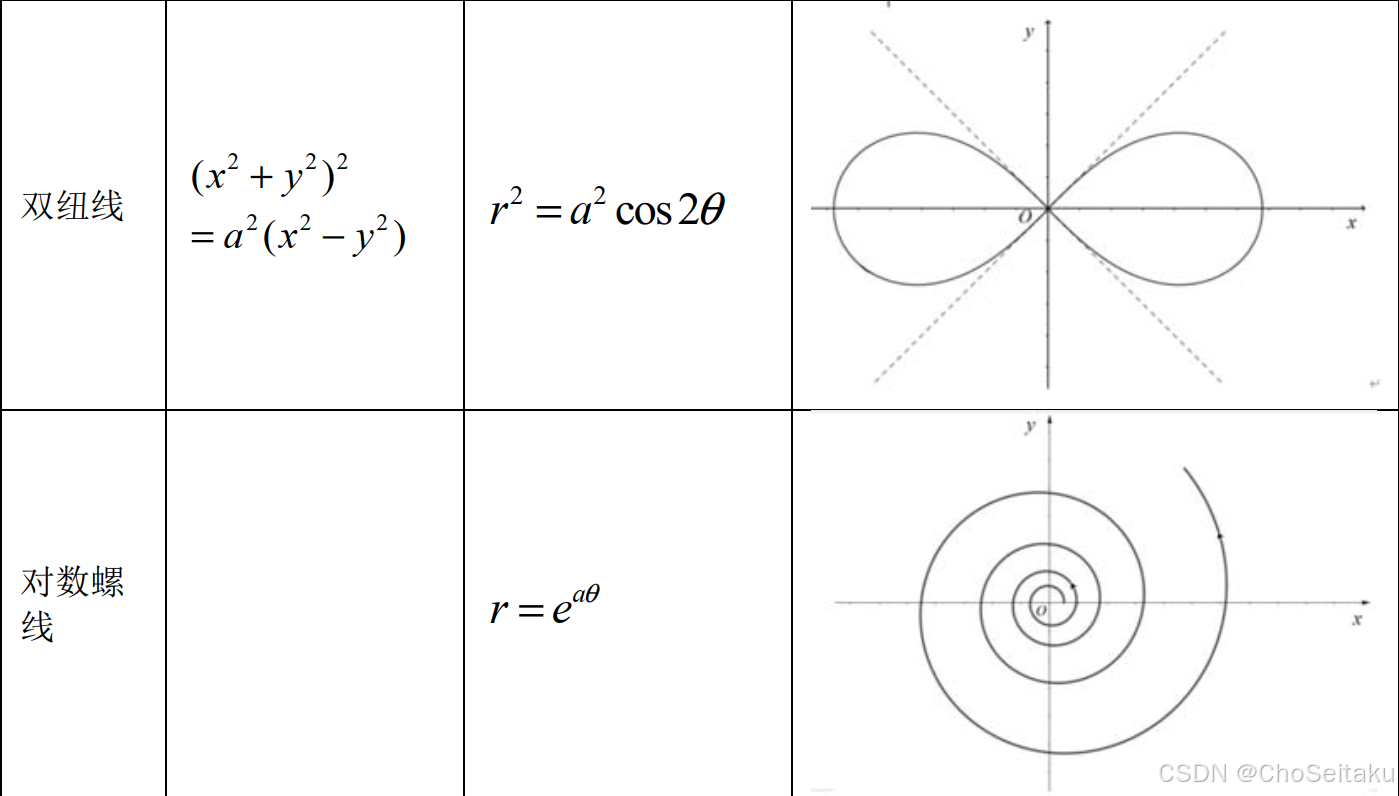
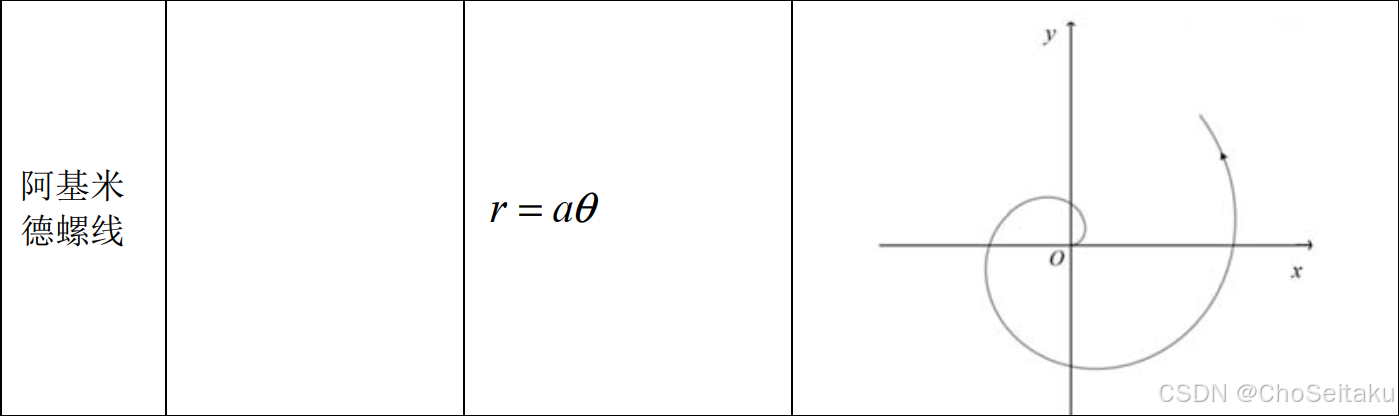
简单几何体的体积
平行截面面积已知的立体图形的体积
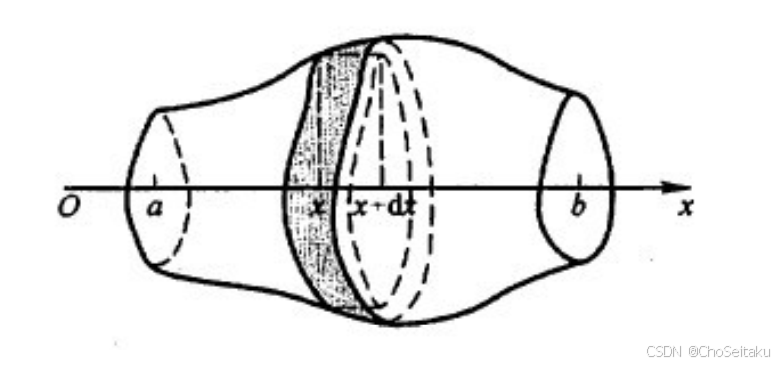
立体在过点x=a,x=b且垂直于x轴的两个平面之间,以S(x)表示过点x且垂直于x轴的截面面积.则所求立体的体积为:V=∫abS(x)dx. \begin{aligned} &\text{立体在过点}x=a,x=b\text{且垂直于}x\text{轴的两个平面之间,以}S(x)\text{表示过点}x\text{且垂直} \\ &\text{于}x\text{轴的截面面积.} \\ \\ &\text{则所求立体的体积为:}V = \int_{a}^{b} S(x)dx. \end{aligned} 立体在过点x=a,x=b且垂直于x轴的两个平面之间,以S(x)表示过点x且垂直于x轴的截面面积.则所求立体的体积为:V=∫abS(x)dx.
旋转体的体积
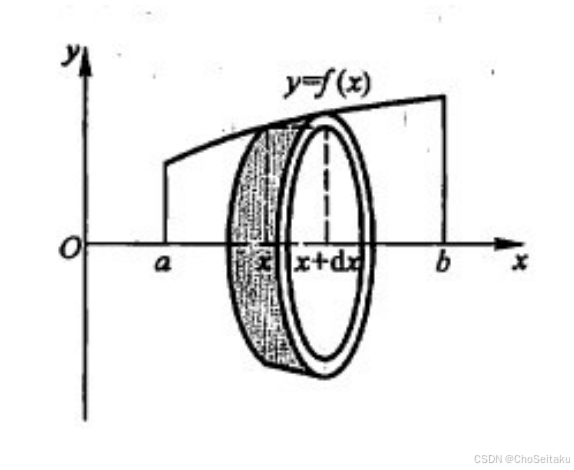
(1) 截面法:由连续曲线y=f(x),直线x=a,x=b及x轴所围曲边梯形绕x轴旋转一周而成的立体.该立体的体积为:V=∫abπf2(x)dx. \begin{aligned} &(1)\ \text{截面法:由连续曲线} y = f(x),\text{直线} x = a, x = b \text{及} x \text{轴所围曲边梯形绕} x \text{轴旋} \\ &\text{转一周而成的立体.} \\ \\ &\text{该立体的体积为:} V = \int_{a}^{b} \pi f^2(x)dx. \end{aligned} (1) 截面法:由连续曲线y=f(x),直线x=a,x=b及x轴所围曲边梯形绕x轴旋转一周而成的立体.该立体的体积为:V=∫abπf2(x)dx.
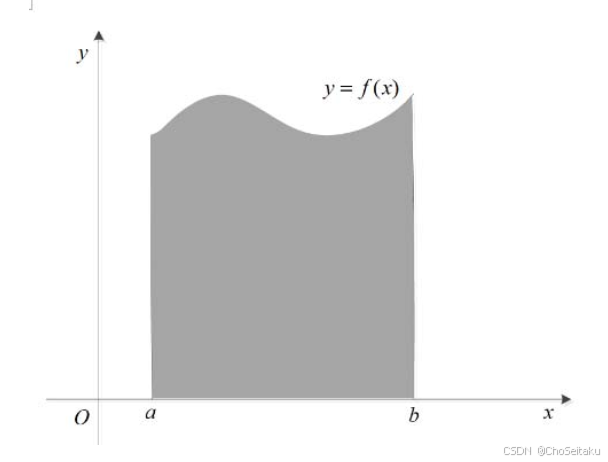
(2) 柱壳法:由曲线y=f(x),x=a,x=b (0<a<b)及x轴所围成的曲边梯形(如图)绕y轴旋转一周所得的旋转体体积计算公式为2π∫abxf(x)dx. \begin{aligned} &(2)\ \text{柱壳法:由曲线} y = f(x), x = a, x = b \ (0 < a < b) \text{及} x \text{轴所围成的曲边梯形(如} \\ &\text{图)绕} y \text{轴旋转一周所得的旋转体体积计算公式为} 2\pi\int_{a}^{b} x f(x)dx. \end{aligned} (2) 柱壳法:由曲线y=f(x),x=a,x=b (0<a<b)及x轴所围成的曲边梯形(如图)绕y轴旋转一周所得的旋转体体积计算公式为2π∫abxf(x)dx.
平面曲线的弧长
弧微分:ds=(dx)2+(dy)21. 曲线方程用参数式表示:{x=x(t)y=y(t),a≤t≤b,该曲线段的弧长为:s=∫abx′2(t)+y′2(t)dt.2. 曲线方程用显函数表示:y=f(x),a≤x≤b,该曲线段的弧长为:s=∫ab1+f′2(x)dx.3. 曲线方程用极坐标表示:r=ρ(θ),a≤θ≤b,该曲线段的弧长为:s=∫abρ2(θ)+ρ′2(θ)dθ. \begin{aligned} &\text{弧微分:}ds = \sqrt{(dx)^2 + (dy)^2} \\ \\ &1.\ \text{曲线方程用参数式表示:}\begin{cases} x = x(t) \\ y = y(t) \end{cases}, a \leq t \leq b,\text{该曲线段的弧长为:} \\ &s = \int_{a}^{b} \sqrt{x'^2(t) + y'^2(t)} dt. \\ \\ &2.\ \text{曲线方程用显函数表示:} y = f(x), a \leq x \leq b,\text{该曲线段的弧长为:} \\ &s = \int_{a}^{b} \sqrt{1 + f'^2(x)} dx. \\ \\ &3.\ \text{曲线方程用极坐标表示:} r = \rho(\theta), a \leq \theta \leq b,\text{该曲线段的弧长为:} \\ &s = \int_{a}^{b} \sqrt{\rho^2(\theta) + \rho'^2(\theta)} d\theta. \end{aligned} 弧微分:ds=(dx)2+(dy)2 1. 曲线方程用参数式表示:{x=x(t)y=y(t),a≤t≤b,该曲线段的弧长为:s=∫abx′2(t)+y′2(t) dt.2. 曲线方程用显函数表示:y=f(x),a≤x≤b,该曲线段的弧长为:s=∫ab1+f′2(x) dx.3. 曲线方程用极坐标表示:r=ρ(θ),a≤θ≤b,该曲线段的弧长为:s=∫abρ2(θ)+ρ′2(θ) dθ.
旋转曲面的面积
设在x轴上方有一条平面曲线L绕x轴旋转得到一个旋转曲面1. 若曲线方程由参数式表示:{x=x(t)y=y(t),a≤t≤b,则该旋转曲面的面积为S=2π∫aby(t)[x′(t)]2+[y′(t)]2dt.2. 若曲线方程由显函数表示:y=f(x),a≤x≤b,则该旋转曲面的面积为S=2π∫abf(x)1+[f′(x)]2dx.3. 若曲线方程由极坐标表示r=ρ(θ),a≤θ≤b,则该旋转曲面的面积为S=2π∫abρ(θ)sinθρ2(θ)+[ρ′(θ)]2dθ. \begin{aligned} &\text{设在}x\text{轴上方有一条平面曲线}L\text{绕}x\text{轴旋转得到一个旋转曲面} \\ \\ &1.\ \text{若曲线方程由参数式表示:}\begin{cases} x = x(t) \\ y = y(t) \end{cases},a \leq t \leq b,\text{则该旋转曲面的面积为} \\ &S = 2\pi\int_{a}^{b} y(t)\sqrt{[x'(t)]^2 + [y'(t)]^2} dt. \\ \\ &2.\ \text{若曲线方程由显函数表示:} y = f(x),a \leq x \leq b,\text{则该旋转曲面的面积为} \\ &S = 2\pi\int_{a}^{b} f(x)\sqrt{1 + [f'(x)]^2} dx. \\ \\ &3.\ \text{若曲线方程由极坐标表示} r = \rho(\theta),a \leq \theta \leq b,\text{则该旋转曲面的面积为} \\ &S = 2\pi\int_{a}^{b} \rho(\theta)\sin\theta\sqrt{\rho^2(\theta) + [\rho'(\theta)]^2} d\theta. \end{aligned} 设在x轴上方有一条平面曲线L绕x轴旋转得到一个旋转曲面1. 若曲线方程由参数式表示:{x=x(t)y=y(t),a≤t≤b,则该旋转曲面的面积为S=2π∫aby(t)[x′(t)]2+[y′(t)]2 dt.2. 若曲线方程由显函数表示:y=f(x),a≤x≤b,则该旋转曲面的面积为S=2π∫abf(x)1+[f′(x)]2 dx.3. 若曲线方程由极坐标表示r=ρ(θ),a≤θ≤b,则该旋转曲面的面积为S=2π∫abρ(θ)sinθρ2(θ)+[ρ′(θ)]2 dθ.
平面图形的面积
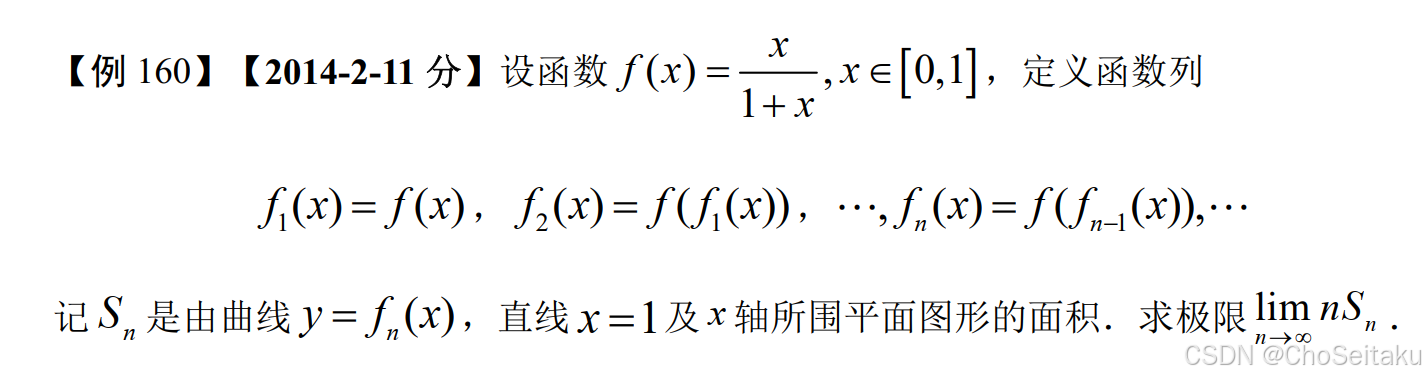
硬结合. ①fn(x),②Sn,③limn→∞nSn解:f1(x)=f(x), f2(x)=x1+x1+x1+x=x1+2x, ⋯ , fn(x)=x1+(n−1)x1+x1+(n−1)x=x1+nxSn=∫01x1+nxdx=1n∫01(1−11+nx)dx=1n(1−1nln(1+nx)∣01)=n−ln(1+n)n2limn→∞nSn=limn→∞n−ln(1+n)n=1 \begin{aligned} &\text{硬结合. ①} f_n(x), \text{②} S_n, \text{③} \lim_{n \to \infty} nS_n \\ \\ &\text{解:} f_1(x)=f(x),\ f_2(x)=\frac{\frac{x}{1+x}}{1+\frac{x}{1+x}}=\frac{x}{1+2x},\ \cdots,\ f_n(x)=\frac{\frac{x}{1+(n-1)x}}{1+\frac{x}{1+(n-1)x}}=\frac{x}{1+nx} \\ \\ &S_n = \int_{0}^{1} \frac{x}{1+nx} dx = \frac{1}{n} \int_{0}^{1} \left(1 - \frac{1}{1+nx}\right) dx = \frac{1}{n} \left(1 - \frac{1}{n}\ln(1+nx)\bigg|{0}^{1}\right) = \frac{n - \ln(1+n)}{n^2} \\ \\ &\lim{n \to \infty} nS_n = \lim_{n \to \infty} \frac{n - \ln(1+n)}{n} = 1 \end{aligned} 硬结合. ①fn(x),②Sn,③n→∞limnSn解:f1(x)=f(x), f2(x)=1+1+xx1+xx=1+2xx, ⋯, fn(x)=1+1+(n−1)xx1+(n−1)xx=1+nxxSn=∫011+nxxdx=n1∫01(1−1+nx1)dx=n1(1−n1ln(1+nx) 01)=n2n−ln(1+n)n→∞limnSn=n→∞limnn−ln(1+n)=1

已知:S=∫αβ12ρ2(θ)dθ解:法1:S=12∫−π6π6cos23θdθ=∫0π6cos23θdθ=u=3θ∫0π2cos2u⋅du3=13⋅π4=π12法2:S=∬D1dσ=∫−π6π6dθ∫0r(θ)rdr=∫−π6π612r2∣r=0r=r(θ)dθ=12∫−π6π6r2(θ)dθ =12∫−π6π6cos23θdθ=π12 \begin{aligned} &\text{已知:} S = \int_{\alpha}^{\beta} \frac{1}{2} \rho^2(\theta) d\theta \\ \\ &\text{解:法1:} S = \frac{1}{2}\int_{-\frac{\pi}{6}}^{\frac{\pi}{6}} \cos^2 3\theta d\theta = \int_{0}^{\frac{\pi}{6}} \cos^2 3\theta d\theta \xlongequal{u=3\theta} \int_{0}^{\frac{\pi}{2}} \cos^2 u \cdot \frac{du}{3} = \frac{1}{3} \cdot \frac{\pi}{4} = \frac{\pi}{12} \\ \\ &\text{法2:} S = \iint_{D} 1d\sigma = \int_{-\frac{\pi}{6}}^{\frac{\pi}{6}} d\theta \int_{0}^{r(\theta)} rdr = \int_{-\frac{\pi}{6}}^{\frac{\pi}{6}} \left. \frac{1}{2}r^2 \right|{r=0}^{r=r(\theta)} d\theta = \frac{1}{2}\int{-\frac{\pi}{6}}^{\frac{\pi}{6}} r^2(\theta) d\theta \\ &\quad\ = \frac{1}{2}\int_{-\frac{\pi}{6}}^{\frac{\pi}{6}} \cos^2 3\theta d\theta = \frac{\pi}{12} \end{aligned} 已知:S=∫αβ21ρ2(θ)dθ解:法1:S=21∫−6π6πcos23θdθ=∫06πcos23θdθu=3θ ∫02πcos2u⋅3du=31⋅4π=12π法2:S=∬D1dσ=∫−6π6πdθ∫0r(θ)rdr=∫−6π6π21r2 r=0r=r(θ)dθ=21∫−6π6πr2(θ)dθ =21∫−6π6πcos23θdθ=12π
【小结】本题极坐标方程、角度范围已知,故直接套用公式,S=∫αβ12ρ2(θ)dθ。 \begin{aligned} &\text{【小结】本题极坐标方程、角度范围已知,故直接套用公式,} S = \int_{\alpha}^{\beta} \frac{1}{2} \rho^2(\theta)d\theta。 \end{aligned} 【小结】本题极坐标方程、角度范围已知,故直接套用公式,S=∫αβ21ρ2(θ)dθ。

知识点回顾:①直→极,将x=rcosθ,y=rsinθ代入方程,解出r即可. ②极→直:出现三要素:rcosθ,rsinθ,r2.③上下限咋找?法1:几何法,画出图像,法2:代数法,r=cos2θ, 0≤θ≤2π, r>0解:极坐标方程为r=cos2θ,S=4⋅12∫0π4(cos2θ)2dθ=2∫0π4cos2θdθ选(A) \begin{aligned} &\text{知识点回顾:①直→极,将} x = r\cos\theta, y = r\sin\theta \text{代入方程,解出} r \text{即可.} \\ &\quad\quad\quad\quad\ ②\text{极→直:出现三要素:} r\cos\theta, r\sin\theta, r^2. \\ \\ &\text{③上下限咋找?} \\ &\text{法1:几何法,画出图像,} \\ &\text{法2:代数法,} r = \cos_{2}\theta,\ 0 \leq \theta \leq 2\pi,\ r > 0\\ &\text{解:极坐标方程为} r = \sqrt{\cos2\theta},S = 4 \cdot \frac{1}{2}\int_{0}^{\frac{\pi}{4}} \left(\sqrt{\cos2\theta}\right)^2 d\theta = 2\int_{0}^{\frac{\pi}{4}} \cos2\theta d\theta \\ &\text{选(A)} \end{aligned} 知识点回顾:①直→极,将x=rcosθ,y=rsinθ代入方程,解出r即可. ②极→直:出现三要素:rcosθ,rsinθ,r2.③上下限咋找?法1:几何法,画出图像,法2:代数法,r=cos2θ, 0≤θ≤2π, r>0解:极坐标方程为r=cos2θ ,S=4⋅21∫04π(cos2θ )2dθ=2∫04πcos2θdθ选(A)
【小结】1.直角坐标与极坐标相互转化关系:{x=rcosθy=rsinθ, x2+y2=r2。2.本题转化成极坐标方程后,角度范围也就是积分上下限是没有给出的,所以还要确定角度的范围:此题的图形是双纽线,直接用对称性即可。总结真题我们会发现,对于极坐标下的一些考查,如果图形复杂不常见往往会直接给出上下限,而对于一些常见图形,题干不会告诉上下限,所以这就要求考生记忆常见图形图像、性质等。 \begin{aligned} &\text{【小结】1.直角坐标与极坐标相互转化关系:}\begin{cases} x = r\cos\theta \\ y = r\sin\theta \end{cases},\ x^2 + y^2 = r^2。 \\ \\ &2.\text{本题转化成极坐标方程后,角度范围也就是积分上下限是没有给出的,所以还要确定} \\ &\text{角度的范围:此题的图形是双纽线,直接用对称性即可。} \\ \\ &\text{总结真题我们会发现,对于极坐标下的一些考查,如果图形复杂不常见往往会直接给出} \\ &\text{上下限,而对于一些常见图形,题干不会告诉上下限,所以这就要求考生记忆常见图形} \\ &\text{图像、性质等。} \end{aligned} 【小结】1.直角坐标与极坐标相互转化关系:{x=rcosθy=rsinθ, x2+y2=r2。2.本题转化成极坐标方程后,角度范围也就是积分上下限是没有给出的,所以还要确定角度的范围:此题的图形是双纽线,直接用对称性即可。总结真题我们会发现,对于极坐标下的一些考查,如果图形复杂不常见往往会直接给出上下限,而对于一些常见图形,题干不会告诉上下限,所以这就要求考生记忆常见图形图像、性质等。
简单几何体的体积
①公式回顾:S绕x轴旋转:V=∫abπf2(x)dxS绕y轴旋转:V=∫ab2πxf(x)dx②公式拓展:S绕y=−1旋转:V=∫abπ(f(x)−(−1)‾)2dx函数值到旋转轴的距离S绕x=−1旋转:V=∫ab2π(x−(−1)‾)f(x)dx,柱壳到旋转轴的距离 \begin{aligned} &\text{①公式回顾:} \\ &S\text{绕}x\text{轴旋转:} V = \int_{a}^{b} \pi f^2(x)dx \\ &S\text{绕}y\text{轴旋转:} V = \int_{a}^{b} 2\pi x f(x)dx \\ \\ &\text{②公式拓展:} \\ &S\text{绕}y=-1\text{旋转:} V = \int_{a}^{b} \pi \left( \underline{f(x)-(-1)} \right)^2 dx \quad \text{函数值到旋转轴的距离} \\ &S\text{绕}x=-1\text{旋转:} V = \int_{a}^{b} 2\pi \left( \underline{x-(-1)} \right) f(x)dx, \quad \text{柱壳到旋转轴的距离} \end{aligned} ①公式回顾:S绕x轴旋转:V=∫abπf2(x)dxS绕y轴旋转:V=∫ab2πxf(x)dx②公式拓展:S绕y=−1旋转:V=∫abπ(f(x)−(−1))2dx函数值到旋转轴的距离S绕x=−1旋转:V=∫ab2π(x−(−1))f(x)dx,柱壳到旋转轴的距离
③公式辨析:围成轴、旋转轴、自变量三因素:和横轴(竖轴)围成,绕横轴(竖轴)转,函数表达式关于x(还是y).结论:① 围成轴与旋转轴一致,用截面法,积分变量看围成轴;② 围成轴与旋转轴不一致,用柱壳法,积分变量看围成轴. \begin{aligned} &\text{③公式辨析:围成轴、旋转轴、自变量} \\ &\text{三因素:和横轴(竖轴)围成,绕横轴(竖轴)转,函数表达式关于}x\text{(还是}y\text{)}. \\ \\ &\text{结论:} \\ &①\ \text{围成轴与旋转轴一致,用截面法,积分变量看围成轴;} \\ &②\ \text{围成轴与旋转轴不一致,用柱壳法,积分变量看围成轴.} \end{aligned} ③公式辨析:围成轴、旋转轴、自变量三因素:和横轴(竖轴)围成,绕横轴(竖轴)转,函数表达式关于x(还是y).结论:① 围成轴与旋转轴一致,用截面法,积分变量看围成轴;② 围成轴与旋转轴不一致,用柱壳法,积分变量看围成轴.
③ 围成轴与旋转轴有平移,用减法;④ 自变量与围成轴不一致时,要反解. \begin{aligned} &③\ \text{围成轴与旋转轴有平移,用减法;} \\ &④\ \text{自变量与围成轴不一致时,要反解.} \end{aligned} ③ 围成轴与旋转轴有平移,用减法;④ 自变量与围成轴不一致时,要反解.
自变量与旋转轴一致
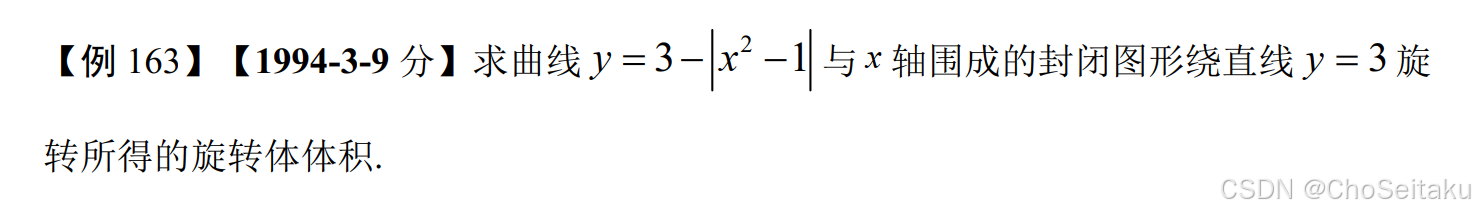
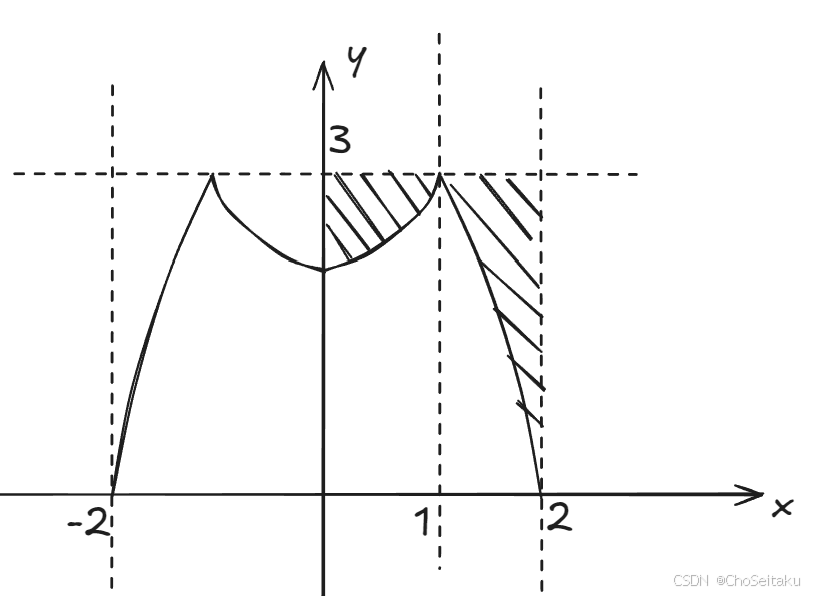
围成轴:横轴旋转轴:横轴自变量:关于x积分解:V=2(π⋅32⋅1−π∫01[(2x2)−3]2dx +π⋅32⋅1−∫12π[(4−x2)−3]2dx) =44815π \begin{aligned} &\text{围成轴:横轴} \\ &\text{旋转轴:横轴} \\ &\text{自变量:关于}x\text{积分} \\ \\ &\text{解:} V=2\left( \pi \cdot 3^2 \cdot 1 - \pi \int_{0}^{1}\left[(2x^2)-3\right]^2dx \right. \\ &\quad\quad\ \left. +\pi \cdot 3^2 \cdot 1 - \int_{1}^{2}\pi\left[(4-x^2)-3\right]^2dx \right) \\ &\quad\ = \frac{448}{15}\pi \end{aligned} 围成轴:横轴旋转轴:横轴自变量:关于x积分解:V=2(π⋅32⋅1−π∫01[(2x2)−3]2dx +π⋅32⋅1−∫12π[(4−x2)−3]2dx) =15448π
【小结】自变量与旋转轴一致的推广:当区域表示为y=f(x)时,其自变量为x,旋转轴为x轴或与x轴平行,也是自变量与旋转轴一致。当区域表示为x=g(y)时,同理。 \begin{aligned} &\text{【小结】自变量与旋转轴一致的推广:当区域表示为} y = f(x) \text{时,其自变量为} x,\text{旋转} \\ &\text{轴为} x \text{轴或与} x \text{轴平行,也是自变量与旋转轴一致。当区域表示为} x = g(y) \text{时,同理。} \end{aligned} 【小结】自变量与旋转轴一致的推广:当区域表示为y=f(x)时,其自变量为x,旋转轴为x轴或与x轴平行,也是自变量与旋转轴一致。当区域表示为x=g(y)时,同理。

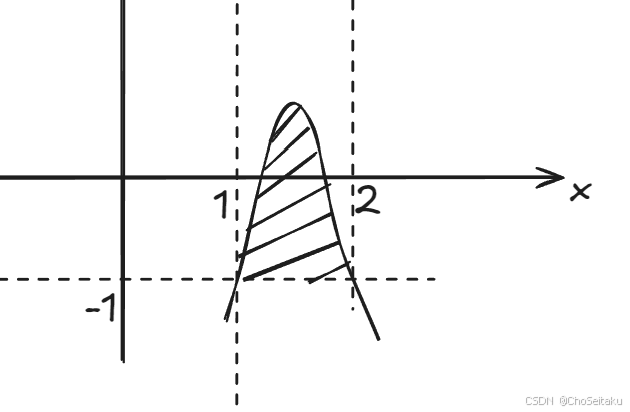
解:f(x,y)=∫∂f∂ydy=∫2(y+1)dy=(y+1)2+C(x)f(y,y)=(y+1)2+C(y)=(y+1)2−(2−y)lny,C(y)=−(2−y)lnyf(x,y)=(y+1)2−(2−x)lnx=0的方程为 (y+1)2=(2−x)lnx与y=−1的交点为(2−x)lnx=0, x=1或 x=2.V=∫12π[y−(−1)]2dx=∫12π(2−x)lnxdx=(2ln2−54)π \begin{aligned} &\text{解:} f(x,y) = \int \frac{\partial f}{\partial y} dy = \int 2(y+1)dy = (y+1)^2 + C(x) \\ \\ &f(y,y) = (y+1)^2 + C(y) = (y+1)^2 - (2-y)\ln y, \quad C(y) = -(2-y)\ln y \\ \\ &f(x,y) = (y+1)^2 - (2-x)\ln x = 0 \text{的方程为} \ (y+1)^2 = (2-x)\ln x \\ \\ &\text{与} y=-1 \text{的交点为} (2-x)\ln x = 0, \ x=1 \text{或} \ x=2. \\ \\ &V = \int_{1}^{2} \pi \left[y - (-1)\right]^2 dx = \int_{1}^{2} \pi (2-x)\ln x dx = \left(2\ln2 - \frac{5}{4}\right)\pi \end{aligned} 解:f(x,y)=∫∂y∂fdy=∫2(y+1)dy=(y+1)2+C(x)f(y,y)=(y+1)2+C(y)=(y+1)2−(2−y)lny,C(y)=−(2−y)lnyf(x,y)=(y+1)2−(2−x)lnx=0的方程为 (y+1)2=(2−x)lnx与y=−1的交点为(2−x)lnx=0, x=1或 x=2.V=∫12π[y−(−1)]2dx=∫12π(2−x)lnxdx=(2ln2−45)π
【小结】旋转体的体积,关键就是找到截面面积(方法是垂直于旋转轴做截面),然后对截面面积积分即可。 \begin{aligned} &\text{【小结】旋转体的体积,关键就是找到截面面积(方法是垂直于旋转轴做截面),然后对} \\ &\text{截面面积积分即可。} \end{aligned} 【小结】旋转体的体积,关键就是找到截面面积(方法是垂直于旋转轴做截面),然后对截面面积积分即可。
自变量与旋转轴垂直

解:{2f(x)+x2f(1x)=x2+2x1+x22f(1x)+1x2f(x)=1x2+2x1+1x2=1+2xx1+x2整理得:{4f(x)+2x2f(1x)=2x2+4x1+x2①2x2f(1x)+f(x)=x+2x21+x2②①−②,得:f(x)=x1+x2 \begin{aligned} &\text{解:} \begin{cases} 2f(x) + x^2f\left(\frac{1}{x}\right) = \frac{x^2 + 2x}{\sqrt{1+x^2}} \\ 2f\left(\frac{1}{x}\right) + \frac{1}{x^2}f(x) = \frac{\frac{1}{x^2} + \frac{2}{x}}{\sqrt{1+\frac{1}{x^2}}} = \frac{1 + 2x}{x\sqrt{1+x^2}} \end{cases} \\ \\ &\text{整理得:} \begin{cases} 4f(x) + 2x^2f\left(\frac{1}{x}\right) = \frac{2x^2 + 4x}{\sqrt{1+x^2}} \quad ① \\ 2x^2f\left(\frac{1}{x}\right) + f(x) = \frac{x + 2x^2}{\sqrt{1+x^2}} \quad ② \end{cases} \\ \\ &① - ② \text{,得:} f(x) = \frac{x}{\sqrt{1+x^2}} \end{aligned} 解:⎩ ⎨ ⎧2f(x)+x2f(x1)=1+x2 x2+2x2f(x1)+x21f(x)=1+x21 x21+x2=x1+x2 1+2x整理得:{4f(x)+2x2f(x1)=1+x2 2x2+4x①2x2f(x1)+f(x)=1+x2 x+2x2②①−②,得:f(x)=1+x2 x
x=y21−y2 x = \sqrt{\frac{y^2}{1 - y^2}} x=1−y2y2
围成轴:竖轴旋转轴:横轴自变量:yV=∫12322πy⋅y21−y2dy=π26 \begin{aligned} &\text{围成轴:竖轴} \\ &\text{旋转轴:横轴} \\ &\text{自变量:} y \\ \\ &V = \int_{\frac{1}{2}}^{\frac{\sqrt{3}}{2}} 2\pi y \cdot \sqrt{\frac{y^2}{1-y^2}} dy = \frac{\pi^2}{6} \end{aligned} 围成轴:竖轴旋转轴:横轴自变量:yV=∫2123 2πy⋅1−y2y2 dy=6π2
【小结】1.本题可以解释自变量与旋转轴垂直的意思是:当区域表示为y=f(x)时,其自变量为x,旋转轴为y轴或与y轴平行,即自变量与旋转轴垂直。当区域表示为x=g(y)时,同理。2.自变量与旋转轴垂直,可以转化成自变量与旋转轴一致的问题解决,如本题区域是y=f(x)时,旋转轴与y轴平行,可以写为x=g(y),旋转轴与y轴平行,自变量与旋转轴一致,用截面法。 \begin{aligned} &\text{【小结】1.本题可以解释自变量与旋转轴垂直的意思是:} \\ &\text{当区域表示为} y = f(x) \text{时,其自变量为} x,\text{旋转轴为} y \text{轴或与} y \text{轴平行,即自变量与} \\ &\text{旋转轴垂直。当区域表示为} x = g(y) \text{时,同理。} \\ \\ &2.\text{自变量与旋转轴垂直,可以转化成自变量与旋转轴一致的问题解决,如本题区域是} \\ &y = f(x) \text{时,旋转轴与} y \text{轴平行,可以写为} x = g(y),\text{旋转轴与} y \text{轴平行,自变量与} \\ &\text{旋转轴一致,用截面法。} \end{aligned} 【小结】1.本题可以解释自变量与旋转轴垂直的意思是:当区域表示为y=f(x)时,其自变量为x,旋转轴为y轴或与y轴平行,即自变量与旋转轴垂直。当区域表示为x=g(y)时,同理。2.自变量与旋转轴垂直,可以转化成自变量与旋转轴一致的问题解决,如本题区域是y=f(x)时,旋转轴与y轴平行,可以写为x=g(y),旋转轴与y轴平行,自变量与旋转轴一致,用截面法。