注:博主并非旨在对针对文章中提及论文的实验设计、数据及结果进行逐一还原,而是针对其核心方法论或关键创新点,通过自行设计的实验流程进行验证与探索。若是完整的论文复现,会进行提前说明。
1 论文简介
《Robust Image Segmentation Using FCM With Spatial Constraints Based on New Kernel-Induced Distance Measure》是由 Songcan Chen 和 Daoqiang Zhang 于 2004 年发表在《IEEE Transactions on Systems, Man, and Cybernetics, Part B》期刊上的一篇论文。该论文针对传统模糊 C 均值聚类算法及其带有空间约束的变体在图像分割中存在的两个关键问题------对噪声和离群点敏感,以及无法有效处理数据中非欧几里得结构------提出了一种创新的解决方案。核心方法是利用核方法,将原始数据隐式映射到高维特征空间,并基于此诱导出一类新的、鲁棒的非欧几里得距离度量,进而将原有的 FCM_S 系列算法扩展为对应的核化版本,即 KFCM_S、KFCM_S1 和 KFCM_S2。这种方法不仅通过核函数(如高斯 RBF 核)的固有特性增强了算法对噪声和异常值的鲁棒性,还能更好地揭示数据中复杂的非线性聚类结构,同时通过特定的设计保持了类中心在原数据空间的可解释性,从而在计算复杂度和直观理解之间取得了良好平衡。该方法因其出色的鲁棒性和对复杂数据的适应性,被广泛应用于医学影像分析(如 MRI 脑部图像分割)和受噪声污染的合成及真实图像的分割任务中,对后续结合核技术与空间上下文的图像分割研究产生了重要影响。
2 FCM_S2 算法原理
FCM_S2 是模糊 C 均值空间约束算法的另一个低复杂度变体,其核心思想与 FCM_S1 相似,旨在通过简化邻域计算来提高效率。两者的主要区别在于:FCM_S1 使用邻域像素的均值向量来代表空间上下文,而 FCM_S2 则使用邻域像素的中值向量。这种改变使 FCM_S2 对"椒盐"噪声等离群点具有更强的鲁棒性,因为中值滤波能更好地抑制这类极端噪声值。
假设待分割图像有 NNN 个像素,每个像素 xk\mathbf{x}_kxk 是一个 ddd 维特征向量,目标是将像素划分到 ccc 个聚类中。 x~k\tilde{\mathbf{x}}_kx~k 表示以像素 xk\mathbf{x}_kxk 为中心的指定窗口(如 3×33 \times 33×3 )内所有邻域像素特征向量的中值向量,该值可预先计算并存储。
步骤 1:算法初始化
固定聚类数目 ccc ,初始化 ccc 个聚类中心 vi\mathbf{v}_ivi (i=1,...,c)(i=1,...,c)(i=1,...,c) ,设定阈值 ε>0\varepsilon > 0ε>0 、模糊权重指数 mmm (通常 m=2m=2m=2 )和空间约束权重参数 α\alphaα 。
步骤 2:计算中值滤波图像
在迭代开始前,对整幅图像进行中值滤波,为每个像素 xk\mathbf{x}_kxk 计算出其对应的邻域中值向量 x~k\tilde{\mathbf{x}}_kx~k 。
步骤 3:迭代更新隶属度矩阵 UUU
在每次迭代中,根据当前聚类中心 vi\mathbf{v}_ivi ,按下式计算每个像素 xk\mathbf{x}kxk 属于第 iii 个聚类的隶属度 uiku{ik}uik :
uik=(∣xk−vi∣2+α∣x~k−vi∣2)−1(m−1)∑j=1c(∣xk−vj∣2+α∣x~k−vj∣2)−1(m−1) u_{ik} = \frac{ \left( |\mathbf{x}_k - \mathbf{v}_i|^2 + \alpha |\tilde{\mathbf{x}}_k - \mathbf{v}i|^2 \right)^{ -\frac{1}{(m-1)} } }{ \sum{j=1}^{c} \left( |\mathbf{x}_k - \mathbf{v}_j|^2 + \alpha |\tilde{\mathbf{x}}_k - \mathbf{v}_j|^2 \right)^{ -\frac{1}{(m-1)} } } uik=∑j=1c(∣xk−vj∣2+α∣x~k−vj∣2)−(m−1)1(∣xk−vi∣2+α∣x~k−vi∣2)−(m−1)1
该公式与 FCM_S1 形式完全相同,但将均值向量 x‾k\overline{\mathbf{x}}_kxk 替换为了中值向量 x~k\tilde{\mathbf{x}}_kx~k 。距离项 ∣x~k−vi∣2|\tilde{\mathbf{x}}_k - \mathbf{v}_i|^2∣x~k−vi∣2 利用中值向量引入空间连续性约束, α\alphaα 控制其权重。
步骤 4:迭代更新聚类中心 vi\mathbf{v}_ivi
根据更新后的隶属度 uiku_{ik}uik ,按下式重新计算每个聚类中心 vi\mathbf{v}_ivi :
vi=∑k=1Nuikm(xk+αx~k)(1+α)∑k=1Nuikm \mathbf{v}i = \frac{ \sum{k=1}^{N} u_{ik}^{m} ( \mathbf{x}k + \alpha \tilde{\mathbf{x}}k ) }{ (1 + \alpha) \sum{k=1}^{N} u{ik}^{m} } vi=(1+α)∑k=1Nuikm∑k=1Nuikm(xk+αx~k)
新的聚类中心是原始像素和其邻域中值向量的加权平均。由于中值向量 x~k\tilde{\mathbf{x}}_kx~k 对离群点不敏感,因此由此更新得到的聚类中心也更具鲁棒性。
步骤 5:检查收敛条件
重复步骤 3 和步骤 4,直到目标函数的变化量小于预设阈值 ε\varepsilonε。此时算法收敛,得到最终的模糊分割结果。
3 实验结果
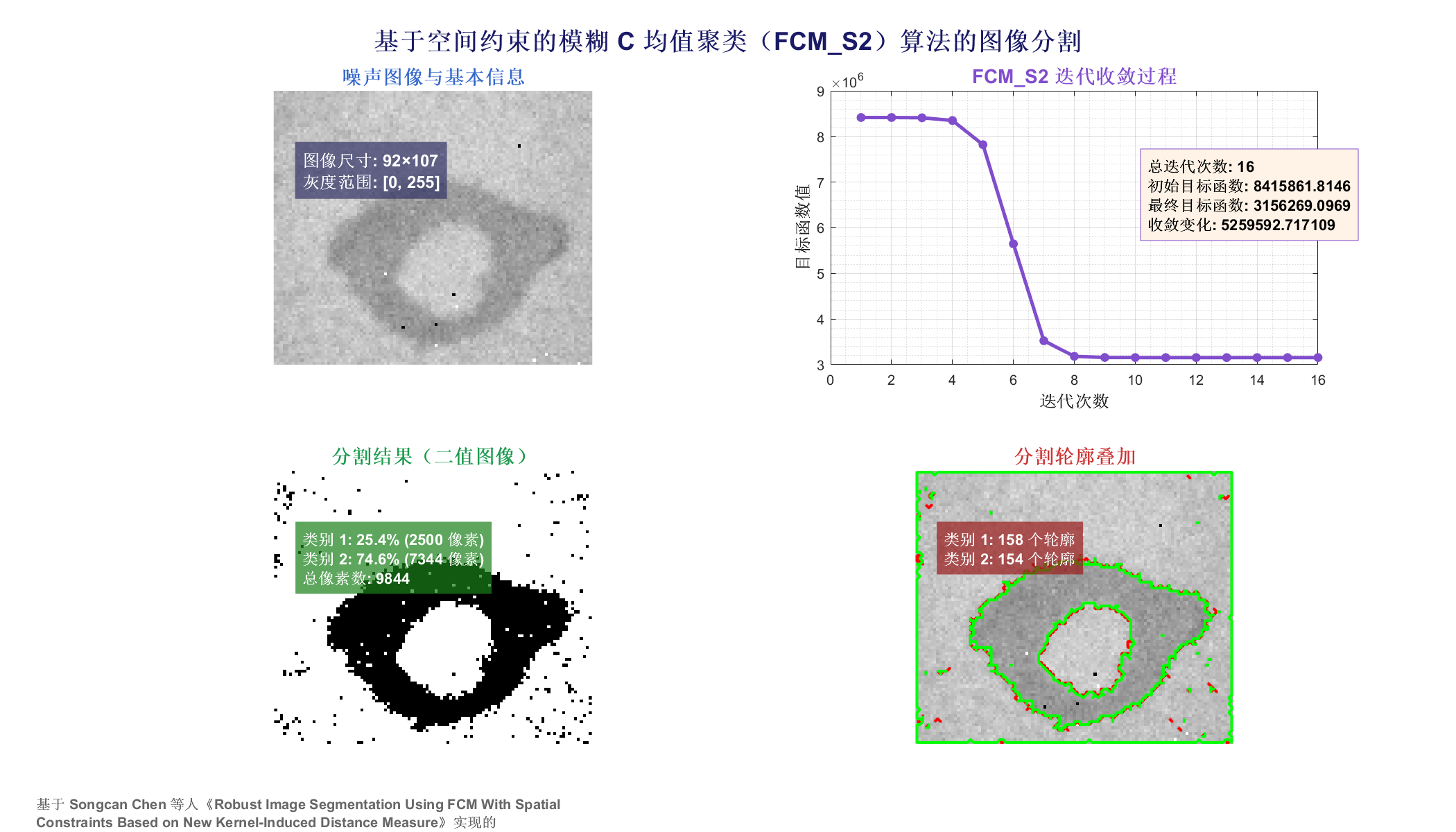
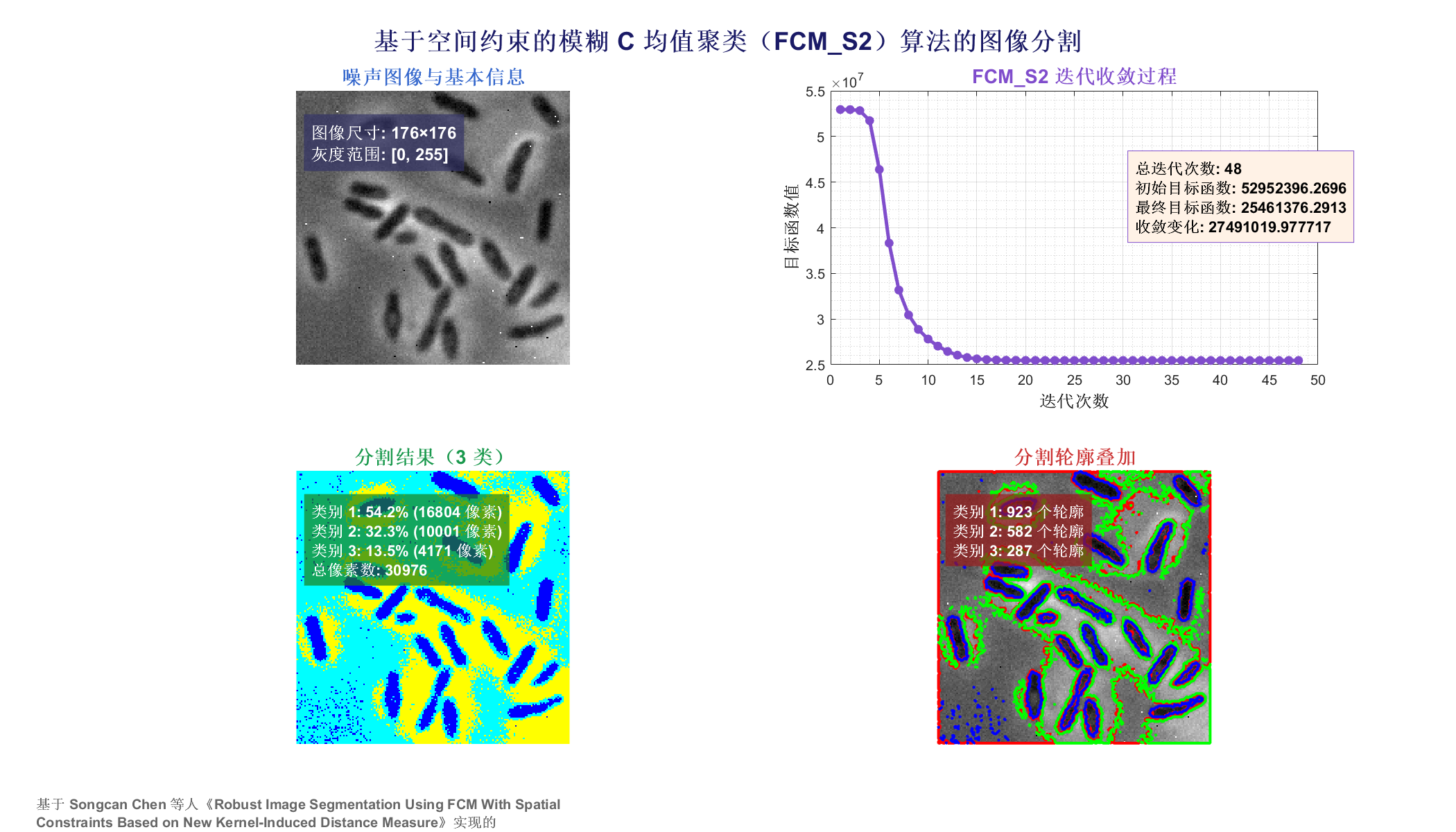
4 参考文献
1\] Chen, Songcan, and Daoqiang Zhang. "Robust image segmentation using FCM with spatial constraints based on new kernel-induced distance measure." IEEE Transactions on Systems, Man, and Cybernetics, Part B (Cybernetics) 34.4 (2004): 1907-1916. ## 5 MATLAB 代码